Похожие презентации:
Алгебра және анализ бастамалары
1.
10 сыныпАлгебра және анализ бастамалары
Умбетова Меруерт Мирзамидиновна
2.
КөпмүшелерБірнеше айнымалысы бар
көпмүшенің түрі
және сипаттамасы.
Анықтама. Бірмүшелердің қосындысы көпмүше деп
аталады
Анықтама. Көпмүшенің құрамына кіретін бірмүшелер
көпмүшенің мүшелері д.а.
Бірнеше айнымалы көпмүше n-ші дәрежелі біртектi
көпмүше деп аталады, егер көпмүшенің әрбір мүшесінің
дәреже көрсеткіштерінің қосындысы n-ге тең болса.
Умбетова Меруерт Мирзамидиновна
3.
4.
Өрнектерді қарап шығыңыз. Бір айнымалы көпмүшелердіңқасына «˅» белгісін, бірнеше айнымалы көпмүше қасына
«+» белгісін, көпмүше болып табылмайтын өрнектер қасына
«–» белгісін қойыңыздар.
a)2 x x 3x 2 x 5
5
4
3
2
b)2 x x 3
g )2 x 2 5xy 2 y 2
3
с) x 4 xy 5 y
3
2
3
d )16 y 7 72 y 6 108 y 5 54 y 4
e)3ab
2
2
f ) x 2
x
h)t t 3t
3
k ) x 4x
3
5
3
l ) x 3 3x 2 5 х 15
5.
a)2 x x 3x 2 x 5 ˅5
4
3
2
b)2 x x 3 ˅
g )2 x 5xy 2 y
2
2 _
3
с) x 4 xy 5 y +
3
2
h)t t 3t ˅
3
3
d )16 y 7 72 y 6 108 y 5 54 y 4 ˅
k)x 4x
3
5
3
˅
l ) x 3 3x 2 5 х 15
_
e)3ab +
2
f ) x 2
x
2
˅
Умбетова Меруерт Мирзамидиновна
6.
Көпмүшенің анықтамасы!!! Дәреже көрсеткіштері теріс емес бүтін сан болу керек
7.
Умбетова Меруерт Мирзамидиновна8.
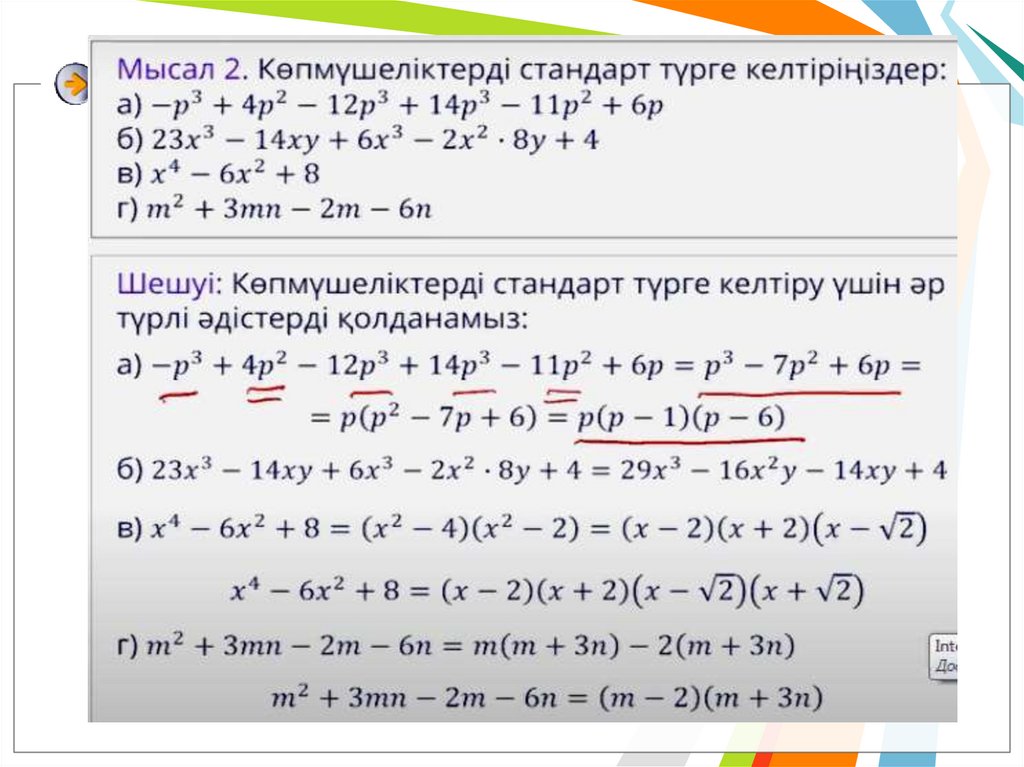
Тапсырма№1.көпмүшені канондық түрде жазыңыз
а) (х + 1)(х - 1)(х - 2);
б)
(х + 1)2(х - 2) - (х + 1)(х - 2)2,
в)
(2х + 1)(2х - I)2;
г)
(2х + 1)(2х - I)2 + (1 - 2х)3
9.
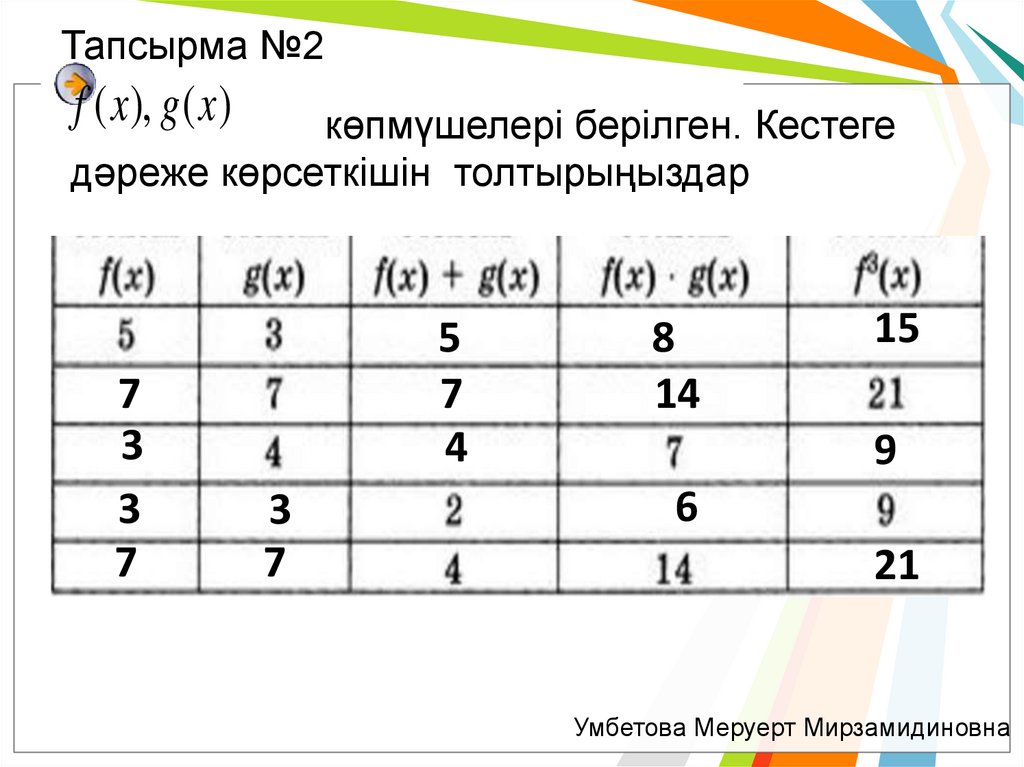
Тапсырма №2f ( x ), g ( x )
көпмүшелері берілген. Кестеге
дәреже көрсеткішін толтырыңыздар
7
3
3
7
5
7
4
3
7
8
14
15
9
6
21
Умбетова Меруерт Мирзамидиновна
10.
Көпмүшені стандарт түрде жазыңыза) (2х-у-3)2+(х-Зу-1)2;
б)
(х - у - 2z - 1)2 + (2х+ у + z - З)2;
в)
(5х - у - 2)2 + 2(3х - у -1)2;
г)
(х - Зу + z - 2)2 - 3(2х + у - z + 1).
11.
Тақырып:Біртекті және
симметриялы көпмүшелер
Умбетова Меруерт Мирзамидиновна
12.
Жаңа материал бойынша теориялық түсінікберу
Анықтама: Көпмүшенің әрбір бірмүшелерінің
дәрежелері тең болса, онда мұндай көпмүше
біртекті көпмүше деп аталады.
Мысалы: х + 3у, xy(x+y)
көпмүшелері біртекті көпмүшер болады.
Анықтама: Егер f (x;y) көпмүшесіндегі х-ті у-ке,
ал у-ті х-ке ауыстырғанда, берілген көпмүше
өзгермесе, ондай көпмүше симметриялы
көпмүше деп аталады.
Ең қарапайым симметриялы көпмүшелер: х + у
және ху. Бұл көпмүшелерді элементар
көпмүшелер деп айтады
13.
Умбетова Меруерт Мирзамидиновна14.
Умбетова Меруерт Мирзамидиновна15.
Умбетова Меруерт Мирзамидиновна16.
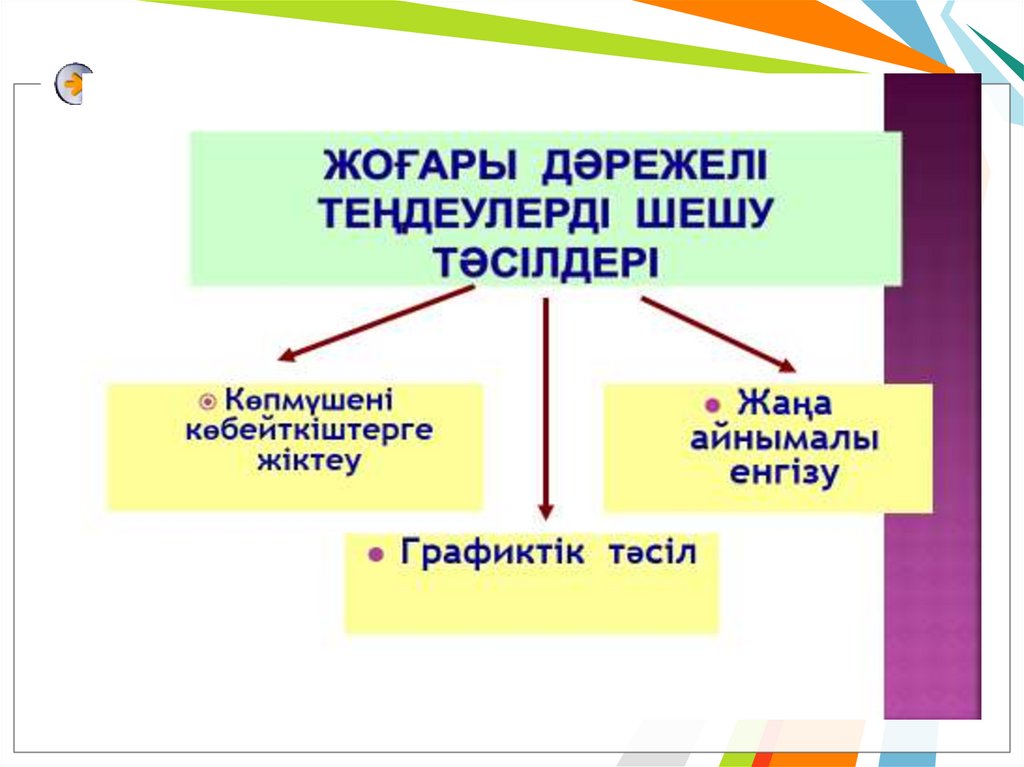
Тақырып:Көбейткіштерге жіктеу әдісі
арқылы бір айнымалысы бар
көпмүше түбірлерін табу
Умбетова Меруерт Мирзамидиновна
17.
18.
19.
20.
Мысал:21.
22.
Кубтық теңдеулердішешу алгоритімі:
• Ax3+Bx2+Cx+D=0 түріндегі кубтық теңдеуді
шешудің алгоритімін қарастырамыз, мұнда
x=0 сол теңдеудің шешімі болатын болса
• Бұл жағдайда D бос мүшесі нөлге тең болса
онда теңдеу келесі түрге айналады
Ax3+Bx2+Сx=0
• осы теңдеуден х айнымалысын жақша
сыртына шығарсақ бір түбірі 0-ге тең. ал жақша
ішіндегі теңдеудің түбірлерін Виетпен немесе
Дискриминатпен есептеп шығамыз
x(Ax2+Bx+C)=0
23.
Мысалдарқарасытрамыз:
Теңдеуді шеш: 3x3+4x2+2x=0
Шешуі:
3x3+4x2+2x=0
x(3x2+4x+2)=0
x=0 бір түбірі.
Енді квадрат үшмүшенің түбірін табамыз:
3x2+4x+2
D=42-4*3*2=-8 дискриминан нөлден кіші
болса түбірі жоқ
24.
Биквадрат теңдеудішешу алгоритімі:
• ax4 + bx2 + c = 0 теңдеуі биквадрат
теңдеу д.а.
• Жаңа айнымалы енгіземіз:y=x2 онда
теңдеу келесі түрде жазылады:
y2+by+c=0.
• Енді бұрынғыша кварат теңдеуді
шешеміз
• Табылған түбірлерді у жаа
айнымалысының орнына қоямыз
Умбетова Меруерт Мирзамидиновна
25.
Мысал:теңдеуді шеш: x4 - 10x2 + 1 = 0 .
Шешуі:
y1,2=5 ± √(24).
Теңдеуді шешсек түбірлері
x2 =5+ √(24)
және x2 =- √(24)
Жауабы::X1,2,3,4=± √(5 ± √(24)).
y= x2, y2-10y+1=0,онда
Умбетова Меруерт Мирзамидиновна
26.
Бір айнымалысы бар көпмүшер(x) = anxn + an-1xn-1 +…+ a3x3 + a2x2 + a1x + ao
- р(х) көпмүшенің стандарт түрі
anxn –р(х) көпмүшесініңең ең үлкен мүшесі
an – ең үлкен мүшесінің коэффициенті
n – көпмүшенің дәрежесі
aо –р(х) көпмүшесінің бос мүшесі
Егер an = 1 болса, ондар(х) көпмүшесі
келтірілген деп аталады
егер an ≠ 1, р(х) көпмүшесі келтірілмеген
көпмүше деп аталады
27.
Көпмүшелерді бөлуp(x) көпмүшесі s(x) көпмүшесіне бөлінеді деп
айтамыз, егер сәйкестік орындалатындай
q(x) көпмүшесі бар болса.
р(x) = s(x) q(x)
p(x) – бөлінді
s(x) – бөлгіш
q(x) – бөлінгіш
Умбетова Меруерт Мирзамидиновна
28.
Көпмүшелерді бөлу1 мысал
х3 − 3х2 + 5х − 15 = (х2 + 5)(х − 3) болса,
онда х3 − 3х2 + 5х − 15 көпмүшесі х2 + 5
және х − 3 көпмүшелеріне бөлінеді
бөлінгіш
бөлгіш
х3 − 3х2 + 5х − 15
− 3
х
+ 5х
− 3х2
− 15
−
− 3х2
− 15
0
х2 + 5
х −3
бөлінді
Умбетова Меруерт Мирзамидиновна
29.
• Жаңа материал бойынша теориялықтүсінік беру
• Көпмүшелерді қалдықпен бөлу үшін «бұрыштап
бөлу» тәсілі қолданылады.
• Кез келген f(x)және g(x) көпмүшелері үшін q(x) және
r(x) көпмүшелері табылып,
• f(x)=g(x)*q(x)+r(x) теңдігі орындалады.
• Мұнда r(x) -тің дәрежесі g(x) -тің дәрежесінен кіші
немесе r(x)=0 болады. g(x) көпмүшесі f(x)-ті
g(x)көпмүшесіне бөлгендегі толымсыз бөлінді деп
айтады.
30.
Көпмүшелерді қалдықпен бөлур(x) = s(x) q(x) + r(х)
p(x) – көпмүше
s(x) – бөлгіш
q(x) – толымсз бөлінді
r(x) – қалдық
31.
Қалдықпен бөлу2-Мысал
2х2 − х − 3 = 2х2 − 4х + 3х − 6 + 3 =
= 2х(х − 2) + 3(х − 2) + 3 = (х − 2)(2х + 3) + 3,
онда 2х2 − х − 3 = (х − 2)(2х + 3) +
3
бөлінгіш
бөлгіш
2х2 − х − 3
−
2х2 − 4х
3х − 3
−
3х − 6
3
х−2
2х + 3
бөлінді
қалдық
32.
33.
Безу Теоремасыкез-келген көпмүшені x − а ексімүшесіне
бөлгенде шыққан қалдық р(х) бөлінгіш
көпмүшенің х = а болғндағы мәніне тең
р(x) = (x − а) q(x) + r
p(x) –бөлінгіш
x − а –бөлгіш
q(x) – бөлінді
r – қалдық
34.
Қалдықпен бөлумысал
р(х) = 2х2 − х − 3 көпмүшесін х − 2.ге
бөлгендегі қалдықты тап
Безу теоремасы бойынша
р(2)= 2 22 − 2 − 3 = 3
2х2 − х − 3
−
2х2 − 4х
3х − 3
−
3х − 6
3
х−2
2х + 3
қалдық
35.
Горнер схемасыр(x) = bx4 + cx3 + dx2 + ex + f көпмүшесі болсын.
р(х) –ті (x − а)-ке бөліп, р(x) = (х − а )q(x) + r аламыз.
q(x) = kx3 + mx2 + nx + s, коэффициенттері Горнер
схемасы бойынша есептеледі
k=b
m = ka + c
n = ma + d
s = na + e
r = sa + f
b
a
c
d
e
k = b m = ka + c n = ma + d s = na + e
f
r = sa + f
36.
мысалыр(x) = 2x5 + x4 − 3x3 + 2x2 + 5 көпмүшесін x + 2-ге
бөлеміз.
мұнда a = − 2; Коэффициенттер сәйкесінше
2, 1, −3, 2, 0, 5 тең
Горнер схемасымен таблица құрайық:
2
1
−3
2
0
5
−2 2 2 (−2)+1 −3 (−2)+(−3) 3 (−2)+2 −4 (−2)+0 8 (−2)+5
3
2
8
−3
−4
−11
Бөлінгіштің коэффициенттері: 2, − 3, 3, − 4, 8,
Ал қалдық r = − 11.
демек, 2x5 + x4 − 3x3 + 2x2 + 5 =
= (х + 2)(2x4 − 3x3 + 3x2 − 4x + 8) − 11
қалдық
37.
Көпмүшені көпмүшеге бөлу1
2
3
4
38.
:Ортақ көбейткшті жақша сыртына
шығару
(a + b)c = ac + bc
Кері ретпен:
ac + bc = c(a + b)
4 мысал
8х4 + 6х3 − 4х2 + 2х = 2х (4х3 + 3х2 − 2х + 1)
3х3 + 6х6 − 27х4 = 3x3 (1 + 2х3 − 9x)
39.
Топтастыру әдісіҚосудың
ауыстырымды
немесе
терімділік
заңдарын
қолдану
арқылы
көпмүшенің
мүшелерін кез келген жолмен топтастыруға
болады. :
a+b=b+a
(a + b) + c = a + (b + c) = а + b + c
5 мысал
3х3 + 6х2 − 27х − 54 = 3(х3 + 2х2 − 9х − 18) =
= 3(х2 (х + 2) − 9(х + 2)) = 3(х + 2)(х2 − 9) =
= 3(х + 2)(х − 3)(х + 3)
40.
Қ.К.Ф. қолдану(a + b)(а − b) = a2 − b2
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b)(a2 − ab + b2) = а3 + b3
(a − b)(a2 + ab + b2) = а3 − b3
(a − b)3 = a3 − 3ab2 + 3a2b − b3
(a + b)3 = a3 + 3ab2 + 3a2b + b3
6 мысал
х6 − 1 = (х3)2 − 12 = (х3 + 1)(х3 − 1) =
= (х + 1)(х2 − х + 1)(х − 1)(х2 + х + 1)
41.
Квадрат үшмүшені көбейткішке жіктеуегер х1 және х2 түбірлері aх2 + bх + с
квадрат үшмүше түбірлері болса, онда
aх2 + bх + с = а (х − х1)(х − х2)
7 мысал
2х2 − 3х − 5 = 2 (х + 1)(х − 2,5) = (х + 1)(2х − 5)
42.
ТеоремаЕгер а бүтін саны бүтін коэффициентті көпмүшенің
түбірі болса, онда көпмүшенің бос мүшесі а санына
бөлінеді
43.
8 мысалКөпмүшені көбейткішке жіктеу
х3 − 3х2 − 10х + 24
Бос мүшенің бөлгіштерін іздейміз 24: ± 1; ± 2; ± 3; ± 4;
± 6; ± 8; ± 12; ± 24.
р(1) = 12 ≠ 0, р(−1) = 30 ≠ 0, р(2) = 0.
демек х = 2 –р(х) көпмүшесінің түбірі. Горнер
схемасы бойынша q(x) ті іздейміз:
2
1
1
1
−3
2 1+(−3)
−1
−10
2 (−1)−10
−12
24
2 (−12)+24
0
х3 − 3х2 − 10х + 24 = (х – 2)(х2 − х − 12) =
= (х – 2)(х − 4)(х + 3)
44.
х2 – у2 = (х – у)(х + у)х3 – у3 = (х – у)(х2 + ху + у2)
x4 – у4 = (x – y)(x3 + x2у + xy2 + уЗ)
x5 – у5 = (x – y)(х4 + хзy + х2y2 + хy3 + y4)
…
xn – уn = (x – y)(хn−1 + хn−2y + хn−3y2 + … +
+ х2yn−3 + xyn−2 + yn−1)
45.
Бірнеше айнымалысы бар көпмүшех3 + у3 = (х + у)(х2 – ху + у2)
x5 + у5 = (x + y)(х4 – х3y + х2y2 – хy3 + y4)
…
x2n+1 + у2n+1 = (x + y)(х2n – х2n−1y + х2n−2y2 –
– х2n−3y3 + … + x2y2n−2 – xy2n−1 + y2n)
46.
Жоғары дәрежелі теңдеулерТеорема.
Егер
бүтін
коэффициенттері
бар
келтірілген теңдеудің рационал түбірі болса, онда бұл
түбір міндетті түрде бүтін сан болады..
Мысал 9
х3 + 2х2 – 7х – 12 = 0
Бос мүшенің бөлгіштері12: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ±
12.
Р(х) = х3 + 2х2 – 7х – 12 болсын, онда
Р(1) = −16, Р(−1) = −4, Р(2) = −10, Р(−2) = 2, Р(3) = 12,
Р(−3) = 0.
демек х = −3 –Р(х) көпмүшесінің түірі.








































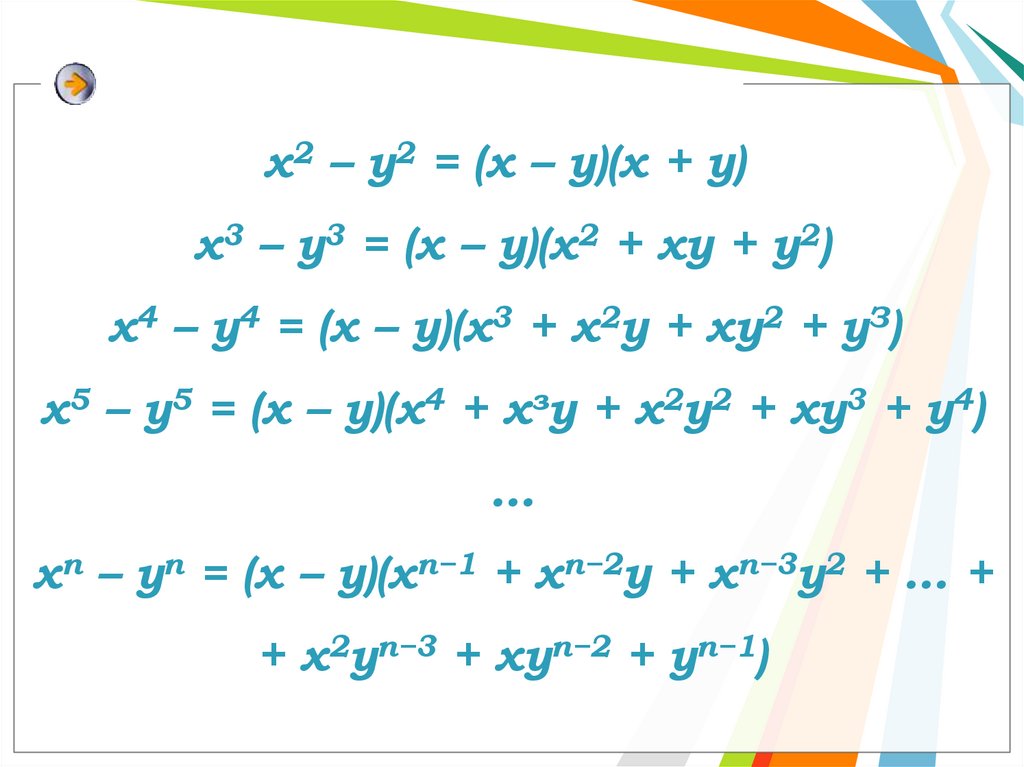



 Математика
Математика








