Микромагнитное моделирование

1.

Микромагнитное
моделирование.
Лекция 2.
Самардак
сотрудник
Алексей
Юрьевич,
Младший
научный
Лаборатории плёночных технологий, ИНТПМ ДВФУ
2021

2.

MuMax3
mumax.github.io
Расчёт на ГПУ с использованием CUDA
методом конечных разностей, может
быть установлена на любую систему с
дискретной видеокартой от Nvidia
поддерживающей
CUDA:
https://mumax.github.io/download.ht
ml
Достоинства:
• Веб-интерфейс
• Простая постановка задачи через
примитивы и логические операции
• Большое коммьюнити
• Является наследником OOMMF, делит
сdesign
ним
софт ofдля
визуализации
и
"The
and verification
mumax3",
AIP Advances 4,
107133
(2014).
обработки
полученных данных
Недостатки
• Сложность построения
нетривиальных 3Дструктур из примитивов
• Метод конечных
разностей

3.

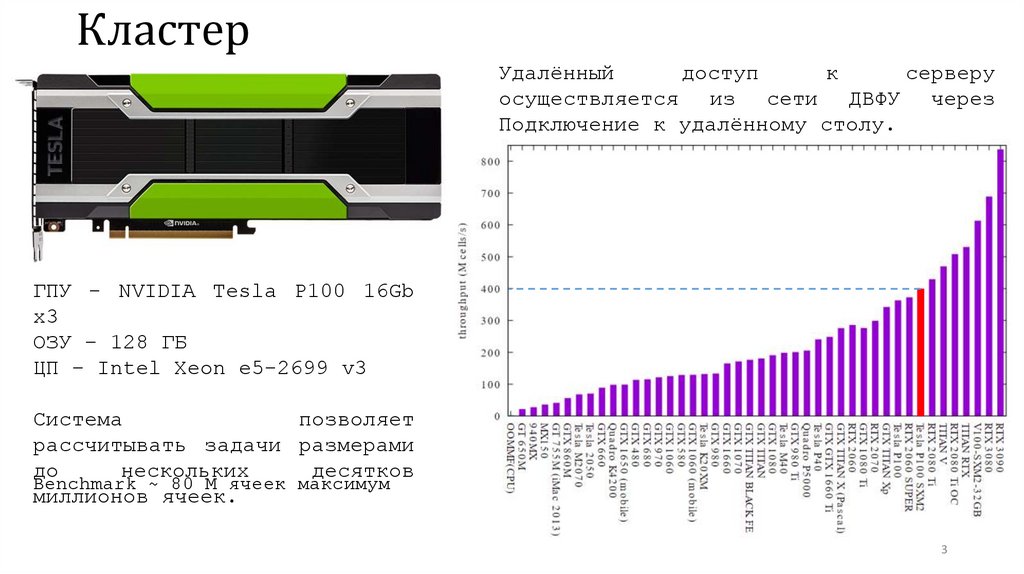
Кластер
Удалённый
доступ
к
серверу
осуществляется из сети ДВФУ через
Подключение к удалённому столу.
ГПУ - NVIDIA Tesla P100 16Gb
x3
ОЗУ – 128 ГБ
ЦП – Intel Xeon e5-2699 v3
Система
позволяет
рассчитывать задачи размерами
до
нескольких
десятков
Benchmark ~ 80 M ячеек максимум
миллионов ячеек.
3

4.

Бенчмарк
ГПУ - NVIDIA 2047MB NVIDIA GeForce
GTX 950M
msat = 800e3
aex = 13e-12
Бенчмарк ~ 7 M ячеек
alpha = 0.1
setcellsize(4e-9, 4e-9, 4e-9)
for e := 5; e < 100; e++ {
n := 128 * e
setgridsize(n, n, 1)
steps(1)
fprintln("mem.txt", n*n)
}
4

5.

Дополнительный софт
• MuView – лёгкая и простая программа для
трёхмерного
просмотра
.ovf
файлов.
Поддерживает
слайсинг,
вращение,
масштабирование
данных,
разные
цветовые
спектры.
• Работает только с векторными .ovf файлами
• Показывает
только
нормированную
часть
намагниченности
• https://github.com/grahamrow/Muview2/releases
Позволяет по выбранным настройкам визуализации
экспортировать серию .ovf данных

6.

Дополнительный софт
• OOMMF – позволяет просматривать .ovf файлы,
полученные с MuMax в модуле mmDisp. Может
просматривать как векторные данные, так и
скалярные поля величин (например E_total).
Так же может работать с ненормированными
векторами.
• Так же геометрию, задаваемую формулами в
OOMMF можно конвертировать в формат MuMax3.
Полезно при создании сложных геометрий,
которые проблематично задать логическими
операциями с примитивами.
• Визуализирует проекцию на одну из выбранных
осей, без поддержки 3D
https://math.nist.gov/oommf/
• OOMMFtools – набор дополнительных опций для
OOMMF.
Позволяет
работать
с
файлами
.config, записываемыми в клиенте OOMMF и

7.

Дополнительный софт
• ParaView – бесплатный и мощный 3-д
редактор.
Для работы в нём требуется конвертация
файла .ovf в .vts/vtk.
https://www.paraview.org
• Конвертор
.ovf
to
.vtk
https://fangohr.github.io/software/o
vf2vtk/index.html

8.

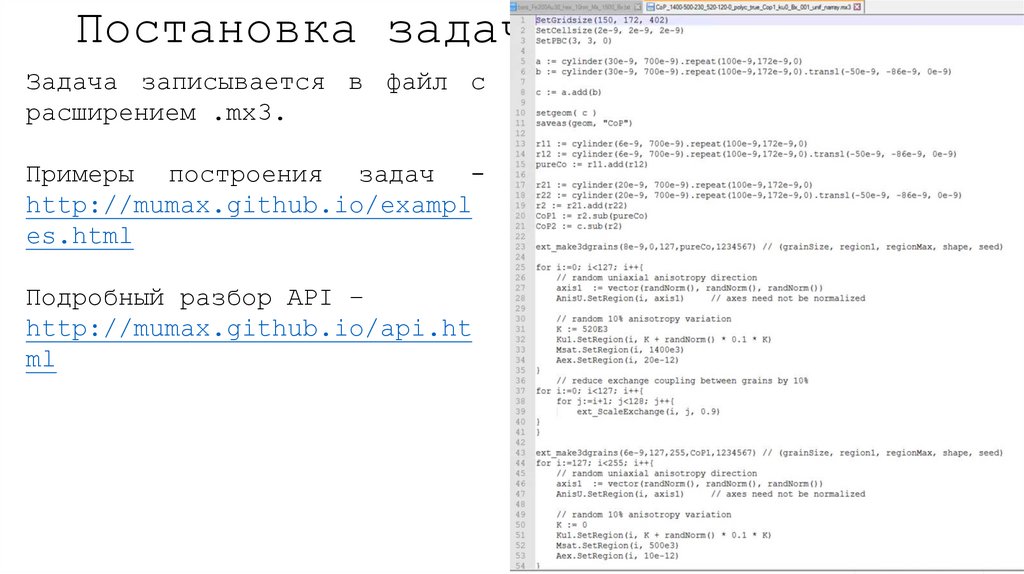
Постановка задачи
Задача записывается в файл с
расширением .mx3.
Примеры построения задач http://mumax.github.io/exampl
es.html
Подробный разбор API –
http://mumax.github.io/api.ht
ml

9.

Код можно условно разбить на
несколько блоков:
Блок
юниверса
–
задаёт
параметры пространства, в
котором будет проводиться
моделирование.
Блок
геометрии
–
задаёт
геометрию внутри юниверса,
которая будет в дальнейшем
обсчитываться.
Блок параметров материала –
задаёт внутренние параметры
материала.
Блок
конфигурации
намагниченности
–
задаёт
каким
будет
направление
намагниченности
в
каждой
ячейке
в
начале
эксперимента.
Минимайзер – каким методом
будет производиться поиск
минимума энергии системы.
Юниверс
Геометрия
Параметры материала
Конфигурация начальной намагниченности
Конфигурация минимайзера
Переменные цикла
Цикл 1
Цикл 2
Цикл 3

10.

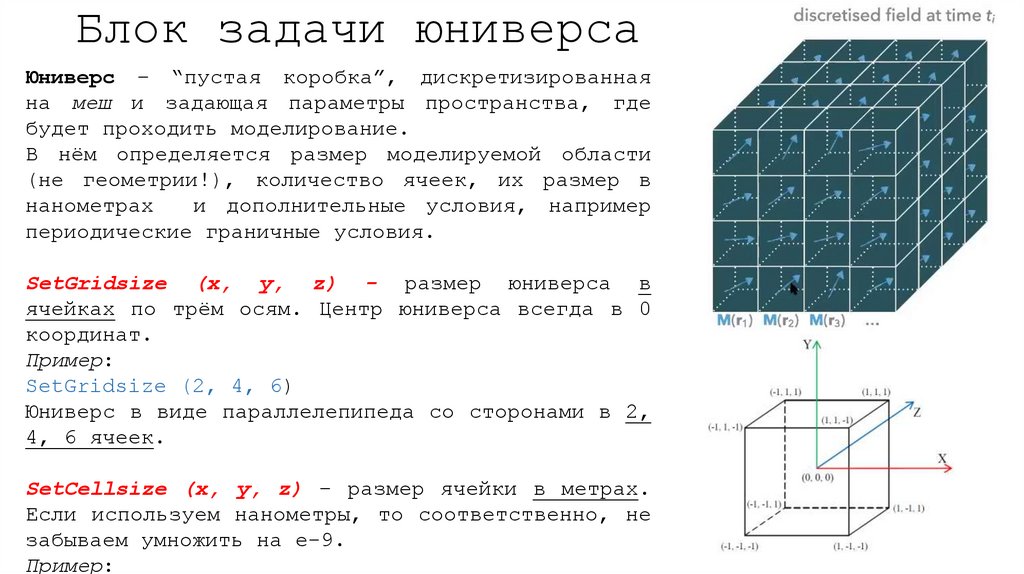
Блок задачи юниверса
Юниверс – “пустая коробка”, дискретизированная
на меш и задающая параметры пространства, где
будет проходить моделирование.
В нём определяется размер моделируемой области
(не геометрии!), количество ячеек, их размер в
нанометрах
и дополнительные условия, например
периодические граничные условия.
SetGridsize (x, y, z) - размер юниверса в
ячейках по трём осям. Центр юниверса всегда в 0
координат.
Пример:
SetGridsize (2, 4, 6)
Юниверс в виде параллелепипеда со сторонами в 2,
4, 6 ячеек.
SetCellsize (x, y, z) – размер ячейки в метрах.
Если используем нанометры, то соответственно, не
забываем умножить на e-9.
Пример:

11.

Блок задачи юниверса
SetPBC (x, y, z) – Periodic Boundary Conditions – периодические граничные
условия, указывают, сколько раз будет “фантомно” повторяться заданный нами
юниверс. Используется для создания условно-бесконечного юниверса путём
замыкания его самого на себя и расчётом магнитостатических полей на его
границах для избежания граничных эффектов. Используется, когда требуется
смоделировать лишь часть гораздо большего массива.
Пример:
SetPBC (1, 0, 0) – юниверс и геометрия в нём будет повторяться 1 раз по
оси x, и не повторяться по осям y и z.

12.

Блок геометрии
После задачи юниверса в него следует поместить геометрию
исследуемого
образца,
которой
потом
будут
задаваться
соответствующие параметры материала
SetGeom ( geom (x, y, z).logic(x, y, z).location(x, y, z))
Геометрия задаётся путём комбинации примитивных трёхмерных
геометрий (cuboid, cylinder, ellipsoid, image) с помощью
логических операций (add, and, sub, Xor) и операций перемещения
(repeat, transl, rotX)

13.

Блок геометрии
z
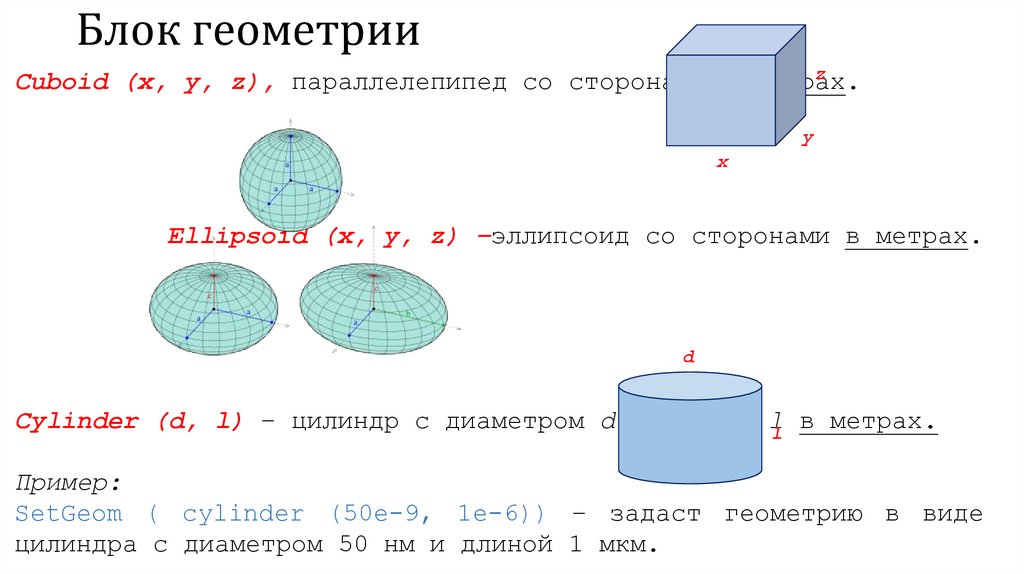
Cuboid (x, y, z), параллелепипед со сторонами в метрах.
y
x
Ellipsoid (x, y, z) –эллипсоид со сторонами в метрах.
d
Cylinder (d, l) – цилиндр с диаметром d и длиной l
в метрах.
l
Пример:
SetGeom ( cylinder (50e-9, 1e-6)) – задаст геометрию в виде
цилиндра с диаметром 50 нм и длиной 1 мкм.

14.

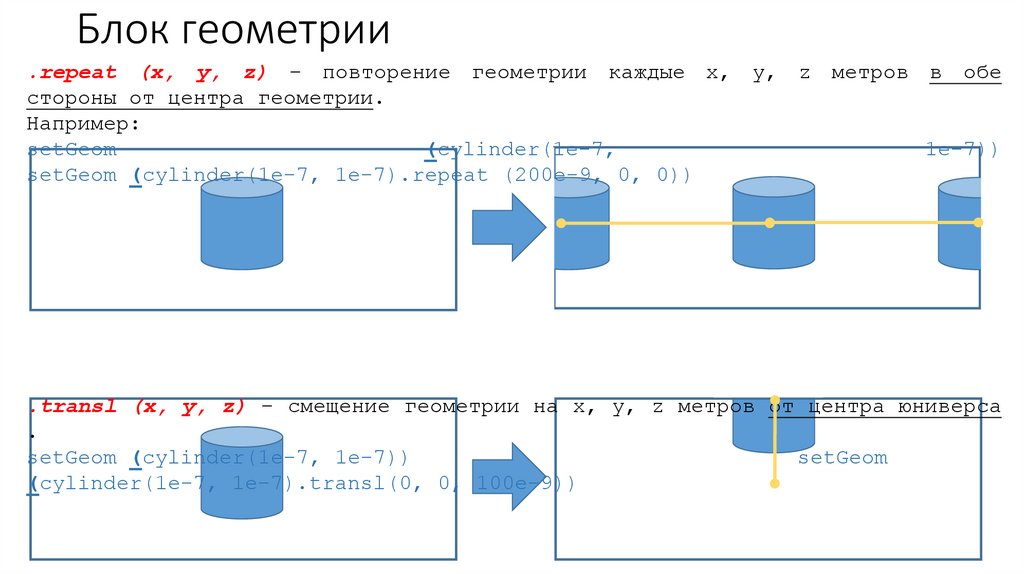
Блок геометрии
.repeat (x, y, z) – повторение геометрии каждые x, y, z метров в обе
стороны от центра геометрии.
Например:
setGeom
(cylinder(1e-7,
1e-7))
setGeom (cylinder(1e-7, 1e-7).repeat (200e-9, 0, 0))
.transl (x, y, z) – смещение геометрии на x, y, z метров от центра юниверса
.
setGeom (cylinder(1e-7, 1e-7))
setGeom
(cylinder(1e-7, 1e-7).transl(0, 0, 100e-9))

15.

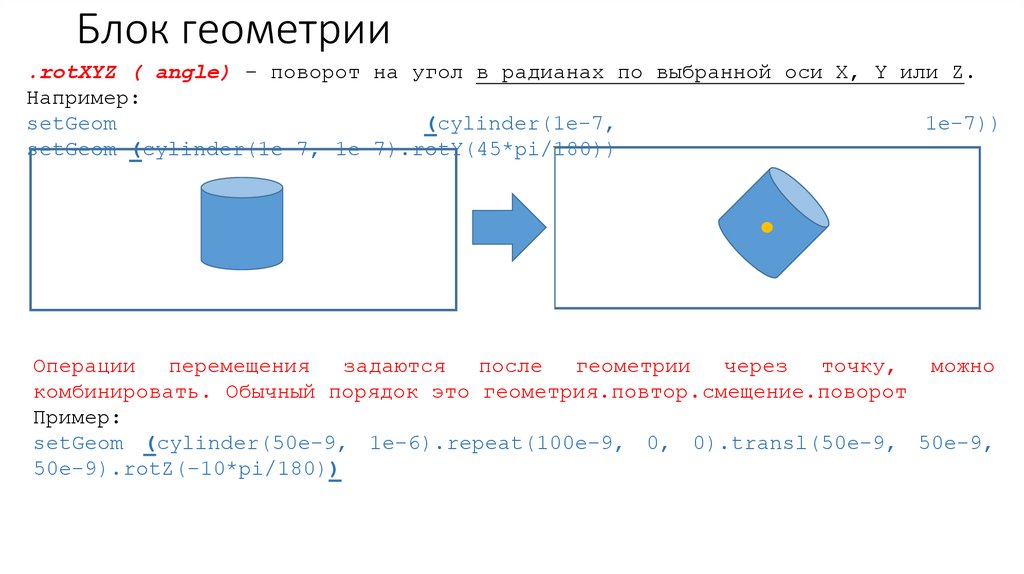
Блок геометрии
.rotXYZ ( angle) – поворот на угол в радианах по выбранной оси X, Y или Z.
Например:
setGeom
(cylinder(1e-7,
1e-7))
setGeom (cylinder(1e-7, 1e-7).rotY(45*pi/180))
Операции
перемещения
задаются
после
геометрии
через
точку,
можно
комбинировать. Обычный порядок это геометрия.повтор.смещение.поворот
Пример:
setGeom (cylinder(50e-9, 1e-6).repeat(100e-9, 0, 0).transl(50e-9, 50e-9,
50e-9).rotZ(-10*pi/180))

16.

Блок геометрии
Можно задавать переменные с любым названием
Например
a := Cuboid(100e-9, 100e-9, 100e-9).transl(50e-9, 0, 0)
b := Cylinder(50e-9, 100e-9).rotX(90*pi/180)
С заданными переменными можно работать с использованием логических операций
и трансляций формата переменная1.логическая_операция(переменная2)
Пример:
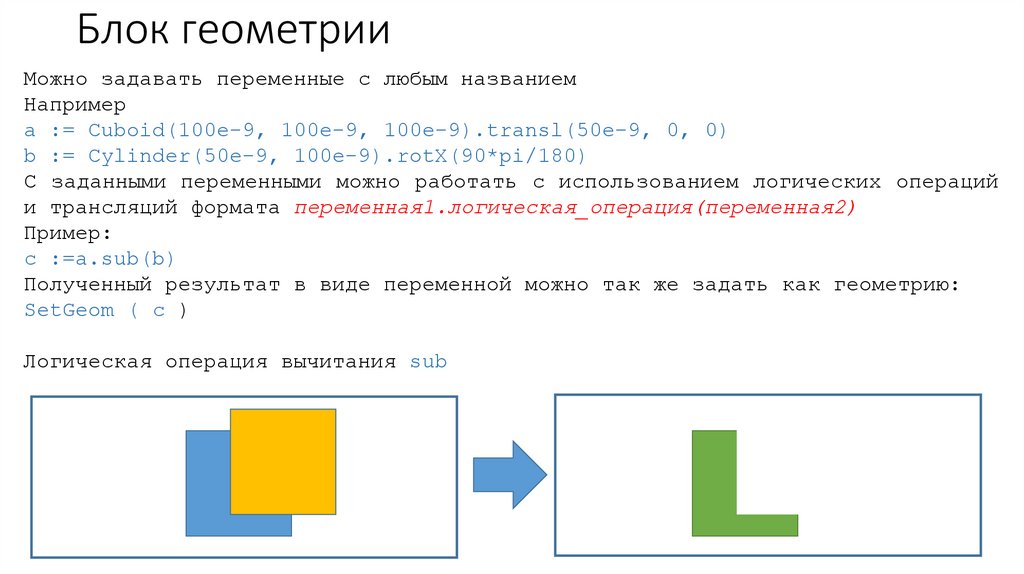
c :=a.sub(b)
Полученный результат в виде переменной можно так же задать как геометрию:
SetGeom ( c )
Логическая операция вычитания sub

17.

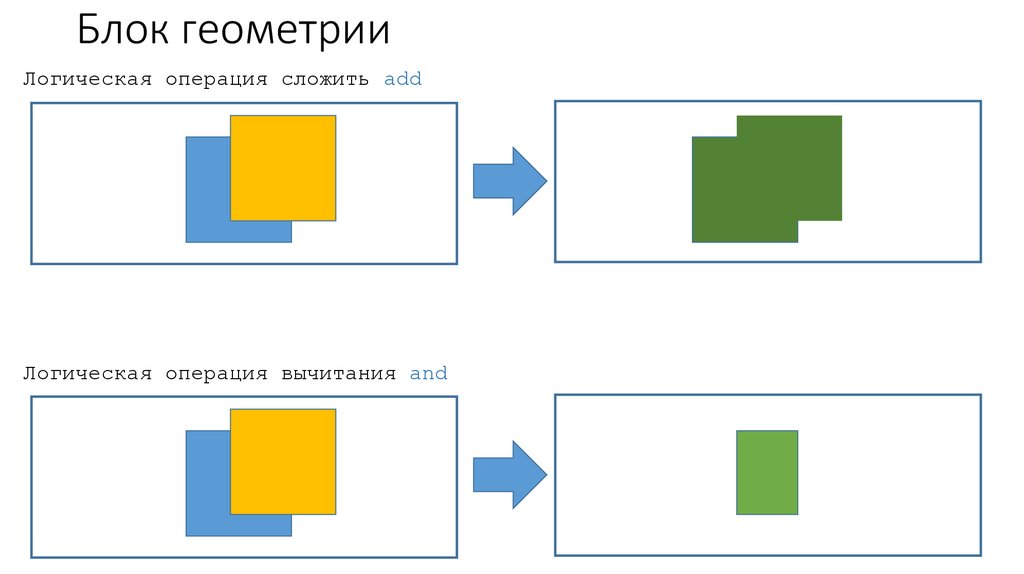
Блок геометрии
Логическая операция сложить add
Логическая операция вычитания and

18.

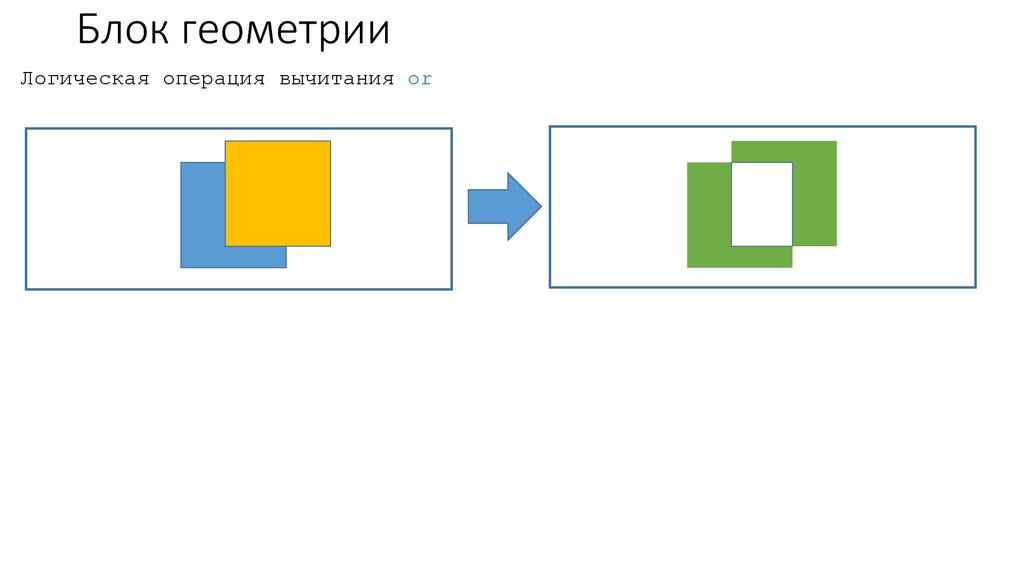
Блок геометрии
Логическая операция вычитания or

19.

Блок параметров материала
Параметры материалов записываются в системе С. И.
Msat – намагниченность насыщения в A/м
Aex – константа обменного взаимодействия в J/m
Kc1, Ku1, Ku2 – константы магнитокристаллической анизотропии в
J/m3)
AnisU(x,
y,
z)
–
вектор
магнитокристаллической анизотропии.
AnisC1(x, y, z), AnisC2(x, y,
магнитокристаллической анизотропии
alpha
- коэффициент затухания
T – температура в Кельвинах
направления
z)
–
вектора
одноосной
кубической

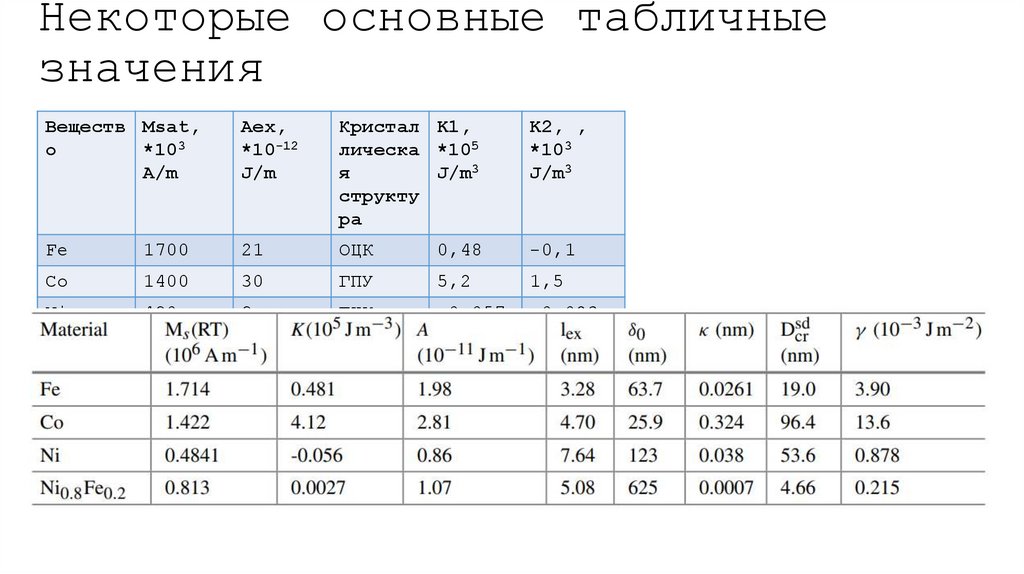
20.

Некоторые основные табличные
значения
Веществ Msat,
о
*103
A/m
Aex,
*10-12
J/m
Кристал K1,
лическа *105
я
J/m3
структу
ра
K2, ,
*103
J/m3
Fe
1700
21
ОЦК
0,48
-0,1
Co
1400
30
ГПУ
5,2
1,5
Ni
490
9
ГЦК
-0,057
-0,023

21.

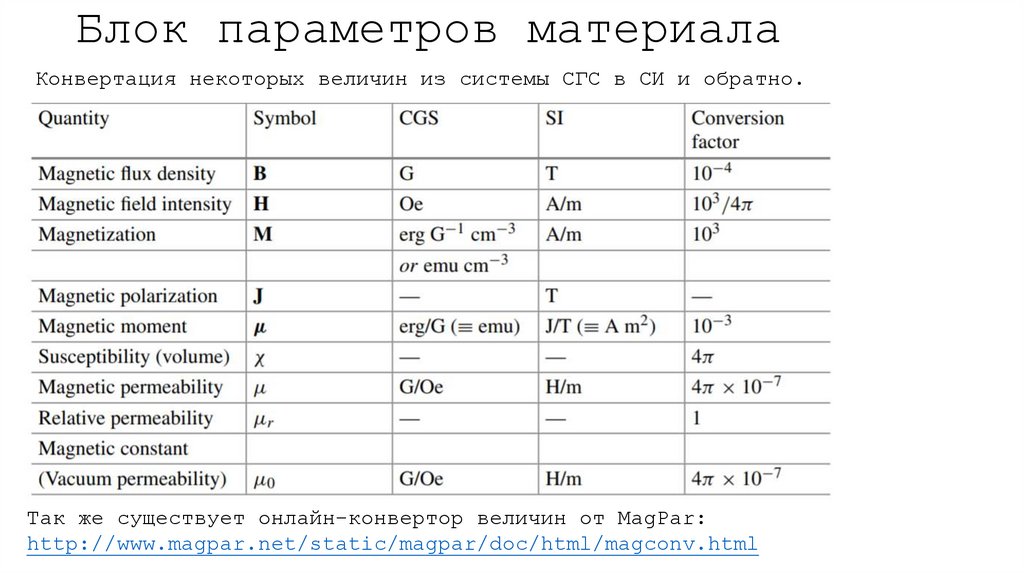
Блок параметров материала
Конвертация некоторых величин из системы СГС в СИ и обратно.
Так же существует онлайн-конвертор величин от MagPar:
http://www.magpar.net/static/magpar/doc/html/magconv.html

22.

Разбиение на регионы
Геометрическую форму можно принять за некий регион, с
определёнными свойствами:
DefRegion(N, n) – где N – номер региона от 0 до 256, и n
– название переменной, присвоенной ранее созданной
геометрии)
Например:
DefRegion(256, c)
После
определения
региона
в
нём
можно
прописать
специфичные свойства материалов:
Parameter.setRegion(n, a) – где Parameter – любой
параметр материала Msat, Aex, Ku1 etc., N – номер региона
и а – значение величины
Например:
DefRegion (256, c)
Msat.SetRegion(256, 230e3)
Aex.SetRegion(256, 21e-12)
Ku1.SetRegion(256, 5,2e5)
В таком случае, регион 256, определённый геометрией “с”

23.

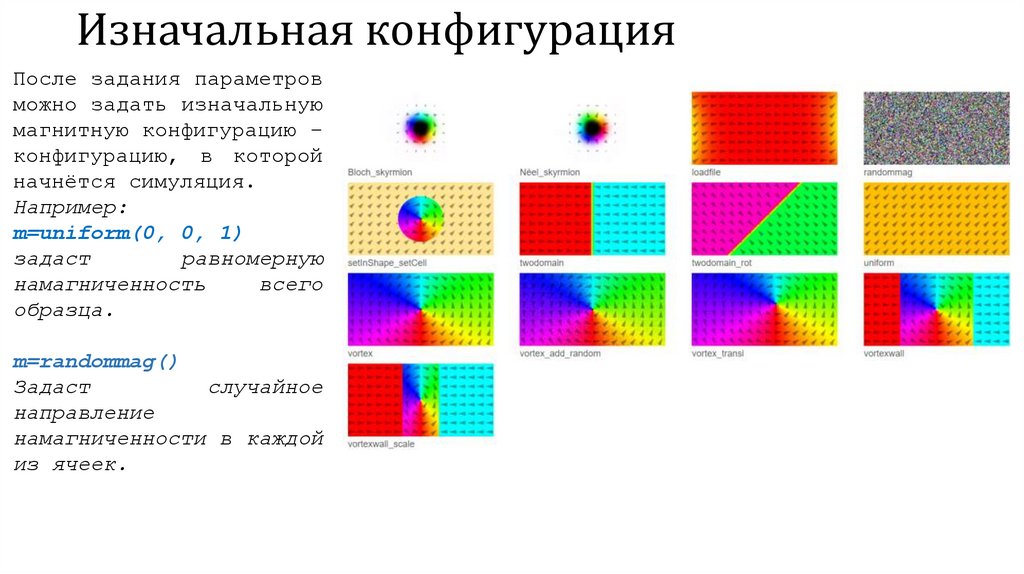
Изначальная конфигурация
После задания параметров
можно задать изначальную
магнитную конфигурацию –
конфигурацию, в которой
начнётся симуляция.
Например:
m=uniform(0, 0, 1)
задаст
равномерную
намагниченность
всего
образца.
m=randommag()
Задаст
случайное
направление
намагниченности в каждой
из ячеек.

24.

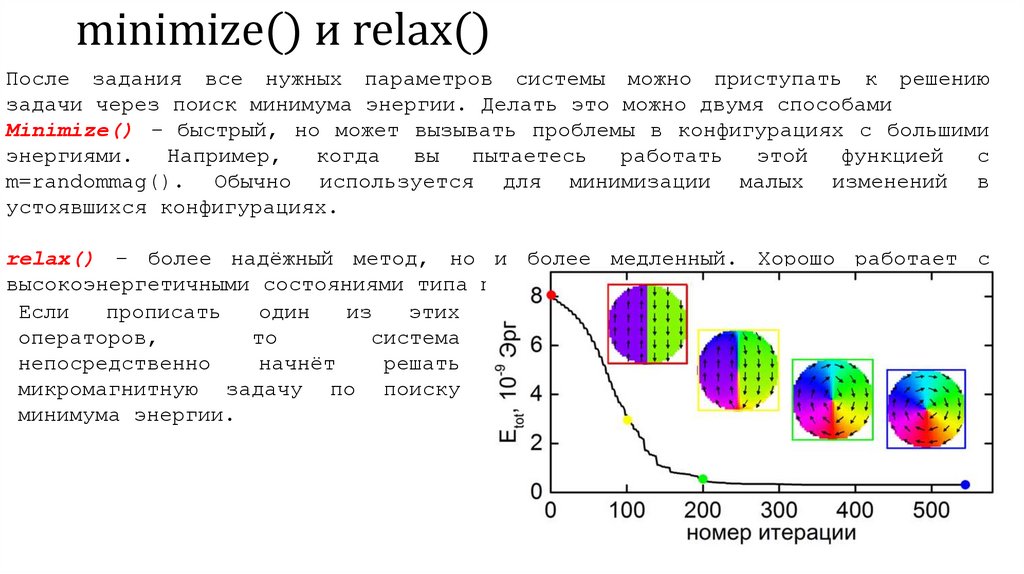
minimize() и relax()
После задания все нужных параметров системы можно приступать к решению
задачи через поиск минимума энергии. Делать это можно двумя способами
Minimize() – быстрый, но может вызывать проблемы в конфигурациях с большими
энергиями.
Например,
когда
вы
пытаетесь
работать
этой
функцией
с
m=randommag(). Обычно используется для минимизации малых изменений в
устоявшихся конфигурациях.
relax() – более надёжный метод, но и более медленный. Хорошо работает с
высокоэнергетичными состояниями типа m=randommag().
Если
прописать
один
из
этих
операторов,
то
система
непосредственно
начнёт
решать
микромагнитную задачу по поиску
минимума энергии.

25.

Сохранение результатов
После
решения
микромагнитной
задачи,
требуемый
параметр можно сохранить в виде векторного файла.
save (Х) – сохранит выходную переменную Х (например,
намагниченность m, полную энергию системы E_total,
размагничивающее поле B_demag и т.д.). В итоге
заданная
переменная
сохранится
в
файл
.ovf
с
автоматически заданными именем, в той папке, в которой
запускался исполняемый файл эксперимента .mx3
saveAs (X, “n”) – сохранит переменную Х с именем n.
tableSave() – сохранит численные значения в отдельный
файл
таблицы
table.txt.
Изначально
в
таблицу
сохраняется только магнитный момент по трём осям.
Чтобы записывать с таблицу другие значения, надо
прописать перед tableSave() строку tableAdd(X) – где Х
– любая выходная переменная.
Например
tableAdd(B_ext)
tableSave()

26.

Циклы
Цикл – повторяемая операция, выполняемая пока не будет
достигнуто
требуемое
условие.
Задаётся,
например,
следующим образом:
for X := a; X<=b; X+=c{
Тело цикла
}
Где X – изменяемая в цикле величина, а – начальное
значение величины, b – конечное значение величины, с –
шаг изменения величины.
X:= a значит, что цикл начинается с величины а, и
выполняется пока не достигнет условия X меньше либо
равно b; с шагом равным B+=с
В теле цикла, после { и до } записываются выполняемые
условия для каждого значения X.
Например, цикл для изменения магнитного поля от 0 до 0.1
Т с шагом 0.005 Т :
for B:=0; B<=0.1; B+=0.005{
B_ext = vector(B, 0, 0)
minimize()
save(m)

27.

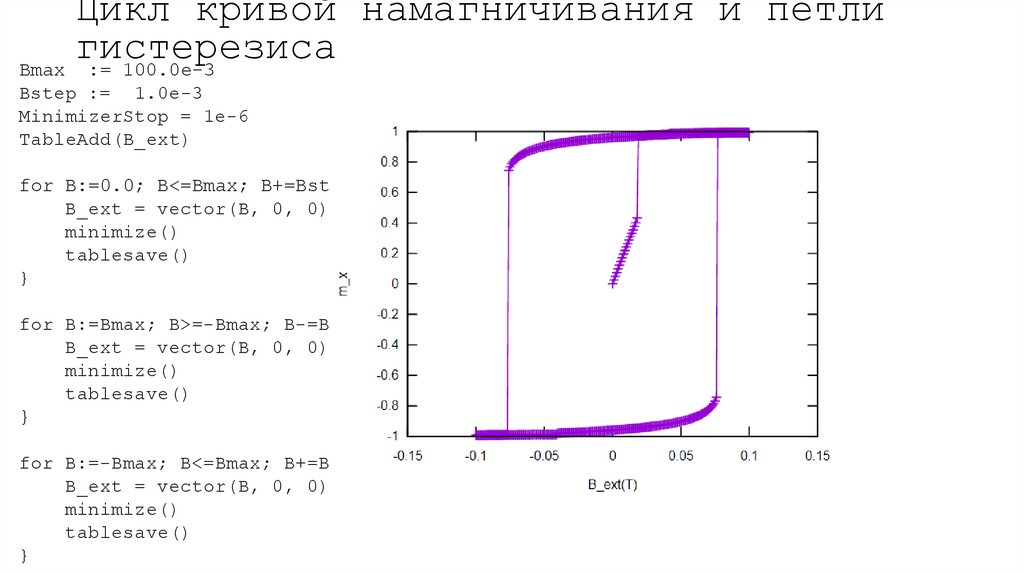
Цикл кривой намагничивания и петли
гистерезиса
Bmax := 100.0e-3
Bstep := 1.0e-3
MinimizerStop = 1e-6
TableAdd(B_ext)
for B:=0.0; B<=Bmax; B+=Bstep{
B_ext = vector(B, 0, 0)
minimize()
tablesave()
}
for B:=Bmax; B>=-Bmax; B-=Bstep{
B_ext = vector(B, 0, 0)
minimize()
tablesave()
}
for B:=-Bmax; B<=Bmax; B+=Bstep{
B_ext = vector(B, 0, 0)
minimize()
tablesave()
}

28.

Цикл разбиения Вороного
Используется для разбиения геометрии на трёхменый поликристалл
ext_make3dgrains(8e-9,0,127,pureCo,1234567) // (grainSize,
region1, regionMax, shape, seed)
for i:=0; i<127; i++{
// random uniaxial anisotropy direction
axis1 := vector(randNorm(), randNorm(), randNorm())
AnisU.SetRegion(i, axis1)
// axes need not be
normalized
// random 10% anisotropy variation
K := 520E3
Ku1.SetRegion(i, K + randNorm() * 0.1 * K)
Msat.SetRegion(i, 1400e3)
Aex.SetRegion(i, 20e-12)
}
// reduce exchange coupling between grains by 10%
for i:=0; i<127; i++{
for j:=i+1; j<128; j++{
ext_ScaleExchange(i, j, 0.9)

29.

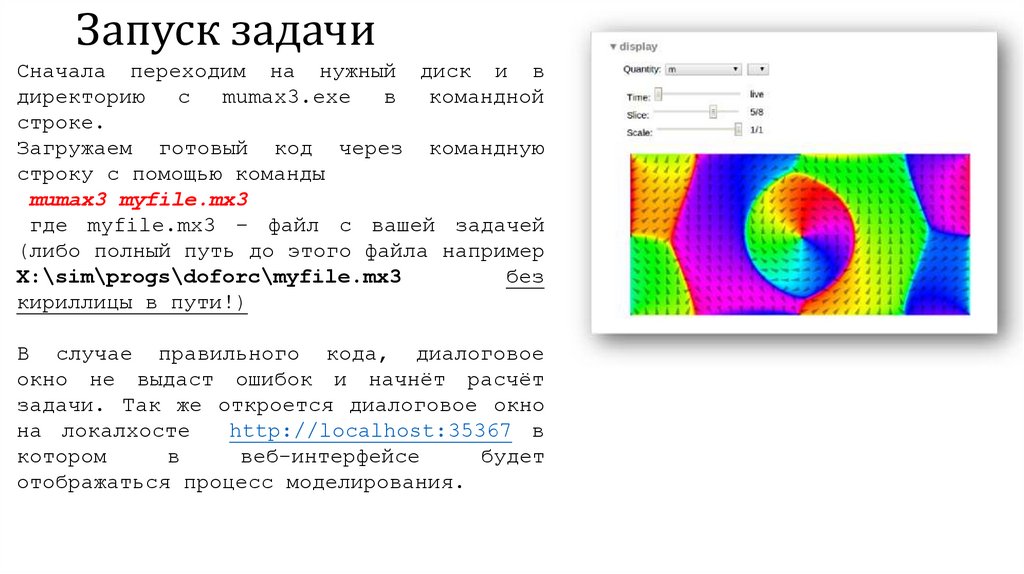
Запуск задачи
Сначала переходим на нужный диск и в
директорию
с
mumax3.exe
в
командной
строке.
Загружаем готовый код через командную
строку с помощью команды
mumax3 myfile.mx3
где myfile.mx3 – файл с вашей задачей
(либо полный путь до этого файла например
X:\sim\progs\doforc\myfile.mx3
без
кириллицы в пути!)
В случае правильного кода, диалоговое
окно не выдаст ошибок и начнёт расчёт
задачи. Так же откроется диалоговое окно
на локалхосте
http://localhost:35367 в
котором
в
веб-интерфейсе
будет
отображаться процесс моделирования.

30.

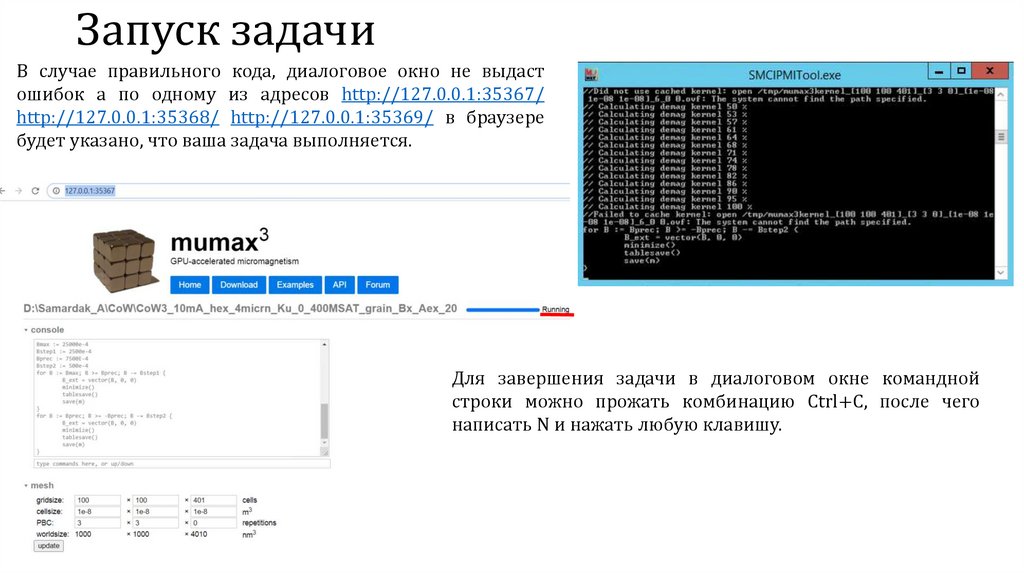
Запуск задачи
В случае правильного кода, диалоговое окно не выдаст
ошибок а по одному из адресов http://127.0.0.1:35367/
http://127.0.0.1:35368/ http://127.0.0.1:35369/ в браузере
будет указано, что ваша задача выполняется.
Для завершения задачи в диалоговом окне командной
строки можно прожать комбинацию Ctrl+C, после чего
написать N и нажать любую клавишу.

31.

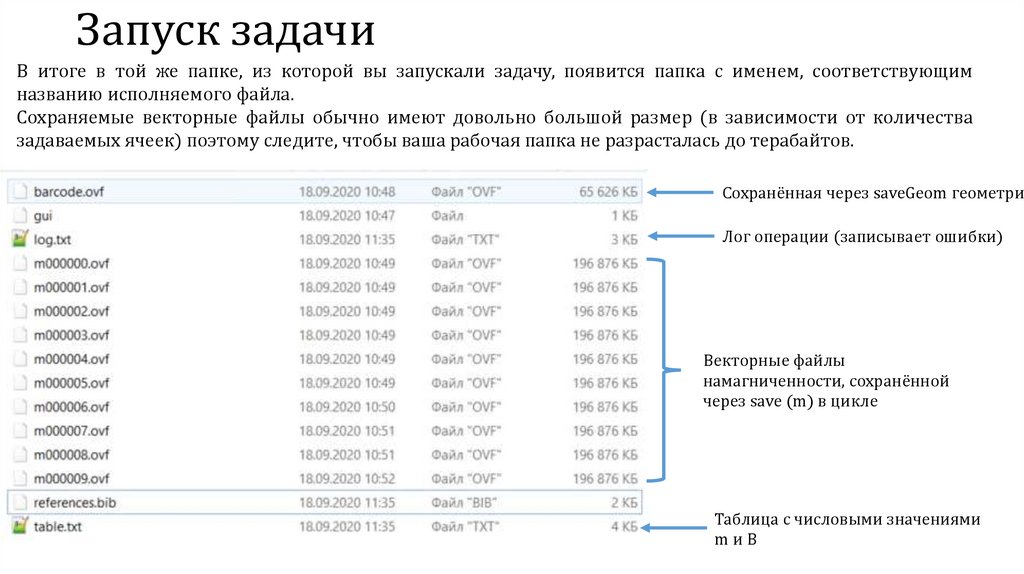
Запуск задачи
В итоге в той же папке, из которой вы запускали задачу, появится папка с именем, соответствующим
названию исполняемого файла.
Сохраняемые векторные файлы обычно имеют довольно большой размер (в зависимости от количества
задаваемых ячеек) поэтому следите, чтобы ваша рабочая папка не разрасталась до терабайтов.
Сохранённая через saveGeom геометрия
Лог операции (записывает ошибки)
Векторные файлы
намагниченности, сохранённой
через save (m) в цикле
Таблица с числовыми значениями
mиB

32.

samardak.aiu@dvfu.ru
32