Теория принятия решений. Методы решения задач линейного программирования. Динамическое программирование (лекция 1 - 4)

1.

Филиал ФГБОУ ВО
«Национальный исследовательский университет «МЭИ» в г. Смоленске
Теория принятия решений
Доцент кафедры ВТ
кандидат технических наук, доцент
И.А. Денисова
Смоленск
Смоленск
– 2024
2011

2.

Лекция № 1
Основы теории принятия решений

3.

УЧЕБНЫЕ ВОПРОСЫ
1. Основы теории принятия решений.
2. Исследование операций. Математические модели
операций.

4.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Составить математическую модель задачи ЛП
Для изготовления двух видов изделий А и Б используют три вида сырья.
На производство единицы изделия А требуется затратить сырья 1-го вида 13
кг, сырья 2-го вида 32 кг, сырья 3-го вида 58 кг. На производство единицы
изделия Б требуется затратить сырья 1-го вида 24 кг, сырья 2-го вида 32 кг,
сырья 3-го вида 29 кг. Производство обеспечено сырьем 1-го вида в
количестве 312 кг, сырья 2-го вида 480 кг, сырья 3-го вида 696 кг. Прибыль от
реализации единицы готового изделия А составляет 4 усл. ед., от
реализации единицы готового изделия Б – 3 усл. ед.
Требуется составить план производства изделий А и Б, обеспечивающий
максимальную прибыль от их реализации, если заранее планируется
изготовить не менее 10 единиц изделий А и Б (суммарно).
2. Решить задачу ЛП.
4

5.

Лекция № 2
Методы решения задач линейного
программирования

6.

УЧЕБНЫЕ ВОПРОСЫ
1. Общая характеристика методов решения задач линейного
программирования
2. Симплекс-метод решения
основной задачи линейного программирования
3. Венгерский метод решения
задачи о назначениях линейного программирования

7.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Решить симплекс-методом задачу линейного программирования.
L=6x1+5x2 +5x3 →max
3x1+6x2+4x3 180
2x1+x2 +2x3 50
2x1+3x2+x3 40
x1 0
x2 0
x3 0
7

8.

Лекция № 3
Задачи транспортного типа
и методы их решения

9.

УЧЕБНЫЕ ВОПРОСЫ
1. Задачи линейного программирования транспортного типа
2. Метод потенциалов решения транспортной задачи

10.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Решить методом потенциалов задачу линейного программирования
транспортного типа
2 4 5 7 9
С= 1 6 3 5 4 , a=(300; 400; 900), b=(250; 300; 350; 500; 200)
6 3 2 1 10
10

11.

Лекция № 4
Динамическое программирование
в задачах принятия решений

12.

УЧЕБНЫЕ ВОПРОСЫ
1. Метод динамического программирования (ДП)
2. Решение задач принятия решений методом ДП

13.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Построить граф и решить задачу о кратчайшем пути методом ДП
Из
В
1
2
3
4
5
6
7
8
9
2
5
3
3
4
4
5
5
6
7
7
3
1
15
2
6
4
2
9
8
10
4
5
9
10
10
11
8
4
2
7
6
3
13

14.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 2. Решить задачу о наборе высоты методом ДП
25
14
27
15
25
12
16
27
12
23
11
14
24
11
23
11
21
27
24
23
17
13
11
10
27
11
25
9
22
9
21
14

15.

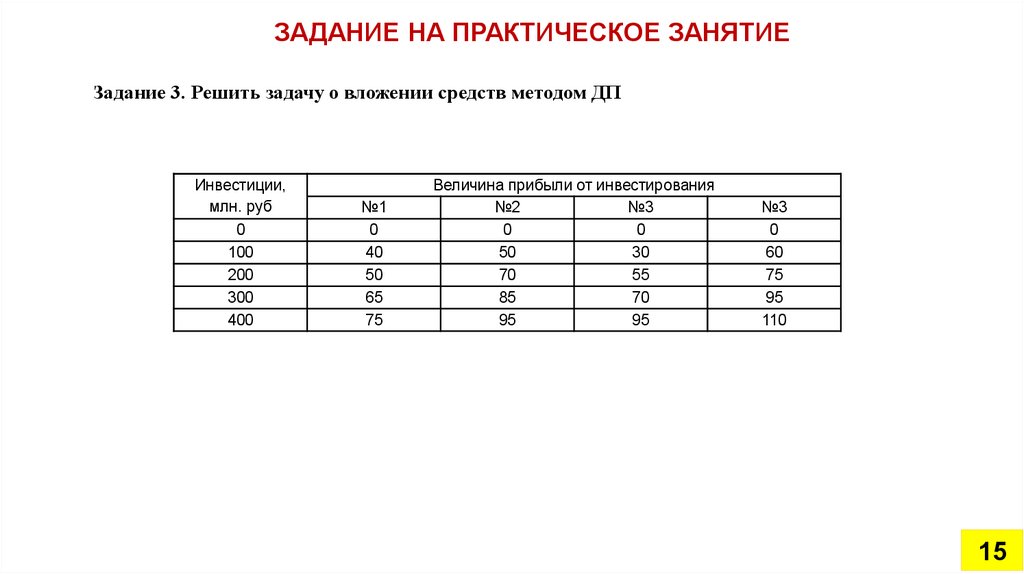
ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 3. Решить задачу о вложении средств методом ДП
Инвестиции,
млн. руб
0
100
200
300
400
№1
0
40
50
65
75
Величина прибыли от инвестирования
№2
№3
0
0
50
30
70
55
85
70
95
95
№3
0
60
75
95
110
15

16.

Лекция № 5
Многокритериальные задачи
принятия решений

17.

УЧЕБНЫЕ ВОПРОСЫ
1. Многокритериальные задачи (МКЗ) принятия решений
2. Методы решения МКЗ

18.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 1. Максимизировать
f1(X)= -x1+ 2x2,
f2(X) = 2x1 + x2,
f3(X)= x1 - 3х2
при условиях
х1 + x2 ≤ 6
1≤ x1 ≤ 3
1≤ x2 ≤ 4
методами
•главного критерия;
•линейной свертки с равными весами;
•последовательных уступок, если величины уступок: ∆1 = 3; ∆2 = 5/3.
18

19.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Правительство области назначило комиссию по выбору места для аэропорта, которая приступила
к работе. Были обследованы различные площадки около города, где постройка аэропорта нужного
размера представлялась возможной. После многочисленных дискуссий комиссия определила три
основных критерия для оценки вариантов расположения аэропорта.
1. Стоимость постройки. Желательно построить аэропорт с заданной пропускной
способностью за наименьшую возможную цену.
2. Расстояние от города. Желательно, чтобы поездка пассажиров от аэропорта в город и
обратно занимала наименьшее время.
3. Минимальное шумовое воздействие. Количество людей, подвергающихся нежелательным
шумовым воздействиям, должно быть, по возможности, минимальным.
В результате исследования получены четыре альтернативы со следующими оценками:
А ( 180 млн, 70 мин., 10 тыс.);
В ( 170 млн, 40 мин., 15 тыс.);
С ( 160 млн, 55 мин., 20 тыс.);
D ( 150 млн, 50 мин., 25 тыс.).
Решить методом последовательных уступок, если величины уступок: ∆1 = 20 млн. руб.; ∆2 = 10 мин.
19

20.

Лекция № 6
МЕТОДЫ ОЦЕНКИ МНОГОКРИТЕРИАЛЬНЫХ АЛЬТЕРНАТИВ

21.

УЧЕБНЫЕ ВОПРОСЫ
1. Метод ELECTRE
2. Методы экспертных оценок

22.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 1. Правительство области назначило комиссию по выбору места для аэропорта, которая
приступила к работе. Были обследованы различные площадки около города, где постройка аэропорта
нужного размера представлялась возможной. После многочисленных дискуссий комиссия определила
три основных критерия для оценки вариантов расположения аэропорта.
1. Стоимость постройки. Желательно построить аэропорт с заданной пропускной
способностью за наименьшую возможную цену.
2. Расстояние от города. Желательно, чтобы поездка пассажиров от аэропорта в город и
обратно занимала наименьшее время.
3. Минимальное шумовое воздействие. Количество людей, подвергающихся нежелательным
шумовым воздействиям, должно быть, по возможности, минимальным.
В результате исследования получены четыре альтернативы со следующими оценками:
А ( 180 млн, 70 мин., 10 тыс.);
В ( 170 млн, 40 мин., 15 тыс.);
С ( 160 млн, 55 мин., 20 тыс.);
D ( 150 млн, 50 мин., 25 тыс.).
Решить методом ELECTRE, если величины w1 = 0,65; w2 = 0,20; w3 = 0,15.
22

23.

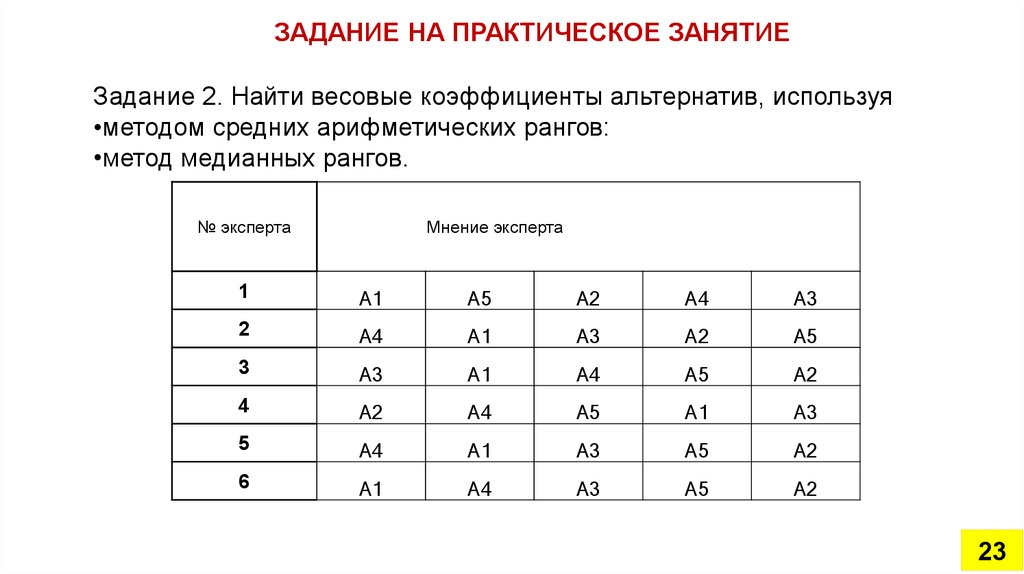
ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 2. Найти весовые коэффициенты альтернатив, используя
•методом средних арифметических рангов:
•метод медианных рангов.
№ эксперта
Мнение эксперта
1
А1
А5
А2
А4
А3
2
А4
А1
А3
А2
А5
3
А3
А1
А4
А5
А2
4
А2
А4
А5
А1
А3
5
А4
А1
А3
А5
А2
6
А1
А4
А3
А5
А2
23

24.

Лекция № 7
ПРИНЯТИЕ РЕШЕНИЙ В КОНФЛИКТНЫХ СИТУАЦИЯХ

25.

УЧЕБНЫЕ ВОПРОСЫ
1. Теория игр
2. Матричные игры и методы их решения
3. Статистические игры и методы их решения

26.

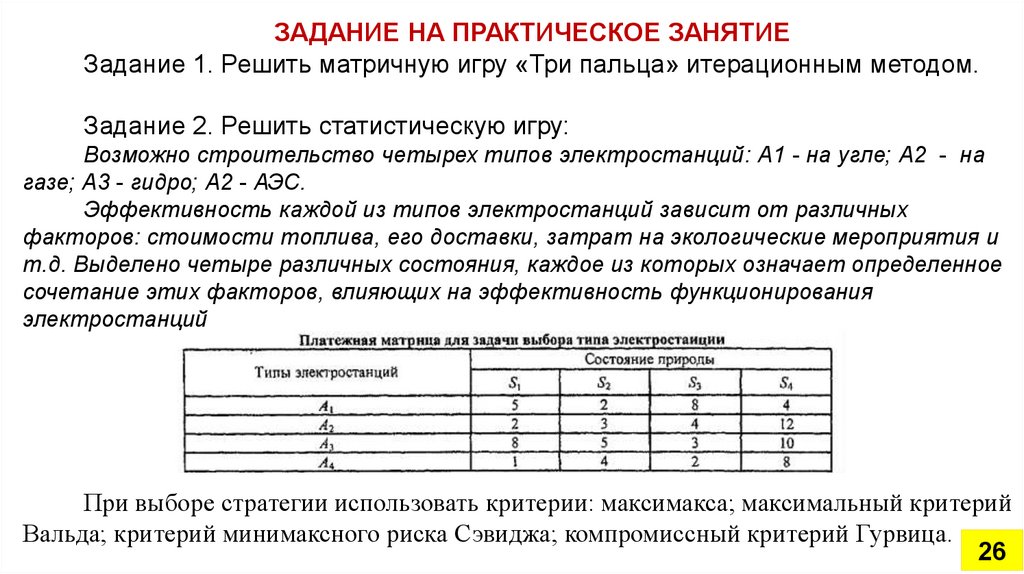
ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 1. Решить матричную игру «Три пальца» итерационным методом.
Задание 2. Решить статистическую игру:
Возможно строительство четырех типов электростанций: А1 - на угле; А2 - на
газе; А3 - гидро; А2 - АЭС.
Эффективность каждой из типов электростанций зависит от различных
факторов: стоимости топлива, его доставки, затрат на экологические мероприятия и
т.д. Выделено четыре различных состояния, каждое из которых означает определенное
сочетание этих факторов, влияющих на эффективность функционирования
электростанций
При выборе стратегии использовать критерии: максимакса; максимальный критерий
Вальда; критерий минимаксного риска Сэвиджа; компромиссный критерий Гурвица.
26

27.

Лекция № 8
ПРИНЯТИЕ РЕШЕНИЙ В КОНФЛИКТНЫХ СИТУАЦИЯХ

28.

УЧЕБНЫЕ ВОПРОСЫ
1. Статистические игры и методы их решения
2. Позиционные игры. Деревья принятия решений
3. Теория полезности и функции Неймана-Моргенштерна

29.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Задание 1. Решить статистическую игру:
Фирма «Фармацевт» - производитель медикаментов и биомедицинских изделий в регионе. Известно, что пик
спроса на некоторые лекарственные препараты приходится на летний период (препараты сердечно-сосудистой
группы, анальгетики), на другие – на осенний и весенний периоды (антиинфекционные, противокашлевые).
Затраты за 1 усл.ед. продукции за сентябрь-октябрь составили: по первой группе (препараты сердечнососудистые и анальгетики) – 20 руб.; по второй группе (антиинфекционные, противо-кашлевые препараты) – 15 руб.
По данным наблюдений за несколько последних лет службой маркетинга фирмы установлено, что она может
реализовать в течение рассматриваемых двух месяцев в условиях теплой погоды 3050 усл.ед. продукции первой
группы и 1100 усл.ед. продукции второй группы; в условиях холодной погоды – 1525 усл.ед. продукции первой группы и
3690 усл.ед. второй группы.
В связи с возможными изменениями погоды ставится задача – определить стратегию фирмы в выпуске
продукции, обеспечивающую максимальный доход от реализации при цене продажи 40 руб. за 1 усл.ед. продукции первой
группы и 30 руб. – второй группы.
Фирма располагает двумя стратегиями по производству и дальнейшей реализации препаратов двух групп:
А1 - произвести 3050 усл.ед. препаратов 1 группы и 1100 усл.ед. препаратов 2 группы (производитель
предполагает, что будет теплая погода);
А2 – произвести 1525 усл.ед. препаратов 1 группы и 3690 усл.ед. препаратов 2 группы (производитель
предполагает, что будет холодная погода).
Выбрать оптимальную стратегию.
При выборе стратегии использовать критерии: максимакса; максимальный критерий Вальда; критерий
минимаксного риска Сэвиджа; компромиссный критерий Гурвица (α.=0,6).
29