Множества. Понятие и способы задания множеств

1.

Множества
Историческая справка
Понятие и способы задания множеств
Основные аксиомы
Операции над множествами
Свойства операций над множествами
Мощности конечных множеств
Декартово произведение

2. Историческая справка

Историческая справка
Родоначальником теории множеств считают Больцано. Он
определил множества, конечные и бесконечные, понятие взаимно
однозначного
соответствия,
понятие
предельной
точки
последовательности («Парадоксы бесконечного», 1850). К понятию
числовых множеств и множеств функций подводят некоторые
работы Римана, Дюбуа, Дедекинда. Кантор сделал решительный
шаг и начал изучать множества произвольной природы, он развил
методы, свойственные современной теории множеств, и поставил
ее на строго научную основу.

3. Историческая справка

«Множество есть
многое, мыслимое
нами как единое»
Основоположник
теории множеств,
немецкий математик
Георг Кантор
(1845-1918)

4. Понятие и способы задания множеств

Определение

5. Понятие и способы задания множеств

Определение

6. Понятие и способы задания множеств

Определение

7. Понятие и способы задания множеств

8. Понятие и способы задания множеств

9. Основные аксиомы

Определение
Для каждого множества А существует множество, элементами
которого являются только все его подмножества. Такое
множество называют семейством множества А или булеаном А и
обозначают В(А), а множество А, при этом, называют
пространством.
Теория множеств строится на основе следующих
утверждений, принимаемых без доказательства.
аксиом
–
Аксиомаобъемности
существования
Аксиома
существования
пустого множества
степени
объединения
дополнения
Если
множества
А имножеств
В составлены
из В
одних
и тех же
Для
произвольных
множеств
А множество.
и
существует
Существует
по крайней
мере одно
Для
произвольных
А
и
В
существует
Для
любого то
множества
А
существует
семейство
элементов,
они
совпадают
(равны):
А
=
В.
множество,
элементами
которого
являются
все
множество,
элементами
которого
являются
те
и
только
Существует
множество,
не
содержащее
ни
одного
элемента.
множеств множества
В(А) (булеан),
элементами
которого
являются
элементы
А
и
все
элементы
множества
В и
те
элементы
множества
А,
которые
не
являются
все подмножества
множества
А. не содержит.
которое
никаких
других
элементов
элементами множества В.

10. Операции над множествами

На базе аксиом можно ввести основные операции над
множествами.
1

11. Операции над множествами

2

12. Операции над множествами

3

13. Операции над множествами

4
А x x U \ A

14. Операции над множествами

Пример

15. Операции над множествами

16. Операции над множествами

17. Свойства операций над множествами

Для любых подмножеств А, В и С универсального множества U
выполняются следующие основные свойства операций над
множествами:
1.a
A B B A (коммутативность )
1.б
A B B A (коммутативность )
2.а
A B С А В С (ассоциативность )
2.б
A B С А В С (ассоциативность )
3.а
A B С А В А С (дистрибутивность
относительно )
3.б
A B С А В А С (дистрибутивность
относительно )

18. Свойства операций над множествами

4.a
A А U
5.a
A
6.а
7.а
4.б
A А
5.б
A U А
A A А
6.б
A A А
A U U
7.б
A
A
8.a
A B A B (закон двойственности – закон де Моргана)
8.б
A B A B (закон двойственности – закон де Моргана)
9.a
A A B A (закон поглощения)
9.б
A A B A (закон поглощения)
10
A A (закон двойного отрицания)
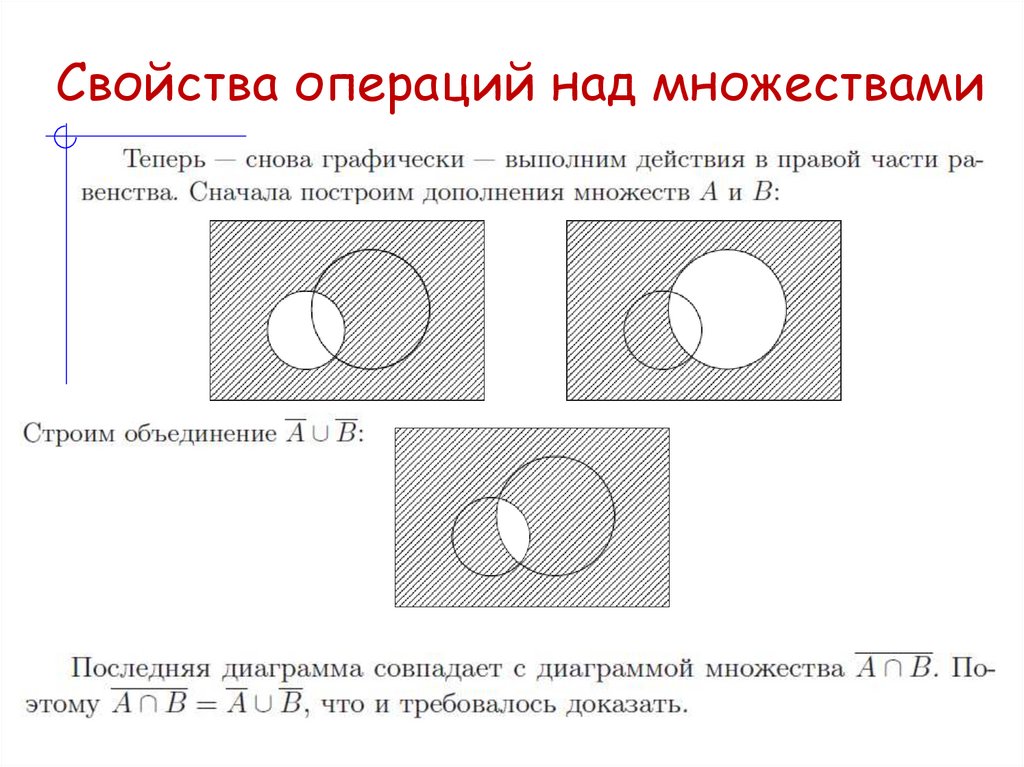
Справедливость тождеств легко устанавливается при помощи диаграмм
Эйлера-Венна, показывающих, что стоящие в левой и правой частях
тождества множества состоят из одних и тех же элементов.

19. Свойства операций над множествами

Пример

20. Свойства операций над множествами

21. Мощности конечных множеств

22. Мощности конечных множеств

23. Мощности конечных множеств

24. Мощности конечных множеств

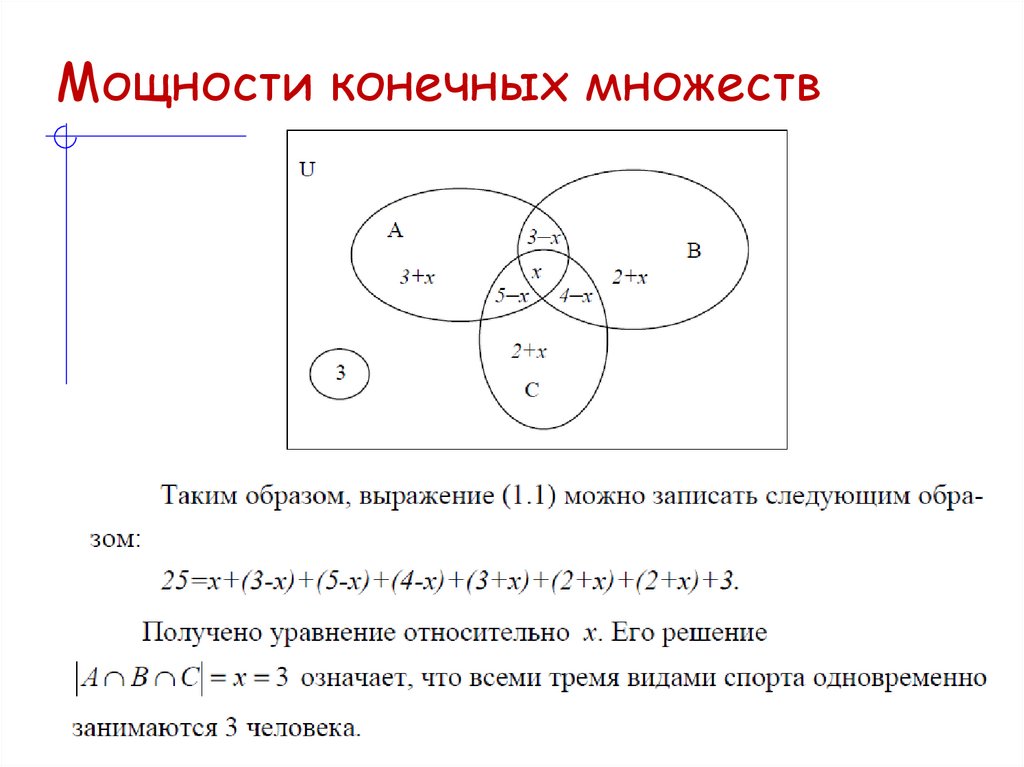
25. Мощности конечных множеств

26. Мощности конечных множеств

27. Декартово (прямое) произведение

Декартовым или прямым произведением множеств A и B называется
множество
Декартовым или прямым
называется множество
произведением
A1 A2 ... An x1, x2 ,..., xn
множеств
A1,A2,...,An
x1 A1 , x2 A2 ,..., xn An .
Если выполнено равенство A1 A2 ... An A, то прямое произведение
A1 A2 ... An An
и называется n-ой степенью множества А.
Положим по определению
Если хотя бы одно из множеств Ai пусто, то
A1 A2 ... An

28. Декартово произведение

29. Декартово произведение

Пример
Пример

30. Декартово произведение

Теорема
Пусть A1 , A2 , ..., An - конечные множества, их мощности
соответственно равны A1 k1, A2 k2 , ..., An kn . Тогда мощность
множества A1 A2 ... An равна произведению мощностей
множеств A1 , A2 , ..., An
A1 A2 ... An k1 k2 ... kn
Следствие
A A
n
n