Графики функций. Задание 11 ЕГЭ - профильного уровня по математике

1.

«Задание 11 ЕГЭ-профильного
уровня по математике
(графики функций)

2.

Способы решения:
1. Нахождение коэффициентов функции через решение систем
уравнений, используя целочисленные координаты точек
графика ( в том числе и точек пересечения с осями).
2. Нахождение коэффициентов, используя вспомогательные
формулы. Например, формулу тангенса угла наклона прямой,
абсциссы вершины параболы, периодичности функции и др.)
3. Преобразование формулы, задающую функцию.
4. Нахождение коэффициентов через преобразования
графиков функций.

3.

Линейная функция, её график
Линейная функция — функция вида y = kx+b.
График линейной функции — прямая.
Для построения графика линейной функции достаточно двух
точек — потому что через две несовпадающие точки всегда
можно провести прямую, причем единственную.

4.

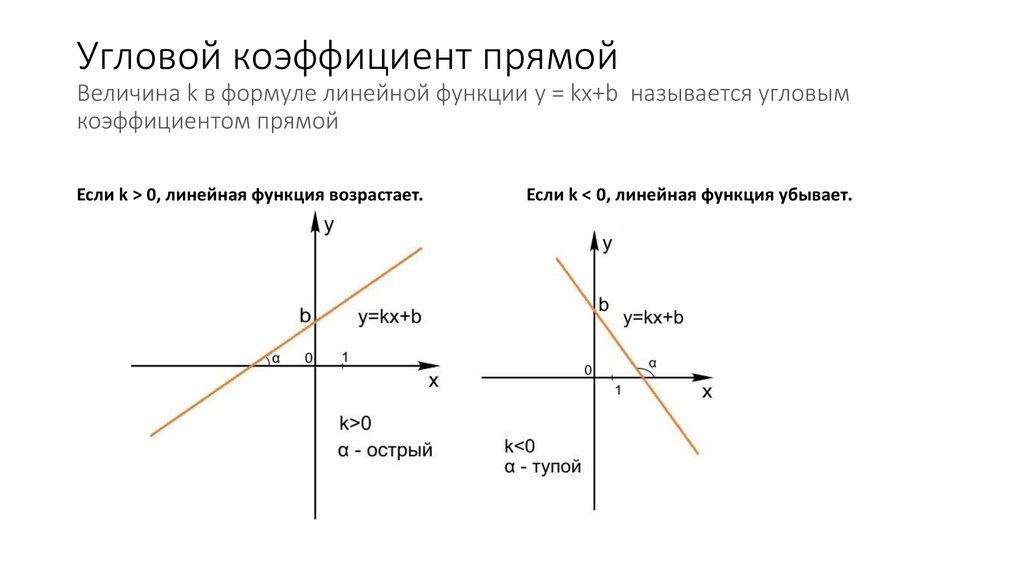
Угловой коэффициент прямой
Величина k в формуле линейной функции y = kx+b называется угловым
коэффициентом прямой
Если k > 0, линейная функция возрастает.
Если k < 0, линейная функция убывает.

5.

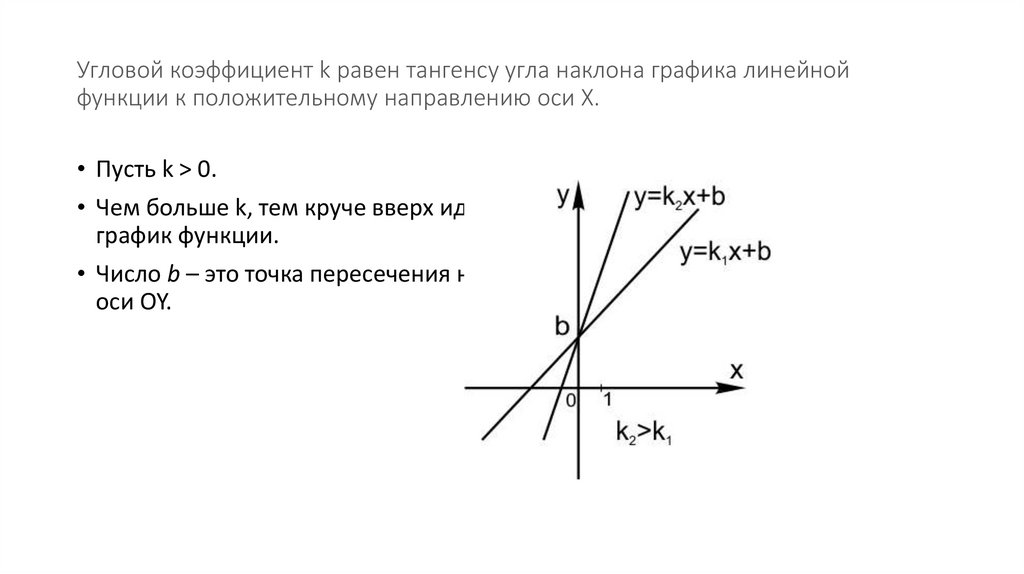
Угловой коэффициент k равен тангенсу угла наклона графика линейной
функции к положительному направлению оси Х.
• Пусть k > 0.
• Чем больше k, тем круче вверх идет
график функции.
• Число b – это точка пересечения на
оси OY.

6.

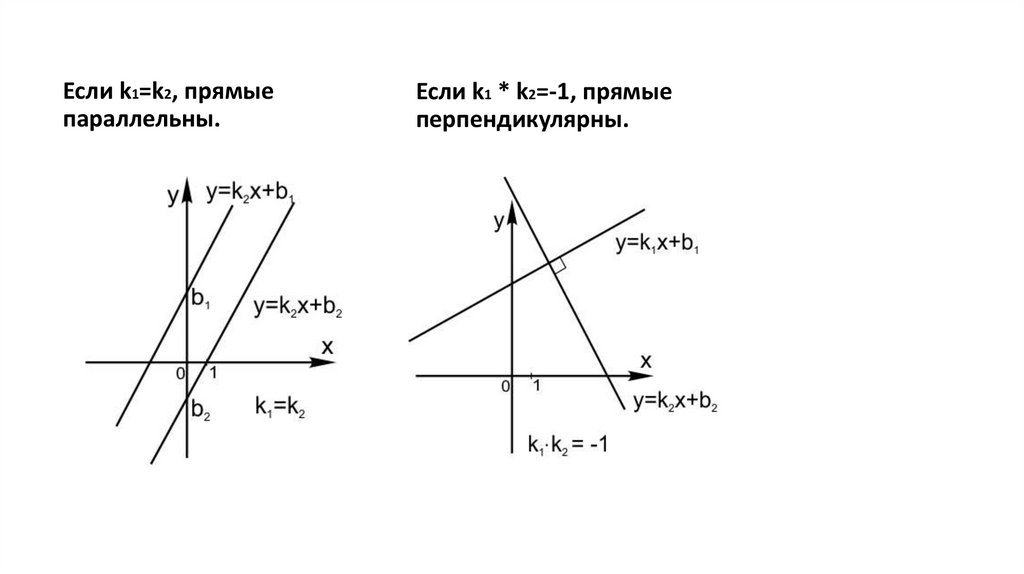
Если k1=k2, прямые
параллельны.
Если k1 * k2=-1, прямые
перпендикулярны.

7.

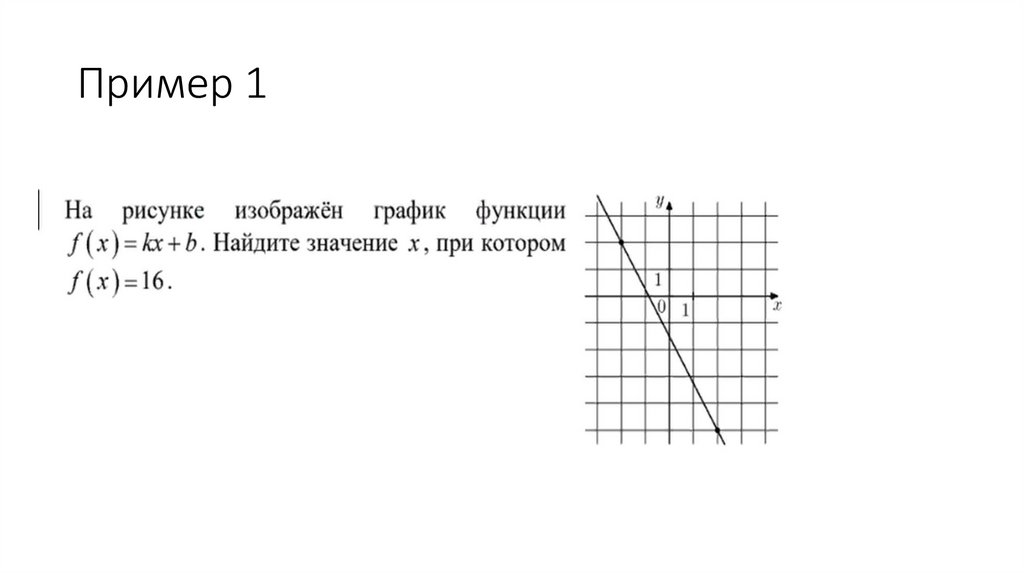
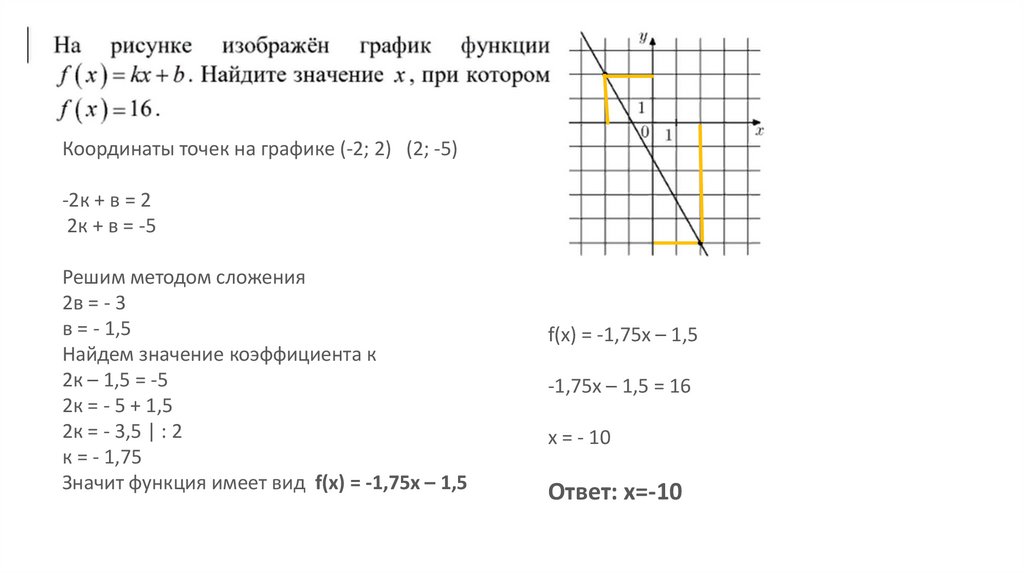
Пример 1

8.

Координаты точек на графике (-2; 2) (2; -5)
-2к + в = 2
2к + в = -5
Решим методом сложения
2в = - 3
в = - 1,5
Найдем значение коэффициента к
2к – 1,5 = -5
2к = - 5 + 1,5
2к = - 3,5 | : 2
к = - 1,75
Значит функция имеет вид f(x) = -1,75х – 1,5
f(x) = -1,75х – 1,5
-1,75х – 1,5 = 16
x = - 10
Ответ: х=-10

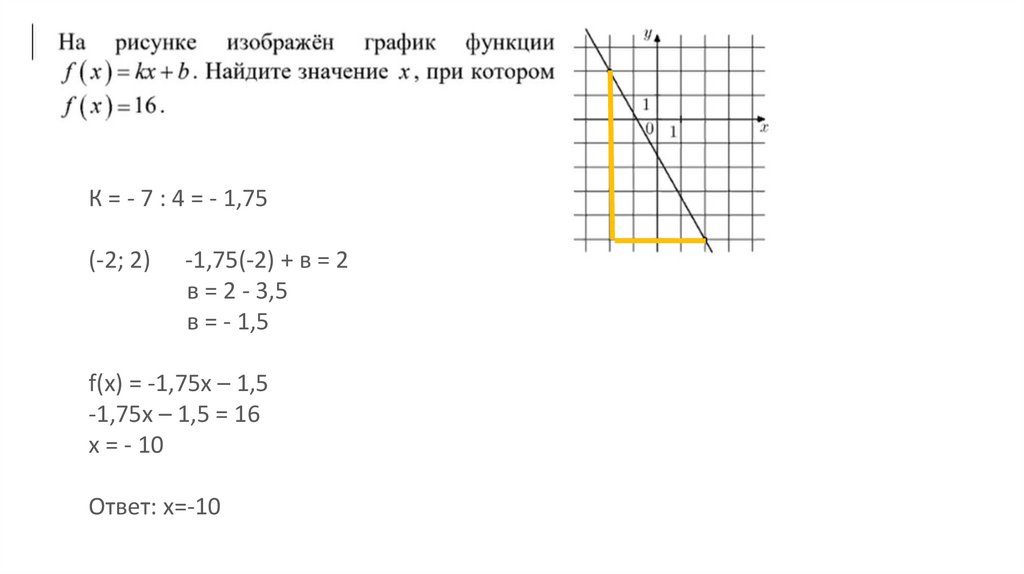
9.

К = - 7 : 4 = - 1,75
(-2; 2)
-1,75(-2) + в = 2
в = 2 - 3,5
в = - 1,5
f(x) = -1,75х – 1,5
-1,75х – 1,5 = 16
x = - 10
Ответ: х=-10

10.

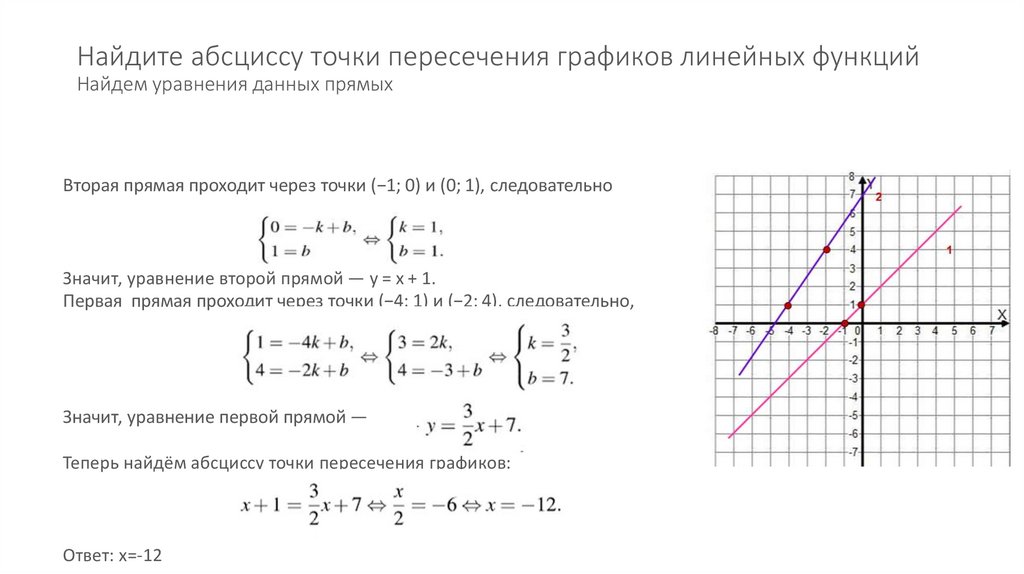
Найдите абсциссу точки пересечения графиков линейных функций
Найдем уравнения данных прямых
Вторая прямая проходит через точки (−1; 0) и (0; 1), следовательно
Значит, уравнение второй прямой — y = x + 1.
Первая прямая проходит через точки (−4; 1) и (−2; 4), следовательно,
Значит, уравнение первой прямой —
Теперь найдём абсциссу точки пересечения графиков:
Ответ: х=-12

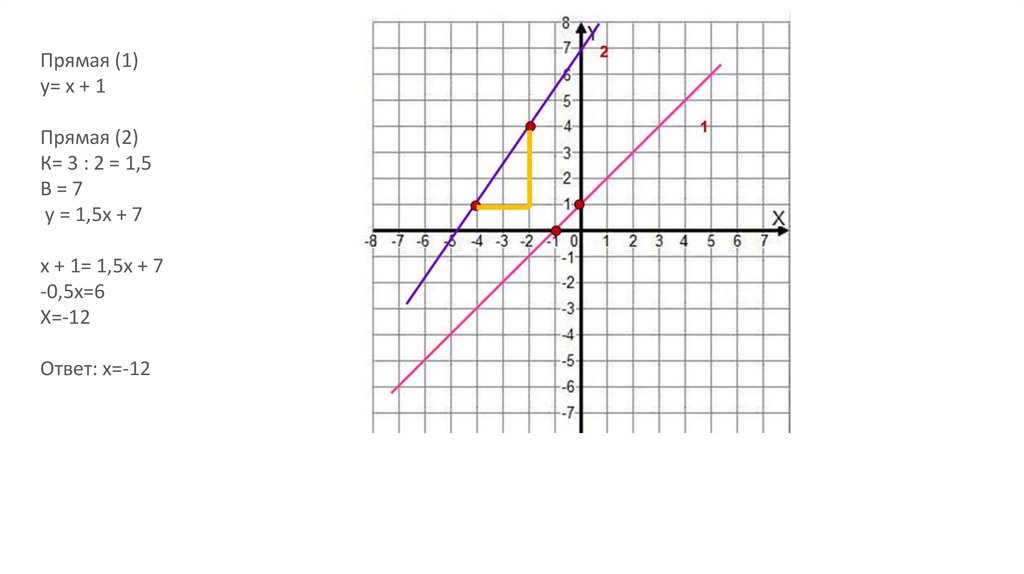
11.

Прямая (1)
у= х + 1
Прямая (2)
К= 3 : 2 = 1,5
В=7
у = 1,5х + 7
х + 1= 1,5х + 7
-0,5х=6
Х=-12
Ответ: х=-12

12.

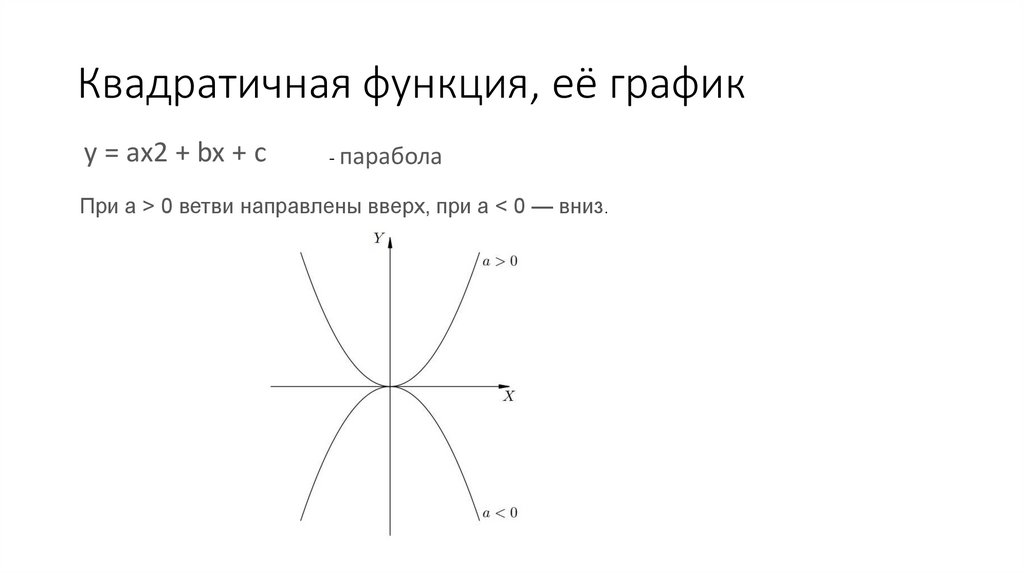
Квадратичная функция, её график
y = ax2 + bx + c
- парабола
При a > 0 ветви направлены вверх, при a < 0 — вниз.

13.

Абсцисса вершины параболы y = ax2 + bx + c находится по формуле:
Для нахождения ординаты вершины y0 удобнее всего подставить x0 в
уравнение параболы
или по формуле
Точки пересечения параболы y = ax2 + bx + c с осью X находятся с
помощью решения квадратного уравнения ax2 + bx + c = 0. Если
дискриминант равен нулю, то парабола касается оси X. Если
дискриминант меньше нуля, то парабола не пересекает ось X.
Точка пересечения с осью Y находится легко: мы просто подставляем x = 0
в уравнение параболы. Получается точка (0, c).

14.

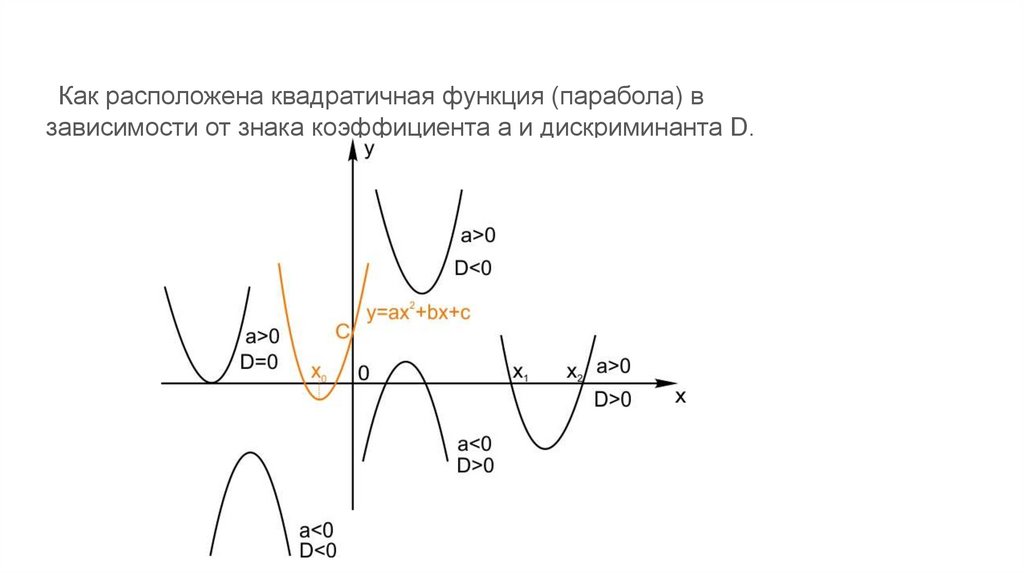
Как расположена квадратичная функция (парабола) в
зависимости от знака коэффициента а и дискриминанта D.

15.

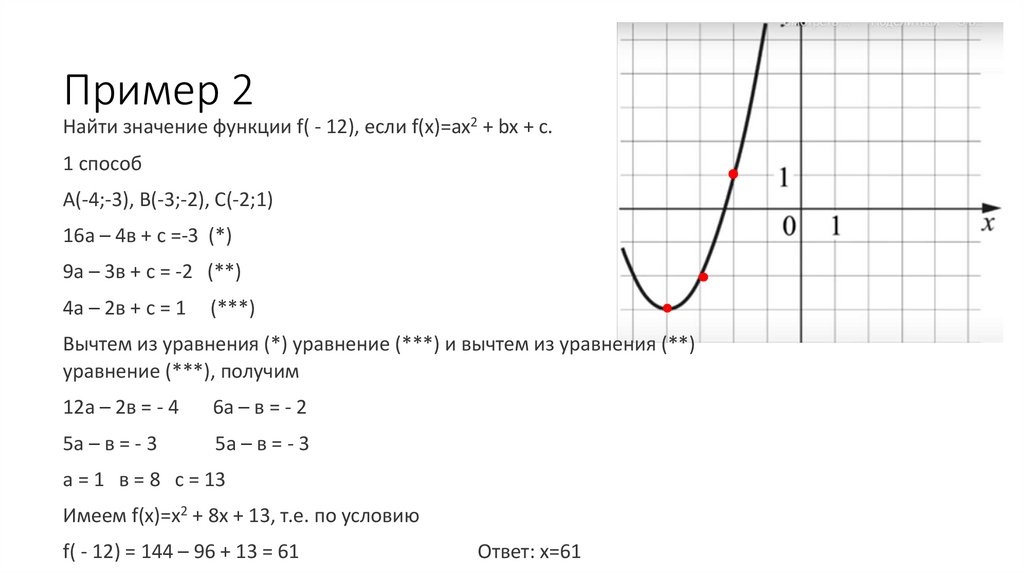
Пример 2
Найти значение функции f( - 12), если f(x)=ax2 + bx + c.
1 способ
А(-4;-3), В(-3;-2), С(-2;1)
16а – 4в + с =-3 (*)
9а – 3в + с = -2 (**)
4а – 2в + с = 1
(***)
Вычтем из уравнения (*) уравнение (***) и вычтем из уравнения (**)
уравнение (***), получим
12а – 2в = - 4
6а – в = - 2
5а – в = - 3
5а – в = - 3
а = 1 в = 8 с = 13
Имеем f(x)=x2 + 8x + 13, т.е. по условию
f( - 12) = 144 – 96 + 13 = 61
Ответ: х=61

16.

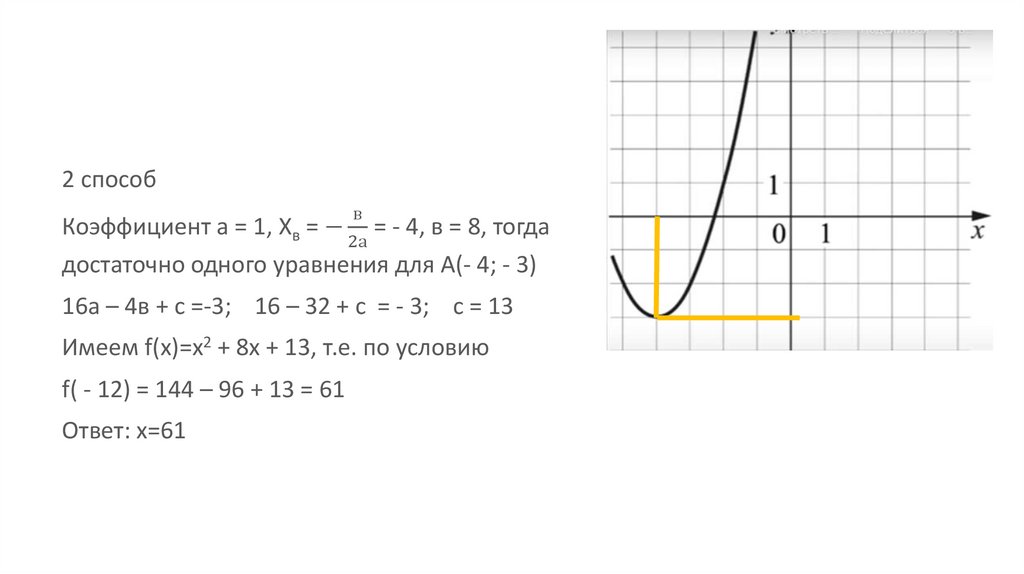
2 способ
в
Коэффициент а = 1, Хв = − = - 4, в = 8, тогда
2а
достаточно одного уравнения для А(- 4; - 3)
16а – 4в + с =-3; 16 – 32 + с = - 3; с = 13
Имеем f(x)=x2 + 8x + 13, т.е. по условию
f( - 12) = 144 – 96 + 13 = 61
Ответ: х=61

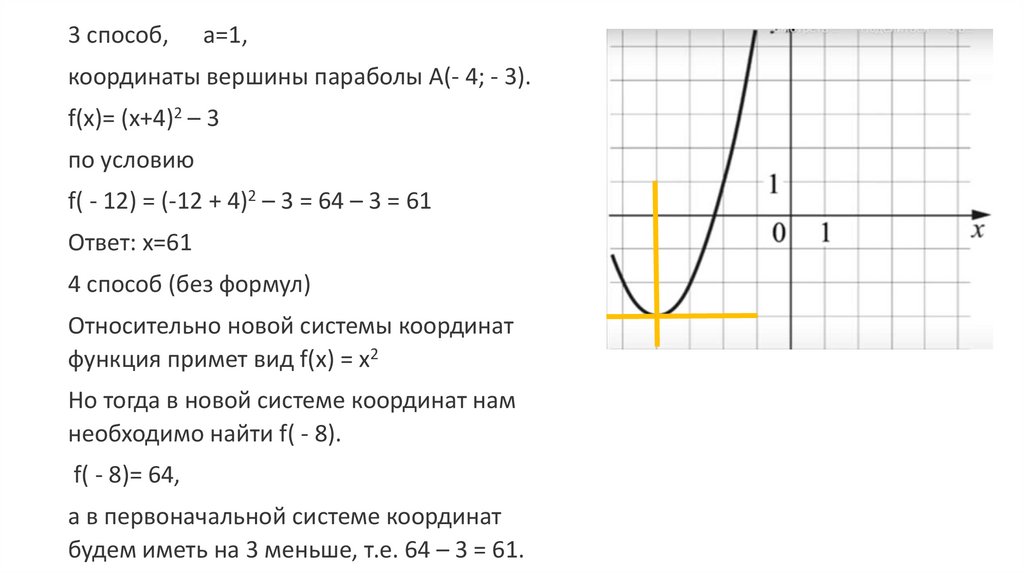
17.

3 способ,
а=1,
координаты вершины параболы А(- 4; - 3).
f(x)= (x+4)2 – 3
по условию
f( - 12) = (-12 + 4)2 – 3 = 64 – 3 = 61
Ответ: х=61
4 способ (без формул)
Относительно новой системы координат
функция примет вид f(x) = x2
Но тогда в новой системе координат нам
необходимо найти f( - 8).
f( - 8)= 64,
а в первоначальной системе координат
будем иметь на 3 меньше, т.е. 64 – 3 = 61.

18.

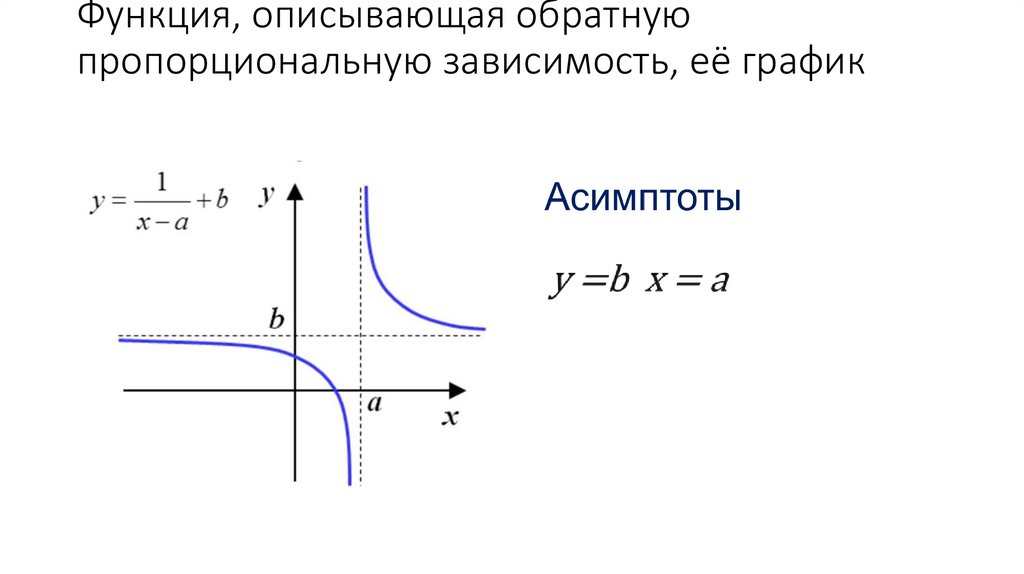
Функция, описывающая обратную
пропорциональную зависимость, её график

19.

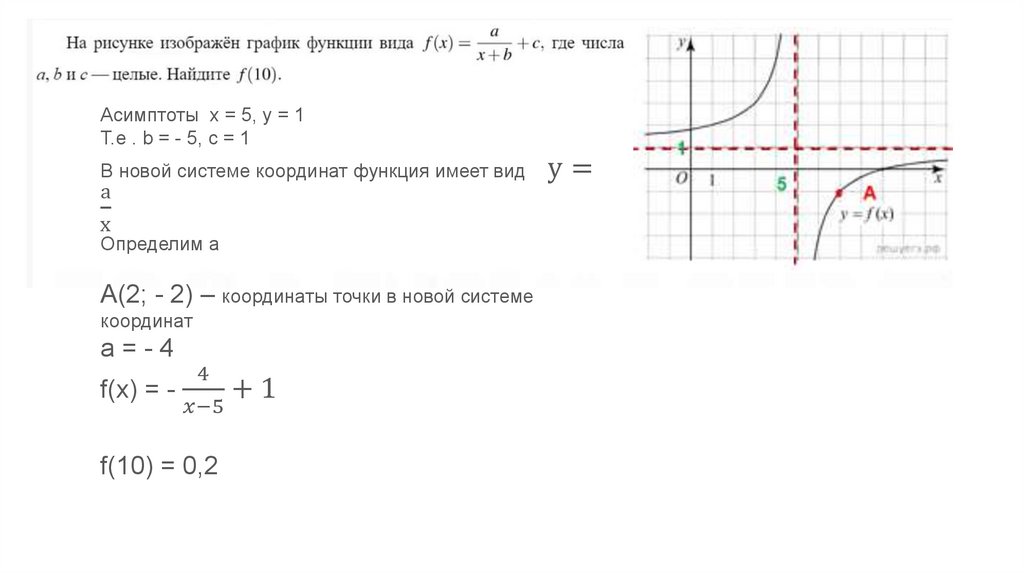
Асимптоты х = 5, у = 1
Т.е . b = - 5, c = 1
В новой системе координат функция имеет вид
а
х
Определим а
А(2; - 2) – координаты точки в новой системе
координат
а=-4
4
f(x) = +1