Санды теңдіктер және олардың қасиеттері (6 сынып)

1. Санды теңдіктер

• Сабақтың тақырыбы:
6 сынып
«Санды теңдіктер және олардың
қасиеттері»
• Оқу бағдарламасына сәйкес оқыту мақсаттары:
• 6.2.2.1
• тура санды теңдіктердің қасиеттерін білу және
қолдану;

2.

• Өзара тең екі санды өрнектің
теңдік «=» белгісімен
жазылуы санды теңдік деп
аталады.
• Мысалы, санды теңдіктер:
• 5 = 5,
• 36 ÷ 3 + 4 = 16.
т.б.

3.

Өзара тең екі санды өрнектің теңдік «=»
белгісімен жазылуы санды теңдік деп
аталады.
№1. Мысалы,
36=12 ∙ 3 және
12 ∙ 3=9 ∙ 4
болса, онда
36 = 9 ∙ 4.
№2. Мысалы:
3 + 4 = 7,
3 + (–2) + 4 = 7 + (–2),
5 = 5.

4.

5.

Тура санды теңдіктің екі бөлігіне
де
22 - 6 = 24 - 8
бірдей 8 санын қосыңыз.
Сіз не байқайсыз?

6. 2-қасиет

Егер тура санды теңдіктің екі
жағына да бірдей санды
көбейтсек, содан кейін де біз тура
санды теңдікті аламыз
егер a= b ,онда a · c = b · c
Мына тура санды теңдіктің
22 - 6 = 24 – 8 екі жағына да 2
санын көбейтіп көр. Не
байқадыңыз?

7. 3 қасиет

Мына тура екі теңдіктің қайсысы
22 – 9 = 24 – 11 және 24 – 11 = 45 – 32
Келесі тура теңдікке тең
22 – 9 = 45 – 32 ?
Егер a= b және b =
болса,
онда a = c

8. 4 қасиет

егер a= b , с = d ,
онда a+c = b+d орныдалады
Тура Теңдіктердің оң жағын оң
жаңына , сол жағын сол
жағына қосыныздар
67 – 62 = 5 және 12 – 7 = 13 – 8
Не байқадыңыздар?

9. 5 қасиет

Тура санды теңдіктердің оң
жағын оң жаңына , сол жағын
сол жағына көбейтсек тура
санды теңдік шығады.
егер a= b , с = d тура санды
теңдіктер ,
онда a · c = b · d

10. тапсырма

Тура санды теңдіктер қасиеттерін пайдаланып,
тура санды теңдіктер жазыңыздар.
А) 0,5 +… = 1/2+ …
Б) 0,75 · …
= ¾·…
С) 3,5 – 0,5 = 7,25 – 4,25 және
7,25 – 4,25 = 15 : 5 ,
онда…..

11. тапсырма

Тура санды теңдіктер қасиеттерін пайдаланып,
тура санды теңдіктер жазыңыздар.
Д) 10,2 – 0,2 = 30,5 – 20,5 және
0,8 + 0,2 = 11 – 1, онда……
Е) 2,2 + 2,3 = 9 – 3,5 және
9,9 – 9,8 = 54,3 – 54,2 , онда…..

12. Өзіндік жұмыс!

№
5а = 15 және 3b = 6
Тура санды теңдіктер
екені белгілі
2а = 10 және 4b = 8
Тура санды теңдіктер
екені белгілі
1
Екі жағына да 2 санын
қосыңыз:
Екі жағына да -2 санын
қосыңыз
2
Екі жағына да 2 санын
көбейтіңіз:
Екі жағына да -2 санын
көбейтіңіз:
3
Мүшелеп қосып көріңіз
Мүшелеп қосып кқріңіз:
4
Мүшелеп көбейтіп кқріңіз
(оң жағын оң жағына, сол
жағын сол жағына)
Мүшелеп көбейтіңіз (оң жағын
оң жағына, сол жағын сол
жағына)

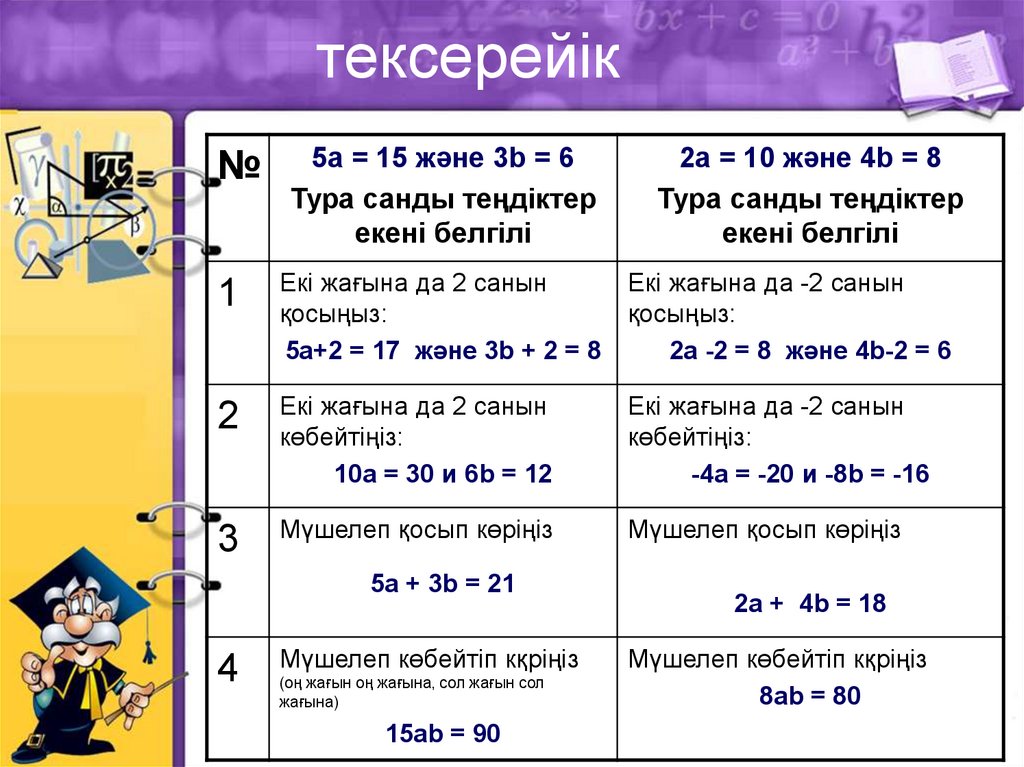
13. тексерейік

№
5а = 15 және 3b = 6
Тура санды теңдіктер
екені белгілі
2а = 10 және 4b = 8
Тура санды теңдіктер
екені белгілі
1
Екі жағына да 2 санын
қосыңыз:
5а+2 = 17 және 3b + 2 = 8
Екі жағына да -2 санын
қосыңыз:
2а -2 = 8 және 4b-2 = 6
2
Екі жағына да 2 санын
көбейтіңіз:
10а = 30 и 6b = 12
Екі жағына да -2 санын
көбейтіңіз:
-4а = -20 и -8b = -16
3
Мүшелеп қосып көріңіз
Мүшелеп қосып көріңіз
5а + 3b = 21
4
Мүшелеп көбейтіп кқріңіз
(оң жағын оң жағына, сол жағын сол
жағына)
15аb = 90
2а + 4b = 18
Мүшелеп көбейтіп кқріңіз
8аb = 80

14.

15.

№767. Тура санды теңдіктің қасиетін
пайдаланып,
1) 1,2·(-7)=-8,4 теңдігінің екі жақ бөлігін де:
а) -5-ке; ә) 3-ке; б) 0,5-ке көбейтіңдер;
2) 5,4·2=10,8 теңдігінің екі жақ бөлігін де:
а) -3-ке; ә) 9-ға; б) 6-ға бөліңдер.

16.

17.

В деңгейі
№769. Тура санды теңдік шарты
орындалатындай етіп, жақшаны қойыңдар:
1) 2-8·0,5=48:(-16);
2) 72:9+3=3,2+2,8;
3) 9,6:1,2=5·0,7+0,9 4) 9·2-8=20·(-2,7)
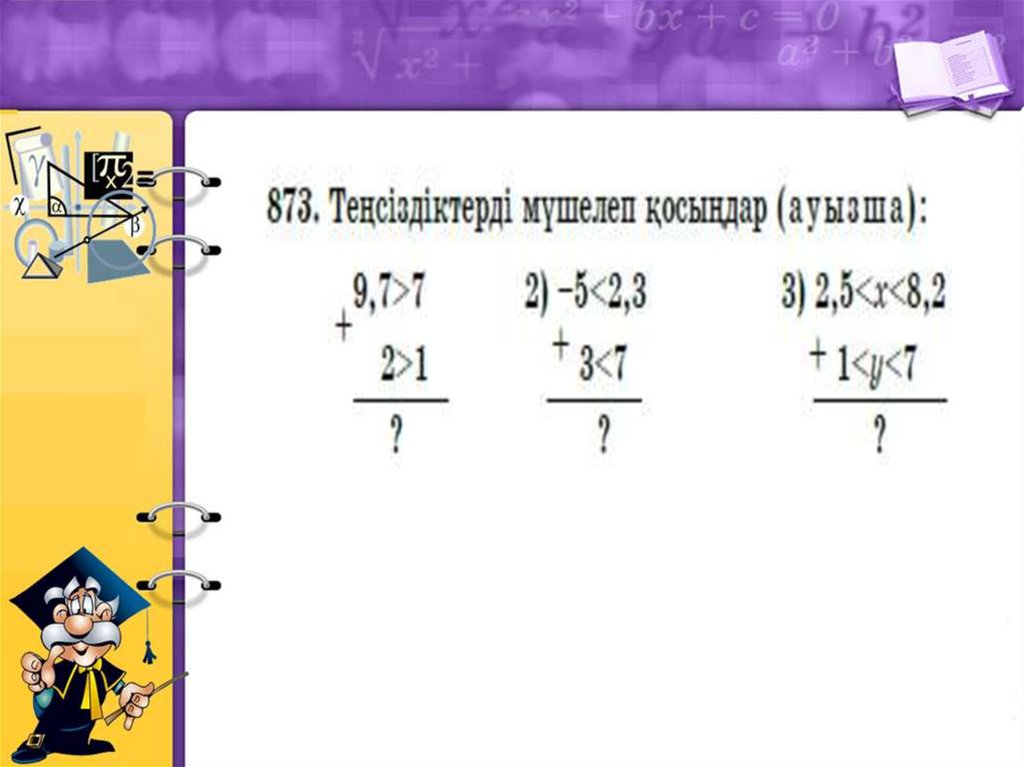
№770. Тура санды теңдіктерді мүшелеп қосуды
орындаңдар:
0,6-2=-1,4 және
2+1,8=3,8
1,7+6=7,7 және 0,5-1,7=0,4·(-3)
1,8·(-5)=-2·4,5 және -5·1,2=-2·3

18.

С деңгейі
№773. Тура санды теңдіктердің a = b, b = c, a = c
қасиеттерін пайдаланып, берілген өрнектерден үш
тура санды теңдік құрастырыңдар:
32 8;
14,4 : 0,2;
100 – 28;
15 1,4;
23 + 13;
8,4 : 0,4;
2,5 12;
4,5 : 0,15;
8 3 + 6.

19.

20.

.3 -4 сабақ
Сабақтың тақырыбы:
Бір айнымалысы бар
сызықтық
теңдеулерді шешу
6.2.2.2
бір айнымалысы бар сызықтық теңдеудің,
мәндес теңдеулердің анықтамаларын білу;

21.

22.

1. Берілген теңдеуге мәндес теңдеу жазыңдар:
а) x – 7 = 5;
b) 2x – 4 = 0;
c) x – 11 = x – 7;
d) 2(x – 12) = 2x – 24.
2. Мына теңдеулер мәндес пе: 3х+2х=15 және 5х=5?
(жоқ)
3. 7 саны мына теңдеудің түбірі бола ма: 3х-6=х+8? (ия)

23.

Тапсырма.1. Төменде берілген
үш теңдеудің ішінен мәндес
теңдеулерді табыңыз және
жауаптарыңызды негіздеңіз:

24.

25.

26.

27.

28.

29.

30.

31.

32.

Сабақтың тақырыбы:
.5 сабак
Бір айнымалысы бар
сызықтық
теңдеулерді шешу
6.2.2.3
бір айнымалысы бар сызықтық теңдеулерді
шешу;

33.

34.

35.

36.

37.

38.

39.

40.

Үйге №

41.

Сабақтың тақырыбы:
6 сабак
Бір айнымалысы бар
сызықтық
теңдеулерді шешу
6.2.2.3
бір айнымалысы бар сызықтық теңдеулерді
шешу;

42.

43.

44.

45.

«Есепті аяқта!» - оқушылардың тез есептеу қабілеттерін,
шапшандықтарын дамыту.

46.

47.

48.

Үйге №

49.

Сабақтың тақырыбы:
7-8 сабак
Бір айнымалысы бар
сызықтық
теңдеулерді шешу
6.2.2.3
бір айнымалысы бар сызықтық теңдеулерді
шешу;

50.

«Ой қозғау»
С-1: Қандай теңдеуді бір айнымалысы бар теңдеу деп
атайды?
С-2: Мәндес теңдеу деп қандай теңдеуді айтады?
С-3: Теңдеудің қандай қасиеттері бар?
С-4: Бір айнымалысы бар теңдеуді шешу алгоритмін атаңдар
С-5: ах=b түріндегі теңдеуді шешудің неше жағдайы бар?
ax = b түріндегі теңдеу бір айнымалысы бар сызықтық
теңдеу деп аталады, мұндағы x – айнымалы, a және b –
қандай да бір сандар.
Теңдеуді шешу деп айнымылының орнына қойғанда дұрыс
санды теңдікке айналдыратын x (теңдеудің түбірі) белгісіз
айнымалысының барлық мәнін табуды айтады.
Теңдеуді шешу кезінде жақшаларды ашу, ұқсас мүшелерді
біріктіру, өрнекті ықшамдау амалдары орындалады. Бірақ
ықшамдалған кезде теңдеу мәндес теңдеуге түрленеді.
Түбірлері бірдей теңдеулерді мәндес теңдеу деп атайды

51.

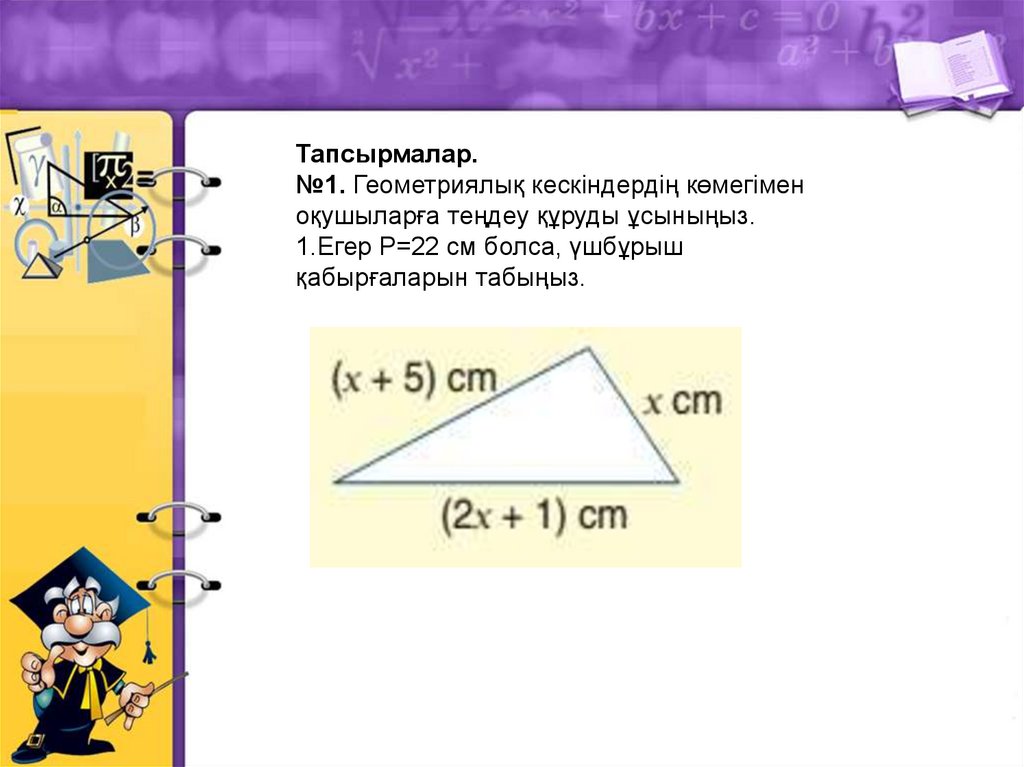
Тапсырмалар.
№1. Геометриялық кескіндердің көмегімен
оқушыларға теңдеу құруды ұсыныңыз.
1.Егер Р=22 см болса, үшбұрыш
қабырғаларын табыңыз.

52.

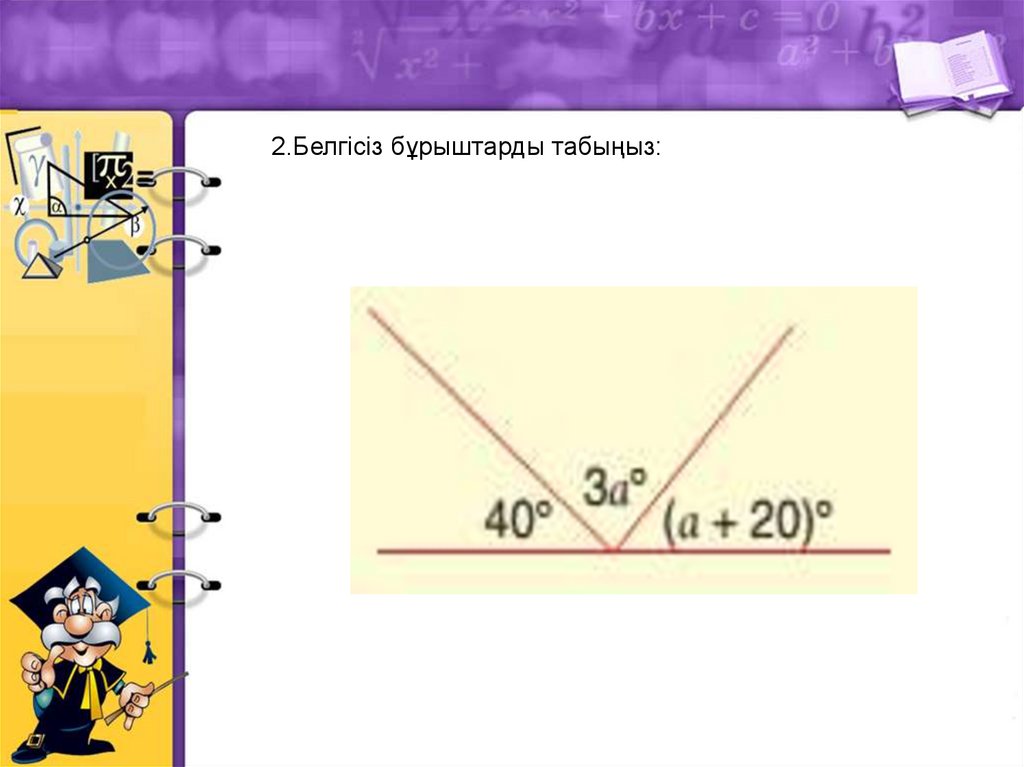
2.Белгісіз бұрыштарды табыңыз:

53.

А деңгейі. №1.
2x+17=22+3x;
18+3x=x+14;
25-4x=12-5x;
13х + 27 = 16x + 4,5.

54.

55.

56.

815. Ұзындығы 12 см тік төртбұрыш және қабырғасы осы тік
төртбұрыштың енінен 1 см кем квадрат берілген. Квадраттың периметрі
берілген
тік төртбұрыштың периметрінен 10 см кем. Тік төртбұрыштың
ені неше
сантиметр?
816. Елді мекен стансыдан 4 км қашықтықта станcы мен саяжай
аралығында орналасқан. Елді мекеннен саяжайға қарай 75
м/мин
жылдамдықпен жаяу адам шықты. Жаяу адам 0,5 сағ жүрген
соң стансыдан 200 м/мин жылдамдықпен велосипедші шықты.
Велосипедші неше минут жүрген соң жаяу адамды қуып жетеді?
817. Домбыра үйірмесіне қатысуға тілек білдірушілердің
1\5-іі домбыра тарта біледі. Қалғандары домбыра тарта
білмейді. Бір апта ішіндедомбыра тарта білмейтіндердің 6-уы
домбыра тартуды үйренгенде,үйірмеге қатысушылардың 10%-і
ғана домбыра тарта білмейтін болды. Домбыра үйірмесіне
қатысушылардың саны нешеу?
А. 20; В. 24; С. 25; D. 18.

57.

Үйге №

58.

Сабақтың тақырыбы:
9 сабак
Айнымалысы модуль таңбасының ішінде
берілген бір айнымалысы бар сызықтық
теңдеу
6.2.2.4
|х+-а|=b түріндегі теңдеулерді шешу, мұндағы
a және b – рационал сандар

59.

60.

61.

62.

63.

64.

65.

66.

Үйге №

67.

Сабақтың тақырыбы:
10 сабак
Айнымалысы модуль таңбасының ішінде
берілген бір айнымалысы бар сызықтық
теңдеу
6.2.2.4
|х+-а|=b түріндегі теңдеулерді шешу, мұндағы
a және b – рационал сандар

68.

«Миға шабуыл» өткен сабақ бойынша қайталау сұрақтары:
С-1: Айнымалысы модуль таңбасының ішінде берілген бір
айнымалысы бар сызықтық теңдеу дегеніміз не, оған мысал
келтір.
С-2: Айнымалысы модуль таңбасының ішінде берілген бір
айнымалысы бар сызықтық теңдеуді шешуде қандай ережелерді
және формулаларды пайдаланамыз?
С-3: Айнымалысы модуль таңбасының ішінде берілген бір
айнымалысы бар сызықтық теңдеуді шешудің неше тәсілін
қарастырдық?
С-4: Айнымалысы модуль таңбасының ішінде берілген бір
айнымалысы бар сызықтық теңдеуді шешудің бірінші тәсілі
қандай, мысал келтір.
С-5: Айнымалысы модуль таңбасының ішінде берілген бір
айнымалысы бар сызықтық теңдеуді шешудің екінші тәсілі
қандай, мысал келтір.

69.

70.

71.

Үйге №

72.

Сабақтың тақырыбы:
11 сабак
Айнымалысы модуль таңбасының ішінде
берілген бір айнымалысы бар сызықтық
теңдеу
6.2.2.4
|х+-а|=b түріндегі теңдеулерді шешу, мұндағы
a және b – рационал сандар

73.

74.

75.

76.

77.

78.

79.

Үйге №

80.

Сабақтың тақырыбы:
Теңдеулер көмегімен мәтінді
есептерді шығару
6.5.1.6 мәтінді есептерді сызықтық
теңдеулерді құру арқылы шығару;

81.

«Ой қозғау»
С-1: Қандай теңдеуді бір айнымалысы бар теңдеу деп
атайды?
С-2: Мәндес теңдеу деп қандай теңдеуді айтады?
С-3: Теңдеудің қандай қасиеттері бар?
С-4: Бір айнымалысы бар теңдеуді шешу алгоритмін
атаңдар
С-5: ах=b түріндегі теңдеуді шешудің неше жағдайы бар?
«Білім таусылмайтын кен» (тест тапсырмасы)
1. Теңдеуді шешу:
0х=5
а) 0;
в) 5;
с) түбірі жоқ
2. Теңдеуді шешу:
7х+3 = х+15
а) 2,25;
в) 2;
с) 3
3. Теңдеуді шешу:
0х = 0
а) 0;
в) 1;
с) х- кез-келген сан
4. Теңдеуді шешу:
6х-7 = х+3
а) 2;
в) -4/7
с) -4
5. Теңдеуді шешу:
3х = 1
а) 3;
в) 1/3
с)

82.

83.

Сызықтық теңдеу құруға және оның түбірін табуға арналған
өзіндік жұмыстар
№1 тапсырма.
Суреттегі таразының сол жақ табақшасына 3 пакет ұн, ал оң жақ
табақшасына 1 пакет ұн және 4 кг кіртасы салынған.
Сурет бойынша сызықтық теңдеу құрыңдар, мұндағы 1 пакет ұнның
массасы х кг.
Теңдеуді шешіп, 1 пакет ұнның массасын анықтаңдар.
№2 тапсырма.
Суреттегі таразының сол жақ табақшасына массалары бірдей 5 орамжапырақ және 500 г кіртасы, ал оң жақ табақшасына 2 орамжапырақ
және 2 кг кіртасы салынған.

84.

№3 тапсырма.
Суретте таразының сол жақ табақшасында 4 бөлек шай және 50 г
кіртасы, ал оң жақ табақшасында 1 бөлек шай және 500 г кіртасы
кескінделген.
Сурет бойынша теңдеу құрыңдар, мұндағы 1 бөлек шайдың массасы
х г. Теңдеуді шешіп, 1 бөлек шайдың массасын табыңдар.
№4 тапсырма.
Суретте таразының сол жақ табақшасында бал құйылған ыдыс және
500 г кіртасы, оң жақ табақшасында бос ыдыс және 2 кг, 1 кг кіртастары
кескінделген. Бал құйылмай тұрғандағы ыдыс пен бос ыдыстың массалары тең.

85.

Сабақтың тақырыбы:
Санды теңсіздіктер және
олардың қасиеттері
6.2.2.5 тура санды теңсіздіктердің қасиеттерін
білу және қолдану;
6.2.2.6 теңсіздіктерді қосу, азайту, көбейту
және бөлуді түсіну және қолдану;

86.

Есеп. Ұзындығы 7 см, ені 4 см тік
төртбұрыштың ауданын қабырғасы
5 см квадраттың ауданымен
салыстырыңдар. Салыстыру нәтижесін
теңсіздік түрінде жазыңдар.
Шешуі. 7 · 4 – тік төртбұрышының ауданы.
52– квадраттың ауданы.
7 · 4 > 52 – санды теңсіздік.
Екі санды өрнектің теңсіздік белгісімен
(«>» немесе «<») жазылуы санды теңсіздік деп аталады.
Теңсіздік белгісінің сол жағындағы жазуды
теңсіздіктің сол жақ
бөлігі деп, ал оң жағындағы жазуды
теңсіздіктің оң жақ бөлігі деп атайды

87.

88.

1. Сан аралығының неше түрі бар?
2. ( 2; 7 ) сан аралығының оқылуы және сан
аралығының аты қалай?
3. Бір айнымалысы бар сызықтық теңсіздік дегеніміз не?
4. [-3;5] және [1;9] сан аралығының қиылысуын табыңдар.

89.

90.

851. Координаталық түзуде А, В және С
нүктелері берілген (5.1-сурет).
1) А нүктесі мен В нүктесінің; 2) В
нүктесі мен С нүктесінің;
3) А нүктесі мен С нүктесінің
координатасын салыстырып, нәтижесін
санды теңсіздік түрінде жазыңдар

91.

852. Теңсіздік түрінде жазыңдар. Белгісіз шаманы х-пен
белгілеңдер:
1. Ыдыстағы сұйықтың көлемі 3 л-ден артық емес;
2. Өзен суының ағыс жылдамдығы 4 км/сағ-тан кем;
3. Бүгін Тараз қаласындағы ауаның температурасы 5°Стан төмен
емес.
4. Доғал бұрыштың градустық өлшемі 90°-тан артық,
бірақ 180°-тан кем.

92.

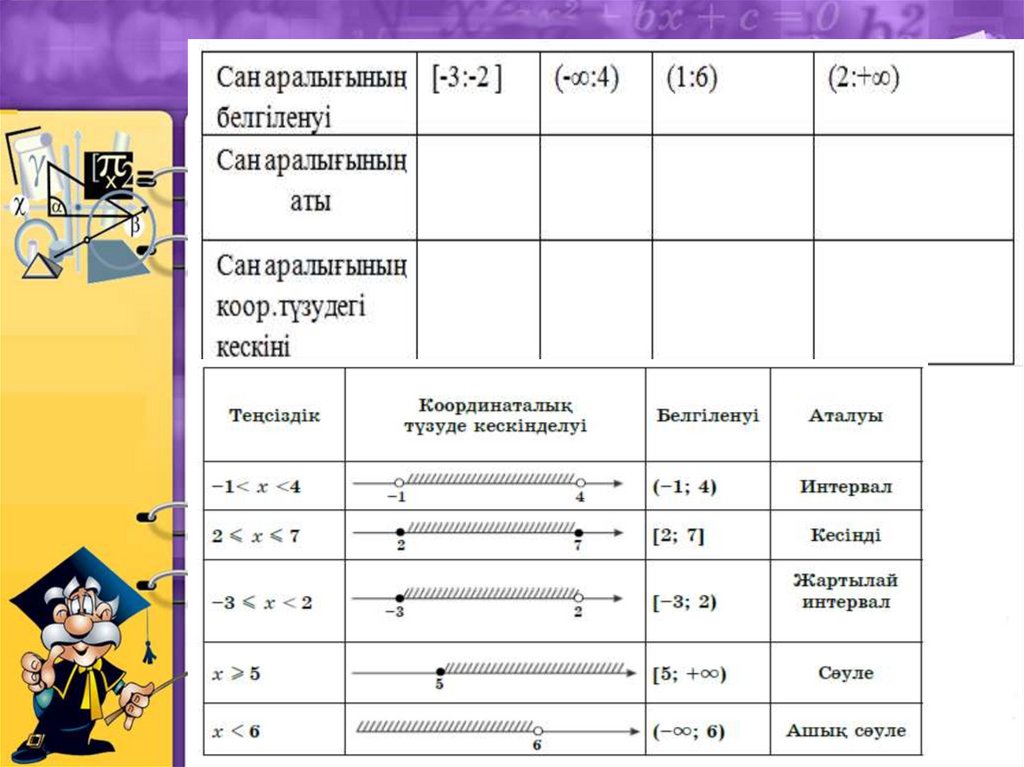
853. Жұлдызшаның (*) орнына тиісінше >
немесе < белгілерін жазып,
тура санды теңсіздік құрастырыңдар. Кестені
толтырыңдар:

93.

94.

95.

96.

97.

98.

99.

100.

101.

102.

103.

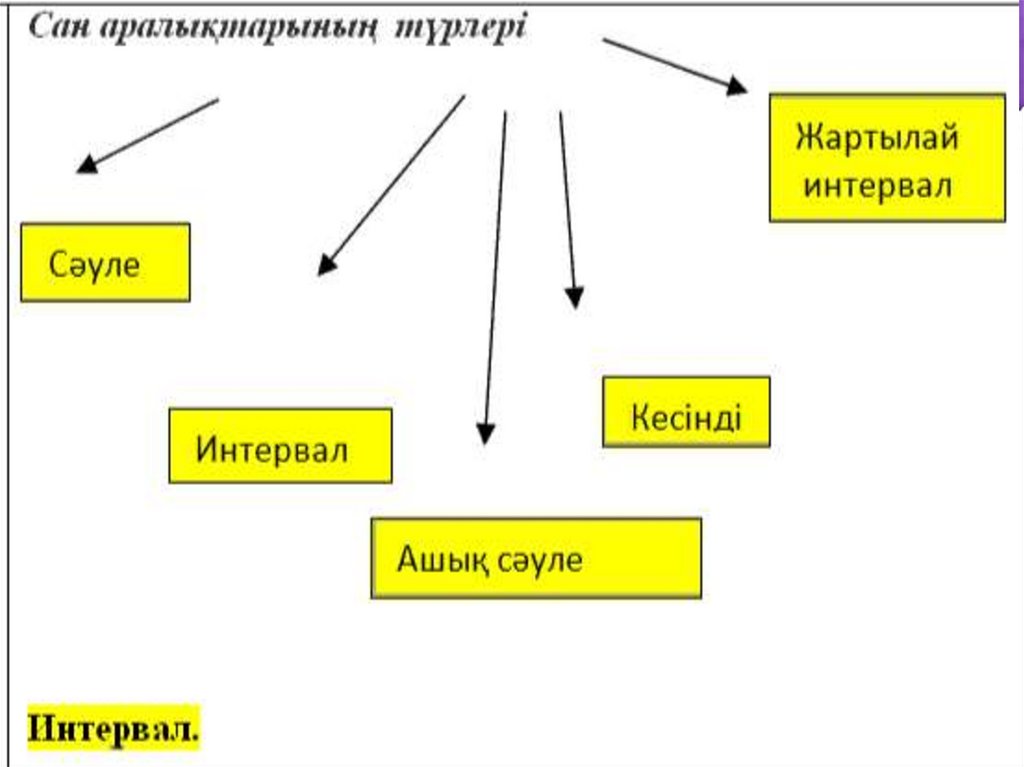
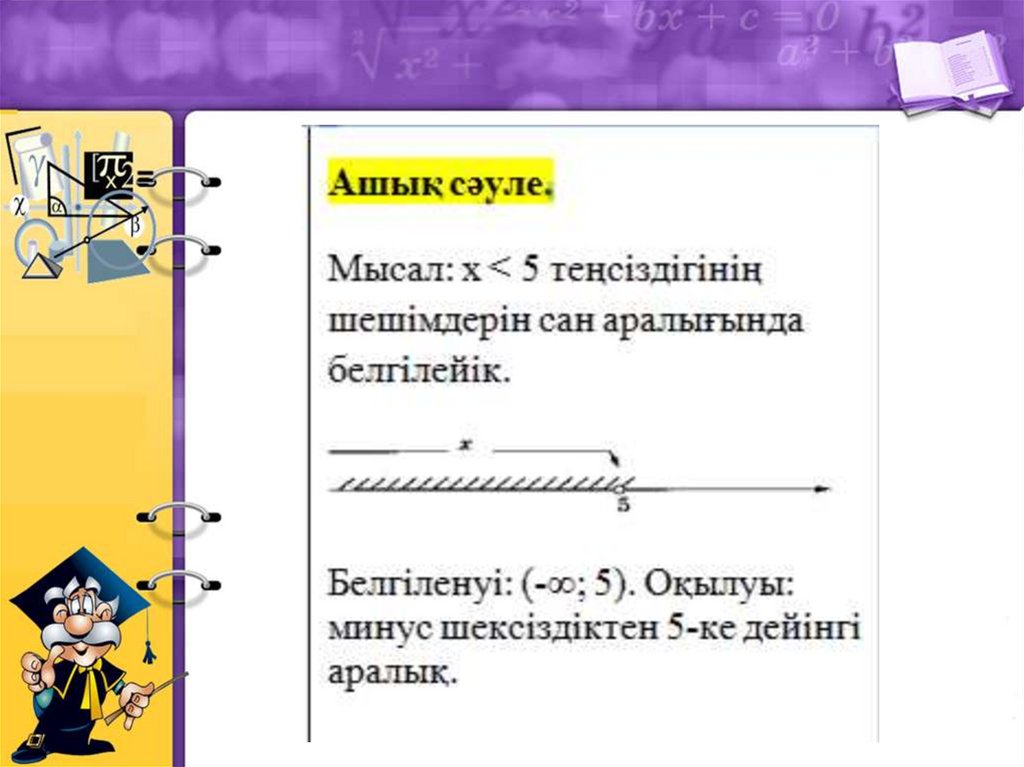
Сабақтың тақырыбы:
Сан аралықтар. Сан
аралықтардың бірігуі мен
қиылысуы
6.2.2.7 сан аралықтарын жазу үшін
белгілеулерді пайдалану;
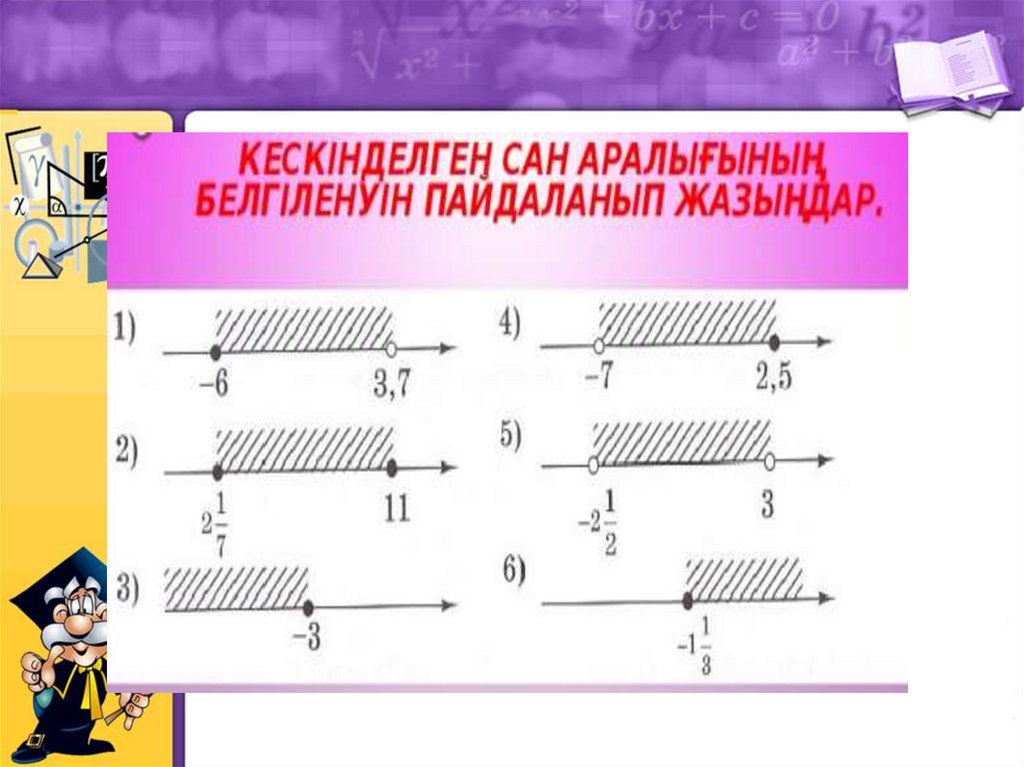
6.2.2.8 сан аралықтарды кескіндеу;

104.

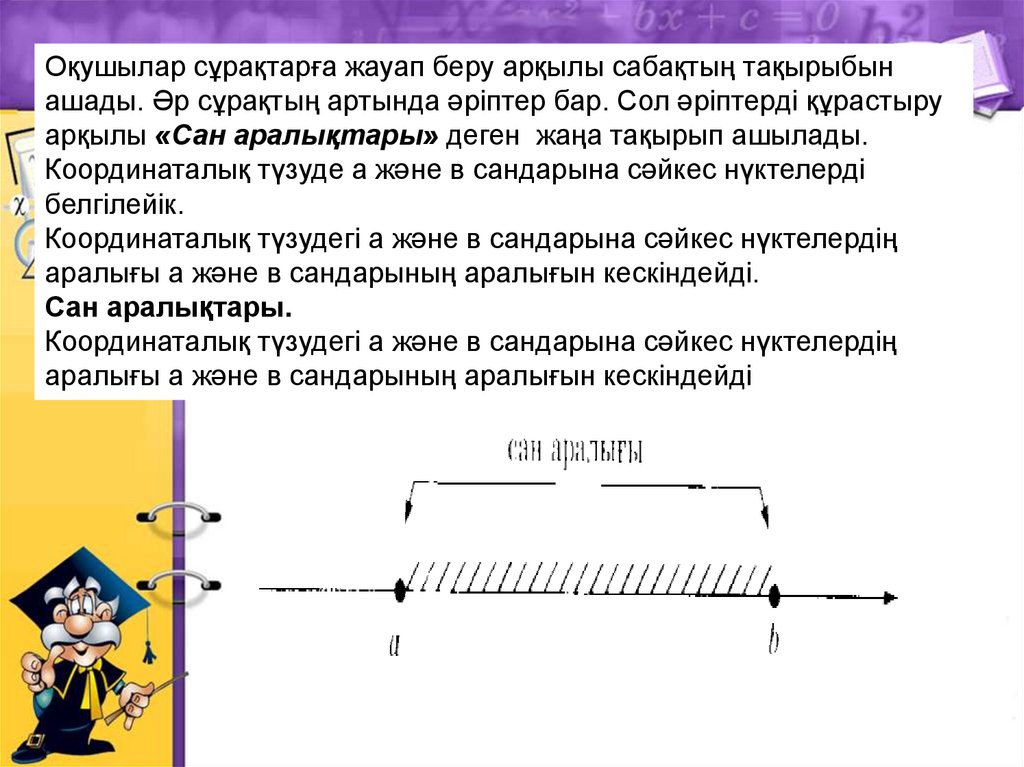
Оқушылар сұрақтарға жауап беру арқылы сабақтың тақырыбын
ашады. Әр сұрақтың артында әріптер бар. Сол әріптерді құрастыру
арқылы «Сан аралықтары» деген жаңа тақырып ашылады.
Координаталық түзуде а және в сандарына сәйкес нүктелерді
белгілейік.
Координаталық түзудегі а және в сандарына сәйкес нүктелердің
аралығы а және в сандарының аралығын кескіндейді.
Сан аралықтары.
Координаталық түзудегі а және в сандарына сәйкес нүктелердің
аралығы а және в сандарының аралығын кескіндейді

105.

106.

107.

108.

109.

110.

111.

Өткен сабақты бекіту үшін: “ Қағып ал”
1.Санды теңсіздік дегеніміз не?
2. Координаталық түзуде үлкен сан кіші санның қай
жағында кескінделеді?
3. Санды теңсіздіктің бір жақ бөлігін оның екінші жақ
бөлігіне орын ауыстырғанда теңсіздік белгісі қалай
өзгереді?
4. Қандай теңсіздіктерді мүшелеп қосып болады?
5. Қандай теңсіздіктерді мүшелеп алуға болады?
6. Айырма теңсіздіктің теңсіздік белгісі қалай анықталады?
7. Қандай теңсіздіктерді көбейтуге болады?
8. Теңсіздік белгілері бірдей теңсіздіктер қалай көбейтіледі?
9. Теңсіздіктер қалай бөлінеді?
10. Санды теңсіздіктің екі жақ бөлігін де бірдей теріс санға
көбейтсек немесе бөлсек, теңсіздік белгісін қалай өзгерту
керек?
11. 1 теңсіздігіндегі х-тің теңсіздік тура болатын сан
мәндерін табыңдар.
12. 1 координаталық тузуде белгілеңіз.
13. -2 теңсіздігіндегі х-тің мәндерін табыңдар.

112.

113.

114.

Сан аралықтарының қиылысуындағы ең
үлкен бүтін санды
көрсетіңдер:
1) (–8; 6] және [–5; 8); 4) (–4; 2) және (–7; –1);
2) (–∞; 0] және [–9; 3); 5) [–9; 9] және [–1; 14];
3) (–∞; –2] және [–2; 7]; 6) (–6; 6) және [–4; 4].
932. . Сан аралықтарын координаталық
түзуде кескіндеңдер;
. Сан аралықтарының бірігуін тауып, оны
белгіленуімен жазыңдар;
. Сан аралықтарының бірігуіндегі ең кіші бүтін
санды көрсетіңдер:
1) [–8; 2] және [1; 9); 4) (–11; 3] және [–2; 7);
2) (–6; 7) және (–2; 4); 5) [–7,5; –3] және [0; 4];