Элементы математической статистики

1. Статистические методы обработки и анализа управленческой информации

«Почему дует ветер? – Потому что
деревья качаются».
О.Генри

2. Тема 2.2. Элементы математической статистики

Лекции 5, 6
Попова Е.Э.

3. Гипотезы о параметрах распределения

Пример: Гипотеза о равенстве вероятности числу.
Фирма рассылает рекламные каталоги
возможным заказчикам. Как показал опыт,
вероятность того, что организация получившая
каталог, закажет рекламируемое изделие,
равна 0,08. Фирма разослала 1000 каталогов
новой, улучшенной, формы и получила 100
заказов. На уровне значимости 0,05 выяснить,
можно ли считать, что новая форма рекламы
существенно лучше прежней.

4. Гипотезы о параметрах распределения

Пример: Гипотеза о равенстве вероятности числу.
H0 : p = 0,08
H1 : p > 0,08
Фпракт=2,33
Фтеор=1,65
Новая форма рекламы значимо эффективнее
прежней.

5. Гипотезы о параметрах распределения

Пример: Гипотеза о равенстве вероятностей
Выборочная проверка надежности материнских
плат 2-х производителей дала следующие
результаты: за месяц после продажи в 15 из
200 материнских плат производителя А
обнаружены дефекты, тогда как среди 400
материнских плат производителя В 8%
оказались дефектами. Существенны ли
различия в надежности материнских плат
производителей А и В? Уровень значимости
принять равным 0,01.

6. Гипотезы о параметрах распределения

Пример: Гипотеза о равенстве вероятностей.
H0 : p1 = р2
H1 : p1 ≠ р2
p1 - доля бракованных деталей у производителя А
и р2 - доля бракованных деталей у производителя
В.
|Uпракт|=0,22
Uтеор=2,56
Различия в надежности материнских плат
производителей А и В несущественны.

7. Гипотезы о параметрах распределения

Данные часто можно сгруппировать по какомулибо признаку. Например, доходы студентов и
всех остальных, устойчивость ЭЦП по одному
алгоритму и по другому.
Является ли фактор, по которому проведена
группировка, важным (статистически
значимым)?
Если средние не сильно различаются, то фактор
не является значимым.
Гипотеза формулируется как гипотеза о
равенстве математических ожиданий (средних
арифметических).

8. Гипотезы о параметрах распределения

Пример:
САД, разработанные 1 и 2 фирмами работают
надежно.
Определяем среднее (время работы без сбоев) и
сравниваем (дисперсии по критерию Фишера/
по критерию Ливиня).
Ср1=53,64 Ср2=84,25 D1=303,17 D2=944,02
F=0,361<Fкрит=0,379 (уровень значимости 0,05).
Статистики не различаются.
Вычисляем t-критерий для одинаковых дисперсий.
t=-3,18<tкрит=1,7. САД двух фир работают
надежно.

9. Гипотезы о параметрах распределения

Методика:
1. Проверяем равенство дисперсий (средних).
2. Если =, то t-тест с одинаковыми дисперсиями.
Если ≠, то t-тест с разными дисперсиями.
Применение критерия Стьюдента (t-тест) зависит
от объема выборки и измеряемого признака
(тип шкалы, схема сбора данных).
Шкала: количественная
Схема: межгрупповая (или интериндивидуальная)

10. Анализ статистических связей

Гипотеза о типе зависимости признаков.
Три этапа:
Существует ли связь между
признаками?
Какова форма связи?
Какова сила (теснота) связи?

11. Анализ статистических связей

Самый простой вид связи – парная
взаимосвязь, т.е. связь между двумя
признаками.
Связь носит, как правило, причинный
характер.
Независимые переменные – факторы.
Зависимые переменные – отклики.

12. Анализ статистических связей

Виды:
Статистические.
Корреляционные.
Функциональные.

13. Статистическая связь

Зависимость между переменными, при
которой с изменением одной
переменной меняется распределение
другой.
Влияние случайных факторов велико.
Пример: Пол и категория занятости.

14. Корреляционная связь

Зависимость между переменными, при
которой с изменением одной
переменной меняется среднее
значение другой.
Пример: Количество удобрений и
урожайность, размер предприятия и
себестоимость, спрос и цена на
товары.

15. Функциональная связь

Зависимость между переменными, при
которой с изменением одной
переменной меняется значение другой
(точная зависимость).
Влияние случайных факторов =0.
Пример: Общий стаж работы y и стаж
работы x на данном предприятии
y=ax+b, b – стаж работы до
поступления на предприятие обычно
a=1, если год работы=два года стажа,
то 2 и т.д.

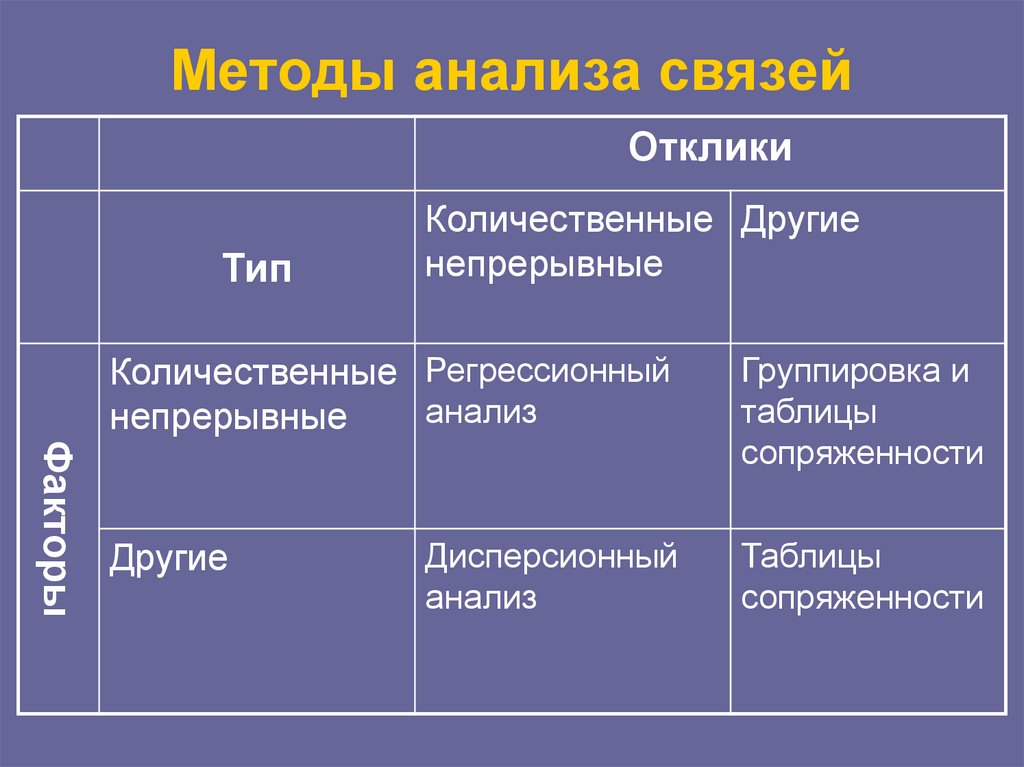
16. Методы анализа связей

Отклики
Тип
Количественные Другие
непрерывные
Факторы
Количественные Регрессионный
анализ
непрерывные
Группировка и
таблицы
сопряженности
Дисперсионный
анализ
Таблицы
сопряженности
Другие

17. Сила связи

Степень (сила) связи между двумя
переменными измеряется с помощью
специальных коэффициентов:
для двух количественных переменных:
коэффициент линейной корреляции
Пирсона;
для двух порядковых переменных (или
порядковой и количественной переменных):
коэффициент ранговой корреляции
Спирмана, мера связи тау Кендалла и тау
Стьюарта;

18. Сила связи

Степень (сила) связи между двумя
переменными измеряется с помощью
специальных коэффициентов:
для двух дихотомических переменных:
коэффициент Ф;
если хотя бы одна из переменных является
номинальной: коэффициент V Крамера,
коэффициент сопряженности C и
коэффициент Ф.

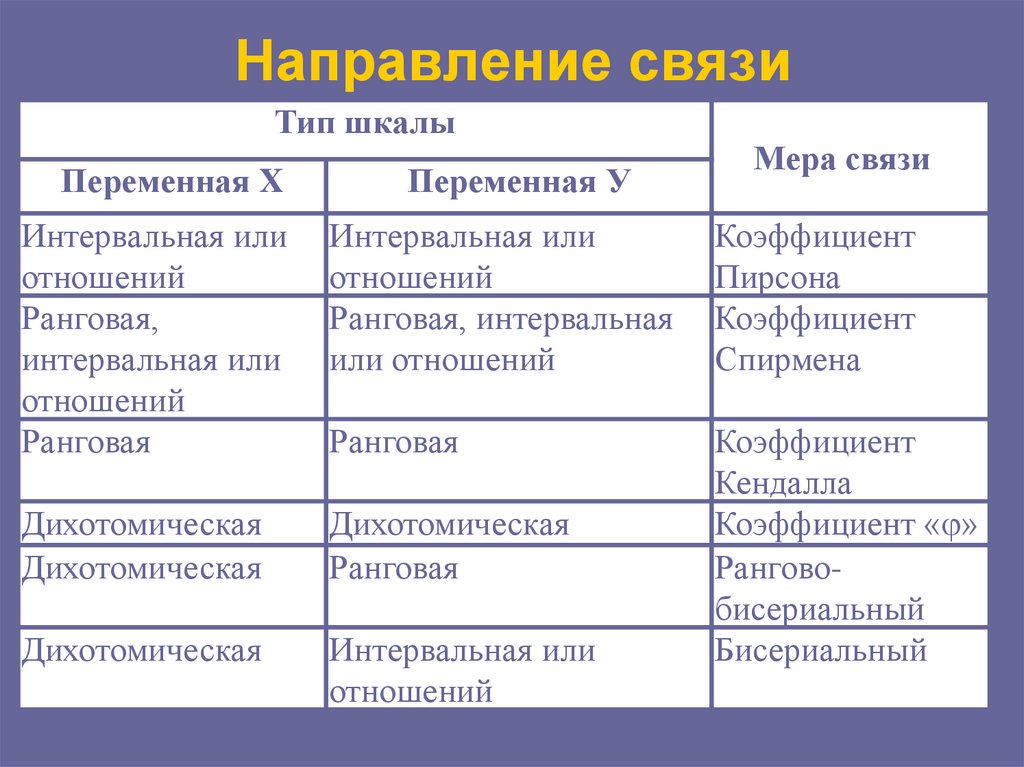
19. Направление связи

Тип шкалы
Мера связи
Переменная X
Переменная У
Интервальная или
отношений
Ранговая,
интервальная или
отношений
Ранговая
Интервальная или
отношений
Ранговая, интервальная
или отношений
Коэффициент
Пирсона
Коэффициент
Спирмена
Ранговая
Дихотомическая
Дихотомическая
Дихотомическая
Ранговая
Дихотомическая
Интервальная или
отношений
Коэффициент
Кендалла
Коэффициент « »
Ранговобисериальный
Бисериальный

20. Направление связи

• для дихотомической переменной прямая
(положительная) связь проявляется в том, что
признаки чаще появляются или не появляются
вместе, чем врозь;
• для дихотомической переменной обратная
(отрицательная) связь проявляется в том,
что признаки чаще появляются врозь, чем
вместе.
Если хотя бы одна из переменных является
номинальной, о направленности связи
говорить не приходится, и связь называется
ненаправленной.

21. Направление связи

Коэффициенты Пирсона, Спирмана и Ф, С и Ф
измеряют направленные связи, которые могут
быть прямыми или обратными:
• для порядковых и количественных
переменных связь является прямой
(положительной), если значения двух
переменных одновременно возрастают и
убывают;
• для порядковых и количественных
переменных связь является обратной
(отрицательной), если при возрастании
значений одной переменных значения второй
переменной убывают, или наоборот;

22. Свойства коэффициентов связи

при отсутствии статистической связи значение
коэффициента равно нулю;
коэффициенты ненаправленной связи
принимают значения из интервала [0,1] – чем
теснее связь, тем ближе значение
коэффициента к 1;
коэффициенты направленной связи принимают
значения из интервала [-1,+1], при этом прямой
связи соответствуют положительные значения
коэффициентов, обратной – отрицательные;
чем ближе значение коэффициента к +1 или к
–1, тем теснее связь.

23. Свойства коэффициентов связи

• сильная, или тесная при r>0,70;
• средняя при 0,50<r<0,69;
• умеренная при 0,30<r<0,49;
• слабая при 0,20<r<0,29;
• очень слабая при r<0,19.

24. Измерение силы связи

Меры связи Ф, коэффициента V Крамера,
коэффициента сопряженности C, основаны
на использовании статистики критерия 2 (хиквадрат).

25. Дисперсионный анализ

Предложен Р. Фишером.
Является статистическим методом,
предназначенным для выявления влияния ряда
отдельных факторов на результаты
экспериментов.
Относится к группе параметрических методов и
применяется только тогда, когда доказано, что
распределение является нормальным.

26. Дисперсионный анализ

Зависимая переменная (отклик, следствие) всегда
бывает количественной.
Независимые переменные (фактор, причина)
могут быть номинальными, порядковыми,
количественными (сгруппированными в
интервалы).
Проверяется гипотеза о влиянии независимых
переменных на зависимую: группы объектов,
образованные значениями факторов,
отличаются друг от друга средними значениями
зависимой переменной.

27. Дисперсионный анализ

Дисперсионный анализ позволяет исследовать
различие между группами данных, определять,
носят ли эти расхождения случайный характер
или вызваны конкретными обстоятельствами.
Например, если продажи фирмы в одном из
регионов снизились, то с помощью
дисперсионного анализа можно выяснить,
случайно ли снижение оборотов в этом регионе
по сравнению с остальными, и при
необходимости произвести организационные
изменения.

28. Дисперсионный анализ

Время решения задач – отклик.
Мотивация
Фактор:
Способ формулировки
задачи
Условия решения
задачи
Высокая
Устно
В группе
Средняя
Письменно
В одиночестве
Низкая
С применением средств
наглядности
С преподавателем
Градаций фактора должно быть не менее трех.
Недостатком дисперсионного анализа является то, что он
не дает представления о характере связи между
зависимой и независимой переменными.

29. Дисперсионный анализ

Однофакторный дисперсионный анализ (одна
независимая переменная – фактор) или
однофакторный дисперсионный анализ
Р.Фишера;
Двухфакторный дисперсионный анализ (две
независимые переменные);
Многофакторный дисперсионный анализ.
Влияние факторов определяется по F-критерию
Фишера.

30. Однофакторный дисперсионный анализ

Гипотеза:
Пусть фактор имеет k значений (образует k
групп).
H 0 : 1 2 ... k (во всех группах средние
значения зависимой переменной равны);
H1 : i
(хотя бы для некоторых групп
средние значения не равны).
Если полученное значения критерия Фишера
больше табличного (критического), то нулевая
гипотеза отклоняется.

31. Однофакторный дисперсионный анализ

Пример 1:
Три группы студентов изучали информатику по
разным методикам. В конце года провели
тестовый контроль знаний у случайно
отобранных студентов из каждой группы
(соответственно 7, 5 и 3 человек). Обучаемые
допустили следующее число ошибок:
1 группа: 1, 3, 2, 1, 0, 2, 1
2 группа: 2, 3, 4, 1, 4
3 группа: 4, 5, 3
При уровне значимости 0,05 требуется проверить
гипотезу об отсутствии влияния методики на
результат (о равенстве математических
ожиданий числа ошибок в группах).

32.

Ho: m1= m2 =m3
Н1: m1≠ m2 ≠ m3
Однофакторный дисперсионный анализ для
несвязанных выборок: в данном примере
влиянию каждой из градаций подвергаются
разные выборки испытуемых.
Fфакт=6,52 > F крит=3,89
Статистика попала правее квантили, т.е. в
критическую область, следовательно нулевая
гипотеза Ho отклоняется и принимается
альтернативная Н1 : методика обучения
значимо влияет на результат.

33. Однофакторный дисперсионный анализ

Пример 2: Группа из 5 испытуемых была
обследована с помощью трех
экспериментальных заданий, направленных на
изучение интеллектуальной настойчивости.
Испытуемым индивидуально предъявлялись
последовательно три одинаковые анаграммы:
четырехбуквенная, пятибуквенная и
шестибуквенная.
При уровне значимости 0,05 требуется проверить
гипотезу о влиянии длины анаграммы на
длительность попыток ее решения.

34.

Наборов гипотез в данном случае два.
Набор А.
Н0(А): Различия в длительности попыток решения
анаграмм разной длины являются не более
выраженными, чем различия, обусловленные
случайными причинами.
Н1(А): Различия в длительности попыток решения
анаграмм разной длины являются более
выраженными, чем различия, обусловленные
случайными причинами.

35.

Набор В.
Но(В): Индивидуальные различия между
испытуемыми являются не более выраженными,
чем различия, обусловленные случайными
причинами.
Н1(В): Индивидуальные различия между
испытуемыми являются более выраженными, чем
различия, обусловленные случайными причинами.

36.

Условие 1.
Код
Четырехбуквенн
испытуемого
ая анаграмма
1
5
Условие 2.
Пятибуквенная
анаграмма
235
Условие 3.
Шестибуквенная
анаграмма
7
Суммы по
испытуемым
247
2
7
604
20
631
3
2
93
5
100
4
2
171
8
181
5
35
141
7
183
суммы
51
1244
47
1342
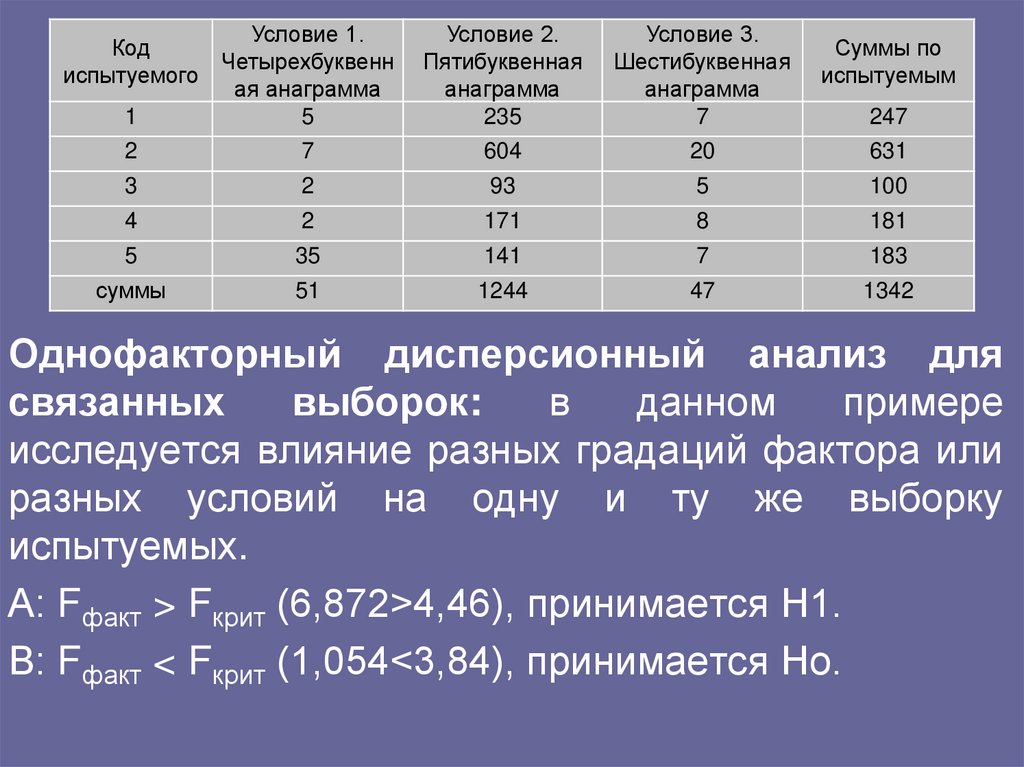
Однофакторный дисперсионный анализ для
связанных
выборок:
в
данном
примере
исследуется влияние разных градаций фактора или
разных условий на одну и ту же выборку
испытуемых.
А: Fфакт > Fкрит (6,872>4,46), принимается Н1.
В: Fфакт < Fкрит (1,054<3,84), принимается Но.

37. Двухфакторный дисперсионный анализ

В двухфакторном анализе
рассматриваются три вида группировок
зависимой переменной:
по первому фактору (который принято
называть фактором А),
по второму фактору (фактор В),
перекрестная группировка по двум
факторам.

38. Двухфакторный дисперсионный анализ

Для двухфакторного дисперсионного анализа
проверяются гипотезы трех видов (каждая
отдельно):
1. Гипотеза о влиянии на зависимую
переменную фактора А (об эффекте
фактора А):
H 0 : 1. 2. ... k . (во всех k группах,
образованных фактором А, средние
значения зависимой переменной равны)
H 1 : i. (хотя бы для некоторых групп
средние значения не равны).

39. Двухфакторный дисперсионный анализ

2. Гипотеза о влиянии на зависимую переменную
фактора В (об эффекте фактора В):
H 0 : .1 .2 ... .l (во всех l группах, образованных
фактором В, средние значения зависимой переменной
равны)
H 1 : i. (хотя бы для некоторых групп средние
значения не равны).
3. Гипотеза о влиянии на зависимую переменную
взаимодействия факторов А и В (об эффекте
взаимодействия):
H 0 : .1 ij i. . j 0 для любых
i 1, k j 1, l ; (эффект
взаимодействия отсутствует)
H 1 : .1 ij i. . j 0 хотя бы для некоторых
i иj
(эффект взаимодействия имеет место).

40. Двухфакторный дисперсионный анализ

ПРИМЕР:
Гипотеза: на продолжительность рабочей недели
(зависимая переменная) влияют образование
(фактор А), пол (фактор В), а также их
взаимодействие. В данном случае о наличии
эффекта взаимодействия свидетельствовали
бы противоположные тенденции зависимости
продолжительности рабочей недели у мужчин
и женщин: например, у мужчин с повышением
уровня образования она бы увеличивалась, а у
женщин – уменьшалась.

41. Т-критерий

Позволяет ответить на вопрос:
насколько существенны
различия между двумя
выборками по данной
количественной переменой.
Основание применения:
межгрупповая схема сбора
информации. Распределение –
нормальное.
Как правило группирующая
переменная дискретна и имеет
две градации.

42. Т-критерий

Например, надо выяснить, влияет ли способ
упаковки кофе на его потребительские качества
через год после хранения. Или: отличается ли
потребительское поведение мужчин и женщин.
Если отличается – рекламные ролики и плакаты
надо делать отдельно для мужчин и отдельно
для женщин. Если нет – рекламная кампания
может быть единой.
Требуется проверить их однородность.

43. Т-критерий

Противоположным понятием является
«различие».
Например, необходимо выделить сегменты
потребительского рынка. Если установлена
однородность двух выборок, то возможно
объединение сегментов. Это позволит
осуществлять по отношению к ним одинаковую
маркетинговую политику. Если же установлено
различие (поведение потребителей в двух
сегментах различно) объединять сегменты
нельзя, маркетинговые политики будут
различны.

44. Т-критерий

1. t-критерий для независимых выборок.
2. t-критерий для парных выборок.
3. одновыборочный t-критерий.

45. Т-критерий

Пример 1: Сравнить между собой
результаты выполнения тестов на внимание
в двух группах.
Пример 2: Отличается ли средний возраст
жителей Северо-Кавказского Федерального
округа от общего по России.
Пример 3: Сравнить между собой результаты
выполнения логических задач до и после
курса обучения.

46. Таблицы сопряженности

Средство представления совместного
распределения двух переменных,
предназначенное для исследования
связи между ними.
Является наиболее универсальным
средством изучения статистических
связей, так как в ней могут быть
представлены переменные с любым
уровнем измерения.

47. Таблицы сопряженности

Двумерное частотное распределение,
показывает какие пары значений
встречаются в выборке и сколько раз
встречается каждая пара.
В таблице сопряженности могут быть
представлены как абсолютные, так и
относительные частоты (по
отдельности или одновременно).

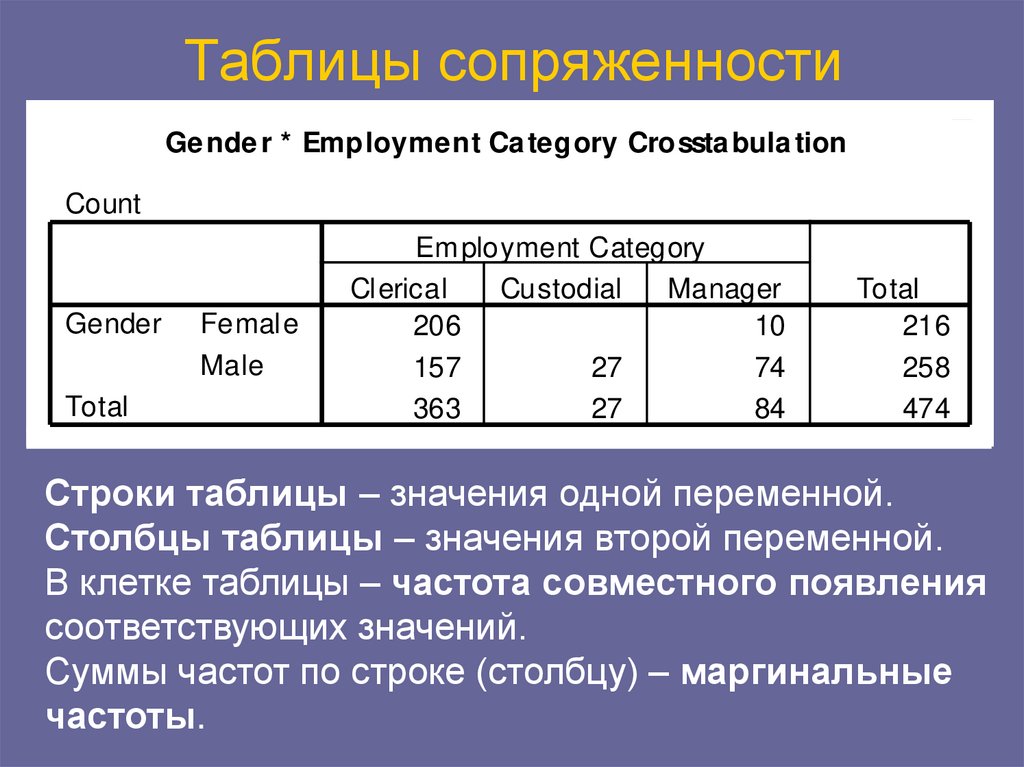
48. Таблицы сопряженности

Ge nde r * Employment Ca tegory Crossta bula tion
Count
Gender
Total
Female
Male
Employment Category
Clerical
Custodial
Manager
206
10
157
27
74
363
27
84
Total
216
258
474
Строки таблицы – значения одной переменной.
Столбцы таблицы – значения второй переменной.
В клетке таблицы – частота совместного появления
соответствующих значений.
Суммы частот по строке (столбцу) – маргинальные
частоты.

49. Таблицы сопряженности

Таблица сопряженности может быть построена
для дискретных переменных (номинальных,
порядковых, количественных), а также для
непрерывных переменных, сгруппированных
в интервалы.
Следует избегать ситуаций, когда частоты в
клетках таблицы слишком малы (за
исключением тех случаев, когда отдельные
категории объектов отсутствуют в принципе –
например, женщины-охранники). Для
повышения частот в клетках значения
переменных рекомендуется группировать.

50. Таблицы сопряженности

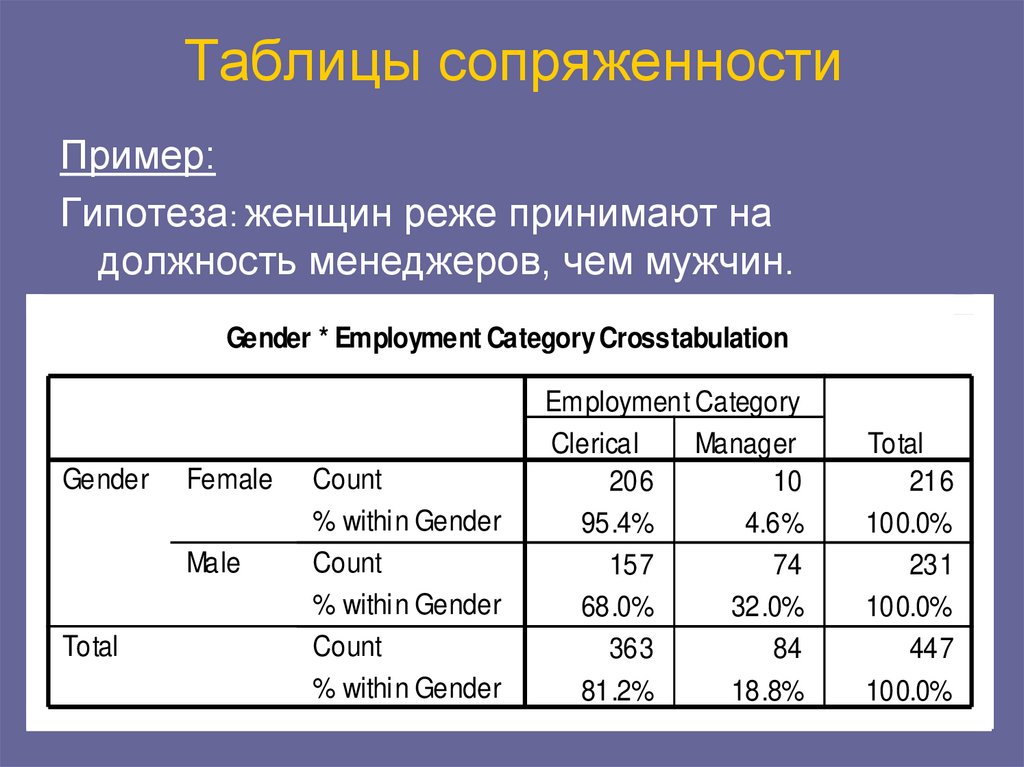
Пример:
Гипотеза: женщин реже принимают на
должность менеджеров, чем мужчин.
Gender * Employment Category Crosstabulation
Gender
Female
Male
Total
Count
% within Gender
Count
% within Gender
Count
% within Gender
Employment Category
Clerical
Manager
206
10
95.4%
4.6%
157
74
68.0%
32.0%
363
84
81.2%
18.8%
Total
216
100.0%
231
100.0%
447
100.0%

51. Регрессионный анализ

Служит для определения вида связи и дает
возможность для прогнозирования
значения одной (зависимой) переменной
отталкиваясь от значения другой
(независимой) переменной.
Обычно предполагается, что случайная
величина имеет нормальный закон
распределения.
Фактор, отклик: количественные.

52. Регрессионный анализ

Моделирование:
• дорожных аварий как функции скорости,
дорожных условий, погоды и т.д., чтобы
проинформировать милицию и снизить
несчастные случаи;
• объема документооборота как функции
направлений деятельности, внешних условий
функционирования организации с целью
оптимизации.

53. Регрессионный анализ

Прогнозирование:
• объема потребляемой электроэнергии в
следующем году по прогнозам населения и
типичным погодным условиям;
• результатов работы подразделений
предприятия, основываясь на выборке
показателей удовлетворенности методами
мотивации.

54. Регрессионный анализ

Простая линейная регрессия.
Множественная линейная регрессия.
Нелинейная регрессия.
Бинарная логистическая регрессия.
Мультиноминальная логистическая регрессия.
Порядковая регрессия.

55. Простая линейная регрессия

.
y bx b0
Если между двумя переменными существует
линейная связь, то при увеличении значения
переменной х значение переменной у
пропорционально увеличивается (прямая,
положительная связь) или уменьшается
(обратная, отрицательная связь).

56. Линейная регрессия

Уравнение y bx b0 – статистическая модель
причинной линейной связи, уравнение
регрессии.
х – независимая переменная;
у – зависимая;
b – коэффициент регрессии. Показывает, насколько, в
среднем, увеличится или уменьшится значение
зависимой переменной y при увеличении значения
независимой переменной x на 1:
увеличение числа рабочих на 1 чел. приводит в
среднем к увеличению объема годового
производства на 2984 руб.

57. Простая линейная регрессия

140000
120000
100000
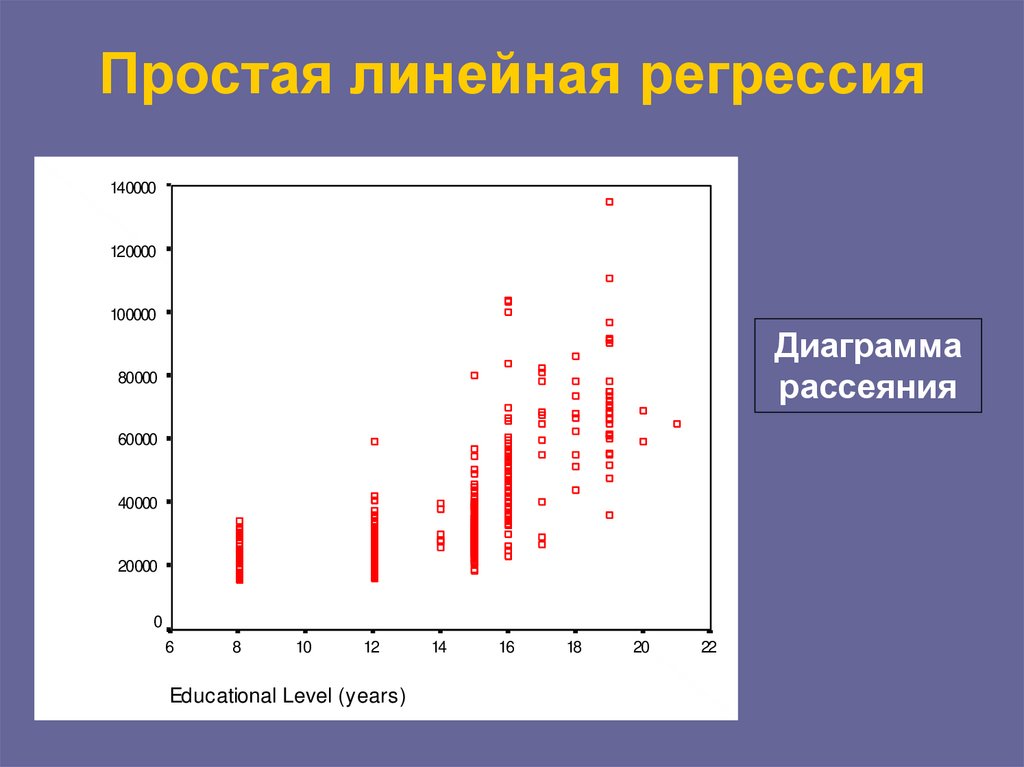
Диаграмма
рассеяния
80000
60000
40000
20000
0
6
8
10
12
Educational Level (years)
14
16
18
20
22

58.

Простая линейная регрессия
Линейная связь является:
полной, если все точки на диаграмме
рассеяния лежат на прямой y bx b0 ;
сильной или тесной, если облако точек
прилегает к прямой достаточно близко;
слабой, если облако точек по отношению к
прямой широко разбросано.

59. Линейная регрессия

Теснота (сила) линейной связи измеряется с
помощью коэффициента линейной
корреляции Пирсона.
n
r
x x y y
i
i 1
n
i
n
x x y y
i 1
2
i
i 1
i
2

60. Линейная регрессия

Коэффициент Пирсона обладает следующими
свойствами:
• 1 r 1 ;
• r=0, если между переменными нет связи, или
если связь не является линейной;
• r>0, если линейная связь является прямой
(положительной);
• r<0, если линейная связь является обратной
(отрицательной). Чем ближе значение к +1 или
к –1, тем теснее связь;
• r=+1, если связь является полной.

61. Линейная регрессия

Эстонский исследователь Я. Микк, изучая трудности понимания
текста, установил «формулу читаемости», которая
представляет собой множественную линейную регрессию:
y=0.01x1+0.27x2+0.54x3-2.51 — оценка трудности понимания
текста,
где х1 - длина самостоятельных предложений в количестве
печатных знаков,
х2 - процент различных незнакомых слов,
х3 - абстрактность повторяющихся понятий, выраженных
существительными.
Сравнивая между собой коэффициенты регрессии, выражающие
степень влияния факторов, можно видеть, что трудность
понимания текста определяется прежде всего его
абстрактностью. Вдвое меньше (0,27) трудность понимания
текста зависит от числа незнакомых слов и практически она
совсем не зависит от длины предложении.