Дисперсионный анализ

1.

{ Дисперсионный анализ

2. Постановка проблемы

Дисперсионный
анализ
является
статистическим методом анализа результатов
наблюдений,
зависящих
от
различных
одновременно действующих факторов, с целью
выбора наиболее значимых факторов и оценки
их влияния на исследуемый процесс.
Методами
дисперсионного
анализа
устанавливается наличие влияния заданного
фактора на изучаемый процесс (на выходную
переменную процесса) за счёт статистической
обработки
наблюдаемой
совокупности
выборочных данных.

3.

Основной целью дисперсионного анализа
является исследование значимости различия
между средними.
Установить различаются ли три группы или
более по какому-либо одному
количественному признаку
Например определить, зависит ли активность фермента
от стадии заболевания

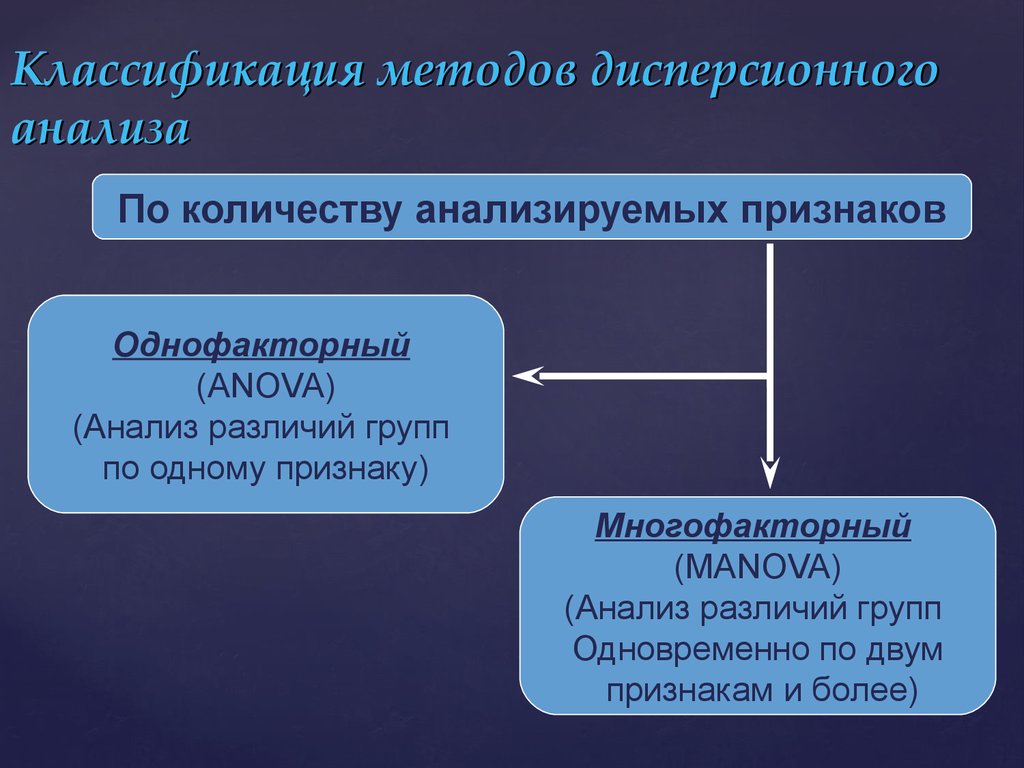
4. Классификация методов дисперсионного анализа

По количеству анализируемых признаков
Однофакторный
(ANOVA)
(Анализ различий групп
по одному признаку)
Многофакторный
(МANOVA)
(Анализ различий групп
Одновременно по двум
признакам и более)

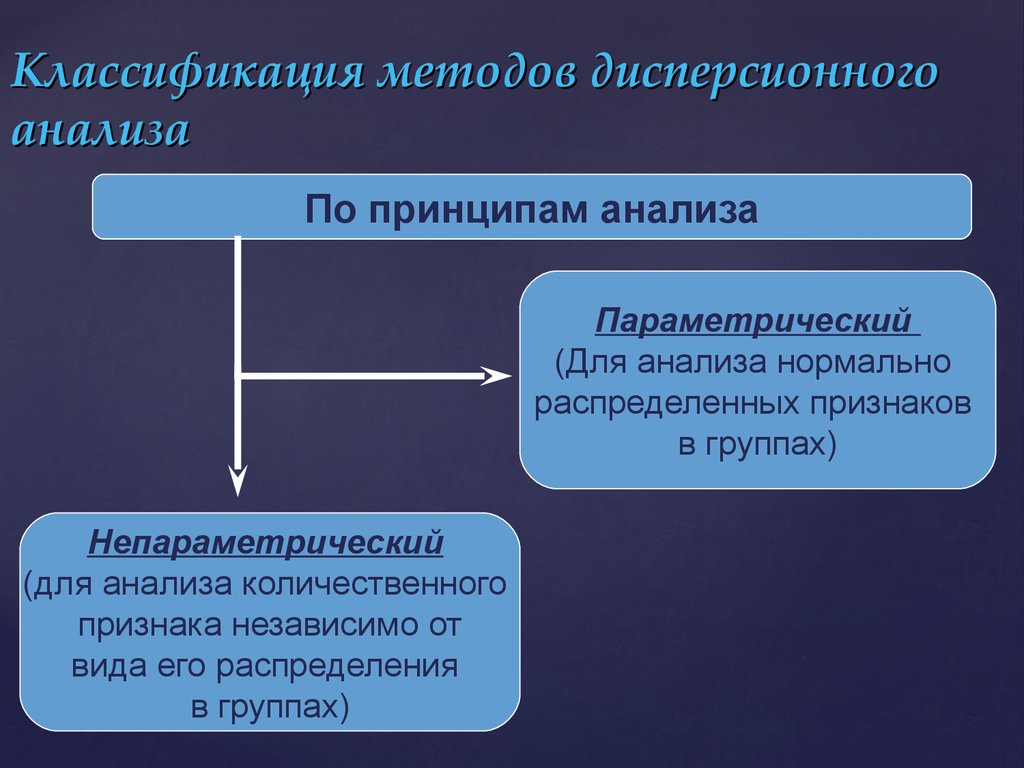
5. Классификация методов дисперсионного анализа

По принципам анализа
Параметрический
(Для анализа нормально
распределенных признаков
в группах)
Непараметрический
(для анализа количественного
признака независимо от
вида его распределения
в группах)

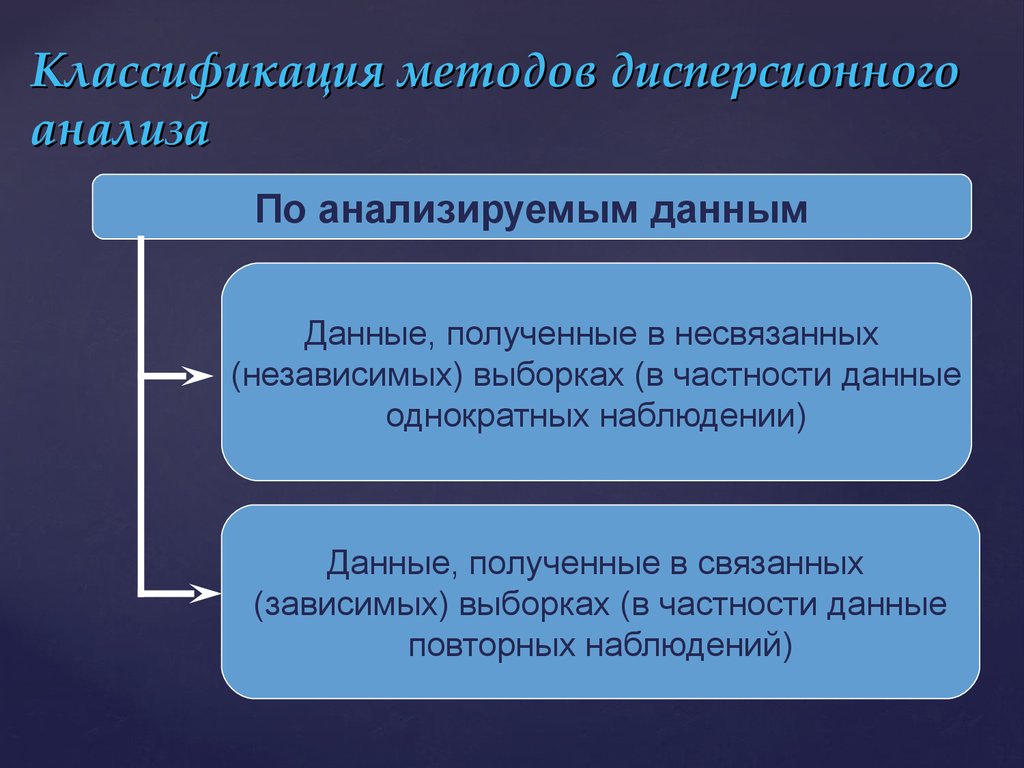
6. Классификация методов дисперсионного анализа

По анализируемым данным
Данные, полученные в несвязанных
(независимых) выборках (в частности данные
однократных наблюдении)
Данные, полученные в связанных
(зависимых) выборках (в частности данные
повторных наблюдений)

7. Параметрический дисперсионный анализ

Сравнить три или более группы по
количественному нормально
распределенному признаку
В процедуре параметрического анализа
вариаций общая вариация данных
рассматривается как сумма двух видов
вариаций:
Параметрический дисперсионный
анализ

8. Параметрический дисперсионный анализ

1. Межгрупповая вариация – вариация между
средним каждой группы и общим средним
значением всей выборки
2. Внутригрупповая вариация – вариация
между каждым объектом исследования
группы и средним значением
соответствующей группы
Параметрический дисперсионный
анализ

9. Параметрический дисперсионный анализ

Этапы выполнения:
Проверка гипотез о равенстве
дисперсий
Собственно анализ вариаций
Апостериорное сравнение групп
с помощью специализированных
процедур, отличных от Ткритерия
Параметрический дисперсионный
анализ

10. Проверка гипотез о равенстве дисперсий ( тест Левена )

Происходит проверка нулевой гипотезы
об отсутствии различий дисперсий в группах
Если результат свидетельствует об
отсутствии различия дисперсий
( р>0,05), то применение
параметрического дисперсионного
анализа обосновано
Если различие дисперсий имеется
( р<0,05), то применять
параметрический дисперсионный
анализ не следует
Проверка гипотез о равенстве
дисперсий ( тест Левена )

11. Непараметрические методы исследования независимых групп (м-д Краскела-Уоллиса, медианный тест)

Используется в случае необходимости сопоставить несколько
групп по одному количественному или порядковому
признаку независимо от вида его распределения в группах

12.

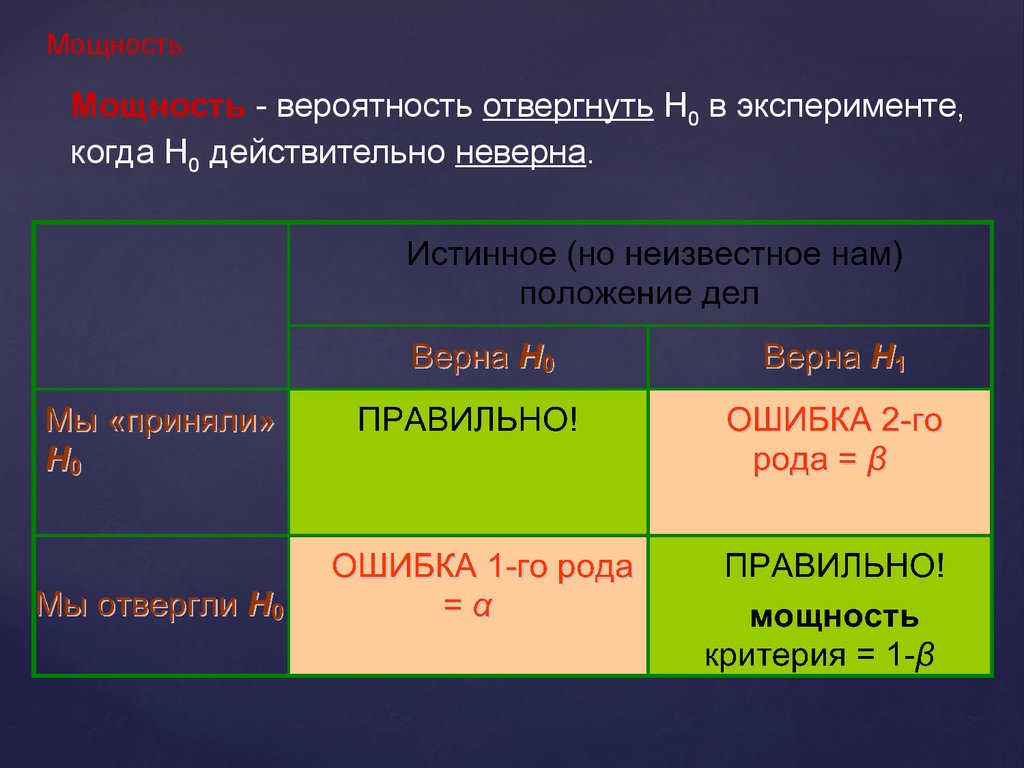
Мощность
Мощность - вероятность отвергнуть Н0 в эксперименте,
когда Н0 действительно неверна.

13.

Мощность
Мощность предполагаемого статистического теста ключевой элемент планирования исследования
«Реальное значение» параметра:
Во всей мировой популяции землероек μ = 90 г.
Пусть «реальное значение» средней массы в
заповеднике = 94 г.

14.

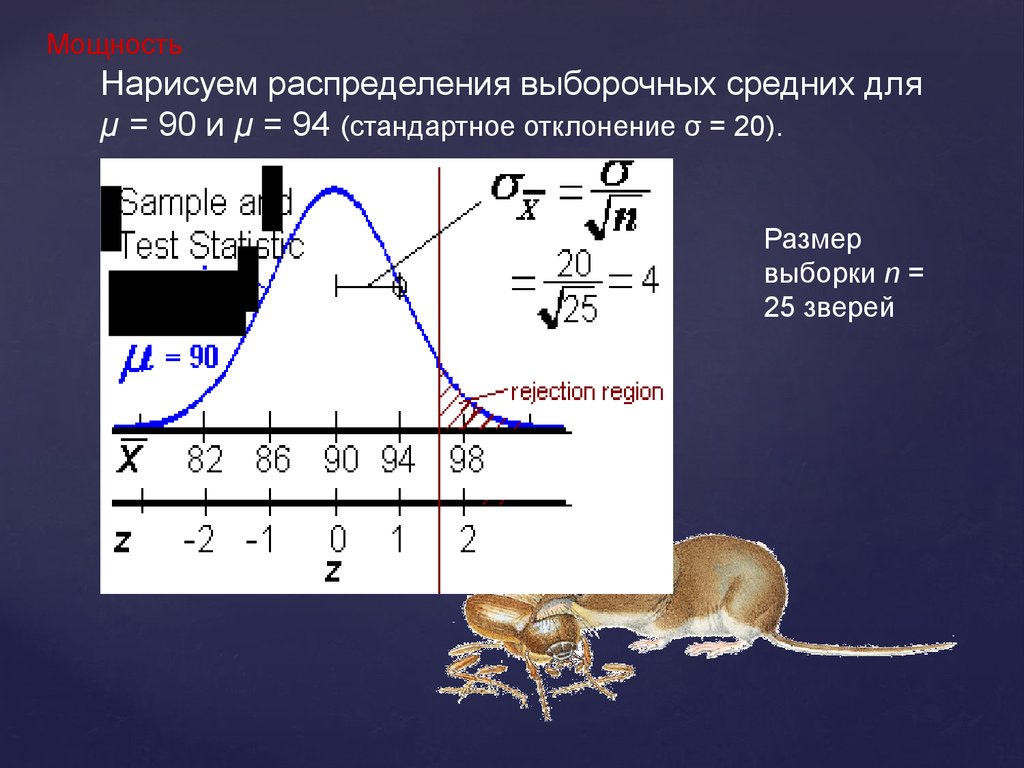
Мощность
Нарисуем распределения выборочных средних для
μ = 90 и μ = 94 (стандартное отклонение σ = 20).
Размер
выборки n =
25 зверей

15.

Мощность
Как увеличить мощность?
Большей МОЩНОСТИ критерия способствуют:
1.
2.
3.
4.
5.
Большой размер выборки;
Большие различия между популяциями (effect size);
Маленькое стандартное отклонение;
Большой уровень значимости (α=0.05 а не α=0.01);
Выбор одностороннего теста вместо двустороннего

16. Базовая модель

Математическая основа базовой модели:
SSобщ = SSA + SSB + SSост
Где SS – это сумма квадратов отклонений от
среднего.
{
Рассмотрим случай, когда комбинация
определенных значений A и B встречается
у равного количества человек r, число
возможных значений B равно b и число
возможных значений A равно a.
(сбалансированная модель).

17.

{

18. Базовая модель

S
b
r
(
x
)
a
S (x )
a
2
A
i
i
1
b
2
B
j
j
1
a
b
r
2
ост
i
j
k
i
j
i
1jk
1
Базовая модель
Тогда общее число человек в выборке
n=axbxr
{

19. Базовая модель

В основе лежит все та же основная
модель дисперсионного анализа, что
и в случае однофакторной статистики,
только теперь мы изучаем действие
двух или более факторов:
{
x=m+α+β+…+ε

20. Базовая модель

Источник
вариации
SS
Общий
Фактор А
Фактор B
{
Главные
эффекты
Случайные
отклонения
df
MS
F
SSобщ
abr-1
MSобщ
SSA
a-1
MSA
MSA / MSост
SSB
b-1
MSB
MSB / MSост
SSмод = SSA a + b -2 MSмод
+ SSB
SSост
ab(r-1)
MSост
MSмод / MSост

21. Модель с эффектом взаимодействия

S
(x x )
a
b
2
A
Bi
i1jji j
Модель с эффектом взаимодействия
Эффект взаимодействия
предусматривает то, что дисперсия
общего влияния факторов не равна
простой сумме их дисперсий:
{
SSобщ = SSA + SSB + SSAB + SSост
Вводится еще один компонент –
взаимодействие A и B.

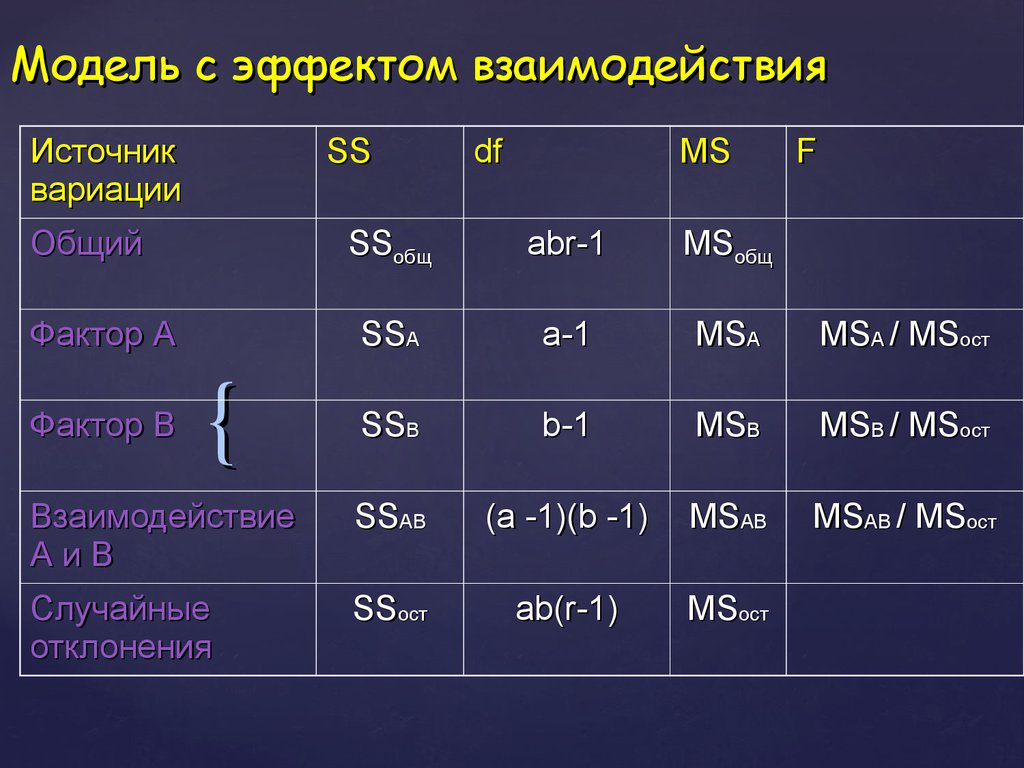
22. Модель с эффектом взаимодействия

Источник
вариации
SS
Общий
df
MS
F
SSобщ
abr-1
MSобщ
SSA
a-1
MSA
MSA / MSост
SSB
b-1
MSB
MSB / MSост
Взаимодействие
AиB
SSAB
(a -1)(b -1)
MSAB
MSAB / MSост
Случайные
отклонения
SSост
ab(r-1)
MSост
Фактор А
Фактор B
{

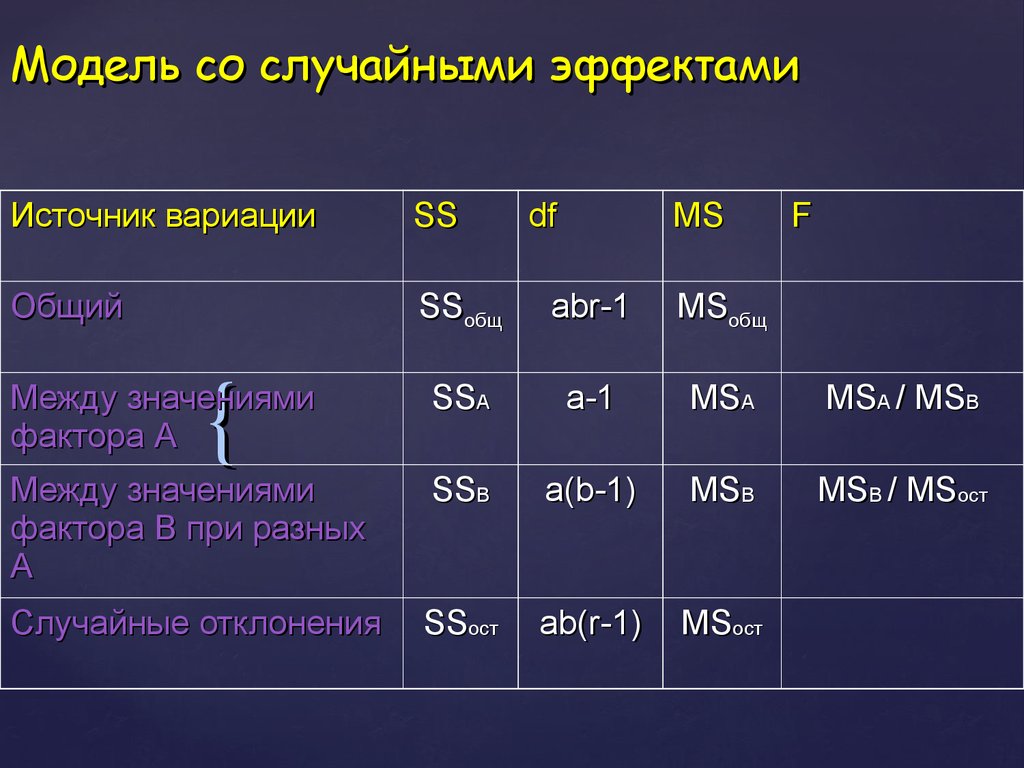
23. Модель со случайными эффектами

Случайные факторы предусматривают
другой подход к вычислению
компонентов дисперсии. Если все
факторы случайны, то в модели
{
x=m+a+b+e
при справедливости нулевой гипотезы
a, b и e распределены нормально со
средним = 0 и разными дисперсиями.

24. Модель со случайными эффектами

Источник вариации
SS
Общий
SSобщ
abr-1
MSобщ
Между значениями
фактора А
SSA
a-1
MSA
MSA / MSB
Между значениями
фактора B при разных
A
SSB
a(b-1)
MSB
MSB / MSост
Случайные отклонения
SSост
ab(r-1)
MSост
{
df
MS
F

25. Модель со случайными эффектами

S
r
(x )
a
b
2
A
Bi
i1jji
Модель со случайными эффектами
Поскольку подход к SSB иной,
рассчитывается он тоже по-другому:
{
Если в модели со случайными
эффектами есть взаимодействия, их
дисперсия считается так же, как и в
модели постоянных эффектов.

26. Модель с несколькими эффектами

Чем больше факторов в модели, тем
сложнее ее расчет и построение.
Так, например, если в модели три фактора,
то оценка влияния одного фактора на
модель в целом можно провести только
после исключения его взаимодействия с
другими факторами:
{
MSABC / MSост – взаимодействие всех факторов
MSAB / MSABC - взаимодействие двух факторов
MSAС / MSABC - взаимодействие двух факторов

27. Немного терминологии

Уровень (level) – это одно из возможных
значений фактора. В англоязычной
литературе фактор принято
обозначать в виде его номера и
количества уровней: 2x2, 3x4 и т.п.
{
Ячейка/гнездо (cell) – это группа
значений при заданной комбинации
факторов (например, ячейка A=1, B=2,
C=10)

28. Немного терминологии

Полный перекрестный дизайн (Completely
crossed design) – каждый уровень каждого
фактора встречается в комбинации со
всеми уровнями остальных факторов.
{
Сбалансированный дизайн (balanced design) в каждой ячейке равное количество
значений.
Ортогональный дизайн (orthogonal design) –
сбалансированный, полный перекрестный
дизайн при условии случайной выборки.

29. Простой пример

Изучаются 2 фактора, влияющих на сдачу экзамена:
• Употребление кофе (да/нет)
• Наличие конспекта (да/нет)
Результат оценивается в количестве правильных ответов на
вопросы единого междисциплинарного теста.
{
Конспект (Фактор A)
Кофеин (Фактор
B)
Нет
Да
Да
Только кофеин
Оба
Нет
Контроль (ни
одного)
Только конспект

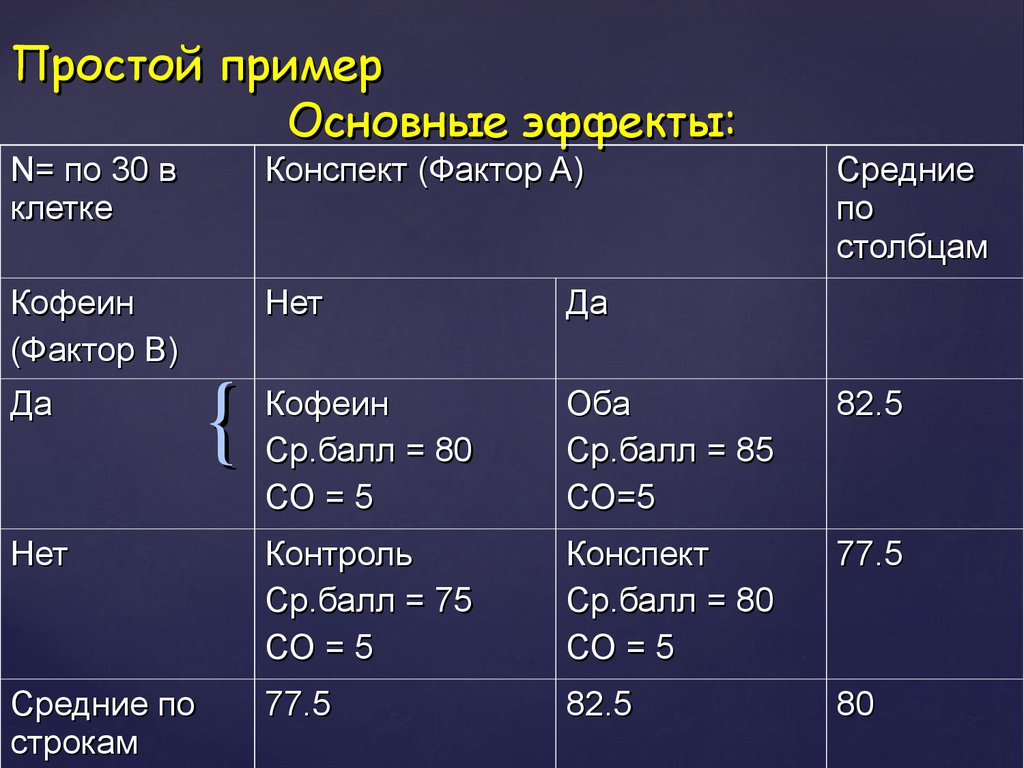
30. Простой пример

Основные эффекты:
N= по 30 в
клетке
Конспект (Фактор A)
Кофеин
(Фактор B)
Нет
Да
Кофеин
Ср.балл = 80
СО = 5
Оба
Ср.балл = 85
СО=5
82.5
Нет
Контроль
Ср.балл = 75
СО = 5
Конспект
Ср.балл = 80
СО = 5
77.5
Средние по
строкам
77.5
82.5
80
Да
{
Средние
по
столбцам

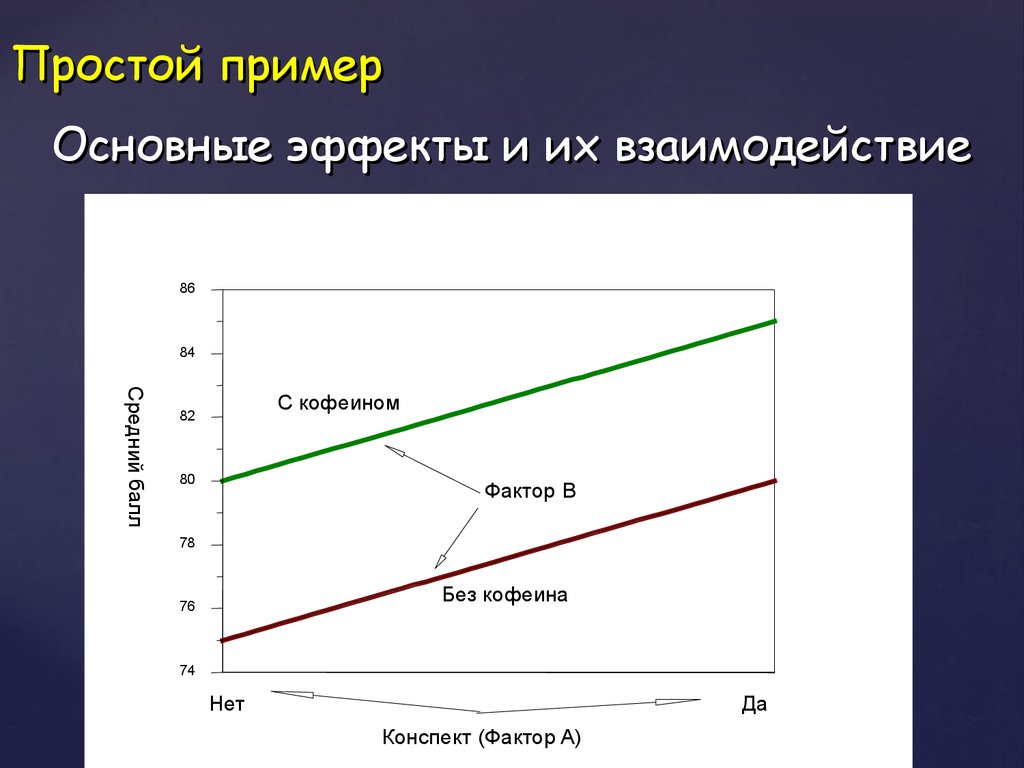
31. Простой пример

Основные эффекты и их взаимодействие
86
84
Средний балл
82
80
{
С кофеином
Фактор B
78
Без кофеина
76
74
Нет
Да
Конспект (Фактор A)

32. Простой пример

Основные эффекты и их взаимодействие
Эффекты факторов видны по наклону линий
на графике (первый эффект) и точках
пересечения линий с вертикальной осью
(второй эффект)
{
Взаимодействие факторов проявляется в
виде нарушения параллельности линий на
графике.

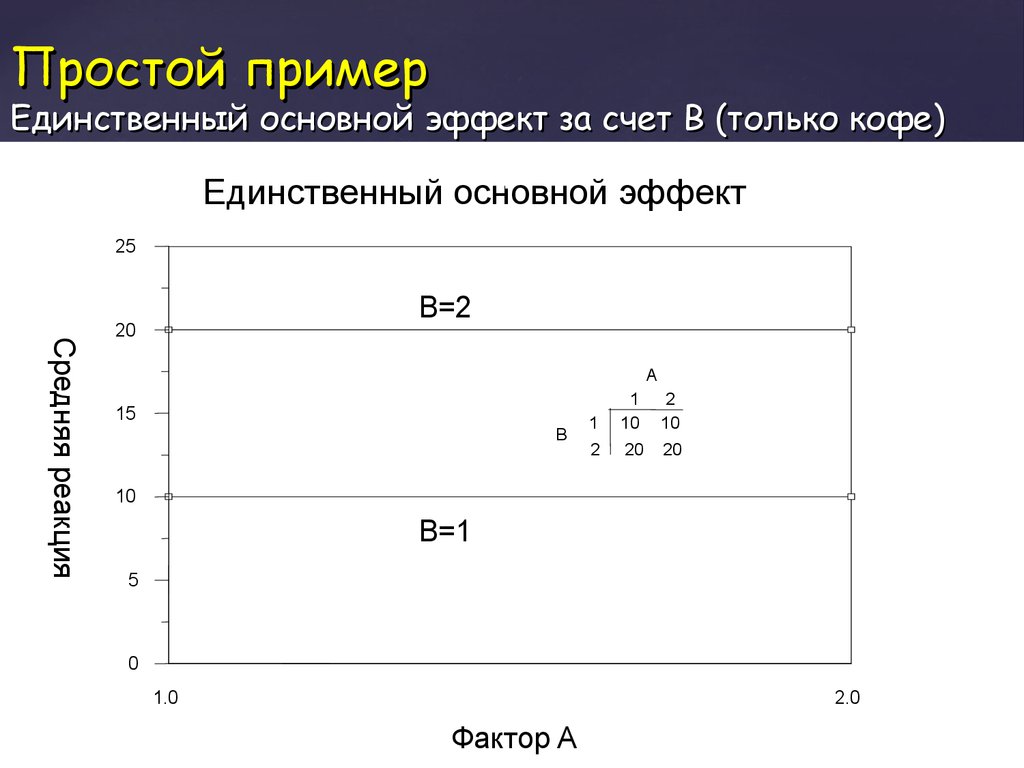
33. Простой пример Единственный основной эффект за счет B (только кофе)

Единственный основной эффект
25
B=2
Средняя реакция
20
{
15
A
B
1
1
10
2
10
2
20
20
10
B=1
5
0
1.0
2.0
Фактор A

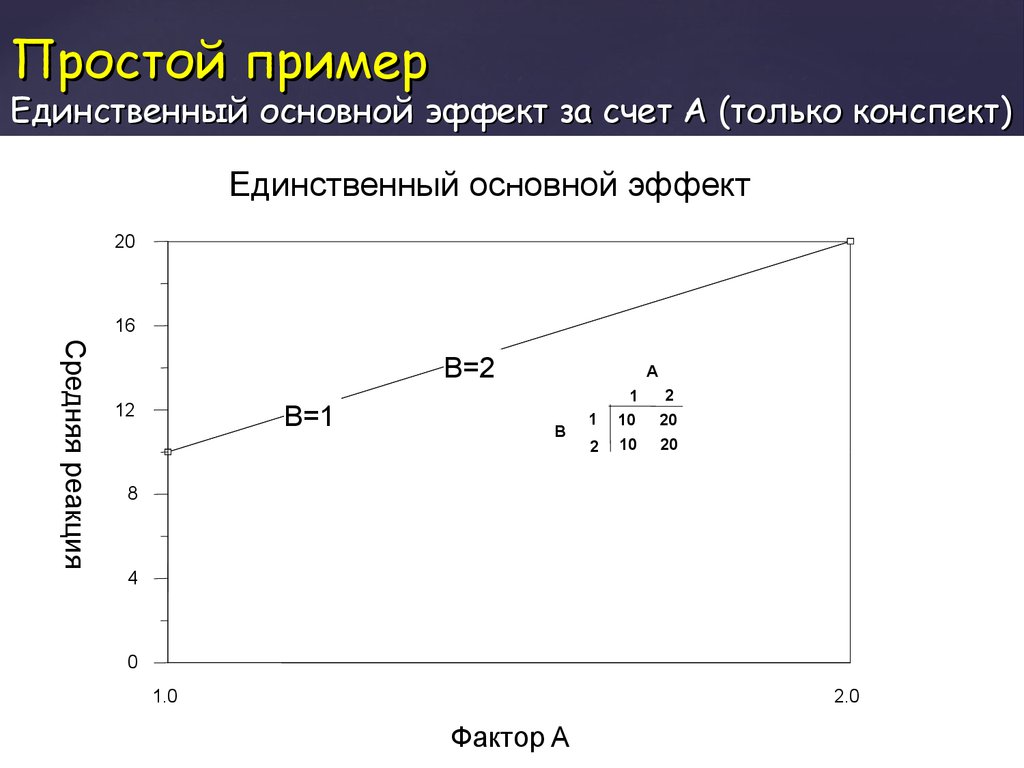
34. Простой пример Единственный основной эффект за счет А (только конспект)

Единственный основной эффект
20
16
Средняя реакция
{
12
B=2
B=1
A
B
1
2
1
10
20
2
10
20
8
4
0
1.0
2.0
Фактор A

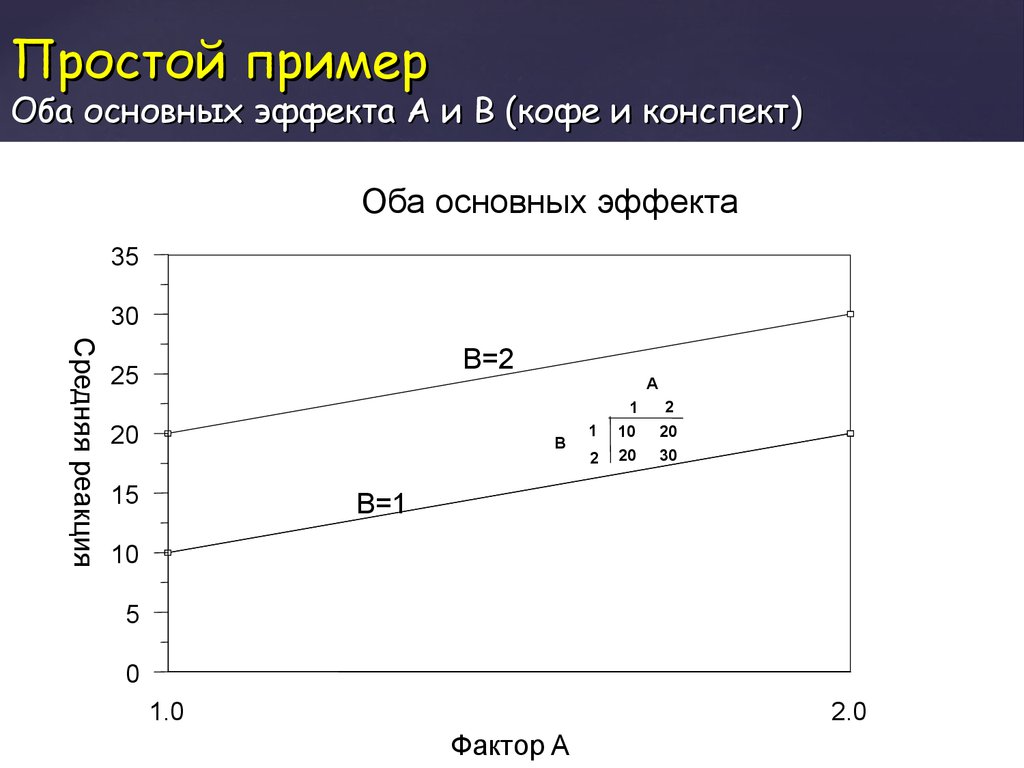
35. Простой пример Оба основных эффекта A и B (кофе и конспект)

Оба основных эффекта
35
30
Средняя реакция
B=2
{
25
20
15
A
B
1
2
1
10
20
2
20
30
B=1
10
5
0
1.0
2.0
Фактор A

36. Однофакторный дисперсионный анализ

Рассмотрим оценки различных дисперсий, возникающие при анализе
таблицы результатов наблюдений. Для оценки дисперсии,
характеризующей изменение данных на уровне Ai (по строкам
таблицы), имеем:
2
n
n
1
1
2
2
2 1
xij xij .
Si
( xij xi )
n 1 j 1
n 1 j 1
n j 1
n
Из предпосылок дисперсионного анализа следует, что должно иметь
место равенство всех дисперсий. При выполнении этого условия
находим оценку дисперсии, характеризующей рассеяние значений xij
вне влияния фактора A, по формуле:
2
k n
k n
1
1
1
1
2
2
2
2
xij xij
S 0 Si
( xij xi )
k i 1
k (n 1) i 1 j 1
k (n 1) i 1 j 1
n i 1 j 1
k
k
n

37. Однофакторный дисперсионный анализ

Для упрощения вычислений приведем алгоритм их выполнения.
Вычисляем последовательно суммы:
k
n
Q1
i 1 j 1
2
S0
1
2
Q2 X i
n i 1
k
2
xij
Q1 Q2
k (n 1)
2
СравниваемS A
фактора A.
2
SA
2
S0 и
1
Q3 X i
kn i 1
k
2
Q2 Q3
k 1
устанавливаем наличие влияния
k (n 1) Q2 Q3
F [k 1; k (n 1)]
Если
k 1 Q1 Q2
значимо.
, то влияние A –

38. Двухфакторный дисперсионный анализ

Рассмотренный ранее однофакторный дисперсионный анализ обладает информативностью, не
большей, чем методы множественного сравнения
средних.
Информативность
дисперсионного
анализа возрастает при одновременном изучении
влияния нескольких факторов.
Рассмотрим случай, когда анализируется влияние
одновременно двух факторов A и B.

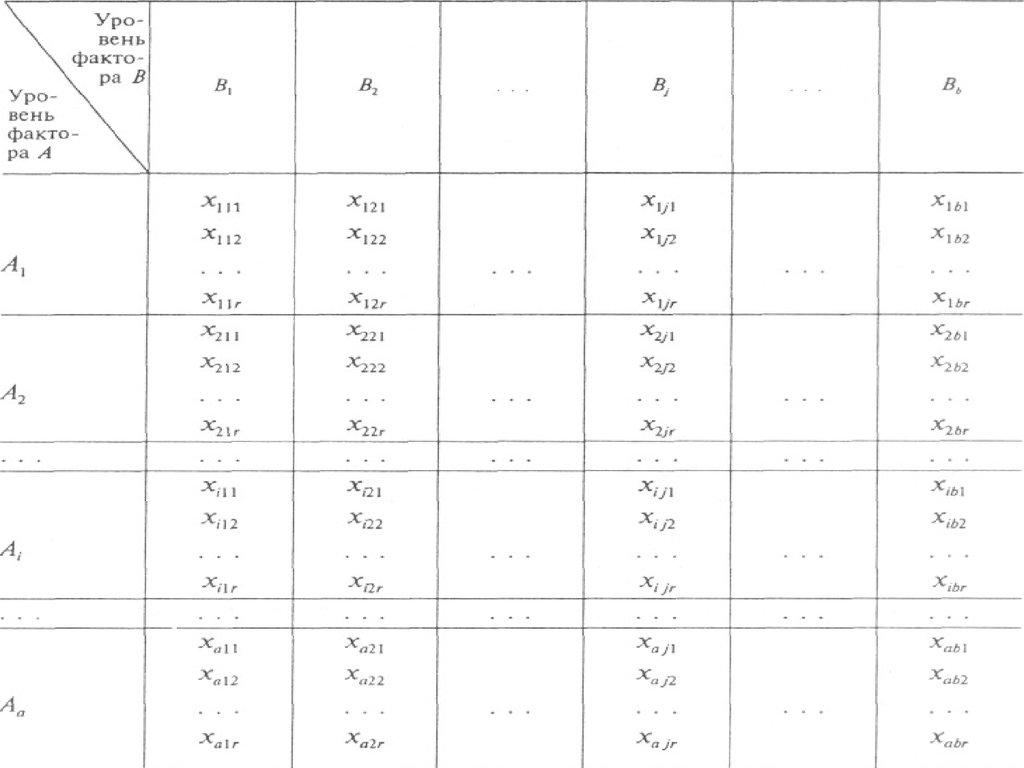
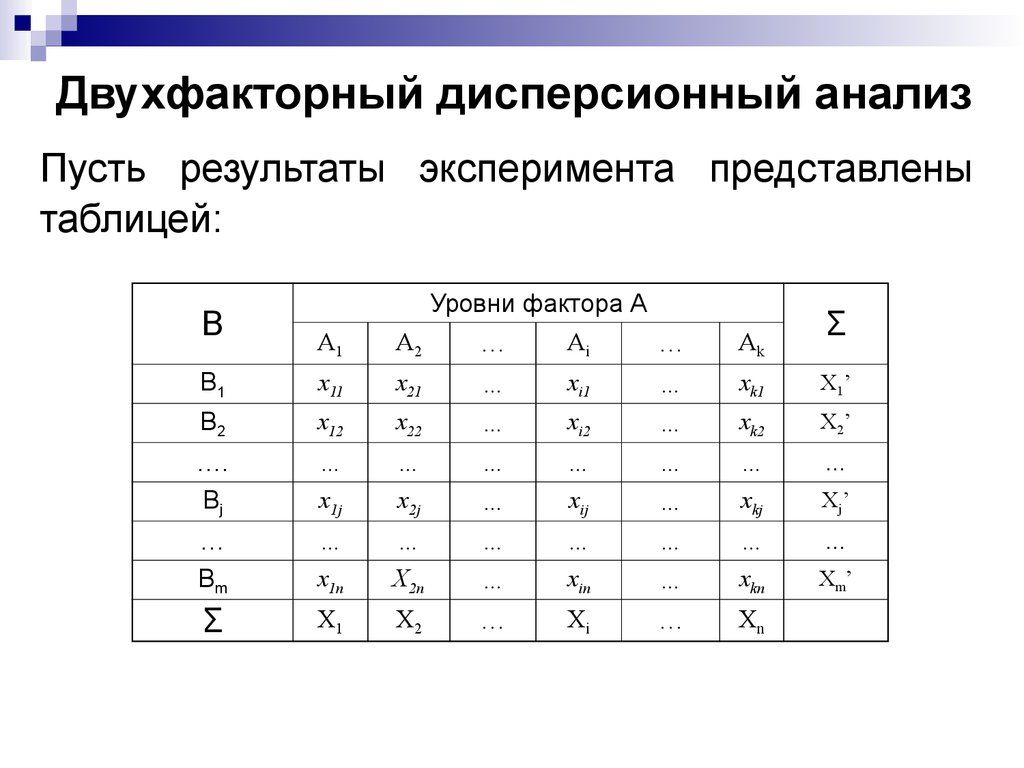
39. Двухфакторный дисперсионный анализ

Пусть результаты эксперимента представлены
таблицей:
A1
Уровни фактора A
A2
Ai
…
…
Ak
B1
x11
x21
…
xi1
…
xk1
X1’
B2
x12
x22
…
xi2
…
xk2
X2’
….
Bj
…
x1j
…
x2j
…
…
xij
…
…
xkj
…
…
Bm
…
x1n
…
X2n
…
…
…
…
xin
…
…
xkn
Σ
X1
X2
…
Xi
…
Xn
B
…
…
Σ
Xj’
…
Xm’

40. Двухфакторный дисперсионный анализ

Дисперсионный анализ для двухфакторных
таблиц
проводится
в
следующей
последовательности. Вычисляются суммы:
k m
Q1
i 1 j 1
2
xij
1 k 2
Q2 X i
m i 1
1 m 2
Q3 X j
k j 1
Далее находятся оценки дисперсий:
2
S0
Q1 Q4 Q2 Q3
(k 1)(m 1)
2
SA
Q2 Q4
k 1
2
SB
Q3 Q4
m 1
2
SA
Если
F ( f1 , f 2 ) , то влияние фактора A признается
2
S0
значимым.
S B2
Если
F ( f1 , f 2 )
2
S0
значимым.
2
1
1 k
X /
Q4
Xi
mk i 1 mk j 1 j
k
, то влияние фактора B признается
2

41. Двухфакторный дисперсионный анализ

Приведенный анализ предполагает независимость факторов A и B.
Если они зависимы, то взаимодействие факторов C=AB также является
фактором, которому соответствует своя дисперсия. Для того чтобы
выделить
такое
взаимодействие,
необходимы
параллельные
наблюдения в каждой клетке таблицы, т.е. при каждом сочетании
факторов A и B на уровнях Ai и Bj соответственно необходимо не одно
наблюдение, а серия наблюдений.
Для оценки влияния взаимодействия факторов AB вычисляем
k m n
дополнительную сумму: Q
x2
5
i 1 j 1 v 1
ijv
Далее анализ проводится, как и ранее, с той лишь разницей, что в
клетках таблицы вместо отдельных значений используется их средние
значения. Вычисляется оценка дисперсии и проверяется значимость
взаимодействия факторов:
2
S AB
Q nQ1
5
mk (n 1)
2
nS0
2
S AB
F ( f1 , f 2 )
f1 (k 1)(m 1)
f 2 mk (n 1)

42. Планирование эксперимента при дисперсионном анализе

Дисперсионный анализ тесно связан с соответствующим
планированием
эксперимента.
Удачно
спланированный
эксперимент, выявляя все необходимые эффекты, оказывается
всегда либо более точным, либо менее трудоемким по
сравнению с непродуманным экспериментом.
Если на результат эксперимента действуют одновременно
несколько факторов, то наилучший эффект дает одновременный
дисперсионный анализ всех этих факторов (многофакторный
анализ).
Методы дисперсионного анализа позволяют исследовать и такой
случай, когда некоторые сочетания уровней пропущены. Такой
эксперимент называется дробным факторным экспериментом
(ДФЭ). Планирование при ДФЭ приобретает особо важную роль,
ибо пропущенные сочетания уровней не так-то просто
нейтрализовать.

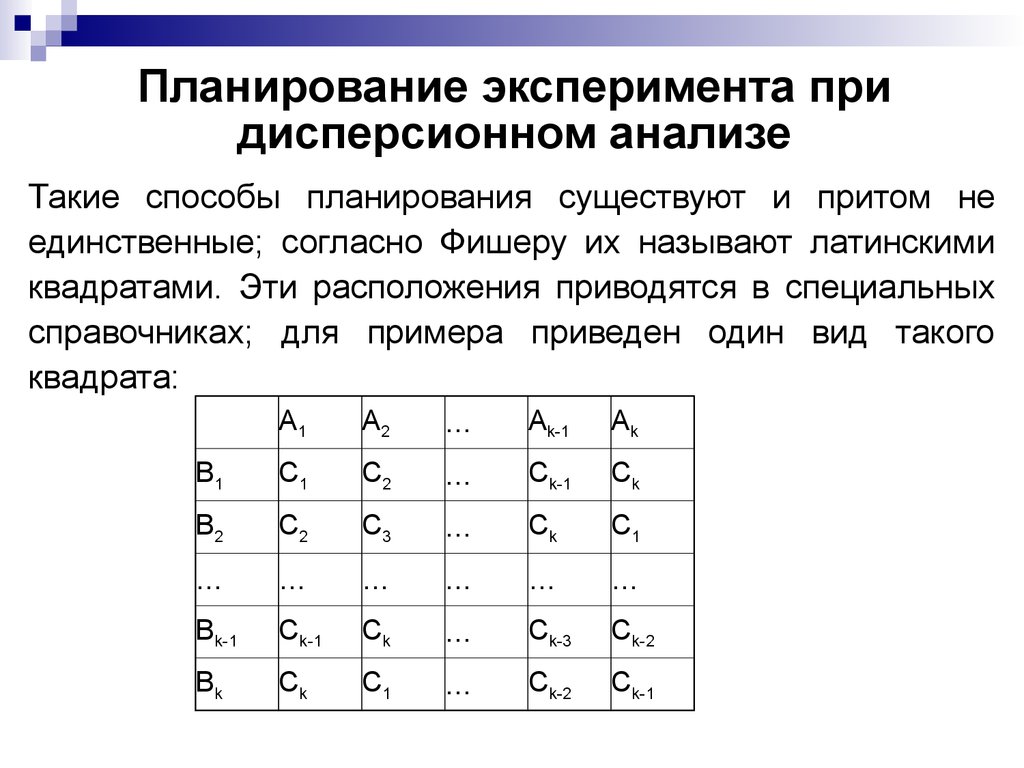
43. Планирование эксперимента при дисперсионном анализе

Такие способы планирования существуют и притом не
единственные; согласно Фишеру их называют латинскими
квадратами. Эти расположения приводятся в специальных
справочниках; для примера приведен один вид такого
квадрата:
A1
A2
…
Ak-1
Ak
B1
C1
C2
…
Ck-1
Ck
B2
C2
C3
…
Ck
C1
…
…
…
…
…
…
Bk-1
Ck-1
Ck
…
Ck-3
Ck-2
Bk
Ck
C1
…
Ck-2
Ck-1

44. Планирование эксперимента при дисперсионном анализе

k k
Схема расчетов для латинского квадрата
2
Q1 xij
очень похожа на обычный двухфакторный
i 1 j 1
анализ:
Находим сумму квадратов по столбцам,
1 k 2
Q2 X i
k i 1
деленную на число наблюдений в столбце:
Находим сумму квадратов итогов по строкам,
1 k 2
Q3 X j
k j 1
деленную на число наблюдений в строке:
2
2
Находим квадрат общего итога, деленный на
1 k
1 k
Q4 2 X i 2 X j
число всех наблюдений:
k i 1 k j 1
Находим сумму квадратов итогов по уровням
1 k 2
Q5 Y
фактора C, деленную на число уровней:
k 1

45. Планирование эксперимента при дисперсионном анализе

Перейдем теперь к вычислению и оценке значимости
дисперсий:
S02
2
SA
Q1 2Q4 Q2 Q3 Q5
(k 1)( k 2)
Q 2 Q 4 2 Q3 Q4
, SB
k 1
k 1
2
2
2
2
2
2
S A S0
S S
2
2
Если отличие будет значимым, то
A, B 0 B
k
k
Q Q4
2
SC 5
k 1
SC S 0
2
Если отличие будет значимым, то
C
k