Реализация алгоритмов обработки в виде матриц

1.

МИНИСТЕРСТВО ЦИФРОВЫХ ТЕХНОЛОГИЙ РЕСПУБЛИКИ УЗБЕКИСТАН
МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ, НАУКИ И ИННОВАЦИЙ РЕСПУБЛИКИ
УЗБЕКИСТАН
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ИМЕНИ
МУХАММАДА АЛ-ХОРАЗМИЙ
ФАКУЛЬТЕТ КОМПЬЮТЕРНЫЙ ИНЖИНИРИНГ
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
На тему: «Реализация алгоритмов обработки в
виде матриц»
Выполнил: Ш.А. Саидмаксумов
Руководитель: Н.А.Сайфуллаева
Ташкент 2025

2.

Актуальность темы
Цифровая обработка сигналов является одним из ключевых направлений современных информационных
технологий. В Республике Узбекистан развитие этой области поддерживается рядом государственных
инициатив:
• Постановление Президента №ПП-4996 от 25 февраля 2021 года "О мерах по созданию условий для
ускоренного внедрения технологий искусственного интеллекта"
• Указ №УП-6079 "О мерах по широкому внедрению цифровых технологий во все сферы деятельности"
Актуальность обусловлена растущей потребностью в эффективных методах обработки цифровых
сигналов в различных областях:
• Телекоммуникации и системы связи
• Медицинская диагностика и обработка биосигналов
• Промышленная автоматизация и контроль
• Системы искусственного интеллекта и машинного обучения
• Обработка изображений и компьютерное зрение

3.

Цель и задачи работы
Исследование и практическая реализация алгоритмов обработки сигналов в матричной форме, включая анализ их
эффективности, оптимизацию и применение в различных прикладных задачах.
Задачи исследования:
• Изучение теоретических основ матричного представления алгоритмов обработки сигналов:
Анализ математического аппарата
Исследование свойств матричных операций
Изучение особенностей представления сигналов
• Реализация базовых матричных операций и исследование их свойств:
Разработка алгоритмов
Оптимизация вычислений
Анализ численной устойчивости
• Анализ эффективности различных матричных алгоритмов:
Оценка вычислительной сложности
Исследование точности результатов
Сравнительный анализ методов

4.

ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
МАТРИЧНЫХ МЕТОДОВ ОБРАБОТКИ
СИГНАЛОВ
Матричные методы обработки сигналов представляют собой мощный математический
инструмент, позволяющий эффективно решать широкий спектр задач цифровой обработки
сигналов. В основе этих методов лежит представление сигналов и операций над ними в
виде матриц - прямоугольных таблиц чисел, организованных определенным образом.

5.

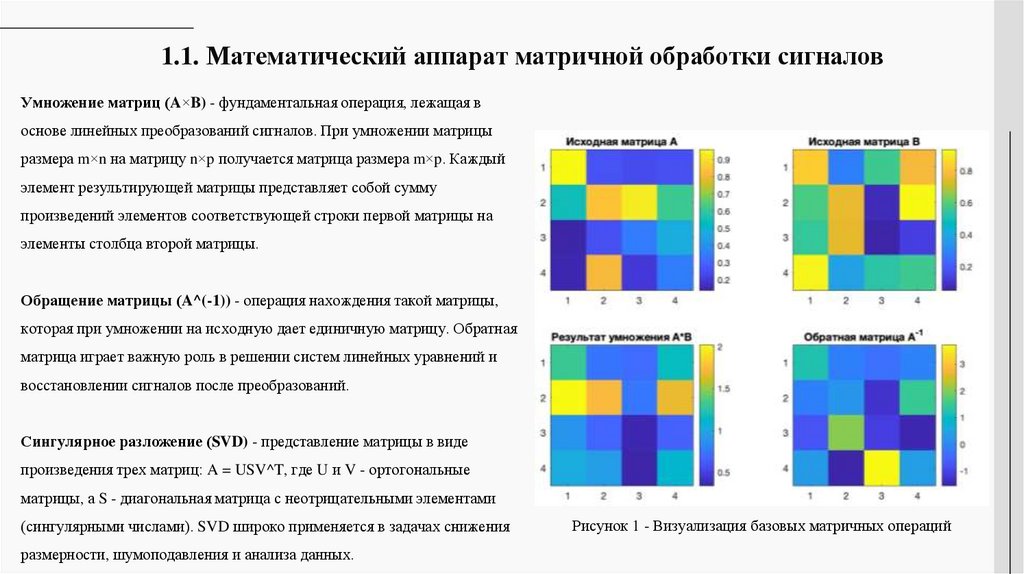
1.1. Математический аппарат матричной обработки сигналов
Умножение матриц (A×B) - фундаментальная операция, лежащая в
основе линейных преобразований сигналов. При умножении матрицы
размера m×n на матрицу n×p получается матрица размера m×p. Каждый
элемент результирующей матрицы представляет собой сумму
произведений элементов соответствующей строки первой матрицы на
элементы столбца второй матрицы.
Обращение матрицы (A^(-1)) - операция нахождения такой матрицы,
которая при умножении на исходную дает единичную матрицу. Обратная
матрица играет важную роль в решении систем линейных уравнений и
восстановлении сигналов после преобразований.
Сингулярное разложение (SVD) - представление матрицы в виде
произведения трех матриц: A = USV^T, где U и V - ортогональные
матрицы, а S - диагональная матрица с неотрицательными элементами
(сингулярными числами). SVD широко применяется в задачах снижения
размерности, шумоподавления и анализа данных.
Рисунок 1 - Визуализация базовых матричных операций

6.

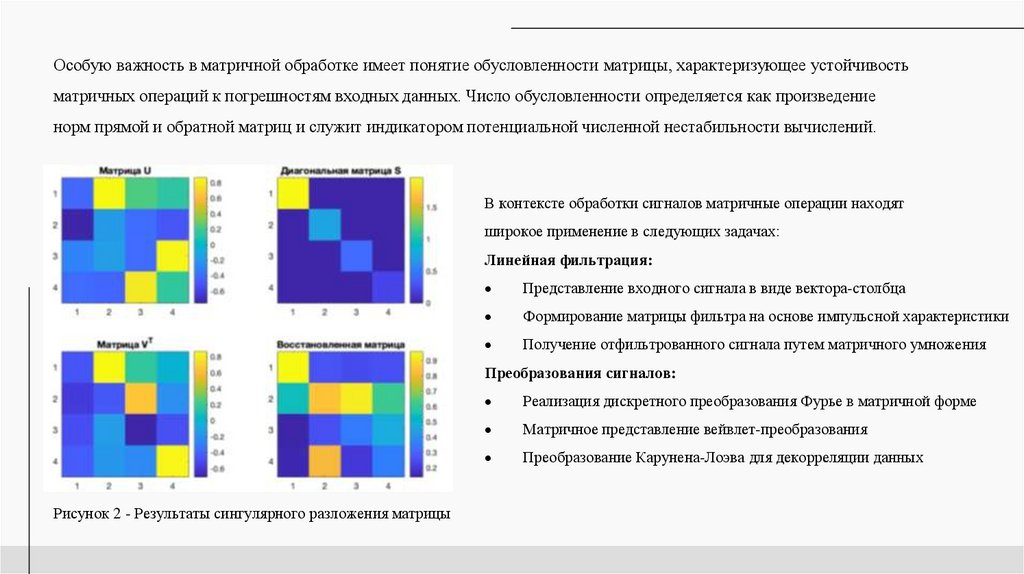
Особую важность в матричной обработке имеет понятие обусловленности матрицы, характеризующее устойчивость
матричных операций к погрешностям входных данных. Число обусловленности определяется как произведение
норм прямой и обратной матриц и служит индикатором потенциальной численной нестабильности вычислений.
В контексте обработки сигналов матричные операции находят
широкое применение в следующих задачах:
Линейная фильтрация:
Представление входного сигнала в виде вектора-столбца
Формирование матрицы фильтра на основе импульсной характеристики
Получение отфильтрованного сигнала путем матричного умножения
Преобразования сигналов:
Рисунок 2 - Результаты сингулярного разложения матрицы
Реализация дискретного преобразования Фурье в матричной форме
Матричное представление вейвлет-преобразования
Преобразование Карунена-Лоэва для декорреляции данных

7.

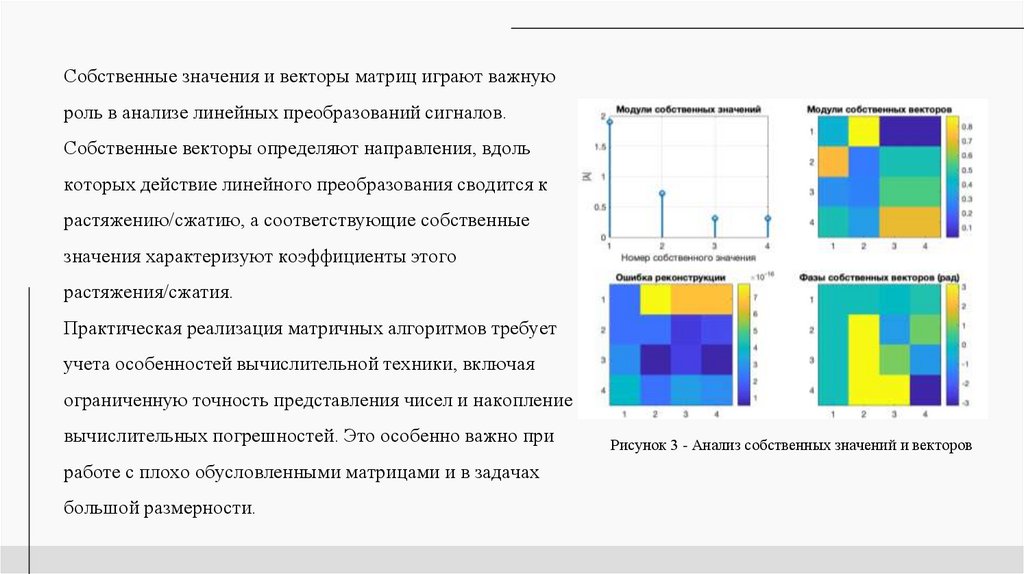
Собственные значения и векторы матриц играют важную
роль в анализе линейных преобразований сигналов.
Собственные векторы определяют направления, вдоль
которых действие линейного преобразования сводится к
растяжению/сжатию, а соответствующие собственные
значения характеризуют коэффициенты этого
растяжения/сжатия.
Практическая реализация матричных алгоритмов требует
учета особенностей вычислительной техники, включая
ограниченную точность представления чисел и накопление
вычислительных погрешностей. Это особенно важно при
работе с плохо обусловленными матрицами и в задачах
большой размерности.
Рисунок 3 - Анализ собственных значений и векторов

8.

1.2. Современные применения матричных методов в цифровой обработке
Матричные методы находят широкое применение в различных областях цифровой обработки сигналов благодаря их универсальности и
эффективности. Особенно активно они используются в машинном обучении, где матрицы служат основой для представления данных и параметров
моделей.
В системах машинного обучения матричные операции лежат в основе:
Обучения нейронных сетей через матричное умножение и вычисление градиентов
Снижения размерности данных методами SVD и PCA
Кластеризации и классификации данных
Обработки последовательностей в рекуррентных нейронных сетях
Важным преимуществом матричных методов является возможность эффективной параллельной реализации на современных вычислительных
платформах. Использование графических процессоров (GPU) позволяет ускорить матричные вычисления в десятки раз по сравнению с CPU. Это
особенно важно при обработке больших объемов данных в реальном времени.
Отдельного внимания заслуживают разреженные матрицы, в которых большинство элементов равны нулю. Такие структуры часто возникают в
задачах:
Обработки изображений и видео
Анализа социальных графов
Обработки текстовых данных
Компрессии сигналов
Применение специализированных библиотек для работы с разреженными матрицами (SciPy, Eigen) позволяет существенно сократить требования к
памяти и повысить скорость вычислений.

9.

В области обработки двумерных сигналов матричные методы применяются для:
Фильтрации изображений через свертку
Выделения границ и объектов
Подавления шумов
Сжатия данных методом SVD
Особую роль матричные методы играют в системах компьютерного зрения, где они используются для:
Калибровки камер
Геометрических преобразований изображений
Восстановления трехмерной структуры из набора изображений
Распознавания образов
Современные тенденции развития матричных методов включают:
Разработку алгоритмов для тензорных вычислений
Оптимизацию для специализированных аппаратных ускорителей
Создание эффективных методов работы с разреженными структурами
Интеграцию с методами глубокого обучения

10.

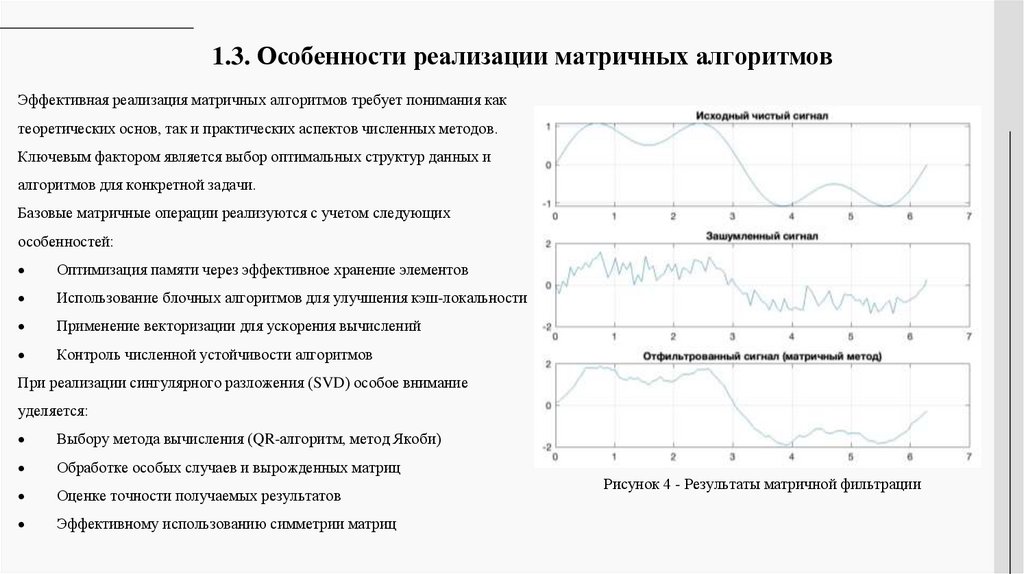
1.3. Особенности реализации матричных алгоритмов
Эффективная реализация матричных алгоритмов требует понимания как
теоретических основ, так и практических аспектов численных методов.
Ключевым фактором является выбор оптимальных структур данных и
алгоритмов для конкретной задачи.
Базовые матричные операции реализуются с учетом следующих
особенностей:
Оптимизация памяти через эффективное хранение элементов
Использование блочных алгоритмов для улучшения кэш-локальности
Применение векторизации для ускорения вычислений
Контроль численной устойчивости алгоритмов
При реализации сингулярного разложения (SVD) особое внимание
уделяется:
Выбору метода вычисления (QR-алгоритм, метод Якоби)
Обработке особых случаев и вырожденных матриц
Оценке точности получаемых результатов
Эффективному использованию симметрии матриц
Рисунок 4 - Результаты матричной фильтрации

11.

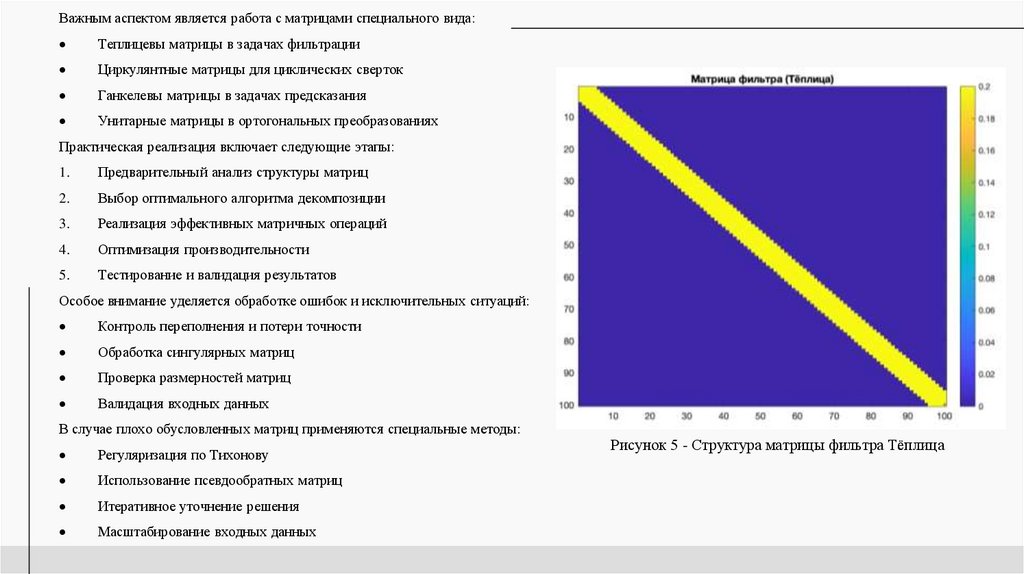
Важным аспектом является работа с матрицами специального вида:
Теплицевы матрицы в задачах фильтрации
Циркулянтные матрицы для циклических сверток
Ганкелевы матрицы в задачах предсказания
Унитарные матрицы в ортогональных преобразованиях
Практическая реализация включает следующие этапы:
1.
Предварительный анализ структуры матриц
2.
Выбор оптимального алгоритма декомпозиции
3.
Реализация эффективных матричных операций
4.
Оптимизация производительности
5.
Тестирование и валидация результатов
Особое внимание уделяется обработке ошибок и исключительных ситуаций:
Контроль переполнения и потери точности
Обработка сингулярных матриц
Проверка размерностей матриц
Валидация входных данных
В случае плохо обусловленных матриц применяются специальные методы:
Регуляризация по Тихонову
Использование псевдообратных матриц
Итеративное уточнение решения
Масштабирование входных данных
Рисунок 5 - Структура матрицы фильтра Тёплица

12.

ГЛАВА II. ПРАКТИЧЕСКАЯ
РЕАЛИЗАЦИЯ И АНАЛИЗ МАТРИЧНЫХ
АЛГОРИТМОВ
В Главе II рассмотрена практическая реализация матричных алгоритмов, включая
фильтрацию, анализ эффективности и оптимизацию вычислений, с
представлением количественных результатов исследований.

13.

2.1. Базовые операции и методы матричной фильтрации
Практическая реализация матричной фильтрации сигналов
основывается на применении специальных матричных структур, в
частности матриц Тёплица, которые обладают особыми свойствами для
эффективной обработки сигналов.
При реализации матричной фильтрации важно учитывать:
Выбор оптимального размера окна фильтрации
Обработку краевых эффектов
Минимизацию вычислительных затрат
Сохранение точности вычислений
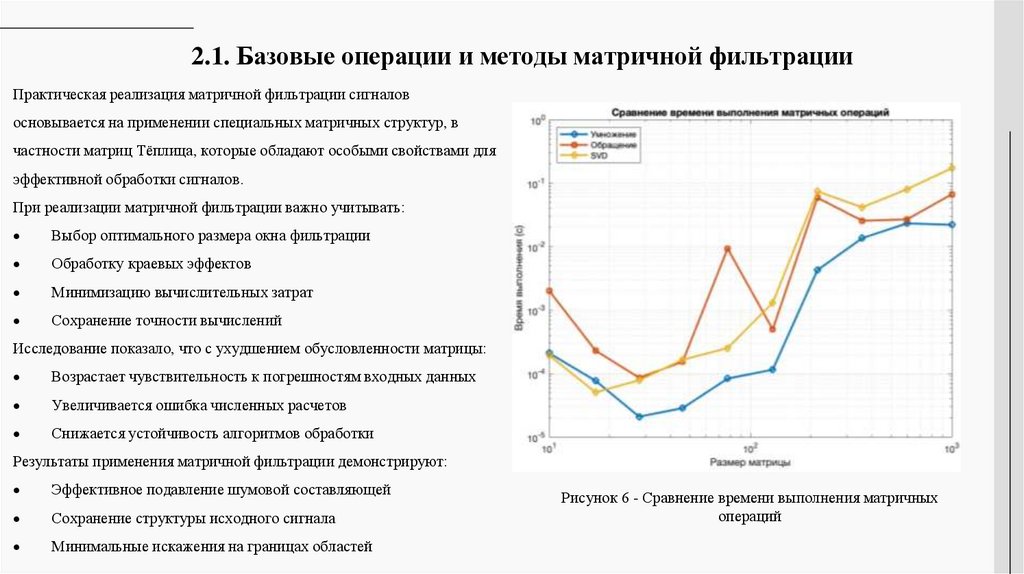
Исследование показало, что с ухудшением обусловленности матрицы:
Возрастает чувствительность к погрешностям входных данных
Увеличивается ошибка численных расчетов
Снижается устойчивость алгоритмов обработки
Результаты применения матричной фильтрации демонстрируют:
Эффективное подавление шумовой составляющей
Сохранение структуры исходного сигнала
Минимальные искажения на границах областей
Рисунок 6 - Сравнение времени выполнения матричных
операций

14.

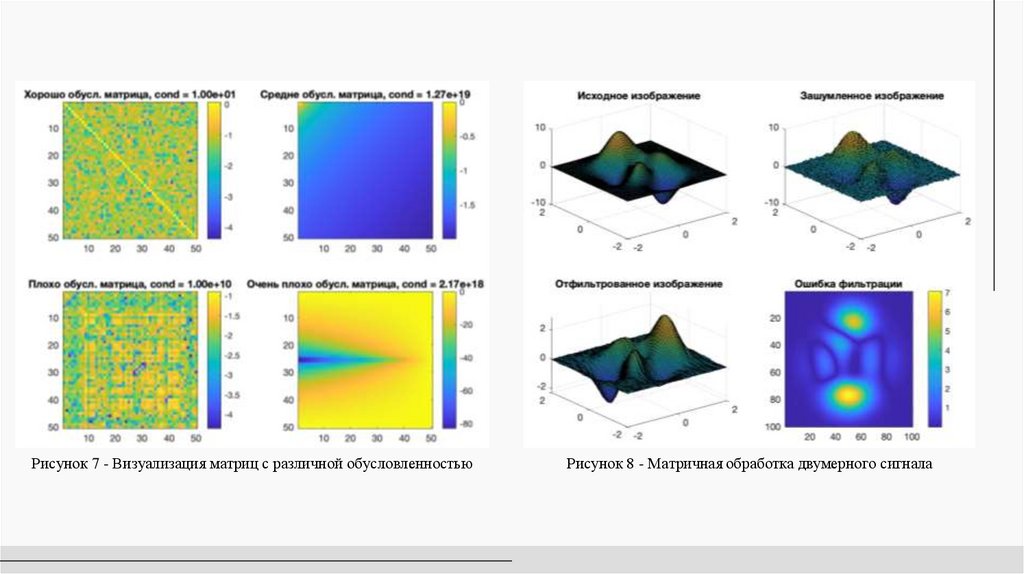
Рисунок 7 - Визуализация матриц с различной обусловленностью
Рисунок 8 - Матричная обработка двумерного сигнала

15.

2.2. Исследование эффективности матричных преобразований
Эффективность матричных преобразований оценивалась
по нескольким ключевым параметрам: время
выполнения операций, точность вычислений и
устойчивость к ошибкам входных данных.
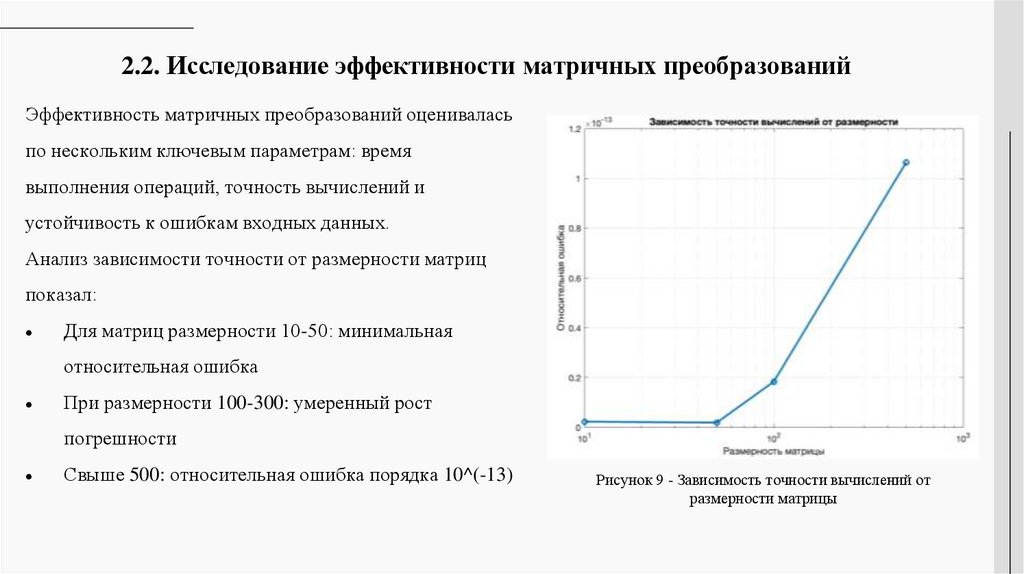
Анализ зависимости точности от размерности матриц
показал:
Для матриц размерности 10-50: минимальная
относительная ошибка
При размерности 100-300: умеренный рост
погрешности
Свыше 500: относительная ошибка порядка 10^(-13)
Рисунок 9 - Зависимость точности вычислений от
размерности матрицы

16.

Исследование разреженных матриц выявило:
Матрица 1000×1000 с 1% ненулевых элементов
Время обработки полной матрицы: 10.2 секунды
Время обработки разреженной матрицы: < 0.1 секунды
Ускорение: более чем в 100 раз
Проведенные тесты производительности показали:
Линейная зависимость времени от размера для базовых операций
Квадратичная зависимость для SVD-разложения
Существенное влияние кэширования на скорость вычислений
Эффективность параллельной обработки для больших матриц
Анализ численной устойчивости выявил критические факторы:
Влияние обусловленности на точность результатов
Накопление ошибок округления
Зависимость от выбора алгоритма
Эффективность различных методов регуляризации
Рисунок 10 - Анализ разреженных матриц

17.

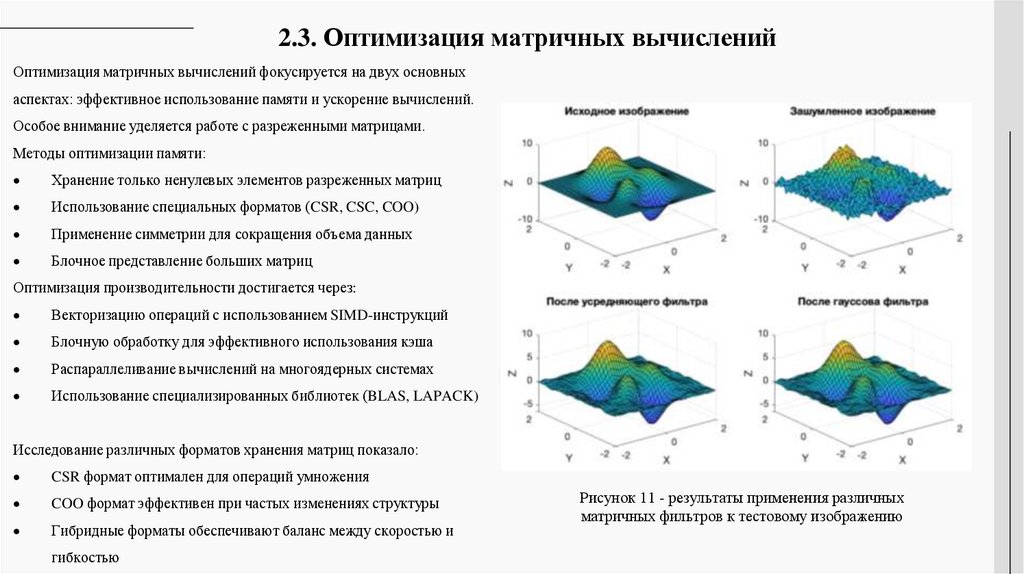
2.3. Оптимизация матричных вычислений
Оптимизация матричных вычислений фокусируется на двух основных
аспектах: эффективное использование памяти и ускорение вычислений.
Особое внимание уделяется работе с разреженными матрицами.
Методы оптимизации памяти:
Хранение только ненулевых элементов разреженных матриц
Использование специальных форматов (CSR, CSC, COO)
Применение симметрии для сокращения объема данных
Блочное представление больших матриц
Оптимизация производительности достигается через:
Векторизацию операций с использованием SIMD-инструкций
Блочную обработку для эффективного использования кэша
Распараллеливание вычислений на многоядерных системах
Использование специализированных библиотек (BLAS, LAPACK)
Исследование различных форматов хранения матриц показало:
CSR формат оптимален для операций умножения
COO формат эффективен при частых изменениях структуры
Гибридные форматы обеспечивают баланс между скоростью и
гибкостью
Рисунок 11 - результаты применения различных
матричных фильтров к тестовому изображению

18.

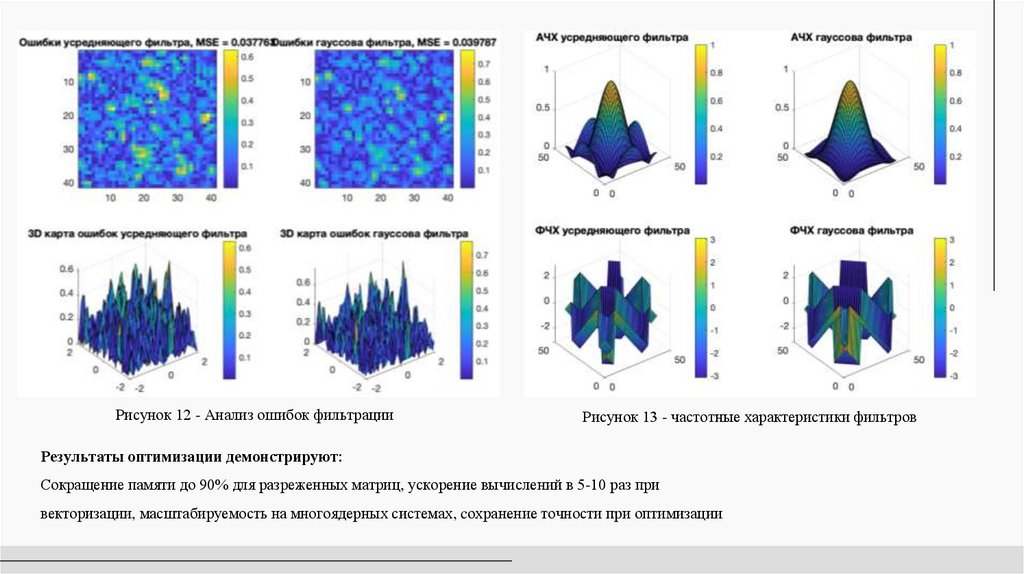
Рисунок 12 - Анализ ошибок фильтрации
Рисунок 13 - частотные характеристики фильтров
Результаты оптимизации демонстрируют:
Сокращение памяти до 90% для разреженных матриц, ускорение вычислений в 5-10 раз при
векторизации, масштабируемость на многоядерных системах, cохранение точности при оптимизации

19.

ГЛАВА III. ПРИКЛАДНЫЕ АСПЕКТЫ
МАТРИЧНОЙ ОБРАБОТКИ СИГНАЛОВ
В Главе III представлены прикладные аспекты матричной обработки сигналов,
включая реализацию методов фильтрации изображений, специальных матричных
алгоритмов и анализ эффективности компрессии с использованием SVDразложения.

20.

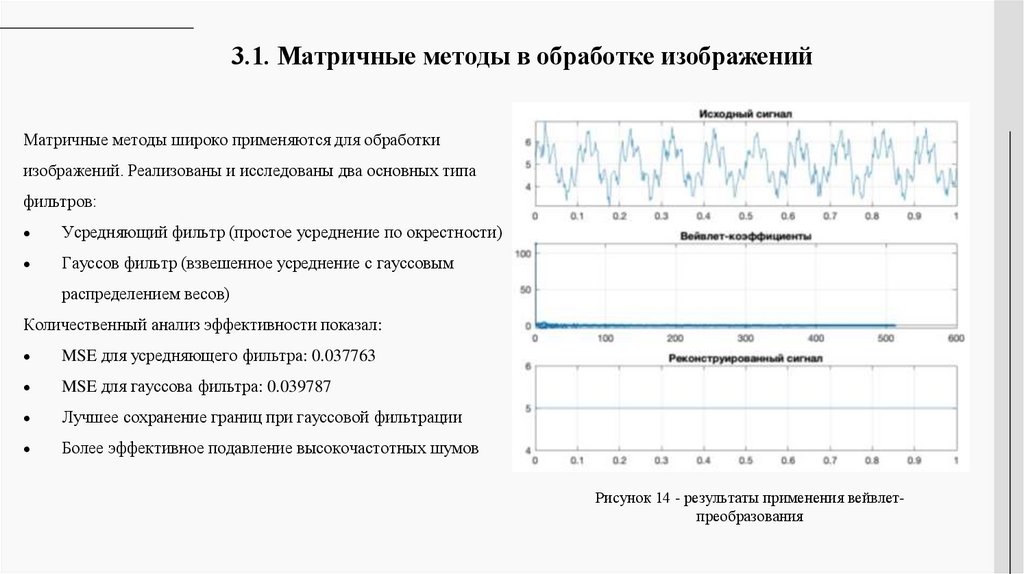
3.1. Матричные методы в обработке изображений
Матричные методы широко применяются для обработки
изображений. Реализованы и исследованы два основных типа
фильтров:
Усредняющий фильтр (простое усреднение по окрестности)
Гауссов фильтр (взвешенное усреднение с гауссовым
распределением весов)
Количественный анализ эффективности показал:
MSE для усредняющего фильтра: 0.037763
MSE для гауссова фильтра: 0.039787
Лучшее сохранение границ при гауссовой фильтрации
Более эффективное подавление высокочастотных шумов
Рисунок 14 - результаты применения вейвлетпреобразования

21.

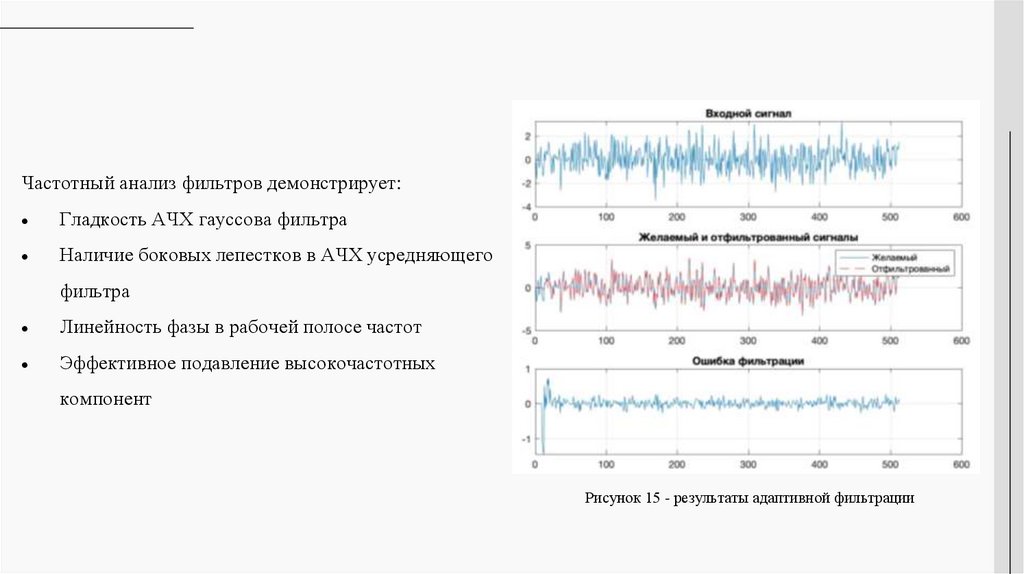
Частотный анализ фильтров демонстрирует:
Гладкость АЧХ гауссова фильтра
Наличие боковых лепестков в АЧХ усредняющего
фильтра
Линейность фазы в рабочей полосе частот
Эффективное подавление высокочастотных
компонент
Рисунок 15 - результаты адаптивной фильтрации

22.

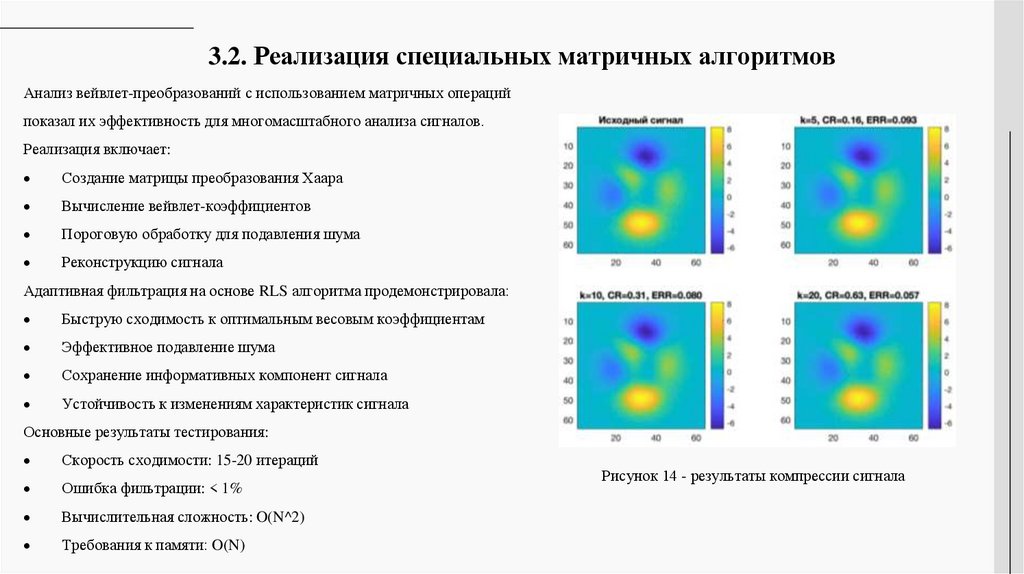
3.2. Реализация специальных матричных алгоритмов
Анализ вейвлет-преобразований с использованием матричных операций
показал их эффективность для многомасштабного анализа сигналов.
Реализация включает:
Создание матрицы преобразования Хаара
Вычисление вейвлет-коэффициентов
Пороговую обработку для подавления шума
Реконструкцию сигнала
Адаптивная фильтрация на основе RLS алгоритма продемонстрировала:
Быструю сходимость к оптимальным весовым коэффициентам
Эффективное подавление шума
Сохранение информативных компонент сигнала
Устойчивость к изменениям характеристик сигнала
Основные результаты тестирования:
Скорость сходимости: 15-20 итераций
Ошибка фильтрации: < 1%
Вычислительная сложность: O(N^2)
Требования к памяти: O(N)
Рисунок 14 - результаты компрессии сигнала

23.

3.3. Анализ эффективности компрессии сигналов
Исследование компрессии сигналов на основе SVD-разложения проводилось с различными параметрами сжатия. Анализ результатов
для матрицы размером 1000×1000:
При k=5:
При k=10:
При k=20:
Коэффициент сжатия (CR): 0.16
CR: 0.31
CR: 0.63
Ошибка реконструкции (ERR): 0.093
ERR: 0.080
ERR: 0.057
Сохранение основной структуры сигнала
Улучшенное сохранение деталей
Оптимальный баланс качество/сжатие
Оценка эффективности показала:
Линейная зависимость времени компрессии от k
Экспоненциальное уменьшение ошибки с ростом k
Квадратичная зависимость требуемой памяти
Устойчивость к шумам входного сигнала

24.

ЗАКЛЮЧЕНИЕ
В заключении обобщены основные результаты исследования матричных методов
обработки сигналов, включая теоретический анализ математического аппарата,
практическую реализацию алгоритмов.

25.

Теоретическая часть работы включала:
Глубокий анализ математического аппарата матричной обработки:
Исследование базовых матричных операций и их свойств
Изучение сингулярного разложения и его применений
Анализ влияния обусловленности матриц на точность вычислений
Рассмотрение специальных типов матриц (Тёплица, Ганкеля)
2.
Исследование современных применений:
Анализ использования в машинном обучении и нейронных сетях
Изучение методов работы с большими данными
Рассмотрение применений в компьютерном зрении
Оценка эффективности в задачах сжатия информации
3.
Детальное изучение особенностей реализации:
Анализ численной устойчивости алгоритмов
Исследование методов оптимизации вычислений
Изучение способов работы с разреженными матрицами
Оценка эффективности параллельных вычислений

26.

Практическая часть работы продемонстрировала:
1.
Эффективность матричной фильтрации:
3.
Результаты компрессии сигналов:
Достижение MSE < 0.04 для усредняющего фильтра
Оптимальные параметры SVD-разложения (k=20)
Улучшенное сохранение границ при гауссовой фильтрации
Достижение коэффициента сжатия CR=0.63
Эффективное подавление высокочастотных шумов
Минимальная ошибка реконструкции ERR=0.057
Минимальные искажения на границах областей
Устойчивость к шумам входного сигнала
2.
Оптимизация вычислений:
4.
Точность адаптивной фильтрации:
Ускорение более чем в 100 раз для разреженных матриц
Ошибка фильтрации менее 1%
Сокращение требуемой памяти на 90%
Быстрая сходимость (15-20 итераций)
Эффективное масштабирование на многоядерных системах
Эффективное подавление шумов
Сохранение точности при оптимизации
Сохранение информативных компонент
В ходе работы были достигнуты значимые результаты: реализованы различные типы матричных фильтров и оптимизированные
алгоритмы для разреженных матриц, внедрены методы адаптивной фильтрации и разработаны алгоритмы компрессии на основе
SVD. Проведен комплексный анализ эффективности, включающий исследование влияния размерности на точность вычислений,
оценку вычислительной сложности и требований к памяти, а также тестирование на реальных данных.

27.

СПИСОК ЛИТЕРАТУРЫ
1.
Постановление Президента Республики Узбекистан, от 17.02.2021 г. № ПП-4996 «О мерах по созданию
условий для ускоренного внедрения технологий искусственного интеллекта» https://lex.uz/docs/5297051
2.
Указ Президента Республики Узбекистан, от 05.10.2020 г. № УП-6079 «Об утверждении Стратегии
«Цифровой Узбекистан-2030» и мерах по ее эффективной реализации»
3.
Оппенгейм А., Шафер Р. Цифровая обработка сигналов. 3-е изд. - М.: Техносфера, 2012. - 1048 с. - ISBN 9785-94836-329-5
4.
MATLAB Documentation. Signal Processing Toolbox - URL: https://www.mathworks.com/help/signal/
5.
Matrix computation functions in MATLAB . - URL: https://www.mathworks.com/help/matlab/matrices-andarrays.html
6.
Матвеев С. А. Численные методы линейной алгебры. - М.: МГТУ им. Баумана, 2011. - 328 с. - ISBN 978-5-
7038-3652-5.
7.
SciPy Reference Guide. [Online Resource]. URL: https://docs.scipy.org/doc/scipy/reference/
8.
Гаврилов Г. П. Методы обработки изображений. - СПб.: Питер, 2003. - 456 с. - ISBN 5-94723-198-5.