Похожие презентации:
Перестановки. Урок №1
1.
Урок №1.Тема урока :
«Перестановки».
2.
Сколько различных т рехзначныхчисел можно записат ь с помощью
трёх цифр: 3,5,7 не повт оряя их?
Решение:
357,375,537,573,735,753.
Таких чисел будет 6.
Добавим к данным трем цифрам ещё одну,
например 8. Тогда задача примет вид:
3.
Сколько различных чет ырехзначныхчисел можно записат ь с помощью
цифр 3,5,7,8, не повт оряя их?
357
8357
3857
3587
3578
375
8375
3875
3785
3758
Всего будет 24:
537
573
735
753
8537 8573 8735 8753
5837 5873 7835 7853
5387 5783 7385 7583
5378 5738 7358 7538
4.
Сколькими различными способамиможно посадит ь за ст олом чет ырёх
человек, если к эт ому ст олу
прист авлены чет ыре ст ула?
По существу эта задача не
отличается от предыдущей о
четырех цифрах, поэтому и ответ
будет тот же – 24.
5.
Пусть дано произвольное множествоиз n элементов. Упорядочить
множество – значит поставить
какой-либо элемент множества на
первое место, какой-либо другой –
на второе и т.д., пока не останется
последний элемент, который
займёт последнее, n- е место.
6.
Мы установили, это множество из трёх цифрможно упорядочить шестью способами, а
множество из четырёх цифр-24 .
ВОПРОС:
Сколькими способами можно
упорядочить множество из n
элементов, где n- любое
натуральное число?
7.
Каждый способ упорядочения множества каких либоэлементов называется
перест ановкой этих
элементов.
8.
Теорема: Число перестановок из nэлементов равно произведению n
первых натуральных чисел, т.е.
1·2·3...n.
Произведение n первых натуральных
чисел обозначают n!
Например: 1! = 1;
2! = 1·2 = 2;
3! = 1·2·3 = 6; 4! = 1·2·3·4 = 24.
Принято считать,что
9.
Задача №1.Сколькими способами можно
составить список из 9 учеников?
Решение:
9! = 1·2·3...8·9 = 362880.
10.
Задача №2Сколькими способами можно
составить маршрут путешествия,
проходящего через 7 городов?
Решение:
7! = 1·2...6·7 = 5040.
11.
Задание№3Вычислите:
г) 5 6! 5! 6
А) 6! -5!
Б) 4! . 2!
8!
В)
6!
.
.
6 . 6!
д)
12!
9! . 3!
12.
Задание №4 Сократите дробьа)
n!
( n 1)!
б)
n!
2!( n 2)!
в)
(n 2)!(n2 9)
(n 4)!
13.
Задание №5 Решите уравнение:(n 2)!
72
n!
Задание №6
Сколько различных пят изначных чисел можно
записат ь с помощью цифр 0,2,4,5,7, не
повт оряя их?











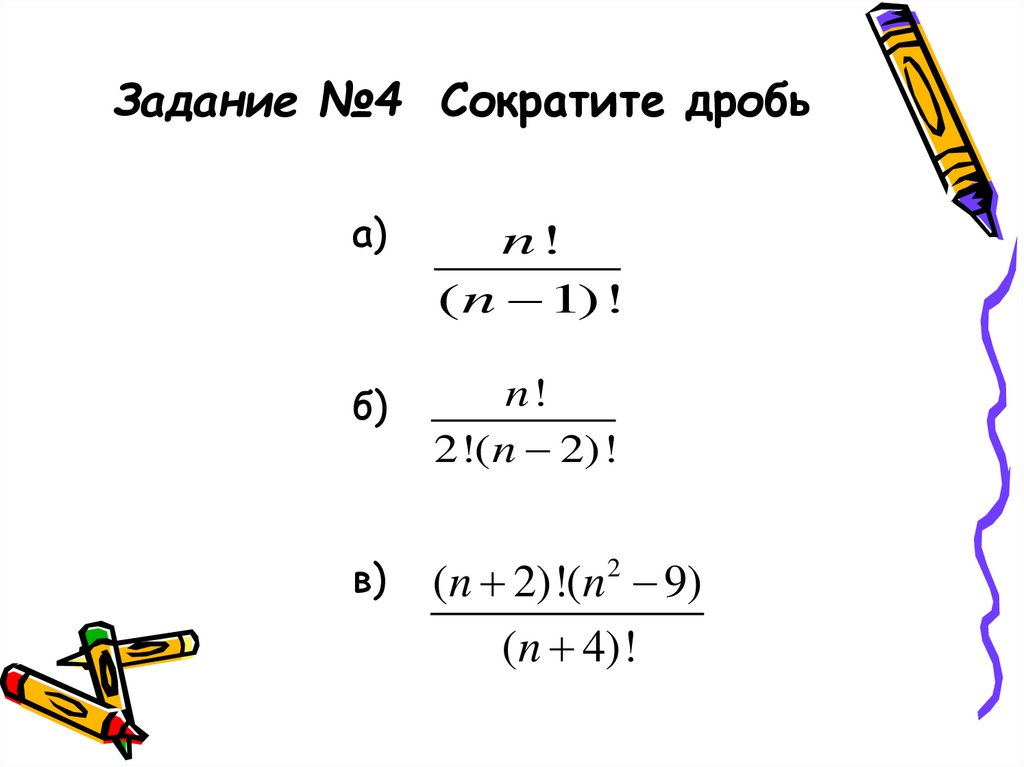

 Математика
Математика








