Похожие презентации:
Перестановки. Факториал
1.
Перестановки. Факториал2.
Некоторые типы комбинаций играют в математике настольковажную роль и встречаются так часто, что для них введены
специальные названия и выведены формулы для подсчёта.
Начнём с комбинаций, которые называются перестановками.
Подсчитаем, сколько существует разных способов каждому из троих людей
присвоить номер от 1 до 3. Тот же самый вопрос можно задать иначе:
сколькими способами можно построить трёх человек в шеренгу?
3.
ПерестановкиПерестановкой из N различных элементов называют комбинацию, в
которой все эти N элементов расположены в определенном
порядке.
Элементами, которые участвуют в перестановке, могут быть числа,
буквы, шары и вообще любые объекты.
Выпишем для примера все перестановки из чисел 1, 2, 3:
123, 132, 213, 231, 312, 321.
Рассмотрим все перестановки из трёх букв a, b, c:
abc, acb, bac, bca, cab, cba.
Можно взять в качестве элементов перестановок три разноцветных
шара
4.
ФакториалКонечно, во всех этих случаях количество перестановок будет одинаковым, ведь оно
зависит только от того, сколько элементов участвует в перестановке. Мы видим, что из
трёх элементов можно составить 6 разных перестановок. Понятно, что из двух элементов
перестановок будет 2.
Выведем общую формулу для количества перестановок из N элементов. Будем
использовать для этого правило умножения. Первый элемент перестановки можно
выбрать N способами; после этого второй элемент —N – 1 способами (поскольку один
элемент уже выбран); третий — N – 2 способами и т. д. до последнего элемента, который
можно будет выбрать только одним способом (это единственный элемент, который ещё
не был выбран). По правилу умножения общее количество комбинаций будет равно
произведению N ∙ (N – 1) ∙ (N – 2) ∙ … ∙ 1.
Мы получили, что количество всех перестановок из N элементов равно произведению
всех натуральных чисел от 1 до N. Это произведение называется в математике
факториалом числа N (от латинского factorialis — «умножающий») и обозначается N!:
N! = 1 2 3 4 ……. N
Отметим также, что значение 0! = 1.
5.
Факториалы чисел от 0 до 10n
n!
0
1
1
1
2
2
3
6
4
24
5
120
6
720
7
5040
8
40320
9
362880
10
3628800
Факториал n! быстро растёт с увеличением n. Поэтому даже для 10
предметов перестановок очень много и выписать все практически
невозможно.
6.
Пример 1Сколько различных пятизначных чисел можно составить из цифр 0, 1, 2, 3,
4, если в каждом числе ни одна цифра не повторяется?
Решение
Из данных пяти цифр можно образовать Р5 = 5! пятизначных чисел. Но так
как среди цифр есть 0, то необходимо исключить те числа, которые
начинаются с него, то есть Р4 = 4! (ноль стоит на первом месте, а
остальные цифры переставляем).
Тогда Р5 - Р4 = 5! - 4! = 120 - 24 = 96
Ответ: 96
7.
Пример 2Сколькими различными способами можно разместить 10 человек вокруг
круглого стола?
Решение
Если бы это было размещение в ряд, то число способов размещения
было бы равно Р10 = 10!. Но так как они сидят за круглым столом, то
сдвиг по окружности относительно центра не считается.
Р10 10!
Тогда
=
= 9! = 362880
10
10
Ответ: 362880
8.
Пример 3Десять групп учатся в десяти размещенных рядом аудиториях. Сколько
существует вариантов размещения групп по аудиториям, при которых
группы № 1 и № 2 будут находиться в соседних аудиториях?
Решение
Условно объединим группы № 1 и № 2 в одну. Тогда способов размещения
будет Р9 . Группы № 1 и № 2 можно поменять между собой местами Р2
способами.
Итак, по правилу произведения:
Р9 ∗ Р2 = 9! ∗ 2! = 362880*2= 725760
Ответ: 725760
9.
Пример 4Сколькими способами можно расставить 4 книжки по алгебре и 3 по
геометрии, чтобы все книжки по геометрии стояли подряд.
Решение
Объединим книжки по геометрии условно в одну. Тогда имеем 5 книг и Р5
перестановок. Книги по геометрии можно расставить между собой Р3
способами. Всего по правилу произведения:
Р5 * Р3 = 5!*3!=120*6=720
Ответ: 720
10.
Пример 5Сколько пятицифровых чисел можно образовать из цифр 1, 2, 3, 4, 5 (без
повторения) так, чтобы четные цифры не стояли рядом?
Решение
Из этих цифр можно образовать Р5 пятицифровых чисел. Среди них есть и
такие, которые содержат 2 и 4 рядом: Р4 ∗ Р2 (смотреть предыдущие две
задачи).
Итак, Р5 − Р4 ∗ Р2 = 120 – 24*2= 72
Ответ: 72
11.
ПРОВЕРЬ СЕБЯ!Выбери правильный ответ:
Сколько различных последовательностей (необязательно осмысленных)
можно составить из букв слова бирка?
12.
Задание 1Сколькими способами можно расставить
8 участников финального забега на 8
беговых дорожках?
Решение
Р8 = 8! = 40 320.
13.
Задание 2Полное собрание сочинений братьев Стругацких включает в
себя 33 тома.
Сколькими способами это собрание можно расставить на
полке?
Решение
Р33 = 33! = 8 683 317 618 811 886 495 518 194 401 280 000 000
14.
Задание 3Вычислите значение дроби:
5!
а) ;
2!
100!
г)
;
99!
7!
б) ;
5!
15!
д)
;
13! ∙ 2!
10!
в) ;
8!
12!
е)
.
3! ∙ 9!
15.
Задание 4Участники лыжных соревнований стартуют с интервалом
в 30 секунд. Чтобы определить порядок старта,
спортсмены тянут жребий, определяющий номер старта.
Сколько существует различных последовательностей
выхода лыжников на старт, если в соревнованиях
принимают участие:
а) 6 лыжников;
б) 8 лыжников;
в) 10 лыжников.
16.
Задание 5Сколько различных последовательностей (не обязательно осмысленных)
можно составить из букв слова:
а) учебник;
б) автор;
в) фонарь;
г) бабуин;
д) кокос.
17.
Задание 6Выпишите все натуральные делители числа: 5!
Решение:
5! = 1*2*3*4*5
Однозначные: 1, 2, 3, 4, 5
Перемножаем по 2: 6, 8, 10, 12, 15, 20
Перемножаем по 3: 24, 30, 40, 60
Перемножаем 4: 120
18.
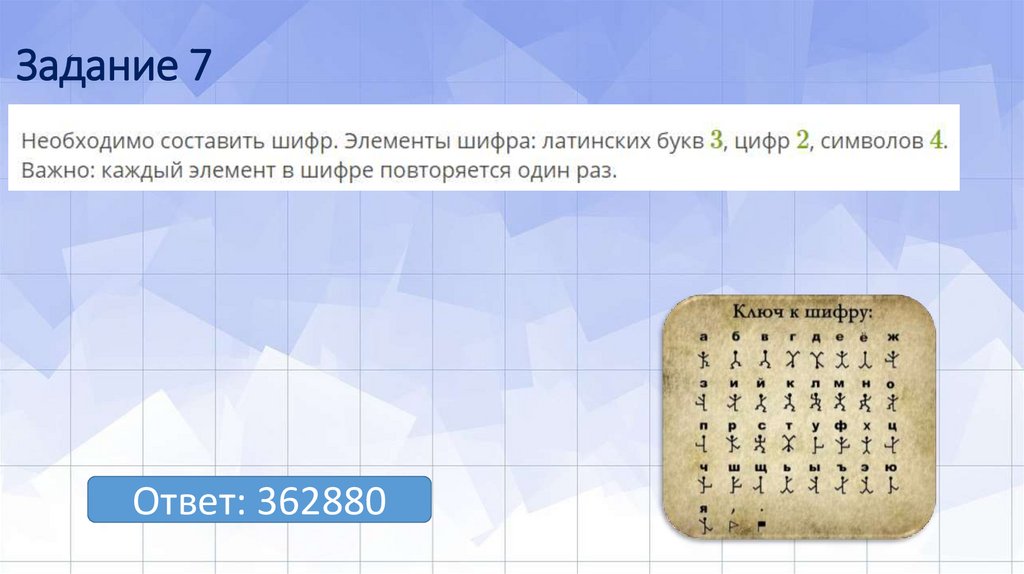
Задание 7Ответ: 362880
19.
Задание 8Сколько различных комбинаций у тренера, если ему необходимо раздать
футболистам номера с 7 по 13?
Ответ: 5040
20.
Заполни пропуски в решении задачи362880
5040
21.
Задание 9Упростите выражения:
Подсказка: n!=1*2*3….*n
(n-2)! = 1*2*3…*(n-2)
(n+1)! = 1*2*3…*(n-2)*(n-1)*n*(n+1)
22.
Домашнее задание:Выучить правила и формулу
1. В автосервис одновременно приехали 4 машины для
ремонта. Сколько существует способов выстроить их в очередь
на обслуживание?
2. Сколько есть способов раздать спортивные номера с 1 – й по
5 – й пяти хоккеистам?
3. Выпишите все натуральные делители числа: 4!
4. Вычислите:
а)
12!
30!
15!
; б)
; в)
;
9!
29!2!
2!16!
г)
14!
;
12!
д)
36!
;
2!34!
25!
23!5!
е)
5. Сколько различных последовательностей (не обязательно
осмысленных) можно составить из букв слова:
а) книга;
б) топот





















 Математика
Математика








