Преобразование НКА с е-переходами в ДКА. Замыкание. Е-Close

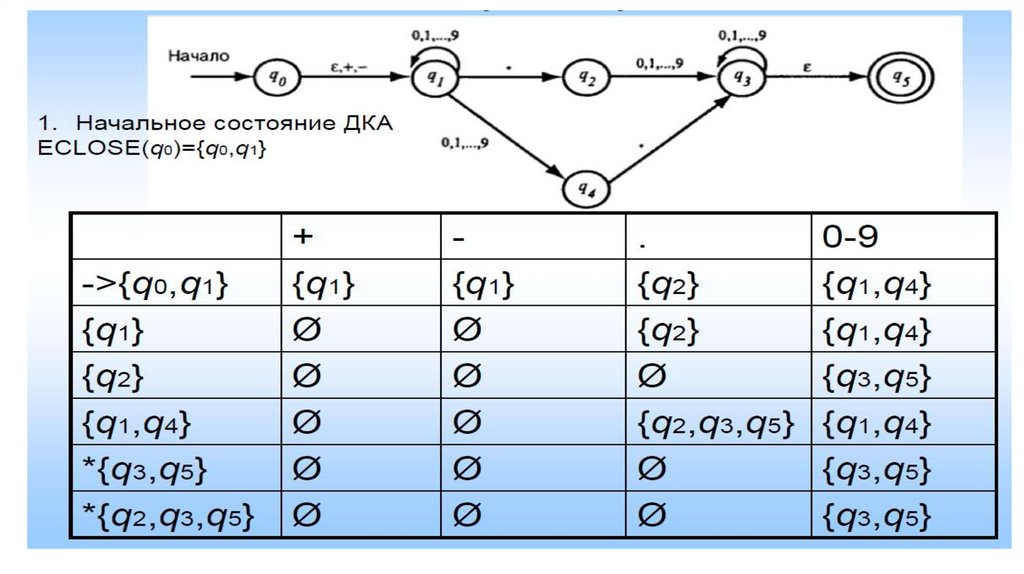
1.

Преобразование НКА с
е-переходами в ДКА.
Замыкание. Е-Close.

2.

Определение
КА = {Q, ∑, δ, q0 , F}, где
Q – конечное мн-во состояний,
∑ - входной алфавит,
δ – правила перехода,
q0 ∈ Q - начальное состояние,
F ∈ Q - конечное мн-во заключительных состояний.

3.

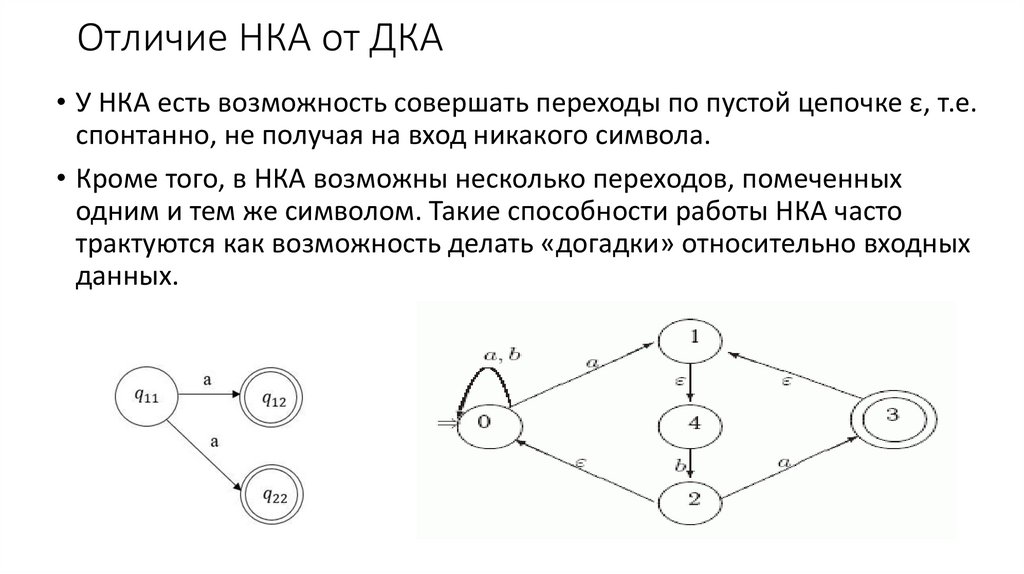
Отличие НКА от ДКА
• У НКА есть возможность совершать переходы по пустой цепочке ε, т.е.
спонтанно, не получая на вход никакого символа.
• Кроме того, в НКА возможны несколько переходов, помеченных
одним и тем же символом. Такие способности работы НКА часто
трактуются как возможность делать «догадки» относительно входных
данных.

4.

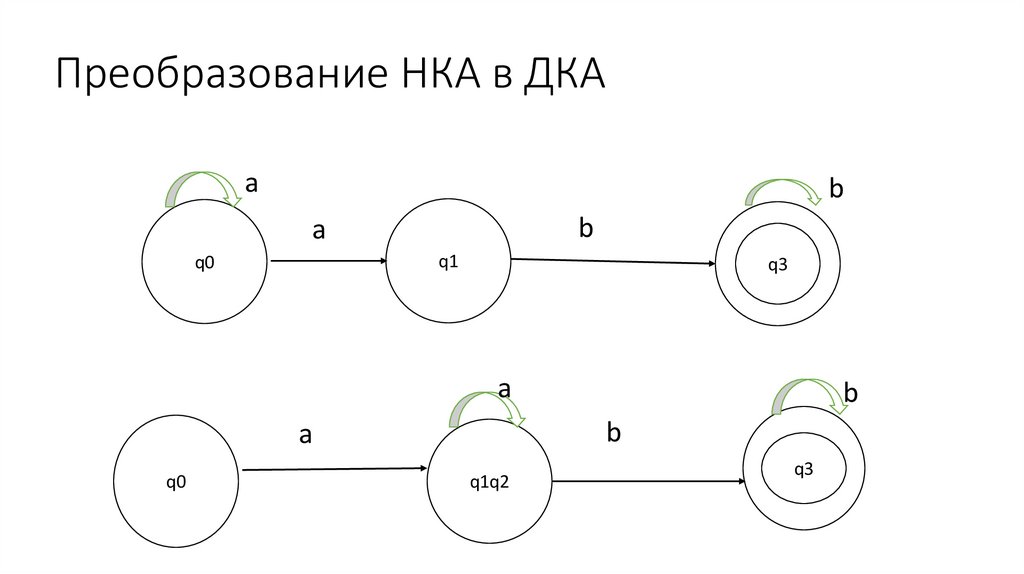
Преобразование НКА в ДКА
a
b
b
a
q1
q0
q3
a
b
a
q0
b
q1q2
q3

5.

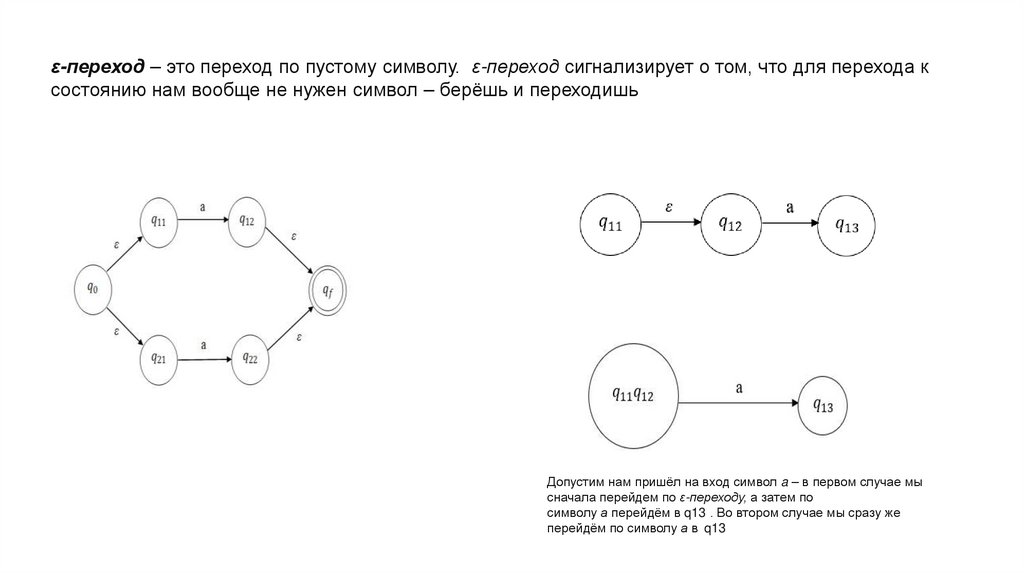
ε-переход – это переход по пустому символу. ε-переход сигнализирует о том, что для перехода к
состоянию нам вообще не нужен символ – берёшь и переходишь
Допустим нам пришёл на вход символ a – в первом случае мы
сначала перейдем по ε-переходу, а затем по
символу а перейдём в q13 . Во втором случае мы сразу же
перейдём по символу а в q13

6.

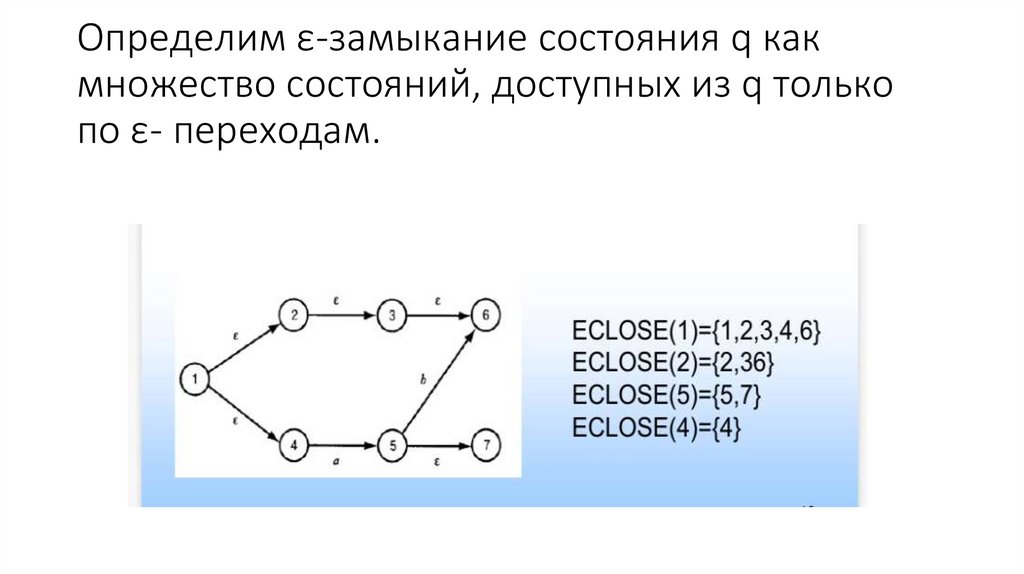
Определим ε-замыкание состояния q как
множество состояний, доступных из q только
по ε- переходам.

7.

Алгоритм Томпсона
• Как сделать из НКА ДКА?
• Убрать одноимённые переходы и избавиться от ε-переходов.
• В алгоритме Томпсона если рассматривать КА как граф, то это классический BFS (обход в
ширину), с схлопыванием ε-переходов и объединением состояний, в которые ведут
одноимённые переходы.
• Шаг 1. Помещаем в очередь Queue множество, состоящее только из стартовой вершины.
Шаг 2. Затем, пока очередь не пуста выполняем следующие действия:
• Достаем из очереди множество, назовем его q
• Для всех c ∈ Σ посмотрим в какое состояние ведет переход по символу c из каждого
состояния в q.
• Полученное множество состояний положим в очередь Queue только если оно не лежало
там раньше.
• Каждое такое множество в итоговом ДКА будет отдельной вершиной, в которую будут
вести переходы по соответствующим символам.

8.

• 3. Определить, какие множества допускают следующие
недетерминированные конечные автоматы (НКА) (предварительно
построить для НКА диаграммы Мура):
• 1) Q = {q1, q2}, f(0, q1) = {q1, q2}, f(1, q1) = {q2}, f(0, q2) = {q2}, f(1, q2) =
{q1, q2}, F = {q2}.
• 2) Q = {q1, q2}, f(0, q1) = {q1, q2}, f(1, q1) = {q2}, f(0, q2) = {q2}, f(1, q2) =
{q1, q2}, F = {q1}.
• 3) Q = {q1, q2, q3}, f(0, q1) = {q2}, f(1, q1) = {q1, q2}, f(0, q2) = {q3}, f(1, q2)
= {q3}, f(0, q3) = {q3}, f(1, q3) = {q2, q3}, F = {q3}.
• 4) Q = {q1, q2, q3}, f(0, q1) = {q1, q2}, f(1, q1) = {q1}, f(0, q2) = {q2}, f(1, q2)
= {q2, q3}, f(0, q3) = {q1, q3}, f(1, q3) = {q1, q3}, F = {q3}.

9.

Операция
ε-closure(q)
Описание
Множество состояний, достижимых из
состояния q ТОЛЬКО по ε-переходам
ε-closure(Q)
Множество состояний, достижимых из
КАКОГО-ЛИБО состояния q ∈ Q ТОЛЬКО
по ε-переходам
move(Q, a)
Множество состояний НКА, в которые
мы можем перейти из q ∈ Q по
символу а

10.

11.

12.

• Q′= ∅
• δ′ = ∅
• Queue = ∅
• currStates = ∅ // Мн-во состояний из очереди
• newStates = ∅ // Мн-во состояний, в которые можно попасть из currStates
• Queue = Queue ∪ q0
• while (Queue ∉ ∅)
currStates = Queue.pop()
• currStates = currStates ∪ ε-closure(currStates)
• foreach (a ∈ Σ)
newStates = move (currStates, a)
if (ε-closure(newStates) ∉ Q′)
Queue = Queue ∪ newStates
Q′ = Q′ ∪ ε-closure(newStates)
end
if (newStates ∉ ∅)
δ′ = δ′ ∪ δ(currStates, a)
end
• end foreach
• end while

13.

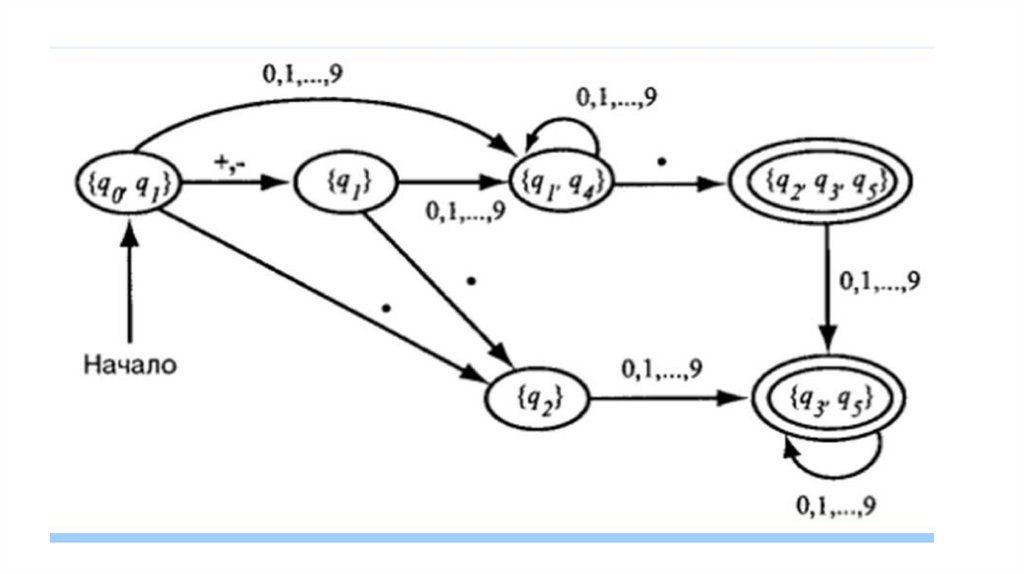
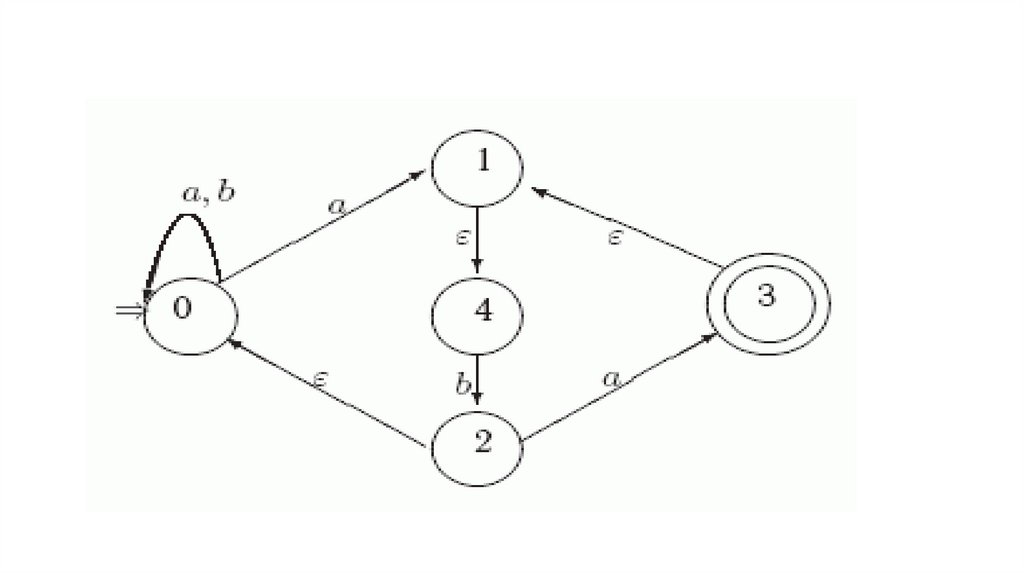
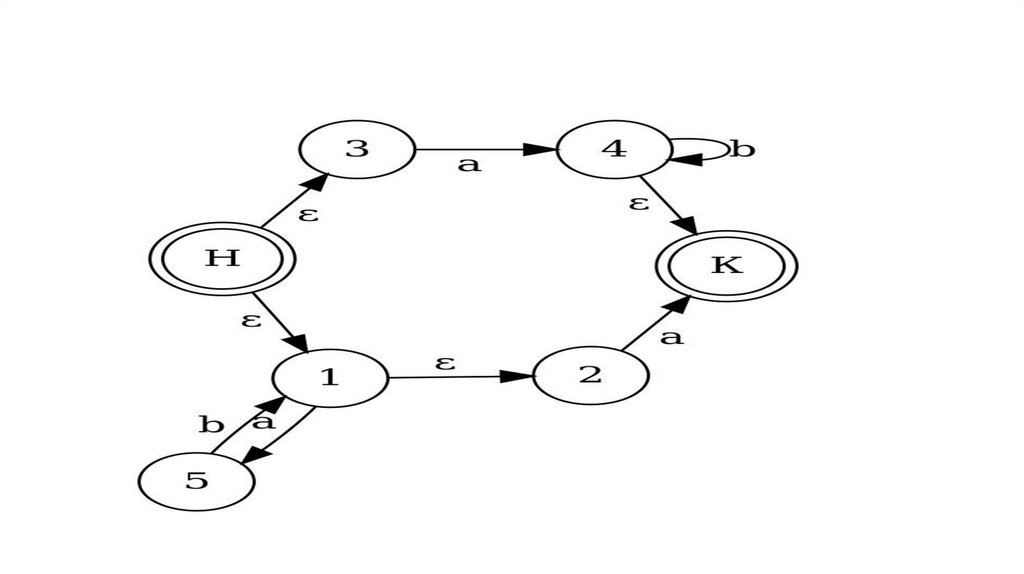
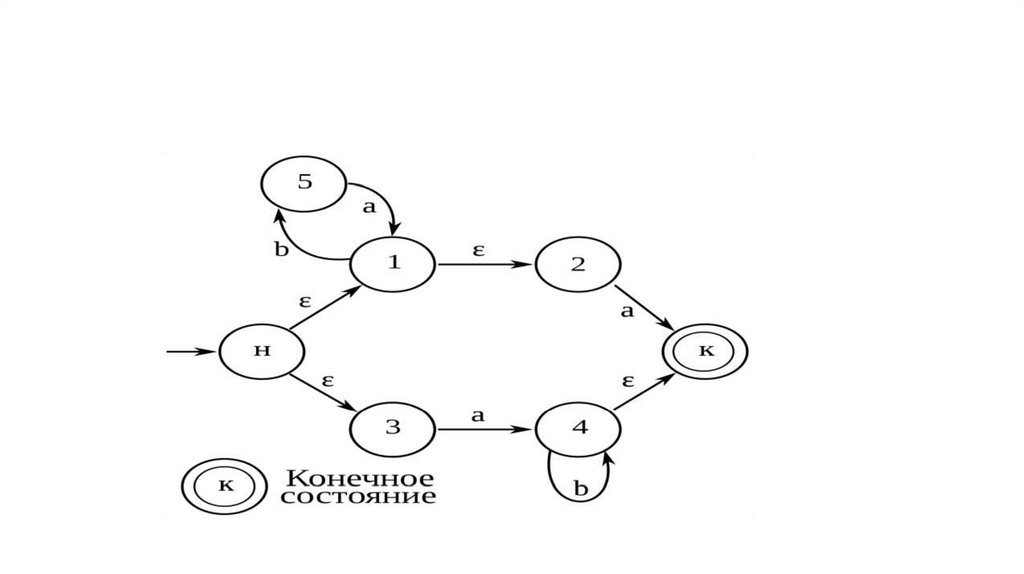
14.

15.

16.

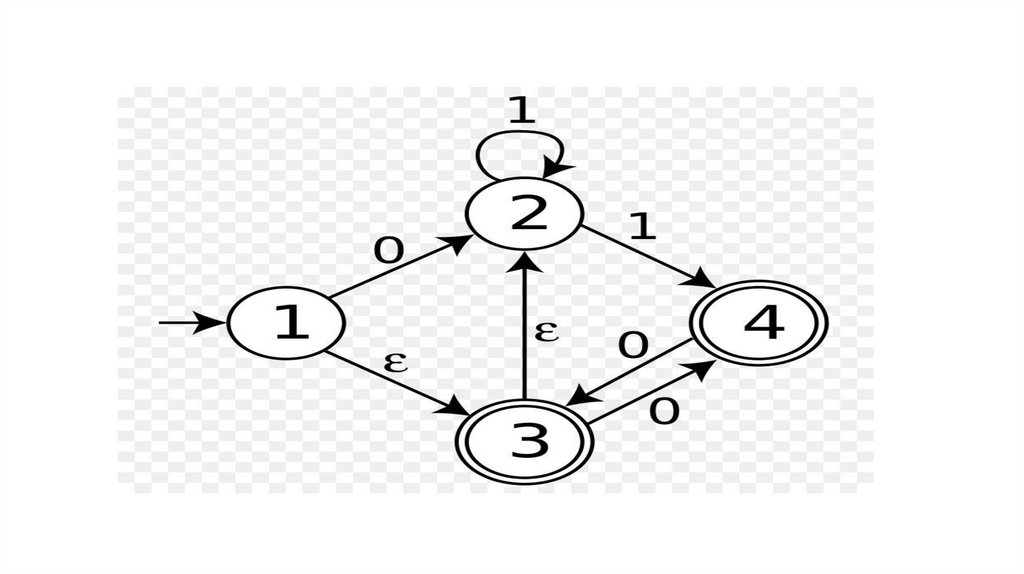
17.

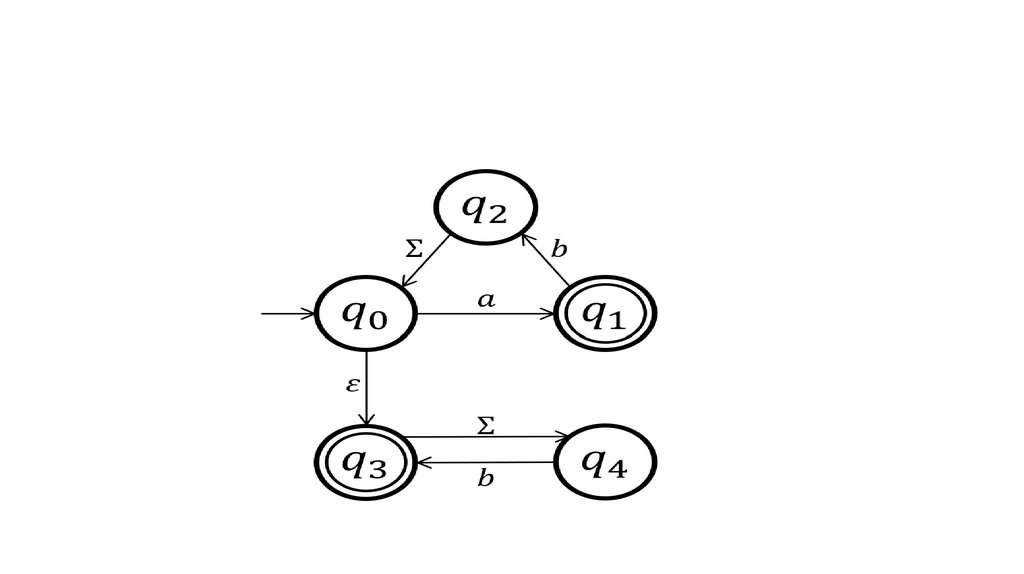
18.

19.

• Алгоритм преобразования НКА в эквивалентный ДКА / Хабр
(habr.com)