Похожие презентации:
Методы многомерного анализа в психологии
1. Методы многомерного анализа в психологии
2.
Максимальноеколичество
баллов
Вид работы
Экзаменационная письменная работа
40
Работа на практических занятиях (6 занятий по
6 баллов)
6х6=36
Практические письменные работы (3 работы по
8 баллов)
3х8=24
Бонусные баллы за работу на лекциях
До 4
баллов
Итог 100+ бонус
3. Лекция 1. Введение в многомерный статистический анализ
4.
1. Общее представление о многомерном анализеданных
2. Выборка и шкалы измерений
3. Числовые характеристики распределений.
Визуальный анализ данных
4. Краткий обзор методов многомерного анализа
статистических данных
http://statosphere.ru/books-arch/statisticabooks/85-halafyan.html
http://www.statcats.ru/2016/03/blog-post.html
http://statistica.ru/textbook/elementarnyeponyatiya-statistiki/#23
5.
Г. Галилей: «Измеряй все, поддающеесяизмерению, и сделай таким все, не
поддающееся измерению»
1890 – из послесловия
Ф.Гальтона к книге
Джеймса Кеттела (Cattell
J.) Mental Test and
Measurements:
«Психология не может
стать прочной и точной,
как физические науки,
если не будет
основываться на
эксперименте и
измерении»
6.
Измерение в психологии:диагностические процедуры, направленные на
определение количественной выраженности тех
или иных психологических феноменов;
используются шкалы, представляющие собой
некоторое множество символов, прежде всего
математических, которые ставятся в определенное
соответствие с психологическими элементами
7.
Многомерным статистическим анализом называетсяраздел математической статистики, изучающий
методы сбора и обработки многомерных
статистических данных, их систематизации и
обработки с целью выявления характера и структуры
взаимосвязей между компонентами исследуемого
многомерного признака, получения практических
выводов
Калинина, Введение в многомерный статистический
анализ
8.
Многомерный статистический анализ дает возможность получитьобщие выводы относительно всей совокупности данных.
Учитывая, что анализируемые данные являются стохастическими,
т.е. ограниченными и неполными, использование методов
многомерного анализа является не только оправданным, но и
существенно необходимым.
Халафян, Учебник STATISTICA 6. Статистический анализ данных
9.
http://statosphere.ru/books-arch/statistica-books/85halafyan.htmlМногомерный статистический анализ раздел математической статистики, посвященный
математическим методам построения оптимальных
планов сбора, систематизации и обработки
многомерных статистических данных, направленных
на выявление характера и структуры взаимосвязей
между компонентами исследуемого многомерного
признака и предназначенных для получения научных
и практических выводов.
10.
Под многомерным признаком понимается р-мерный вектор X =(х1,х2 …, хр) показателей (признаков, переменных) х1, x2...,хр,
среди которых могут быть количественные, т.е. скалярно
измеряющие в определенной шкале степень проявления
изучаемого свойства объекта; порядковые (или ординальные),
т.е. позволяющие упорядочить анализируемые объекты по
степени проявления в них изучаемого свойства; и
классификационные (или номинальные), т.е. позволяющие
разбивать исследуемую совокупность объектов на однородные
(по анализируемым свойствам) классы.
11.
Стивенс, 1946, 1951: измерение как «приписывание чиселобъектам или событиям согласно правилам»
4 шкалы измерений:
Наименований (один объект отличается от другого)
Порядковая (один объект в чем-то превосходит другой)
Интервальная (один объект на сколько-то больше другого)
Отношений (один объект в какое-то количество раз отличается
от другого, есть нулевая точка – «абсолютный ноль»)
Интервальные измерения: истинная разность последовательных
единиц шкалы равна разности двух любых последовательных
целых единиц этой шкалы.
Какой тип шкалы?
Школьные оценки
Шкала Цельсия
Шкала Лайкерта (Ликерта)
Шкала Терстоуна (шкала равнокажущихся интервалов)
12.
По материалам Википедии от 08.02.2017Шкала Лайкерта, или Ликерта (Likert scale /'lɪkərt/, шкала суммарных оценок) испытуемый оценивает степень своего согласия с каждым суждением, от
«полностью согласен» до «полностью не согласен». Сумма оценок
отдельных сужений позволяет выявить установку испытуемого по какомулибо вопросу. Предполагается, что отношение к исследуемому предмету
основано на простых непротиворечивых суждениях и представляет
собой континуум от одной критической точки через нейтральную к
противоположной критической.
«Шкала Лайкерта» может означать два разных понятия:
(1) суммативный психометрический конструкт, то есть свойство,
измеряемое суммой баллов от всех пунктов, относимых к этому свойству; (2)
балльная оценочная (рейтинговая) шкала для каждого отдельного пункта.
Рейтинговые шкалы типа лайкертовских (2) более корректно считать
порядковыми, а не интервальными по уровню измерения, однако на
практике их часто принимают за интервальные, так как методов обработки
интервальных данных больше и они проще. Суммативная шкала
Лайкерта — поскольку она суммирует баллы — трактует рейтинговую шкалу
пунктов как интервальную (порядковые данные суммировать невозможно)
13.
Генеральная совокупность – это любая совокупность объектов,относительно которой исследователь делает вывод. Теоретически
генеральная совокупность неограниченна.
Выборка – любая подгруппа элементов (испытуемых,
респондентов) выделенная из генеральной совокупности для
проведения эксперимента. Оптимально, если каждый участник
генеральной совокупности имеет равную вероятность быть
включенным в исследование
Выборочное исследование – исследование, при котором
производится выбор ограниченного числа элементов из изучаемой
генеральной совокупности.
14.
Требования к выборке:1. Однородность. Выбор осуществляется на основаниях:
возраст, уровень интеллекта, национальность, заболевания.
2. Репрезентативность. Качество выборки, позволяющее
распространять полученные на ней выводы на всю генеральную
совокупность. Состав экспериментальной выборки - это модель
генеральной совокупности.
Любая выборка может быть репрезентативной лишь в какихто определенных, но не всех отношениях. Например, если
выборка сделана по социально-образовательному признаку, это
не значит, что она будет репрезентативна и для возрастной
структуры населения или для разных типов семьи и т.д.
Рекомендуемый объем выборки: не менее 30-35 человек в
изучаемой группе.
При использовании методов многомерного анализа объем
выборки должен быть существенно больше: от 100-150
испытуемых.
15.
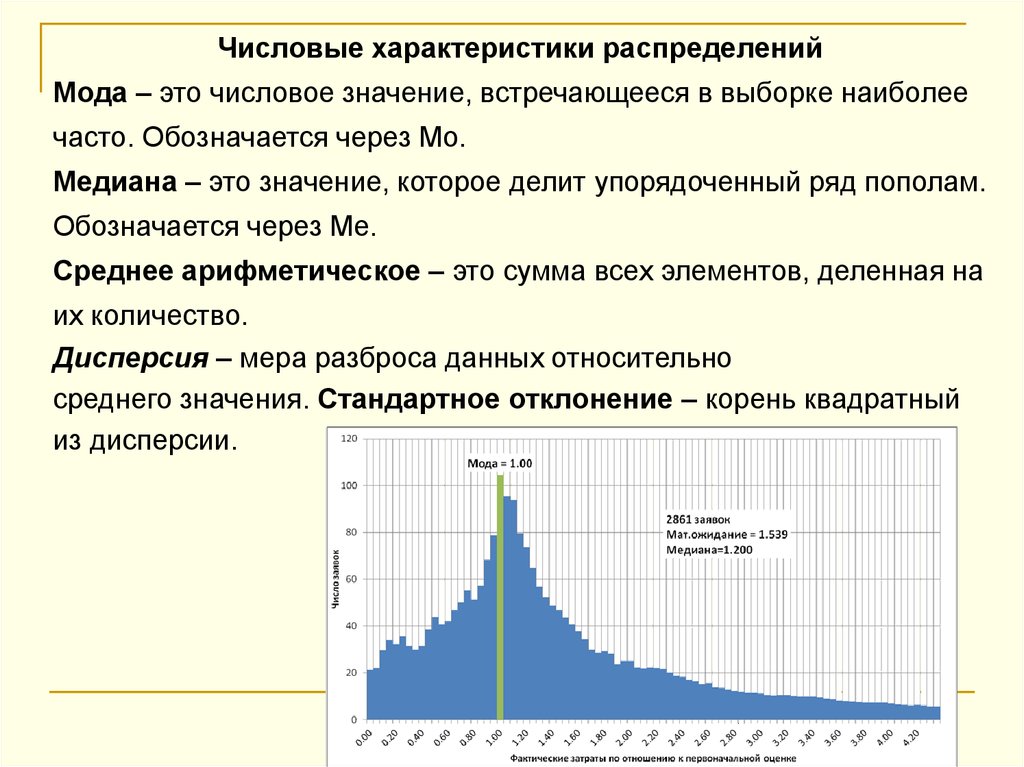
Числовые характеристики распределенийМода – это числовое значение, встречающееся в выборке наиболее
часто. Обозначается через Мo.
Медиана – это значение, которое делит упорядоченный ряд пополам.
Обозначается через Ме.
Среднее арифметическое – это сумма всех элементов, деленная на
их количество.
Дисперсия – мера разброса данных относительно
среднего значения. Стандартное отклонение – корень квадратный
из дисперсии.
16.
http://www.statcats.ru/2016/03/blog-post.htmlВладимир Савельев: Статистика и котики
17.
18.
19.
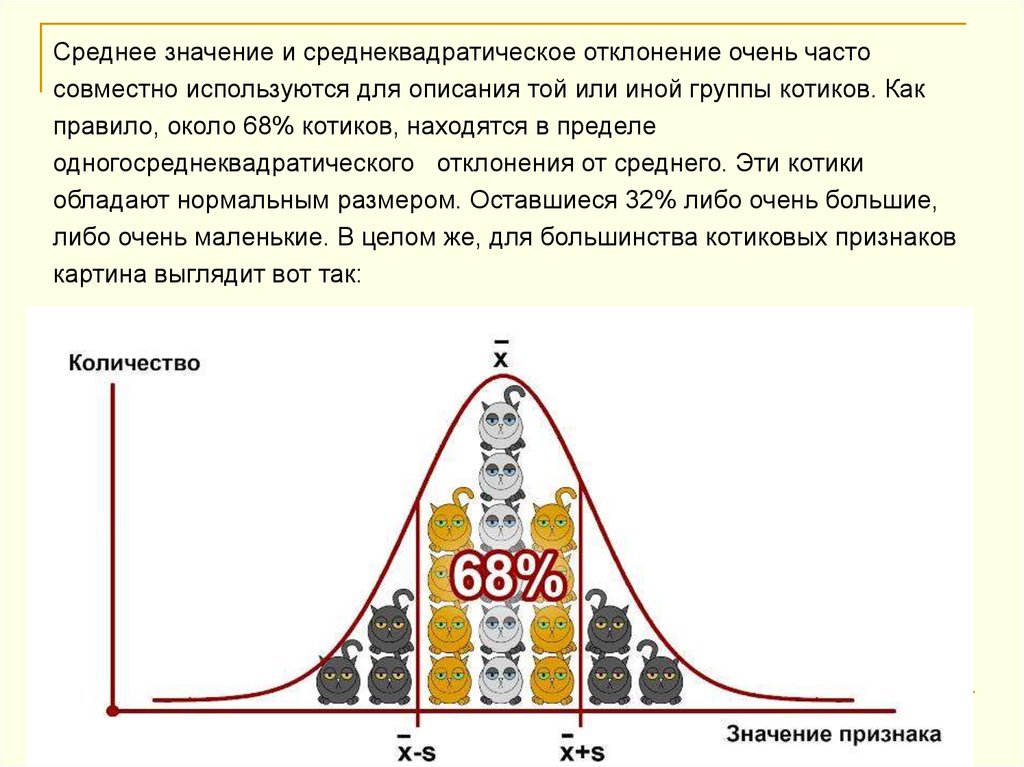
Среднее значение и среднеквадратическое отклонение очень частосовместно используются для описания той или иной группы котиков. Как
правило, около 68% котиков, находятся в пределе
одногосреднеквадратического отклонения от среднего. Эти котики
обладают нормальным размером. Оставшиеся 32% либо очень большие,
либо очень маленькие. В целом же, для большинства котиковых признаков
картина выглядит вот так:
20.
Нормальное распределениеНормальное распределение вероятностей особенно часто
используется в статистике.
Нормальное распределение дает хорошую модель для реальных
явлений, в которых:
1) имеется сильная тенденция данных группироваться вокруг
центра;
2) положительные и отрицательные отклонения от центра
равновероятны;
3) частота отклонений быстро падает, когда отклонения от центра
становятся большими.
Механизм, лежащий в основе нормального распределения,
объясняется с помощью
центральной предельной теоремы:
21.
Центральная предельная теоремаОсновная идея: при суммировании большого числа
независимых величин в определенных разумных условиях
получаются именно нормально распределенные величины.
Иными словами, если на некоторую переменную воздействует
множество факторов, эти воздействия независимы,
относительно малы и слагаются друг с другом, то получаемая в
итоге величина имеет нормальное распределение.
Визуально график нормальной плотности - знаменитая
колоколообразная кривая.
Нормальное распределение описывается двумя параметрами:
mean — среднее;
stantard deviation — стандартное отклонение
22.
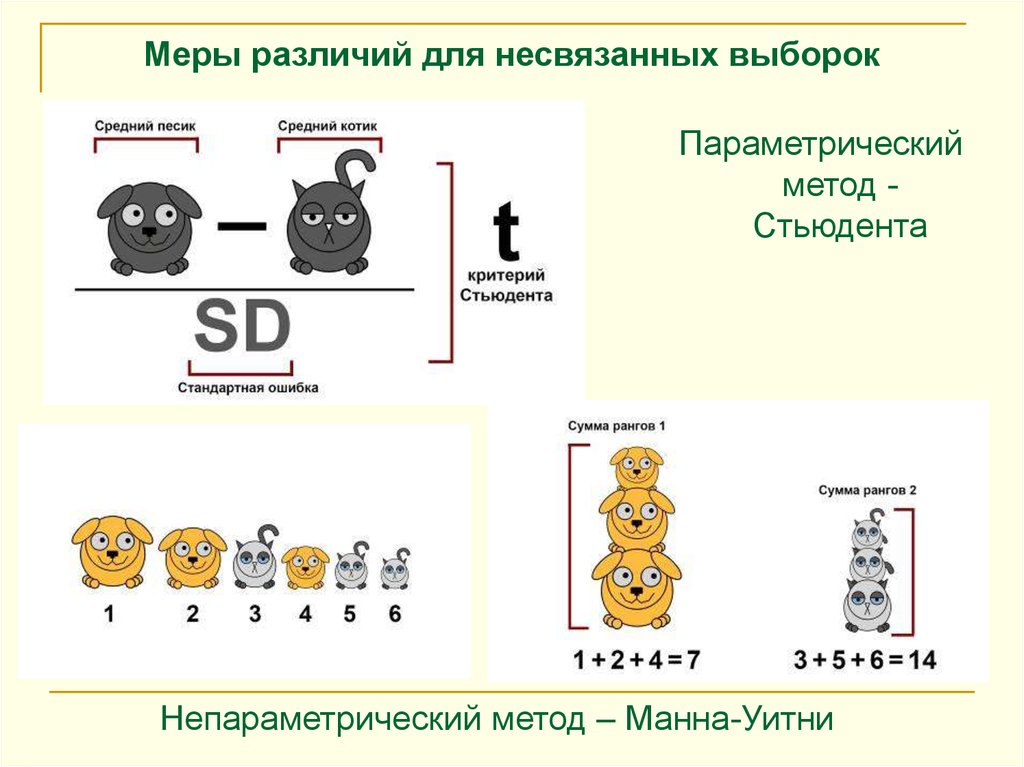
Меры различий для несвязанных выборокПараметрический
метод Стьюдента
Непараметрический метод – Манна-Уитни
23.
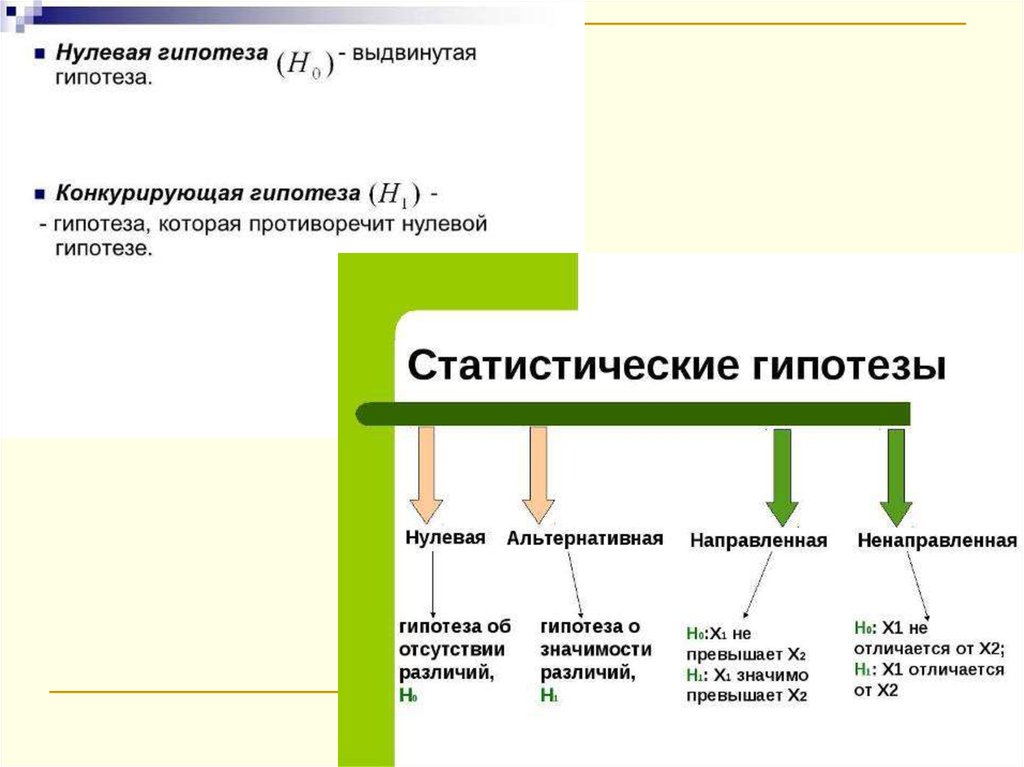
Статистическая гипотеза – научная гипотеза,допускающая статистическую проверку.
Примеры:
Исследование интеллекта у подростков из полных и неполных
семей. Можно ли сделать вывод о том, что неполная семью ведет
к снижению интеллекта у подростков?
Неработающие женщины имеют показатели самооценки ниже, чем
работающие женщины. Можно ли утверждать, что трудовая
занятость способствует повышению самооценки? Эти решения
всегда вероятностны.
Выделяют нулевую и альтернативную гипотезы. Пример:
Нулевая гипотеза (H0) – гипотеза об отсутствии связи в
генеральной совокупности.
Альтернативная (H1) – гипотеза о наличии связи.
Уровень значимости – вероятность ошибочного отклонения
нулевой гипотезы.
24.
25.
Двухмерный - 2М визуальный анализВизуальный анализ данных на плоскости. В
двухмерном визуальном анализе используются
разнообразные гистограммы, диаграммы рассеяния,
вероятностные графики, линейные графики,
диаграммы диапазонов, размахов, круговые
диаграммы, столбчатые диаграммы,
последовательные графики (графики
последовательных значений) и т. д., позволяющие
увидеть специфику данных.
26.
Термин гистограмма ввел Карл Пирсон в 1895 году.Гистограммы позволяют увидеть, как распределены
значения переменных по интервалам группировки, то
есть как часто переменные принимают значения из
различных интервалов.
Наглядно показывают, какие значения или
диапазоны значений исследуемой переменной
являются наиболее частыми, насколько сильно они
различаются между собой, как сконцентрировано
большинство наблюдений вокруг среднего, является
распределение симметричным или нет, имеет ли оно
одну моду или несколько мод, то есть является
мультимодальным.
27.
Histogram (ЭкПс-2015-17-за два года-стандарт.sta 88v*188c)идентиф_прир_nrs = 188*0,5*normal(x; -4,2934E-17; 1)
экол_экстрапол_nrs = 188*0,5*normal(x; 1,5266E-16; 1)
эмоц_оп_взаим_пр = 188*0,5*normal(x; -3,4191E-15; 1)
60
50
No of obs
40
30
20
10
0
-4,0
-3,0
-3,5
-2,0
-2,5
-1,0
-1,5
0,0
-0,5
1,0
0,5
2,0
1,5
3,0
2,5
идентиф_прир_nrs
экол_экстрапол_nrs
эмоц_оп_взаим_пр
Гистограмма, или распределение частот
значений переменной по интервалам,
представляет интерес по следующим
причинам:
по форме распределения можно
охарактеризовать природу исследуемой
переменной (например, наличие двух мод наиболее высоких столбцов гистограммы,
иначе говоря - бимодальность распределения
может означать, что выборка неоднородна и
состоит из наблюдений, принадлежащих двум
различным генеральным совокупностям);
многие статистики критериев основаны на
определенных предположениях о виде
распределения, например, на предположении
нормальности; гистограммы помогают
визуально проверить выполнение этих
предположений.
28.
Краткий обзорметодов многомерного анализа данных
29.
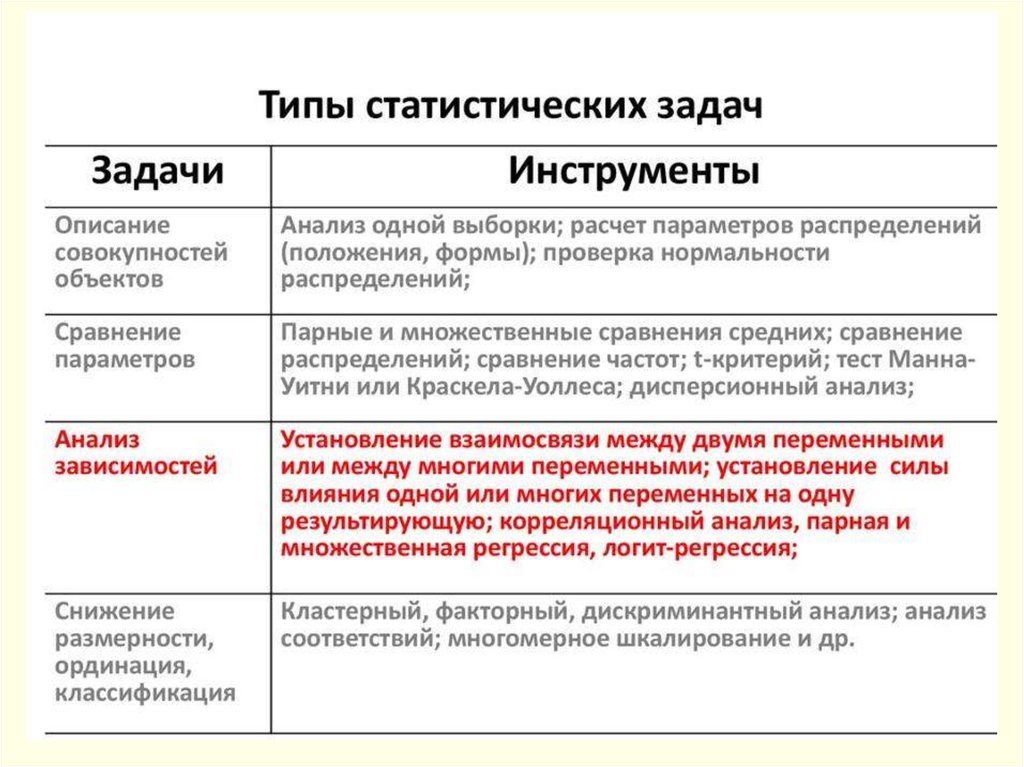
Корреляционный анализ. Корреляционныеплеяды, корреляционные графы.
Корреляция –согласованное изменение признаков. Если при
изменении одной величины изменяется другая, то между их
показателями будет наблюдаться корреляция. Наличие
корреляции двух переменных не говорит о причинноследственных зависимостях между ними, однако дает
возможность выдвинуть такую гипотезу.
Регрессионный анализ - количественное
представление связи или зависимости между X и Y.
Множественная регрессия (предикторы, зависимая
переменная)
Дисперсионный анализ (анализ изменчивости признака
под влиянием каких-либо контролируемых переменных факторов)
Кластерный анализ (группировка данных)
Факторный анализ (метод сокращения данных)
























 Психология
Психология








