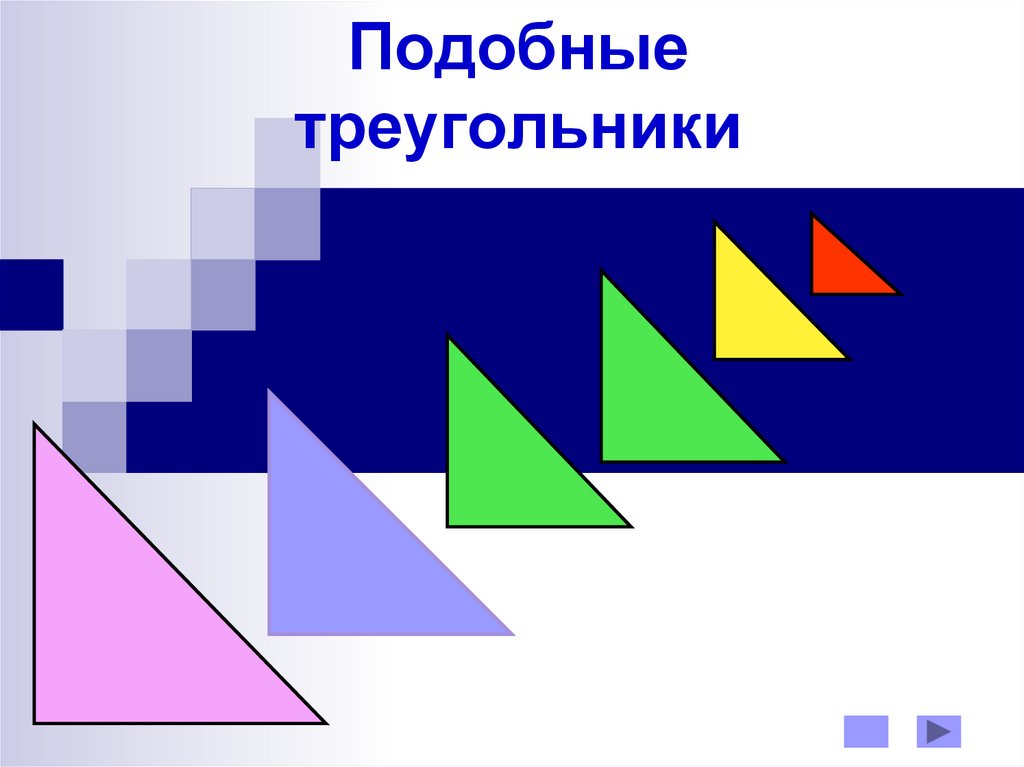
Подобные треугольники

1.

Подобные
треугольники

2.

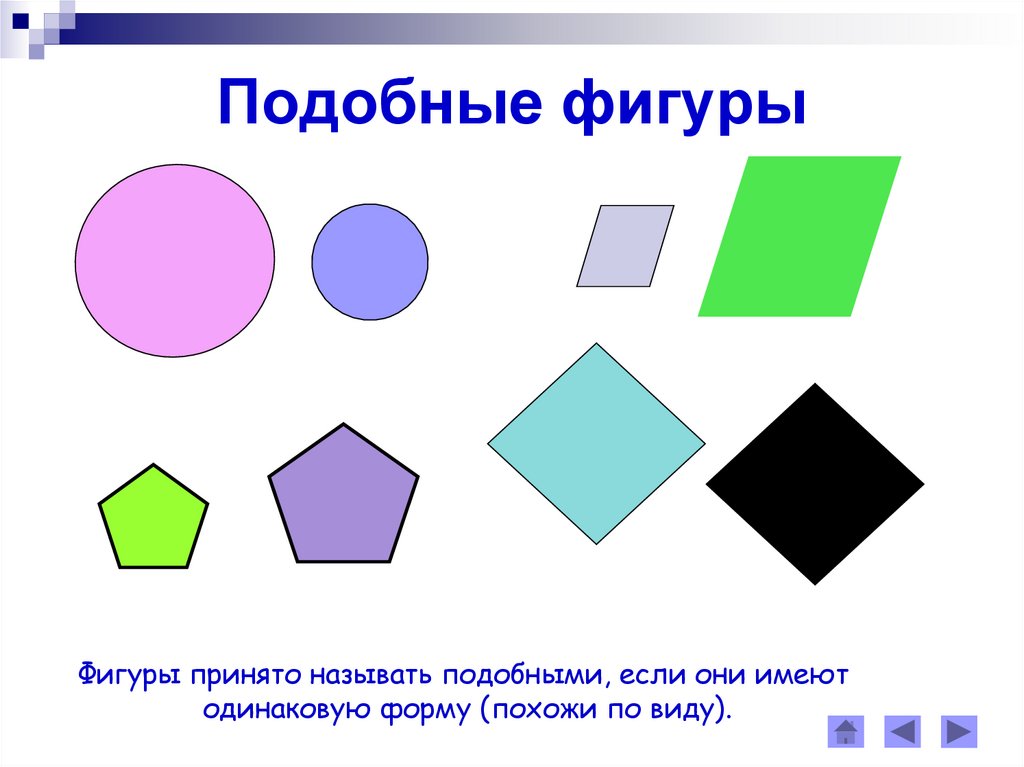
Подобные фигуры
Фигуры принято называть подобными, если они имеют
одинаковую форму (похожи по виду).

3.

Подобие в жизни(карты местности)

4.

Пропорциональные отрезки
Определение: отрезки называются пропорциональными,
если пропорциональны их длины.
12 см
А1
С1
8 см
12
6
В1
К1
А
С
8
4
А 1В 1
АВ
6 см
4 см
В
К
С1К1
СК
Говорят, что отрезки А1В1 и С1К1 пропорциональны отрезкам АВ и СК.
Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если:
а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см ?
да
б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см ?
нет
в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см ?
нет

5.

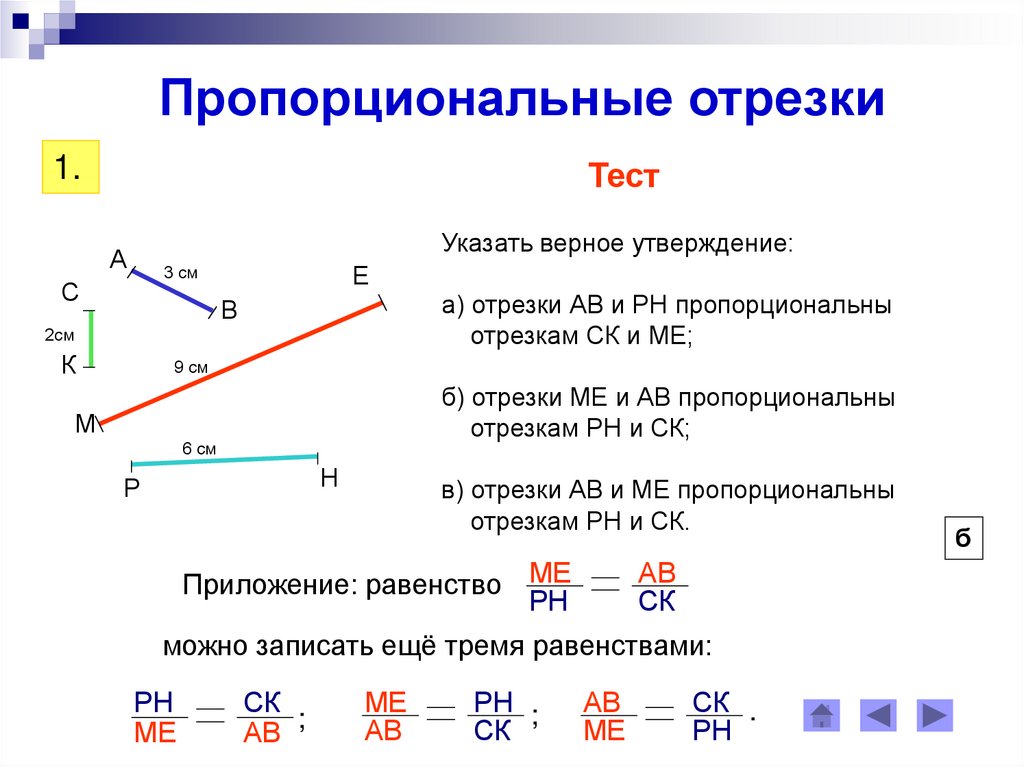
Пропорциональные отрезки
1.
Тест
Указать верное утверждение:
А
Е
3 см
С
а) отрезки АВ и РН пропорциональны
отрезкам СК и МЕ;
В
2см
К
9 см
б) отрезки МЕ и АВ пропорциональны
отрезкам РН и СК;
М
6 см
Н
Р
в) отрезки АВ и МЕ пропорциональны
отрезкам РН и СК.
Приложение: равенство МЕ
РН
АВ
СК
можно записать ещё тремя равенствами:
РН
МЕ
СК
;
АВ
МЕ
АВ
РН ;
СК
АВ
МЕ
СК .
РН
б

6.

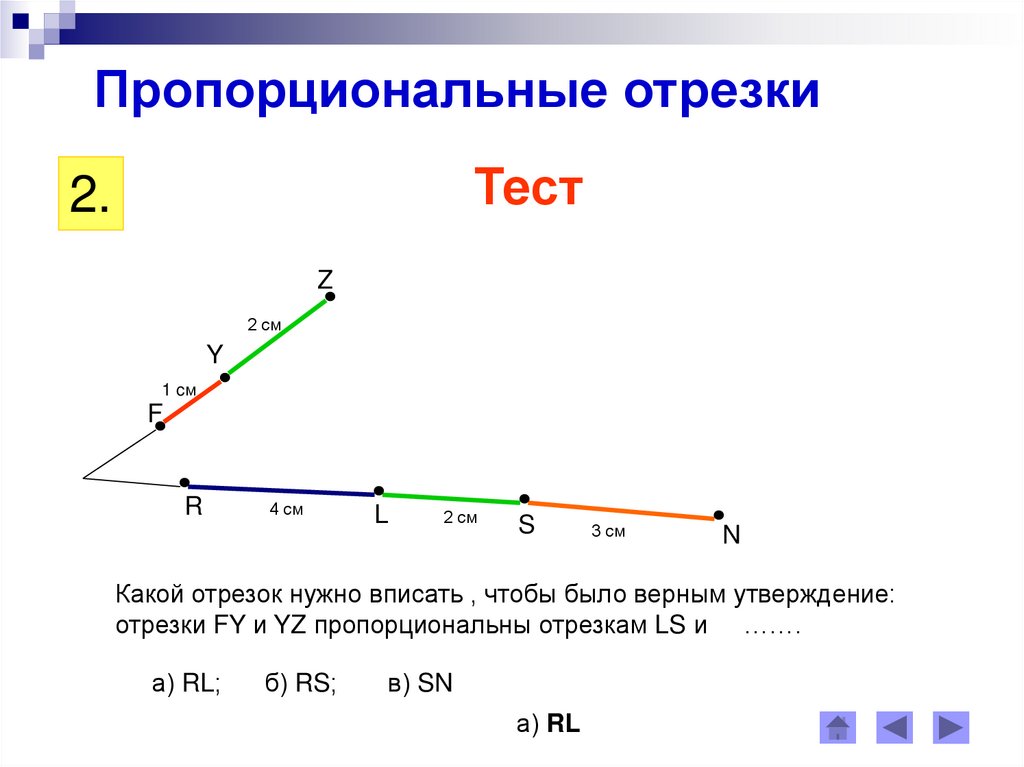
Пропорциональные отрезки
Тест
2.
Z
2 см
Y
1 cм
F
R
4 см
L
2 см
S
3 см
N
Какой отрезок нужно вписать , чтобы было верным утверждение:
отрезки FY и YZ пропорциональны отрезкам LS и …….
а) RL;
б) RS;
в) SN
а) RL

7.

Пропорциональные отрезки
(свойство)
Биссектриса треугольника делит противоположную сторону
на отрезки, пропорциональные прилежащим
сторонам треугольника.
Дано:
А
АВС, АК – биссектриса.
Доказать:
12
ВК
АВ
КС
АС
Доказательство:
Н
В
К
С
Т. к. АК – биссектриса, то 1 =
2, значит,
АВК и АСК имеют по равному углу, поэтому
АВ ∙ АК
SАВК
AB
AC
АС ∙ АК
SАСК
BK
AB
KС
Проведём АН ВС.
АC
ВК
S
АВК и АСК имеют общую высоту АН, значит, АВК
КC
SАСК
КС
Следовательно, ВК
АС
АВ

8.

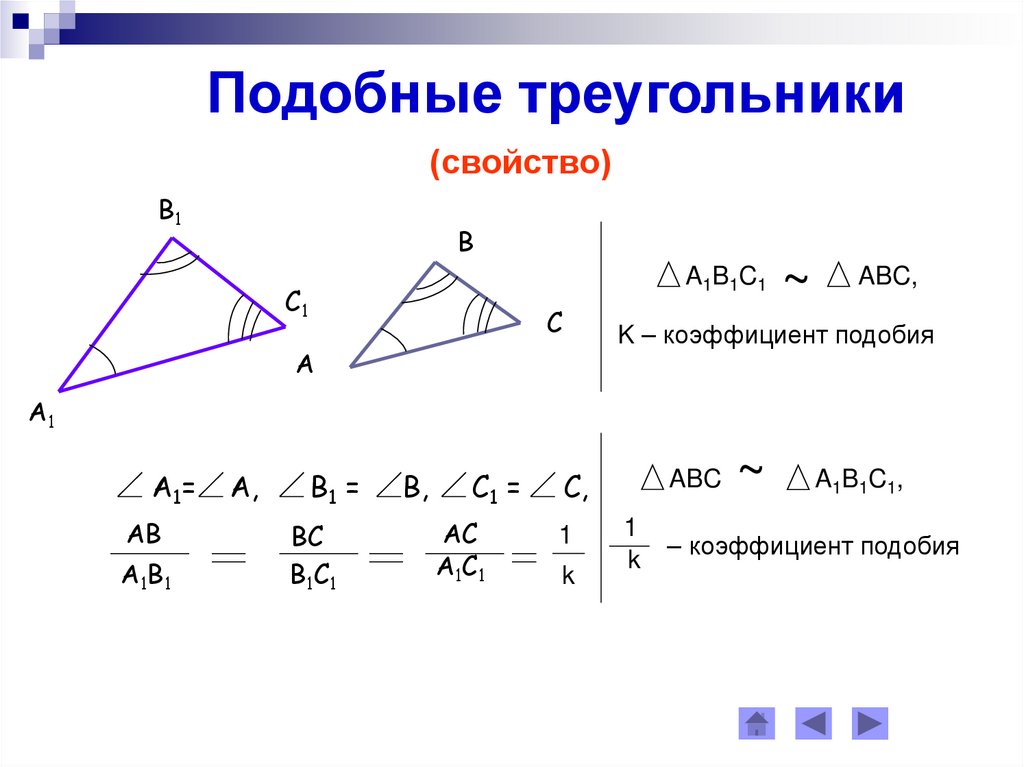
Подобные треугольники
Определение: треугольники называются подобными, если углы
одного треугольника равны углам другого треугольника
и стороны одного треугольника пропорциональны
сходственным сторонам другого.
В1
В
С1
С
А
А1
А1=
А1В1
АВ
А,
В1 =
В1С1
ВС
В,
С1 =
А1С1
АС
С
k
A1B1C1
~
ABC
K – коэффициент подобия
Сходственными сторонами в подобных треугольниках
называются стороны, лежащие против равных углов.

9.

Подобные треугольники
(свойство)
В1
В
A1B1C1
С1
С
~
ABC,
K – коэффициент подобия
А
А1
А 1=
АВ
А1В1
А,
В1 =
ВС
В1С1
В,
С1 =
АС
А1С1
С,
1
k
ABC
1
k
~
A1B1C1,
– коэффициент подобия

10.

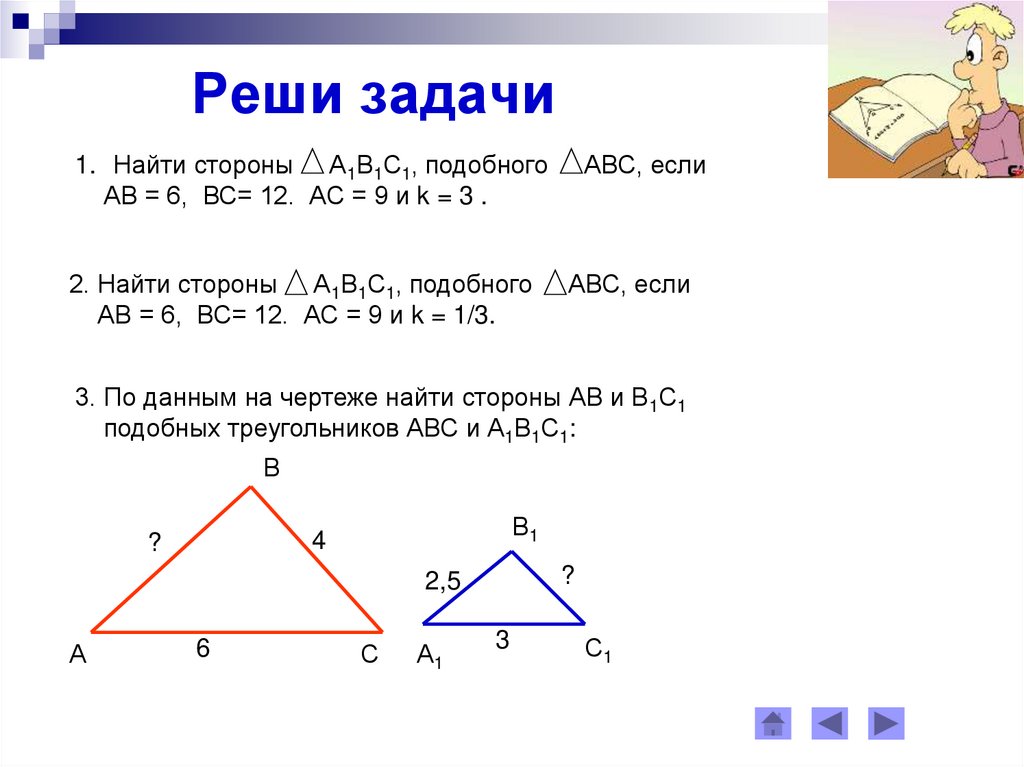
Реши задачи
1. Найти стороны А1В1С1, подобного
АВ = 6, ВС= 12. АС = 9 и k = 3 .
АВС, если
2. Найти стороны А1В1С1, подобного
АВ = 6, ВС= 12. АС = 9 и k = 1/3.
АВС, если
3. По данным на чертеже найти стороны АВ и В1С1
подобных треугольников АВС и А1В1С1:
В
В1
4
?
?
2,5
А
6
С
А1
3
С1

11.

Проверь себя!
1. Верно ли, что у подобных треугольников стороны
соответственно равны?
2. Могут ли быть подобными прямоугольный и
равнобедренный треугольники? Прямоугольный и
тупоугольный треугольники?
3.Могут ли быть подобными треугольник с углом 500 и
треугольник с углом 1000? Треугольник с углом 450 и
треугольник с углом 1350?
4. Треугольники АВС и МNK подобны, причем А = N,
В = K. Назовите сторону, сходственную со стороной MN.