Похожие презентации:
Слайд-лекция «Тройные интегралы»
1. 6B07102 Машиностроение 6B07107 Химическая технология неорганических веществ 6B07305 Инженерные системы и сети 6B11301
Дисциплина: «Математика 2»Слайд-лекция «Тройные интегралы»
6B07102 МАШИНОСТРОЕНИЕ
6B07107 ХИМИЧЕСКАЯ ТЕХНОЛОГИЯ НЕОРГАНИЧЕСКИХ ВЕЩЕСТВ
6B07305 ИНЖЕНЕРНЫЕ СИСТЕМЫ И СЕТИ
6B11301 ОРГАНИЗАЦИЯ ПЕРЕВОЗОК, ДВИЖЕНИЯ И ЭКСПЛУАТАЦИЯ ТРАНСПОРТА
6B07202 МЕТАЛЛУРГИЯ
6B07205 МЕТАЛЛУРГИЯ
6B07110 ТЕХНОЛОГИЧЕСКИЕ МАШИНЫ И ОБОРУДОВАНИЕ (ПО ОТРАСЛЯМ)
6B07103 ТРАНСПОРТ, ТРАНСПОРТНАЯ ТЕХНИКА И ТЕХНОЛОГИИ
6B07302 СТРОИТЕЛЬСТВО
6B07501 СТАНДАРТИЗАЦИЯ, СЕРТИФИКАЦИЯ И МЕТРОЛОГИЯ (ПО ОТРАСЛЯМ)
.
2.
Пусть V – замкнутая и ограниченная область впространстве и в ней определена произвольная
ограниченная функция f(x,y,z).
Разобьем область V на n произвольных частей
V1 , V2 ... Vn
В каждой из областей ΔVi выберем точку
Ai ( xi , yi , zi )
3.
Сумму видаn
f ( xi , yi , zi ) Vi
i 1
называют интегральной суммой
для функции f(x,y,z) в области V.
4.
Еслисуществует
конечный
предел
интегральной суммы при стремлении к 0
наибольшего из фрагментов разбиения, не
зависящий от способа разбиения области
V и выбора точек (xi,yi,zi), то он называется
тройным интегралом от функции f(x,у,z)
по области V.
n
lim
max Vi 0
f ( x , y , z ) V f ( x, y, z)dV
i 1
i
i
i
i
V
5.
Пусть дан тройной интегралI f ( x, y, z )dV
V
dV dxdydz
6.
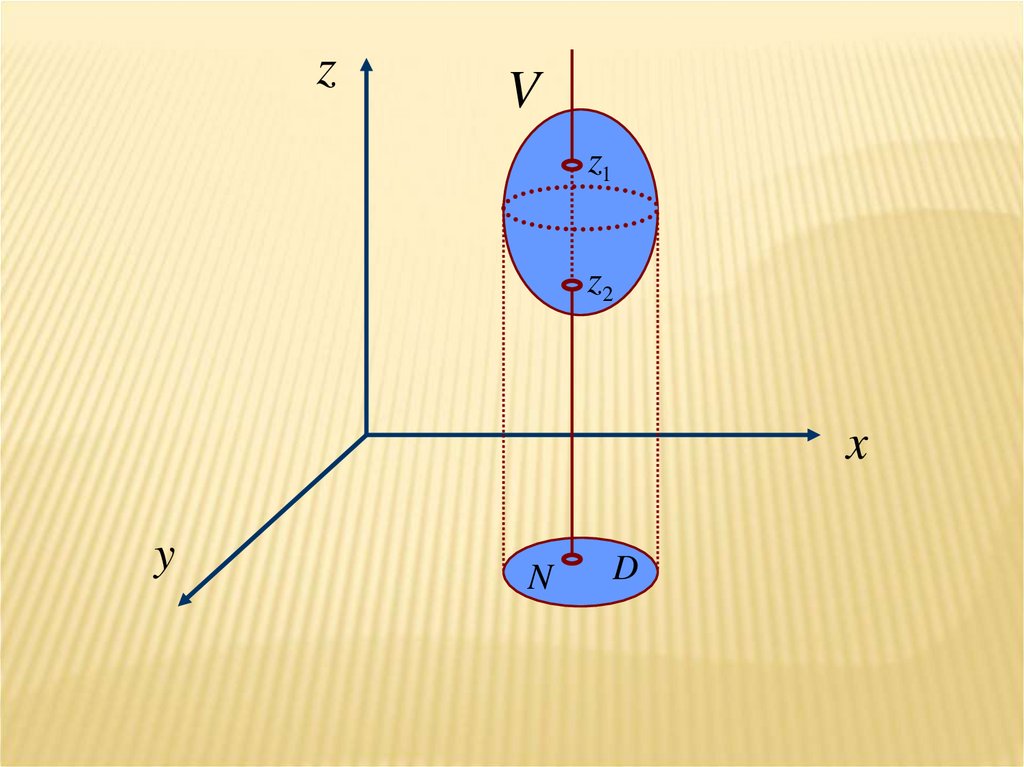
zV
z1
z2
x
y
N
D
7.
1Проектируем поверхность, ограниченную
объемом V, на плоскость ХОУ, получаем
область D.
2
Определяем координаты точек z1 (x,y) и
z2 (x,y) входа и выхода прямой,
параллельной оси z и проведенной
через точку N области D.
8.
3Считая х,у постоянными, вычисляем интеграл:
z2
f ( x , y, z ) dz
z1
А затем двойной интеграл:
z2
dS f ( x , y, z ) dz
D
z1
9.
4Двойной интеграл можно свести к повторному:
b
y2 ( x ) z2 ( x , y )
a
y1 ( x )
I dx dy
f ( x, y, z ) dz
z1 ( x , y )
10.
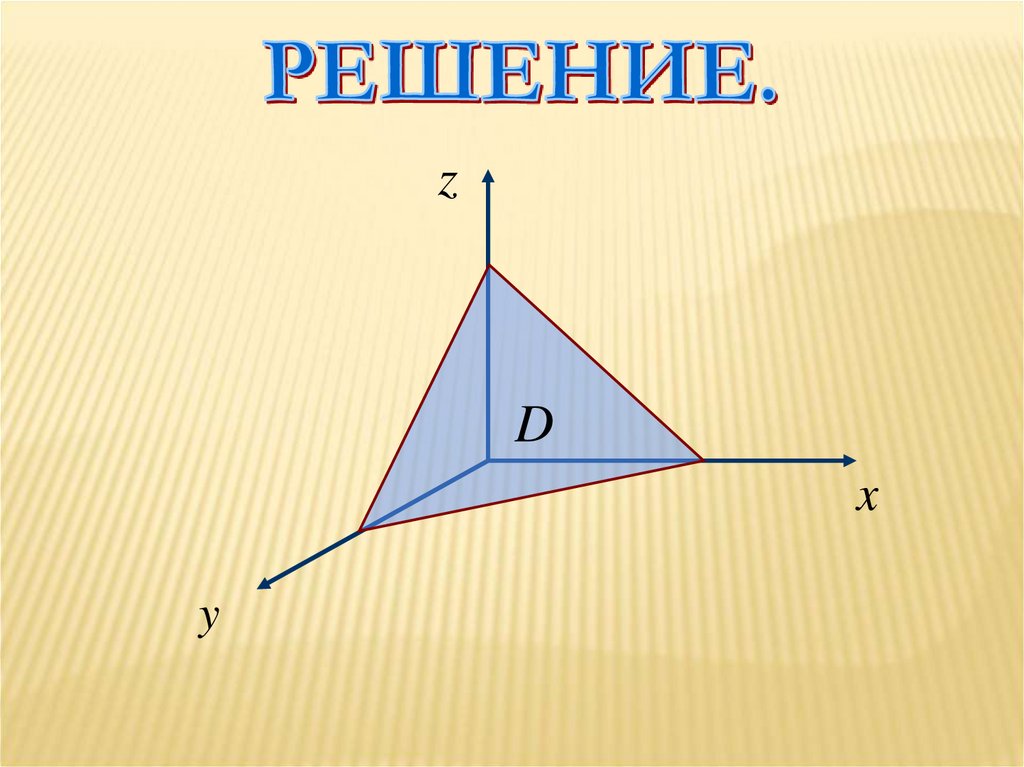
Вычислить тройной интеграл( x y z )dxdydz
V
где V – область, ограниченная
координатными плоскостями
x=0, у=0, z=0 и плоскостью
x+y+z=1
11.
zD
x
y
12.
1По переменной z интегрирование идет от 0 до
z=1-x-y:
1 x y
( x y z)dxdydz dxdy ( x y z)dz
V
D
0
1 x y
z
dxdy ( x y ) z
2 0
D
2
(1 x y) 2
dxdy ( x y) (1 x y)
2
D
13.
2(1 x y)
2
2
dxdy x y x xy xy y
2
D
2
(
1
x
y
)
2
dxdy ( x y) ( x y)
2
D
2
Теперь расставляем пределы интегрирования по
области D: это треугольник со сторонами x=0,
y=0, x+y=1:
14.
1 x2
(
1
x
y
)
2
dx dy ( x y) ( x y)
2
0
0
1
1 x
( x y ) ( x y ) (1 x y )
dx
3
6
2
0
0
1
2
3
3
1 x 2 1 x 3 (1 x)3
dx
6
2 2 3 3
0
1
15.
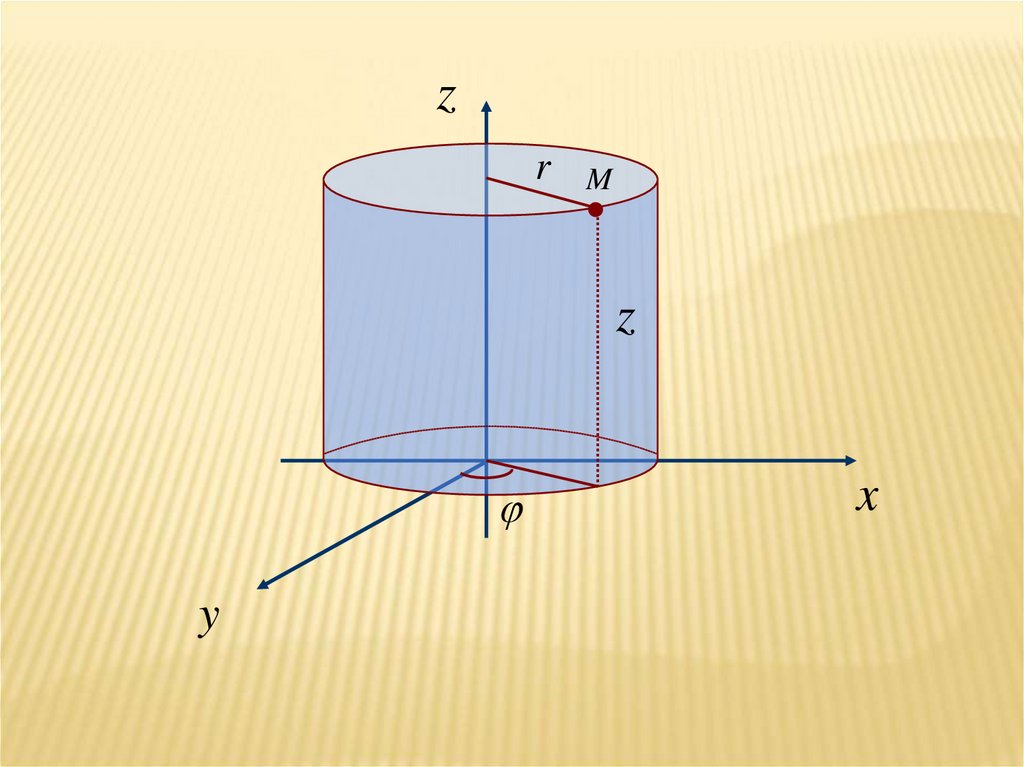
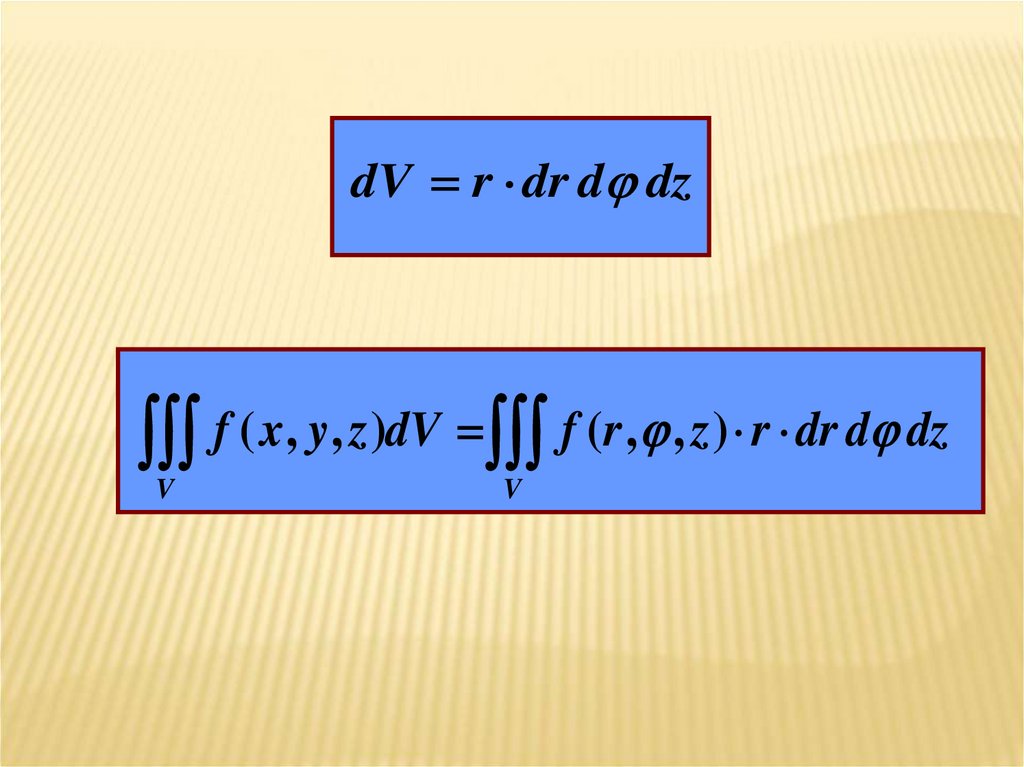
x r cosy r sin
z z
16.
zr
M
z
y
x
17.
dV r dr d dzf ( x, y, z )dV f (r , , z ) r dr d dz
V
V
18.
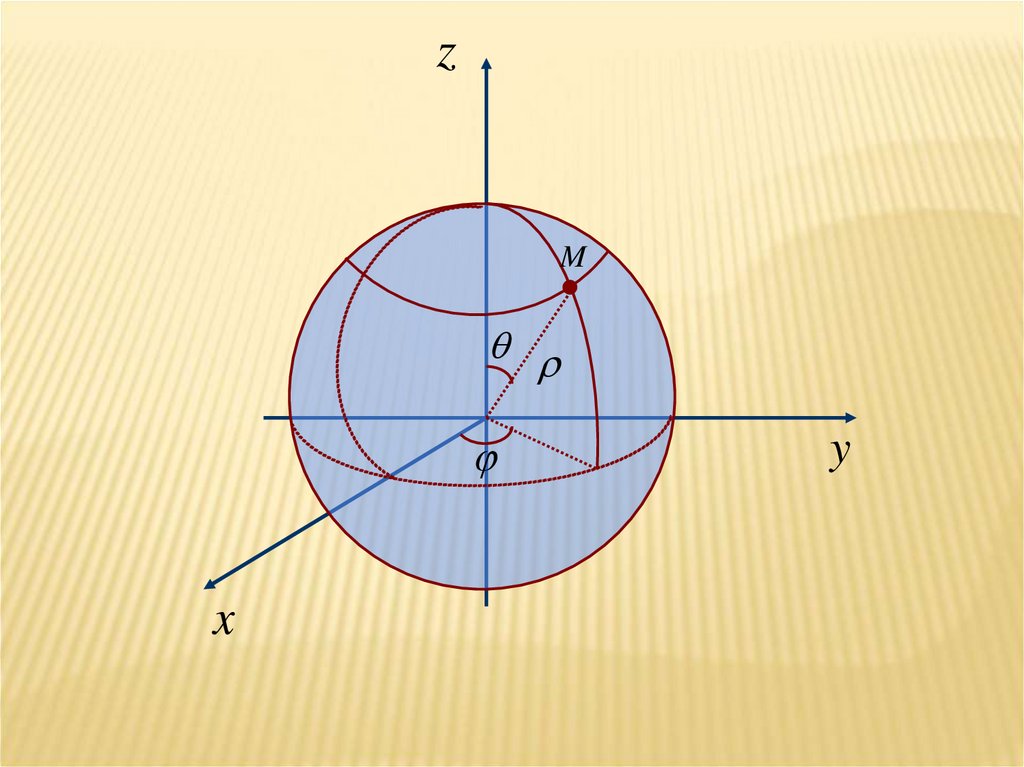
x sin cosy sin sin
z cos
19.
zM
x
y
20.
dV sin d d d2
f ( x, y, z )dV f ( , , ) sin d d d
2
V
V











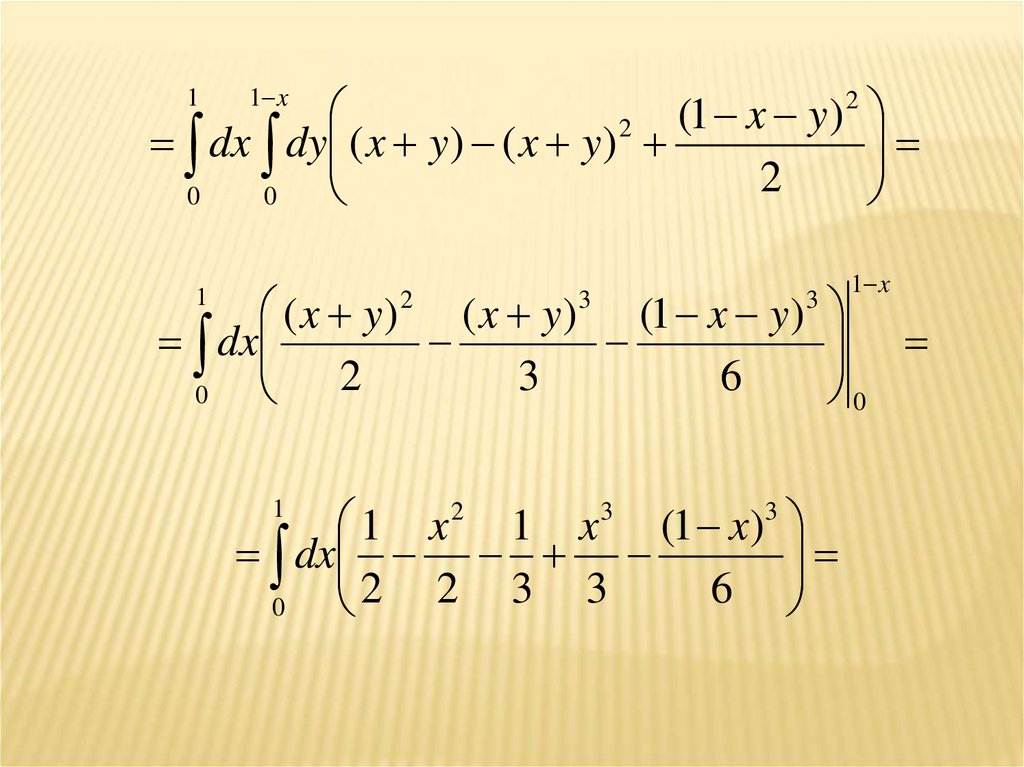



 Математика
Математика








