Тройной интеграл

1. Тройной интеграл

Основные понятия
Вычисления тройного интеграла в декартовых
координатах
1/14

2. Основные понятия

2/14
Основные понятия
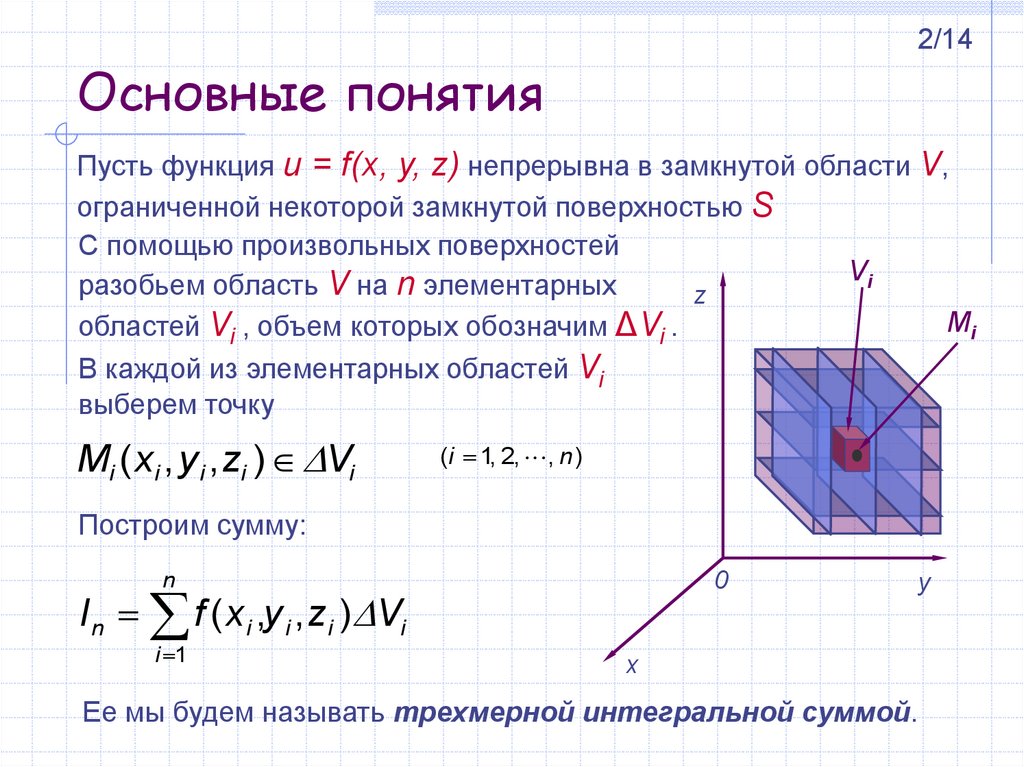
Пусть функция u = f(x, y, z) непрерывна в замкнутой области V,
ограниченной некоторой замкнутой поверхностью S
С помощью произвольных поверхностей
Vi
разобьем область V на n элементарных
z
Mi
областей Vi , объем которых обозначим ΔVi .
В каждой из элементарных областей Vi
выберем точку
Mi ( xi , y i , zi ) Vi
(i 1, 2, , n )
Построим сумму:
0
n
I n f ( x i ,y i , zi ) Vi
i 1
y
x
Ее мы будем называть трехмерной интегральной суммой.

3. Основные понятия

3/14
Основные понятия
Обозначим через d наибольший из диаметров ячеек
(элементарных областей)
Будем неограниченно увеличивать n таким образом, что каждая
элементарная ячейка Vi стягивается в точку.
Предел трехмерной интегральной суммы при d 0 , если этот
предел существует и не зависит от формы ячеек Vi и выбора точек
Мi в них, называется тройным интегралом по области V.
n
f ( x, y, z)dV lim f ( x ,y , z ) V
V
d 0
n i 1
dV = dxdydz – элемент объема
i
i
i
i

4. Основные понятия

4/14
Основные понятия
(существования тройного интеграла)
Теорема
Если функция u = f(x; y; z) непрерывна в замкнутой области V,
то она интегрируема в этой области, то есть предел
трехмерной интегральной суммы при n и d 0
существует и не зависит от способа разбиения области V на
части и от выбора точек Мi в них.
Свойства тройного интеграла
1
c f ( x; y; z)dV c f ( x; y; z)dV
V
2
V
f ( x; y ; z ) f ( x; y ; z ) dV
1
2
v
f ( x; y ; z ) dV f ( x; y ; z ) dV
1
v
2
v

5. Основные понятия

5/14
Основные понятия
3 Если область V разбить на две области V1 и V2 не имеющих
общих точек, то
f ( x; y ; z ) dV f ( x; y ; z ) dV f ( x; y ; z ) dV
v
4
v1
v2
Если в области V имеет место неравенство:
f ( x; y ; z ) 0
f ( x; y; z) dV 0
v
5 Если в области V функции f(x; y; z) и g(x; y; z) удовлетворяют
неравенству:
f ( x; y ; z ) g ( x; y ; z ) f ( x; y; z) dV g( x; y; z) dV
v
v

6. Основные понятия

6/14
Основные понятия
6 Если функция f(x; y; z) непрерывна в замкнутой области,
объем которой равен V то:
mV f ( x; y; z)dV MV
V
где m и M соответственно наименьшее и наибольшее
значение подынтегральной функции в области V.
7
Если функция f(x; y; z) непрерывна в замкнутой области ,
объем которой равен V, то в этой области существует такая
точка М0 (x0 ; y0 ; z0 ), что
f ( x; y; z)dV f ( x ; y ; z ) V
0
V
0
0
Среднее значение
функции f в области V

7. Вычисление тройного интеграла в декартовых координатах

7/14
Пусть областью интегрирования V является область, ограниченная
сверху поверхностью z = z2(x; y),
z = z2(x; y)
z
снизу поверхностью z = z1(x; y),
сбоку цилиндрической поверхностью,
причем z1(x; y) и z2(x; y) –
непрерывные функции,
удовлетворяющее условию:
z1( x; y ) z2 ( x; y ),
z = z1(x; y)
0
проекциями которых на
плоскость XOY является
область D.
y
D
x

8. Вычисление тройного интеграла в декартовых координатах

8/14
Вычисление тройного интеграла в
декартовых координатах
Будем считать область V – правильной относительно оси OZ:
любая прямая, параллельная оси OZ
пересекает границу области не более
чем в двух точках
Тогда для любой непрерывной
в области V функции f(x; y; z)
имеет место формула,
сводящая вычисление тройного
интеграла к вычислению
двойного интеграла от
однократного.
z = zz2(x;
y)
2(x;y)
z
z =zz1(x;
y)
1(x;y)
0
x
f
(
x
;
y
;
z
)
dV
V
D
dS
f
(
x
;
y
;
z
)
dz
y
D

9. Вычисление тройного интеграла в декартовых координатах

9/14
Пусть область D ограничена прямыми x = a, x = b (a < b) и
кривыми y = φ1(x), y = φ2(x), причем функции φ1(x) и φ2(x)
непрерывны и таковы, что
1( x ) 2 ( x )
x a, b
y = φ22(x
(x))
y
Тогда, переходя от двойного интеграла по
области D к двукратному, получим
формулу, по которой вычисляется
тройной интеграл в декартовых
координатах
z2 ( x ; y )
D
y =φφ11(x)
(x)
0
aa
f ( x; y; z)dV dx dy f ( x; y; z) dz
V
z1 ( x ;y )
b
x

10. Вычисление тройного интеграла в декартовых координатах

b
2 ( x )
z2 ( x ; y )
a
1( x )
z1 ( x ;y )
10/14
f ( x; y; z)dV dx dy f ( x; y; z) dz
V
Сначала вычисляется внутренний интеграл по переменной z при
постоянных x и y. Результат вычисления этого интеграла есть
функция двух переменных x и y.
Дальнейшее решение аналогично вычислению двукратного
интеграла.
Замечания
1 Если область V более сложная, чем рассмотренная, то ее
следует разбить на конечное число правильных областей.
2
Порядок интегрирования в формуле при определенных
условиях может быть иным.

11. Вычисление тройного интеграла в декартовых координатах

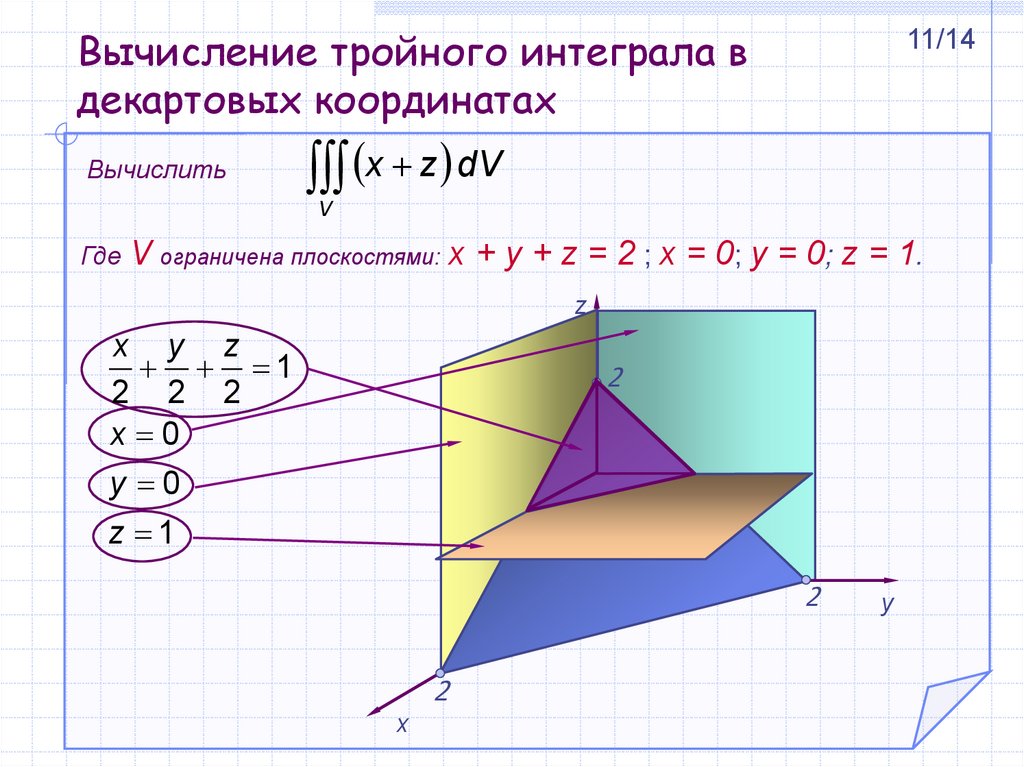
Вычислить
11/14
x z dV
V
Где V ограничена плоскостями: x + y + z = 2 ; x = 0; y = 0; z = 1.
z
x y z
1
2 2 2
x 0
y 0
z 1
2
1
0
2
x
2
y

12. Вычисление тройного интеграла в декартовых координатах

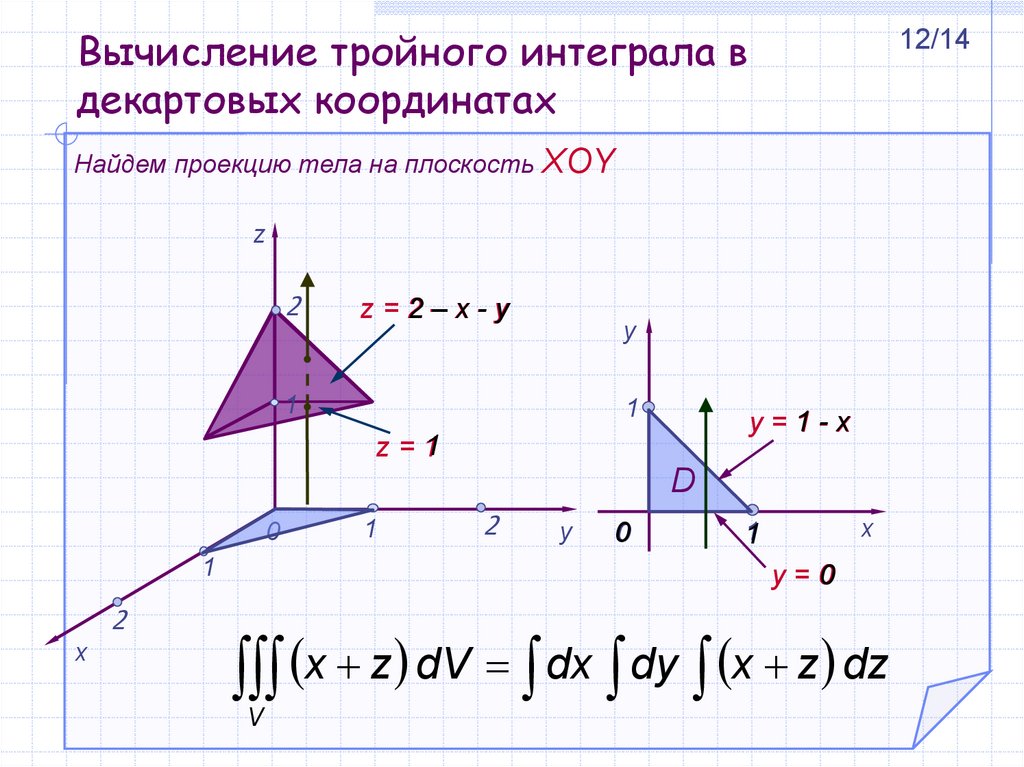
12/14
Найдем проекцию тела на плоскость XOY
z
2
z=2–x-y
y
1
1
y=1-x
z=1
D
0
1
2
x
1
2
y
0
x
1
y=0
x z dV dx dy x z dz
V

13. Вычисление тройного интеграла в декартовых координатах

1 x
2 x y
1 x
2 x y
z
0 dx 0 dy 1 x z dz dx dy xz 2
0
0
1
1
1
2
13/14
2
2
x
y
1
( x ) dy
0 dx 0 x(2 x y )
2
2
1
1 x
1 x
2
2
x
y
1
2
0 dx 0 2x x xy 2 2x 2y 2 xy 2 x 2 dy
1
1 x
x2
y 2 3
0 dx 0 x 2 2y 2 2 dy
1

14. Вычисление тройного интеграла в декартовых координатах

14/14
1 x
x y
y
3
2
0 xy 2 y 6 2 y dx
0
1
2
3
3
x 2 (1 x )
(
1
x
)
3
2
x(1 x )
(1 x )
(1 x ) dx
2
6
2
0
1
3
5
1 2 1 3 3
(
1
x
)
x x x (1 x )2
dx
2
2
2
2
6
0
1
1
5 2 1 3 1 4 3
(1 x ) (1 x )
x x x x
6
8
2
3
24 0
4
5 1 1 3 1 1 1
4 6 8 2 3 24 4
3
4