Похожие презентации:
Применение интегралов в экономике
1. Применение интегралов в экономике
Выполнил Алексанин С.В.2. Применение интегрального исчисления к решению прикладных задач в экономике
Нет ни одной области математики, какбы абстрактна она ни была, которая
когда-нибудь не окажется применимой к
явлениям действительного мира.
Н. И. Лобачевский
3.
1)1
x
2
dx
1
2)
3)
3
0
3 1
2 2
6
И
К
cos xdx
1
5e dx
x
0
4)
3
dx
1 x 2
ln 5
З
5e 5e 5
В
2
3
А Н
4.
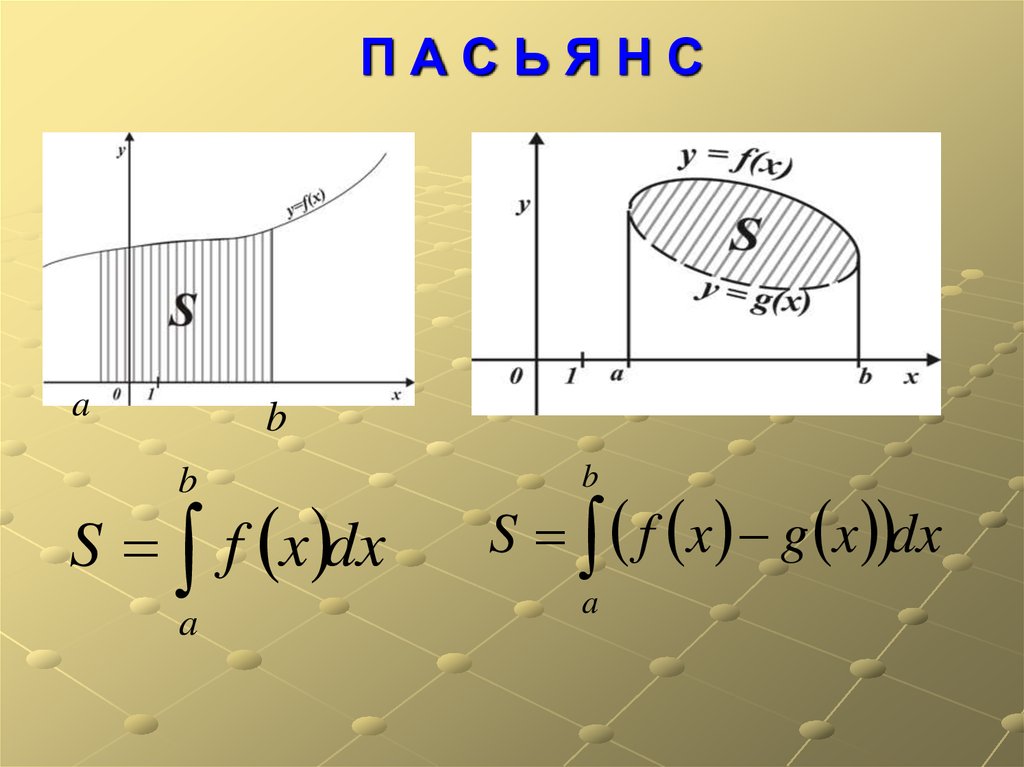
ПАСЬЯНСa
b
b
S f x dx
a
b
S f x g x dx
a
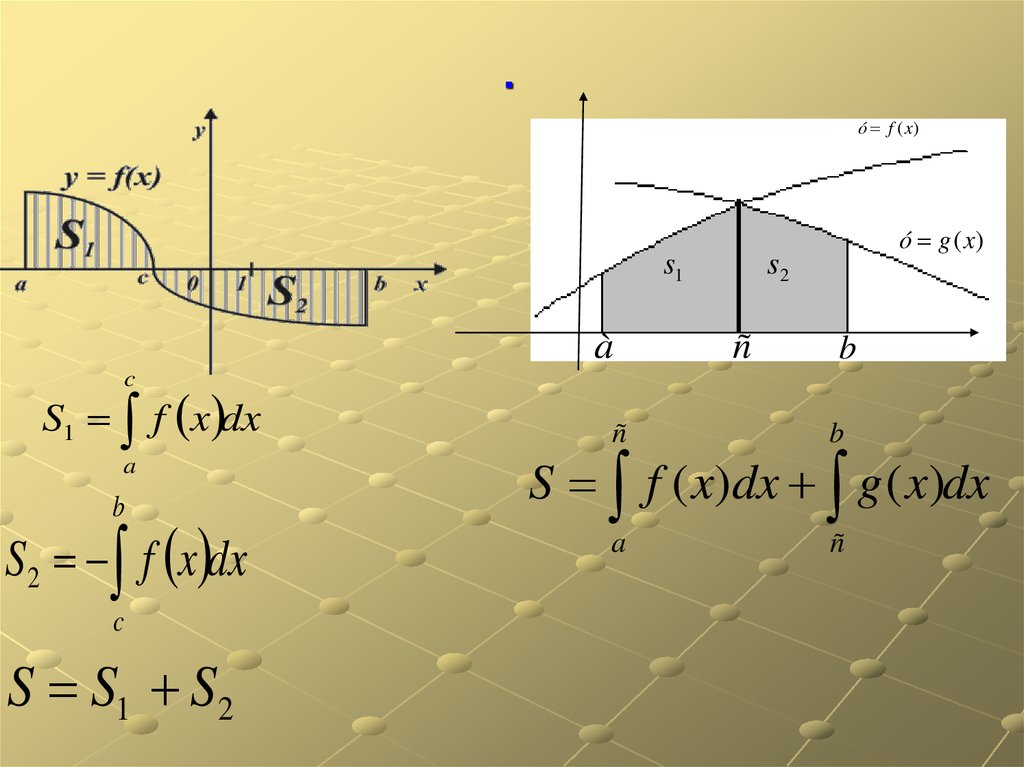
5.
.ó f (x)
s1
à
ó g (x)
s2
ñ
b
c
S1 f x dx
a
b
S 2 f x dx
c
S S1 S2
ñ
b
a
ñ
S f ( x)dx g ( x)dx
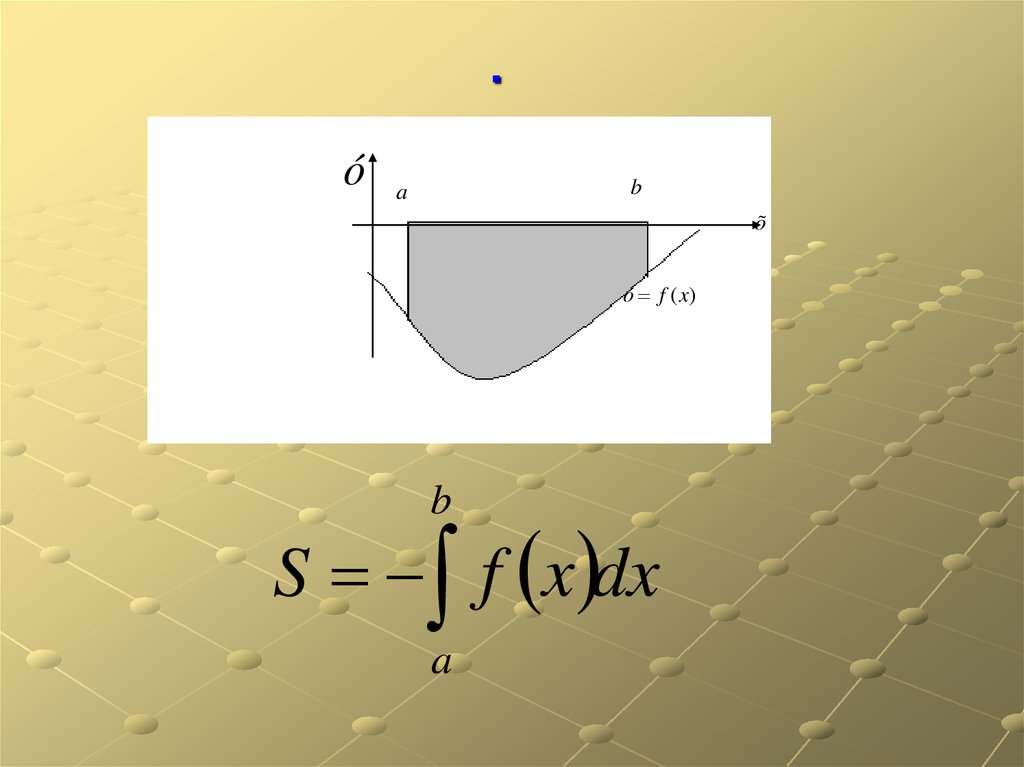
6.
.ó
b
a
õ
ó f (x)
b
S f x dx
a
7.
Интегральное исчисление в экономикеиспользуют для прогнозирования материальных
затрат. При прогнозировании материальных
затрат часто возникает необходимость
вычисления площадей сложных фигур.
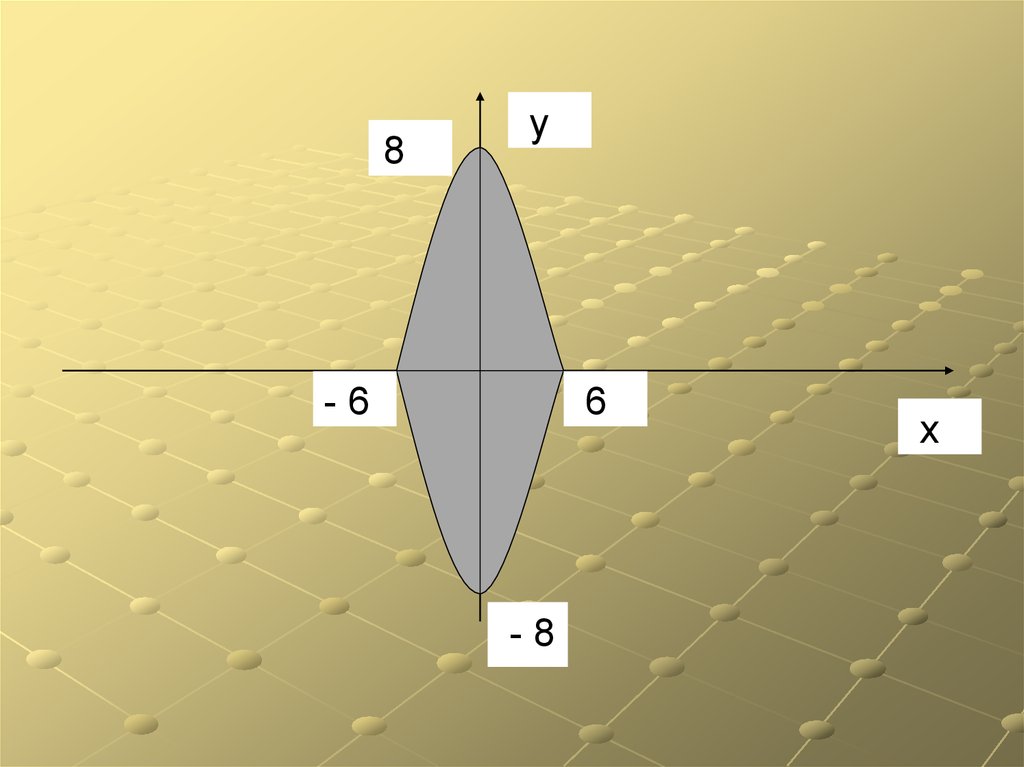
Я хочу открыть магазин «Рыболовный
рай», в котором будут продаваться
товары для рыбалки и отдыха.
Торговый зал напоминает палубу
корабля, наибольшее расстояние
вдоль зала составляет 16 метров,
наибольшее расстояние поперёк зала
– 12 метров. Помогите рассчитать его
площадь.
8.
8у
-6
6
-8
х
9.
Я являюсь директором магазинабытовой химии и косметики «Уют
плюс». Можно ли определить запас
товаров в магазине, образуемый за
некоторое количество дней?
10.
Если непрерывная функция f(t) характеризуетпоступление товара в зависимости от времени t,
то запас товаров в магазине за промежуток
времени от t1 до t2 будет выражаться формулой
11. П р и м е р
ПримерОпределите запас товаров в
магазине, образуемый за три дня,
если поступление товаров
характеризуется функцией
f(t) = 2t + 5, t – время.
12.
Я – директор сети магазинов«Мегаспорт». Стараюсь вести
грамотную ценовую политику. Знаю,
что для снижения цен на товары
необходимо рассчитывать
потребительский излишек. Помогите
разобраться в этом вопросе.
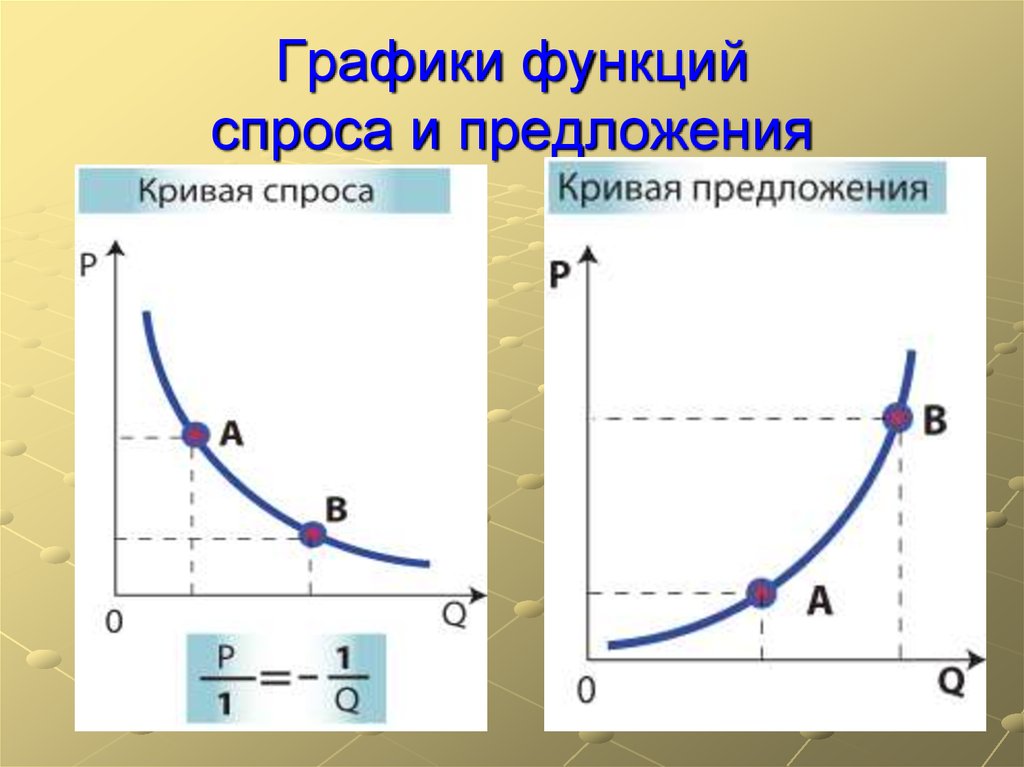
13. Графики функций спроса и предложения
14.
15.
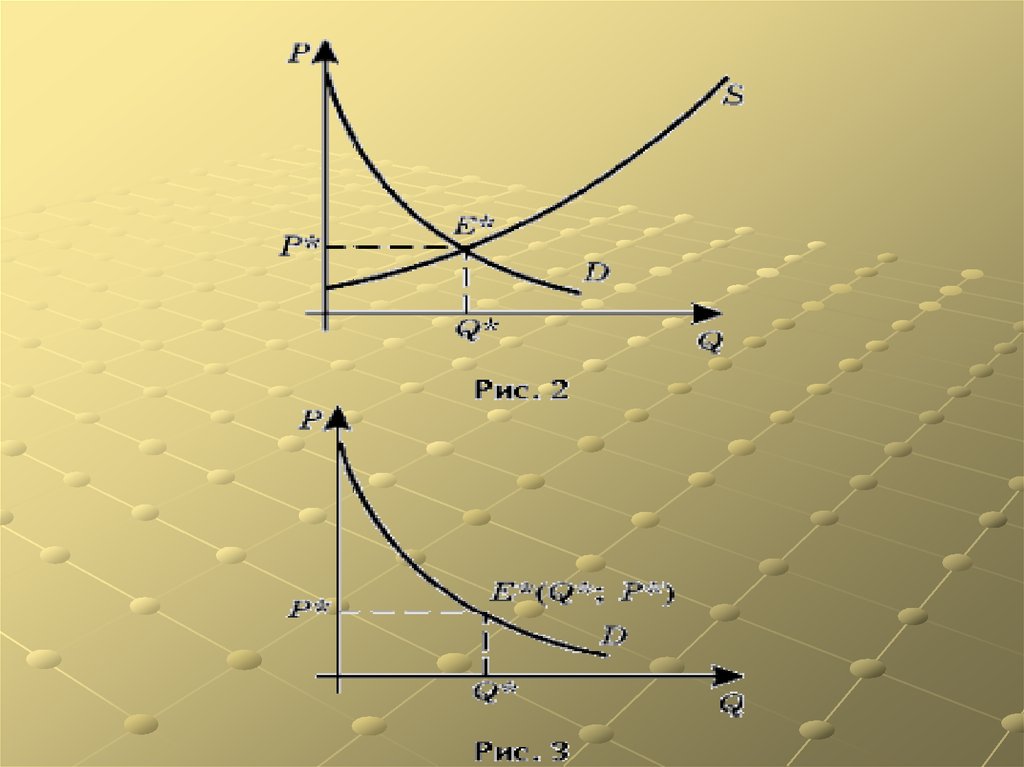
Пусть p = f (q) – функция спроса, где q –количество товара (в ед.), p – цена единицы
товара (в руб.). Тогда, потребительский
излишек можно посчитать по следующей
формуле
Q
*
0
f (q )dq P Q
*
*
16. П р и м е р
ПримерСпрос на некоторый товар задается
функцией p = 4– q2, где q – количество
товара (в ед.), p – цена единицы товара
(в руб.), а равновесие на рынке данного
товара достигается при p*=q*=1.
Определите величину потребительского
излишка.


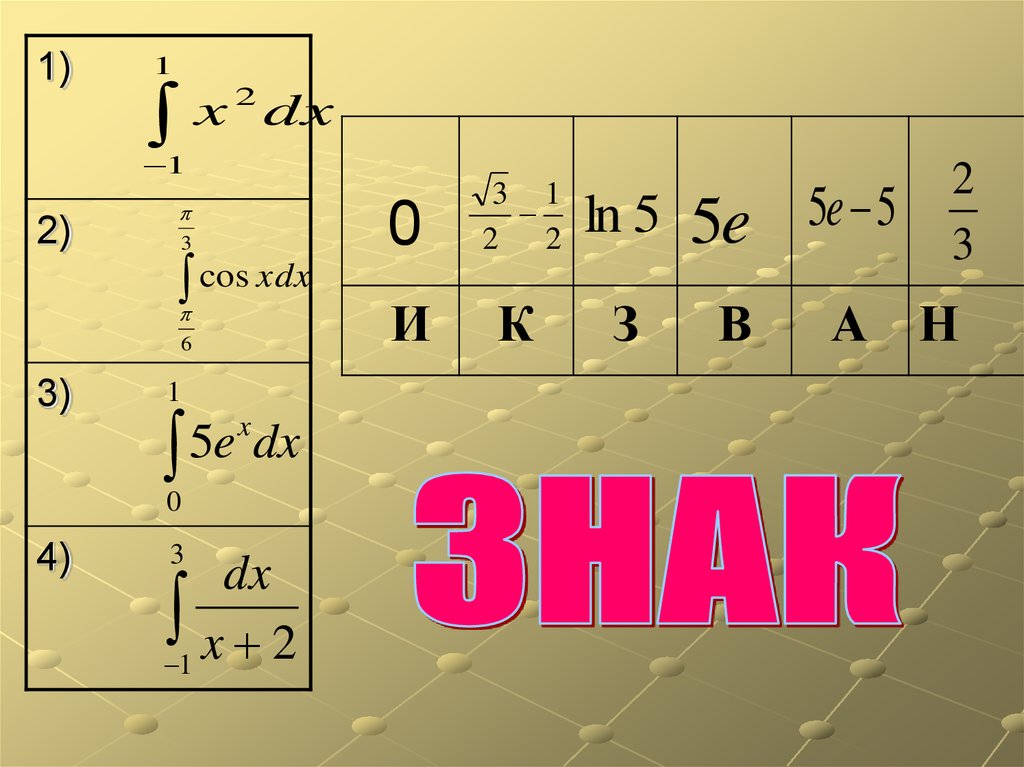







 Экономика
Экономика








