Похожие презентации:
Общий алгоритм вычисления корреляции и различий
1.
ОБЩИЙ АЛГОРИТМ РАСЧЕТА КОРРЕЛЯЦИИ ИРАЗЛИЧИЙ
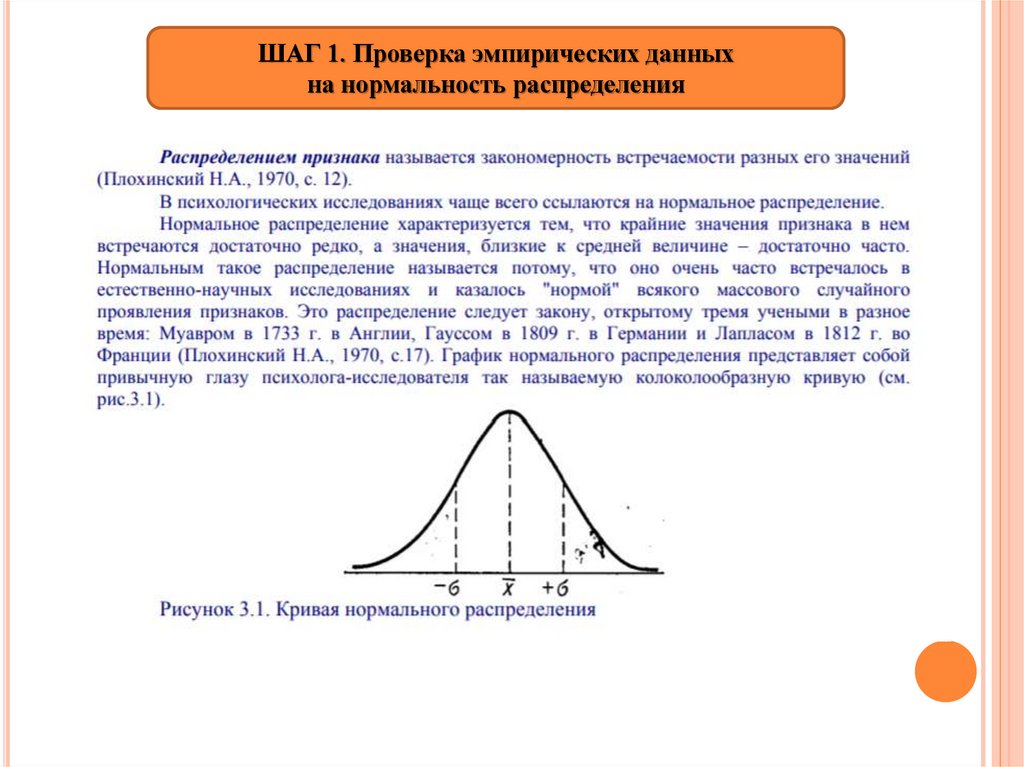
ШАГ 1. Проверка эмпирических данных
на нормальность распределения
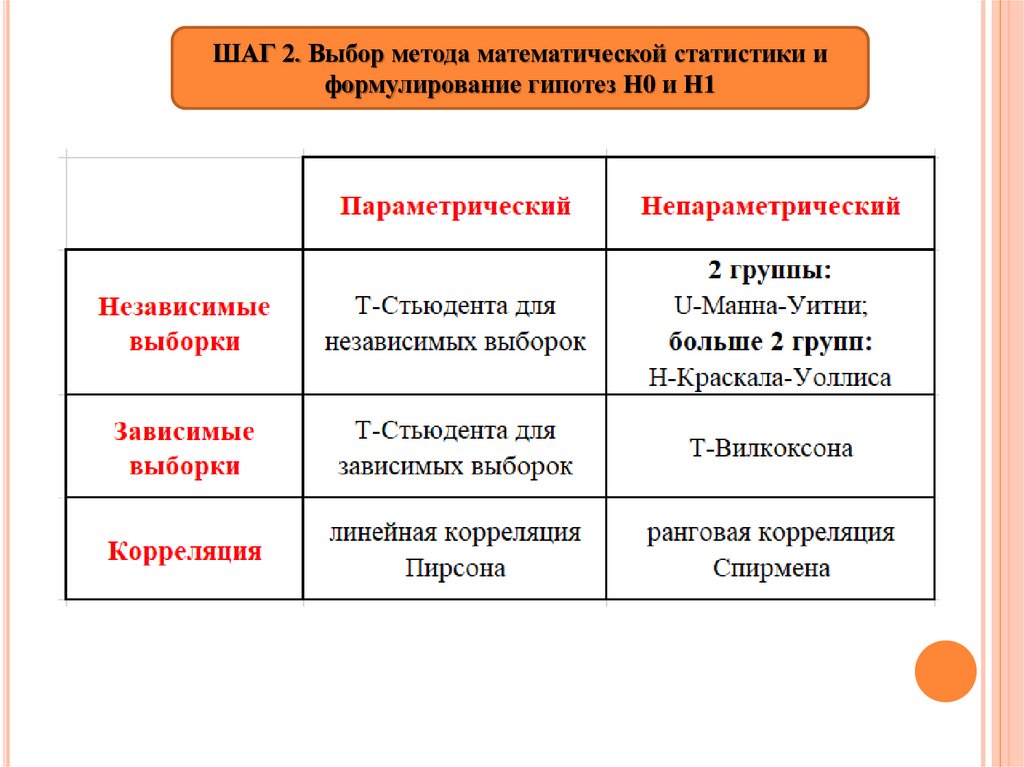
ШАГ 2. Выбор метода математической статистики и
формулирование гипотез H0 и H1
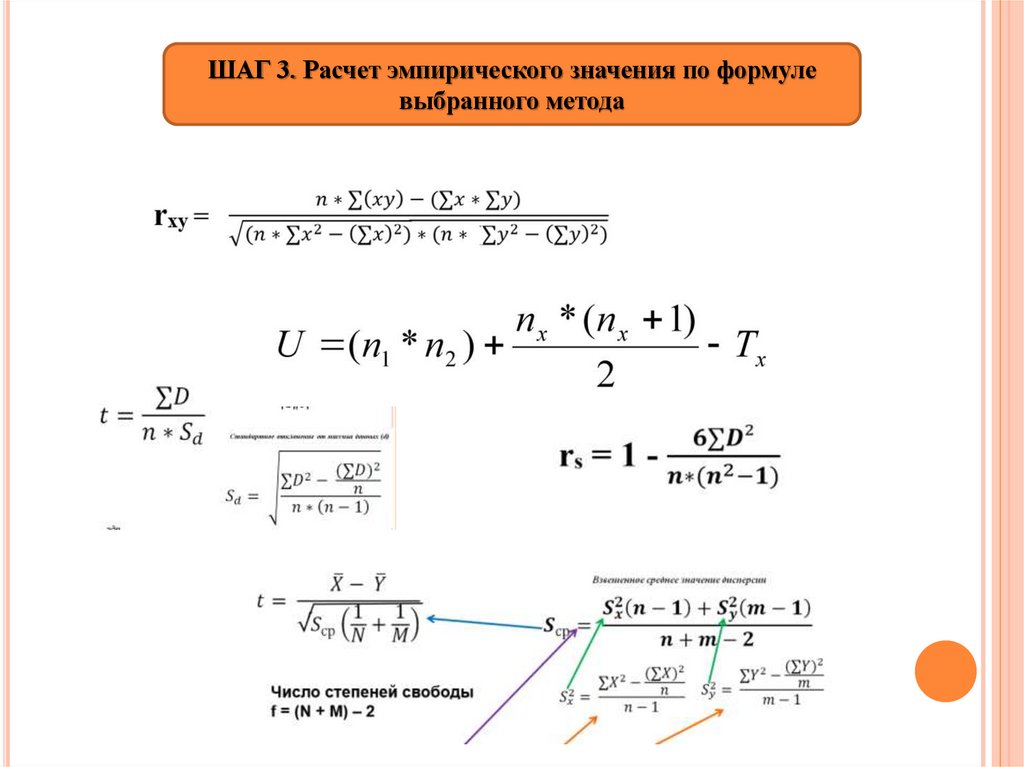
ШАГ 3. Расчет эмпирического значения по формуле
выбранного метода
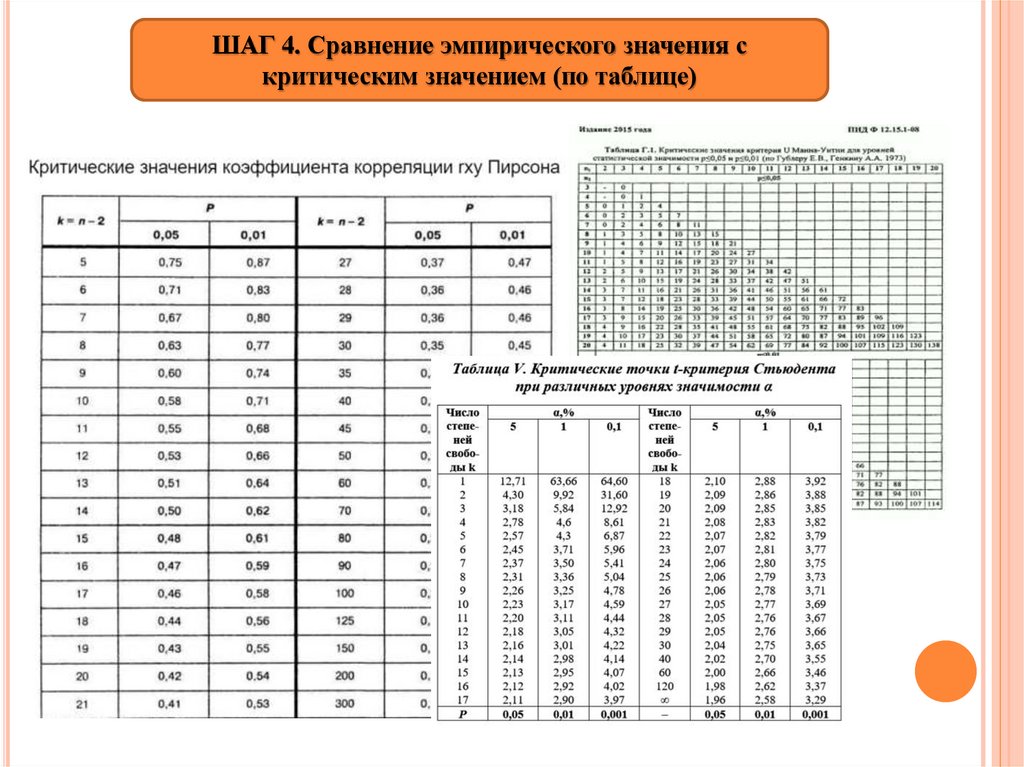
ШАГ 4. Сравнение эмпирического значения с
критическим значением (по таблице)
ШАГ 5. Формулирование вывода
2.
ШАГ 1. Проверка эмпирических данныхна нормальность распределения
3.
ЗАЧЕМ ЗНАТЬ, ЯВЛЯЕТСЯ ЛИРАСПРЕДЕЛЕНИЕ НОРМАЛЬНЫМ?
ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
(КОЭЭФИЦИЕНТ КОРРЕЛЯЦИИ
ПИРСОНА, КРИТЕРИЙ
СТЬЮДЕНТА)
Требуют, чтобы эмпирические данные соответствовали
закону нормального распределения.
Более мощные по сравнению с непараметрическими, но не
работают, если распределение данных не является
нормальным.
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
(КОЭЭФИЦИЕНТ КОРРЕЛЯЦИИ
СПИРМЕНА, КРИТЕРИИ МАННА-УИТНИ,
КРАСКАЛА-УОЛЛИСА, ВИЛКОКСОНА)
Не требуют, чтобы эмпирические данные соответствовали
закону нормального распределения.
Менее мощные по сравнению с параметрическими.
4.
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯAx – коэффициент асимметрии, Ex – коэффициент
По Н. А. Плохинскому:
эксцесса
Распределение НЕНОРМАЛЬНО, если:
По Е. И. Пустыльнику:
5.
ШАГ 2. Выбор метода математической статистики иформулирование гипотез H0 и H1
6.
ШАГ 2. Выбор метода математической статистики иформулирование гипотез H0 и H1
Н0 (нулевая гипотеза):
корреляция/различия между двумя признаками
не является статистически значимой
(корреляции/различий нет)
Н1 (альтернативная гипотеза):
корреляция/различия между двумя признаками
является статистически значимой
(корреляции/различия есть)
7.
ШАГ 3. Расчет эмпирического значения по формулевыбранного метода
8.
ШАГ 4. Сравнение эмпирического значения скритическим значением (по таблице)
9.
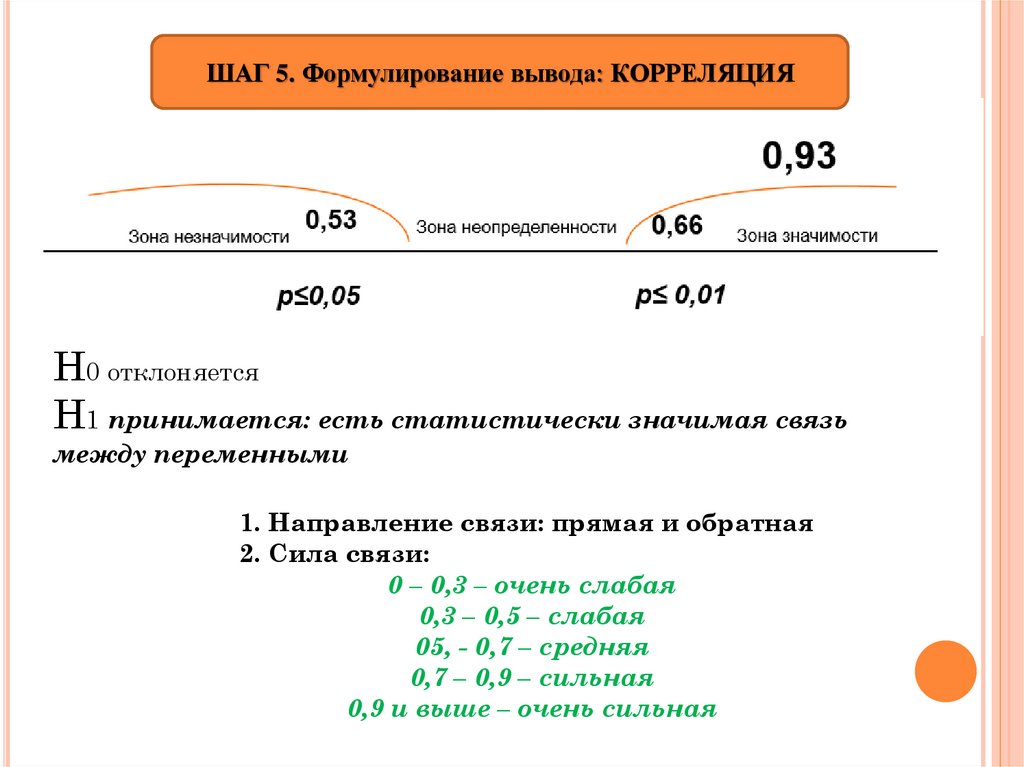
ШАГ 5. Формулирование вывода: КОРРЕЛЯЦИЯН0 отклоняется
Н1 принимается: есть статистически значимая связь
между переменными
1. Направление связи: прямая и обратная
2. Сила связи:
0 – 0,3 – очень слабая
0,3 – 0,5 – слабая
05, - 0,7 – средняя
0,7 – 0,9 – сильная
0,9 и выше – очень сильная
10.
ШАГ 5. Формулирование вывода: РАЗЛИЧИЯСРАВНИТЬ ЭМПИРИЧЕСКОЕ ЗНАЧЕНИЕ С
КРИТИЧЕСКИМ И В ЗАВИСИМОСТИ ОТ ЭТОГО,
ОПРЕДЕЛИТЬ, НУЖНО ПРИНЯТЬ Н0 ИЛИ Н1.





 Математика
Математика








