Математическое ожидание и дисперсия случайной величины «число успехов в серии испытаний Бернулли

1.

Математическое ожидание и
дисперсия случайной величины.
Математическое ожидание и
дисперсия случайной величины
«число успехов в серии
испытаний Бернулли

2.

Математическое ожидание играет важную роль в области
математической статистики и теории вероятностей. Оно
представляет собой среднее значение случайной величины и
помогает предсказать, какие значения можно ожидать в будущем.
Математическое ожидание находит применение во многих сферах
— от физики и экономики до компьютерных наук и биологии.

3.

Предположим, у нас есть случайная величина X.
Её математическое ожидание можно обозначить
как E(X) или EX.
Пусть распределение случайной величины X задано
таблицей.
Значение
величины X
x1
x2
x3
...
xn
Вероятность
p1
p2
p3
...
pn
Математическим ожиданием случайной величины X называют
число EX=x1⋅p1+x2⋅p2+x3⋅p3+...+xn⋅pn.

4.

Математическое ожидание EX называют
также ожидаемым значением случайной
величины X, средним значением
случайной величины X.
Математическое ожидание случайной величины, которая
имеет измеряемые значения в определённых единицах, также
будет измеряться в указанных единицах.
Например, для случайной величины «вес» математическое
ожидание будет выражено в килограммах, а для случайной
величины «рост» — в сантиметрах.
Это связано с тем, что значения случайной величины и её
математического ожидания согласуются в одних и тех же
единицах измерения.

5.

Пример:
Предположим, что мы выбираем случайную величину X в
качестве числа очков, которые выпали на одной игральной
кости.
Вероятность выпадения каждой грани одинакова
и равна 1/6.
Представим ситуацию, в которой каждое значение случайной
величины имеет одинаковую вероятность появления. В таком
случае математическое ожидание можно определить как
просто среднее арифметическое всех значений. Этот пример
наглядно демонстрирует эту концепцию.

6.

Найдём математическое ожидание выигрыша, рассмотрев пример
с расчётом цены лотерейного билета.
Пример:
Для проведения лотереи было изготовлено 200 билетов,
из которых один билет имеет выигрыш в
размере 1000 рублей, 20 билетов имеют выигрыш в
размере 1500 рублей, а остальные билеты не имеют
выигрышей. Для определения выигрыша выбирается один
билет случайным образом.
Эта случайная величина может принимать три
значения: 1000, 1500 и 0 руб. (нет выигрыша).

7.

Пример:
Их вероятности равны:
Тогда математическое ожидание выигрыша
равно EX=1000⋅0,005+1500⋅0,1+0⋅0,895= 155 руб.
Получается, что средний выигрыш на один билет
равен 155 рублей.
Для того чтобы обеспечить доходы организаторов, лотерея
должна иметь более высокую цену билета, чем средний
выигрыш.

8.

Давай рассмотрим пример, который демонстрирует использование
математического ожидания для определения стоимости страхового полиса
ОСАГО.
Полис ОСАГО обязателен для всех владельцев автомобилей и предназначен
для покрытия гражданской ответственности. Его можно приобрести у страховых
компаний, которые берут на себя обязательство в случае ДТП возместить ущерб,
который автовладелец причинит окружающим.
В Государственной Думе проходили обсуждения стоимости полиса и пределов
выплат.
Для определения стоимости полиса необходимо знать две величины:
вероятность, с которой автовладелец может причинить ущерб окружающим в
результате ДТП в течение года, и среднюю сумму ущерба. Перемножение этих
величин позволяет получить средний размер страховой премии компании на один
застрахованный автомобиль.
Каждая выплата для отдельного автомобиля является случайной величиной.
Стоимость полиса состоит из математического ожидания страховой выплаты и
дохода страховой компании.

9.

Пример:
Страховой полис ОСАГО в страховой компании
стоит 35000 рублей. По статистике в течение года
владелец автомобиля попадает в мелкую аварию с
вероятностью 0,15, и средняя сумма страховой выплаты
при этом равна 50000 рублей.
С вероятностью 0,027 автомобиль попадает в серьёзную
аварию, и средняя сумма выплаты при этом
будет 600000 рублей.
Для начала найдём математическое ожидание случайной
величины «средняя сумма страховой
выплаты»: 50000⋅0,15+600000⋅0,027 = 23700 руб.
Затем найдём «средний доход страховой компании от
продажи одного полиса», зная, что страховой полис
ОСАГО стоит 35000 руб.: 35000−23700 = 11300 руб.

10.

Свойства математического ожидания
Свойство 1.
Пусть математическое ожидание случайной
величины X равно EX. Если a — произвольное число,
то E(X+a)=EX+a.
Свойство 2.
Пусть математическое ожидание случайной
величины X равно EX. Если b — произвольное число,
то E(bX)=b⋅EX.
Свойство 3.
Пусть X и Y — две случайные величины, которые имеют
математические ожидания. Тогда E(X+Y)=EX+EY.

11.

Пример:
В настольных играх, где игроки бросают игральную кость по
очереди, фишка игрока движется по игровому полю в
зависимости от выпавших очков. Если мы спросим, насколько
далеко игрок сможет продвинуться за десять ходов, точного
ответа мы не получим. Возможно, игрок сможет продвинуться
на 60 шагов, если выпадет десять шестёрок подряд. Но такая
ситуация встречается крайне редко. Также редко выпадает
десять единиц подряд. Вероятнее всего, за десять бросков на
кости будут разные значения.
Например, результаты десяти бросков могут выглядеть
так: 5;6;3;6;4;1;4;6;3;2 — или так: 1; 2; 6; 3; 1; 3; 4; 2; 2; 5.
Сумма очков во второй серии из десяти бросков составляет 29,
а в первой серии сумма равна 40.
Возможно ли предсказать, какая будет средняя сумма?

12.

Пример:
Среднюю сумму можно теоретически вычислить как
математическое ожидание случайной величины.
Сумма числа очков на кости во время каждого броска,
обозначенная через S, может быть выражена через
X1,X2,X3,...,X10.
Тогда
E(S)=E(X1+X2+X3+...+X10)=E(X1)+E(X2)+...+E(X10)=
=10⋅1+2+3+4+5+66=10⋅3,5=35.
Между наименьшим возможным продвижением на 10 шагов и
наибольшим возможным на 60 лежит число, которое мы
получили.

13.

Речь идёт о теории вероятностей, где случайные величины играют
важную роль. Они имеют возможность принимать разные значения,
и нам нужно уметь описывать их среднее значение и рассеивание.
При анализе описательной статистики мы обсуждали понятия
среднего арифметического и дисперсии числовых наборов.
Дисперсия числового ряда показывает разброс данных. Если
дисперсия меньше, то, значит, разброс значений тоже меньше. В то
же время, чем больше дисперсия, тем больше разброс значений.
Для описания среднего значения случайной
величины применяется математическое ожидание.
А для описания рассеивания чаще всего используется дисперсия
случайной величины.
Обозначают дисперсию случайной величины D(X) или DX.

14.

Дисперсией случайной величины X называется
математическое ожидание случайной
величины (X−EX)2: DX=E((X−EX)2).
Дисперсия случайной величины
равна среднему квадрату отклонения
этой случайной величины от своего среднего.
Очевидно, что DX≥0. Чем меньше дисперсия, тем более кучно
значения случайной величины группируются около
математического ожидания EX.
Если же DX=0, то случайная величина X принимает единственное
значение. В таком случае говорят, что случайная величина
постоянна.

15.

Найдём дисперсию случайной величины X «число очков при
однократном броске кубика».
Нам известно, что EX=3,5.
Построим распределение случайной величины X−EX.
Значение
−2,5
−1,5
−0,5
0,5
1,5
2,5
Вероятность
1/6
1/6
1/6
1/6
1/6
1/6

16.

Отметим особенность дисперсии: она измеряется не в тех
единицах, что сама случайная величина. Если случайная
величина измеряется в метрах, то дисперсия — в метрах
квадратных и т. д. Это часто бывает неудобно.
Поэтому используют стандартное отклонение случайной
величины, для того чтобы рассеивание выразить в тех же
единицах, в каких выражается случайная величина.
Стандартным отклонением случайной
величины X называется квадратный корень из
дисперсии

17.

Существует более простая формула для вычисления
дисперсии, которая обычно удобнее: DX=EX2−E2X.
Нам понадобятся ещё некоторые свойства дисперсии.
Свойство 1.
Пусть случайная величина X имеет дисперсию DX, и
пусть a — произвольное число.
Тогда D(X+a)=DX.
При сдвиге значений дисперсия случайной величины не
меняется.
Свойство 2.
Пусть случайная величина X имеет дисперсию DX, и
пусть b — произвольное число.
Тогда D(bX)=b2DX.

18.

Пример:
Дисперсия случайной величины X равна 5.
Найдём дисперсию случайной величины Y=3−4X.
Используя свойство 1:
DY=D(3−4X)=D(−4X).
По свойству 2:
D(−4X)=(−4)2DX=16⋅5=80.

19.

Свойство 3.
Пусть случайные X и Y независимы и их
дисперсии равны DX и DY.
Тогда D(X+Y)=DX+DY.
Данное свойство верно не только для двух, но и для
произвольного числа независимых случайных величин.
Это очень важное и интересное свойство. Дисперсии
независимых случайных величин можно складывать.
Дисперсия суммы независимых величин равна
сумме их дисперсий.
Это свойство отчасти объясняет, почему дисперсия стала
наиболее употребительной мерой рассеивания.

20.

Теоремы, которые позволяют находить математическое
ожидание и дисперсию числа попыток в испытаниях до первого
успеха.
Теорема 1.
Если вероятность успеха в каждом отдельном испытании равна p,
то математическое ожидание случайной величины X «число
испытаний до первого успеха» равно
Теорема 2.
Если вероятность успеха в каждом отдельном испытании равна p,
то дисперсия случайной величины X «число испытаний до
первого успеха» равна
Следовательно, стандартное отклонение равно

21.

Задание № 1
Бинарная случайная величина I принимает
значения 0 и 1 с вероятностями q и p
соответственно.
Найди математическое ожидание EX,
если p = 0,59.

22.

Задание № 2
Найди математическое ожидание суммы очков,
выпадающих на четырёх кубиках при одном
броске.

23.

Задание № 3
В таблице дано распределение вероятностей случайной
величины.
Значение
−5
−4
−2
1
4
Вероятность
0,06
0,19
0,07
0,13
0,55
Найди математическое ожидание этой величины.

24.

Задание № 4
Математическое ожидание случайной
величины Y равно 28.
Найди математическое ожидание случайной
величины:
1. 6-6Y
2. 1,3Y-3,5

25.

Задание № 5
Найди стандартное отклонение
случайной величины, если её
дисперсия равна 5,76.

26.

Задание № 6
Стандартное отклонение случайной
величины равно 17,8.
Найди дисперсию этой случайной
величины.

27.

Задание № 7
В таблице дано распределение вероятностей
случайной величины X.
Значение X
−7
−3
5
8
Вероятность
0,03
0,06
0,25
0,66
Пользуясь упрощённой формулой для нахождения
дисперсии величины X, вычисли её.
(При необходимости ответ округли до сотых.)

28.

Задание № 8
Дано распределение случайной величины X.
Значение
−3
−2
2
5
6
Вероятность
0,15
0,06
0,05
0,21
0,53
Найди стандартное отклонение случайной величины X.
(Все вычисления округляй до сотых.)

29.

Задание № 9
Случайная величина Y принимает все целые значения
от −3 до 5 с равными вероятностями.
Найди её математическое ожидание.

30.

Домашнее задание
Задание № 1
Бинарная случайная величина I принимает
значения 0 и 1 с вероятностями q и p
соответственно.
Найди математическое ожидание EX,
если q = 0,02.

31.

Домашнее задание
Задание № 2
Найди математическое ожидание суммы очков,
выпадающих на четырёх пяти кубиках при
одном броске.

32.

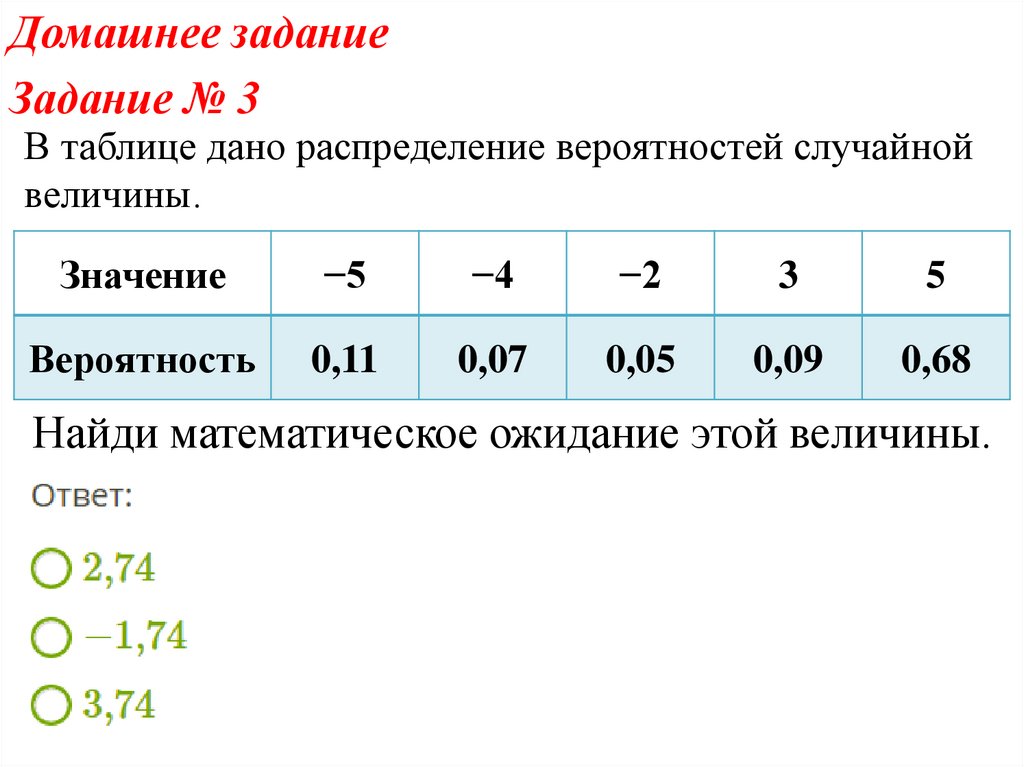
Домашнее задание
Задание № 3
В таблице дано распределение вероятностей случайной
величины.
Значение
−5
−4
−2
3
5
Вероятность
0,11
0,07
0,05
0,09
0,68
Найди математическое ожидание этой величины.

33.

Домашнее задание
Задание № 4
Найди стандартное отклонение
случайной величины, если её дисперсия
равна 3,24.