Математическая логика

1.

матлогика №1 5

2.

делимость
2
1
разбор
неравенств
а
2
1
разбор
поразрядная конъюнкция
2
1
разбор
множеств
а
2
1
разбор
отрезки
2
1
разбор
смешанные
1
2

3.

15-е номера разобраны
отдыхать?

4.

пошагово разберём задачу на
делимость
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без
остатка на натуральное число m». Для какого наименьшего натурального числа
А формула
(A + x < 123) → (ДЕЛ(x, 5) → ¬ДЕЛ(x, 7))
тождественно истинна (т.е. принимает значение 1) при любом натуральном
значении переменной х?

5.

1) Сначала создаём функцию от всех неизвестных и возвращаем выражение
из условия:
def f(x, a):
return (a + x < 123) <= ((x % 5 == 0) <= (x % 7 != 0))

6.

2) Создаём цикл, чтобы перебрать натуральные A:
def f(x, a):
return (a + x < 123) <= ((x % 5 == 0) <= (x % 7 != 0))
for a in range(1, 10000):

7.

3) Внутри цикла пишем проверку, с помощью конструкции all, проверяем, что
при всех перебираемых натуральных значениях x значение функции будет
истиной:
def f(x, a):
return (a + x < 123) <= ((x % 5 == 0) <= (x % 7 != 0))
for a in range(1, 10000):
if all(f(x, a) == 1 for x in range(1, 3000)):

8.

4) Если условие сработало, то выводим это число A
def f(x, a):
return (a + x < 123) <= ((x % 5 == 0) <= (x % 7 != 0))
for a in range(1, 10000):
if all(f(x, a) == 1 for x in range(1, 3000)):
print(a)

9.

5) Так как нужно найти минимальное A, после первого найденного числа
прерываем перебор, с помощью break:
def f(x, a):
return (a + x < 123) <= ((x % 5 == 0) <= (x % 7 != 0))
for a in range(1, 10000):
if all(f(x, a) == 1 for x in range(1, 3000)):
print(a)
break
ответ
88

10.

1
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без
остатка на натуральное число m». Для какого наименьшего натурального числа
А формула
(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) \/ (x + A ≥ 100)
тождественно истинна (т.е. принимает значение 1) при любом натуральном
значении переменной х?
пояснение
ответ
94

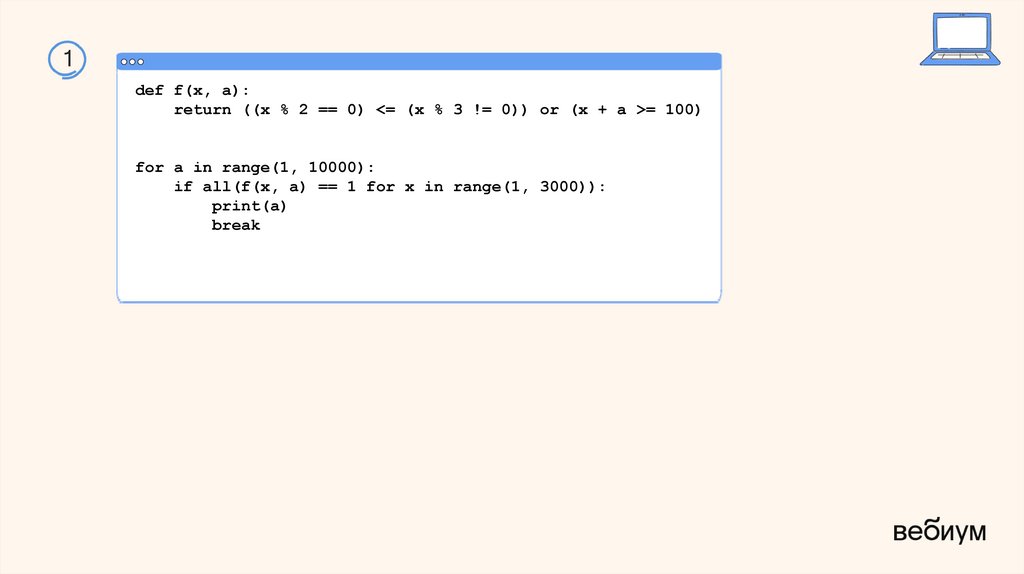
11.

1
def f(x, a):
return ((x % 2 == 0) <= (x % 3 != 0)) or (x + a >= 100)
for a in range(1, 10000):
if all(f(x, a) == 1 for x in range(1, 3000)):
print(a)
break

12.

2
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без
остатка на натуральное число m». Для какого наибольшего натурального числа
А формула
(ДЕЛ(x, 3) → ¬ДЕЛ(x, 2)) ∨ (x - A ≥ 4)
тождественно истинна (т.е. принимает значение 1) при любом натуральном
значении переменной х?
пояснение
ответ
2

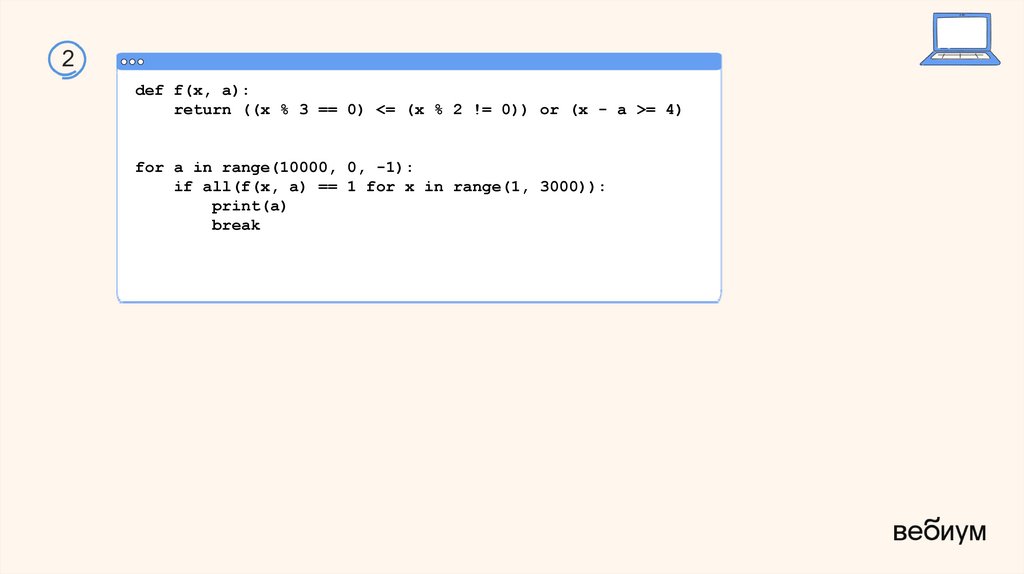
13.

2
def f(x, a):
return ((x % 3 == 0) <= (x % 2 != 0)) or (x - a >= 4)
for a in range(10000, 0, -1):
if all(f(x, a) == 1 for x in range(1, 3000)):
print(a)
break

14.

пошагово разберём задачу на
неравенства
Для какого наибольшего целого
неотрицательного числа А выражение
(x * y > A) \/ (x > y) \/ (74 > x)
тождественно истинно, то есть принимает значение 1 при любых целых
неотрицательных x и y?

15.

1) Сначала создаём функцию от всех неизвестных и возвращаем выражение
из условия:
def f(x, y, a):
return (x * y > a) or (x > y) or (74 > x)

16.

2) Перебираем число A, так как нужно наибольшее, то перебор начнём в
порядке убывания:
def f(x, y, a):
return (x * y > a) or (x > y) or (74 > x)
for a in range(10000, -1, -1):

17.

3) Внутри цикла пишем проверку, с помощью конструкции all, проверяем, что
при всех перебираемых неотрицательных значениях (включая ноль) x и y
значение функции будет истиной. 200 будет достаточно, так как это 200 * 200
комбинаций:
def f(x, y, a):
return (x * y > a) or (x > y) or (74 > x)
for a in range(10000, -1, -1):
if all(f(x, y, a) == 1 for x in range(200) for y in range(200)):

18.

4) Если условие сработало, то выводим это число A
def f(x, y, a):
return (x * y > a) or (x > y) or (74 > x)
for a in range(10000, -1, -1):
if all(f(x, y, a) == 1 for x in range(200) for y in range(200)):
print(a)

19.

5) Так как нужно найти максимальное A, после первого найденного числа
прерываем перебор, с помощью break:
def f(x, y, a):
return (x * y > a) or (x > y) or (74 > x)
for a in range(10000, -1, -1):
if all(f(x, y, a) == 1 for x in range(200) for y in range(200)):
print(a)
break
ответ
5475

20.

1
Укажите наименьшее целое значение А, при котором выражение
(xy < 2A) ∨ (x ≥ 11) ∨ (x < 2y)
истинно для любых целых положительных значений x и y.
пояснение
ответ
26

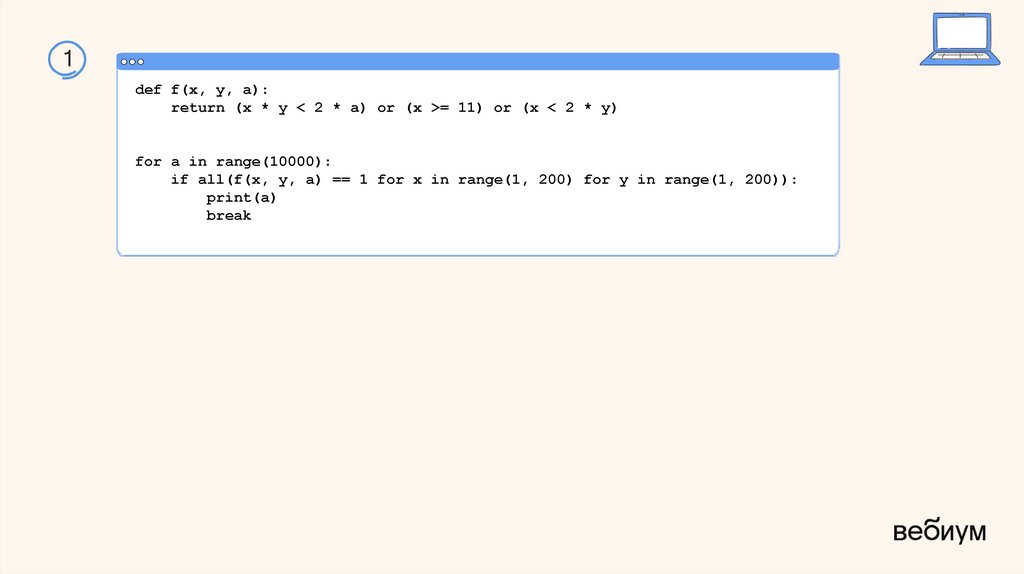
21.

1
def f(x, y, a):
return (x * y < 2 * a) or (x >= 11) or (x < 2 * y)
for a in range(10000):
if all(f(x, y, a) == 1 for x in range(1, 200) for y in range(1, 200)):
print(a)
break

22.

2
Определите наибольшее целое значение A, при котором выражение
(2у + 3х ≠ 135) ∨ (у > А) ∨ (x > A)
истинно для любых целых положительных значений х и у.
пояснение
ответ
26

23.

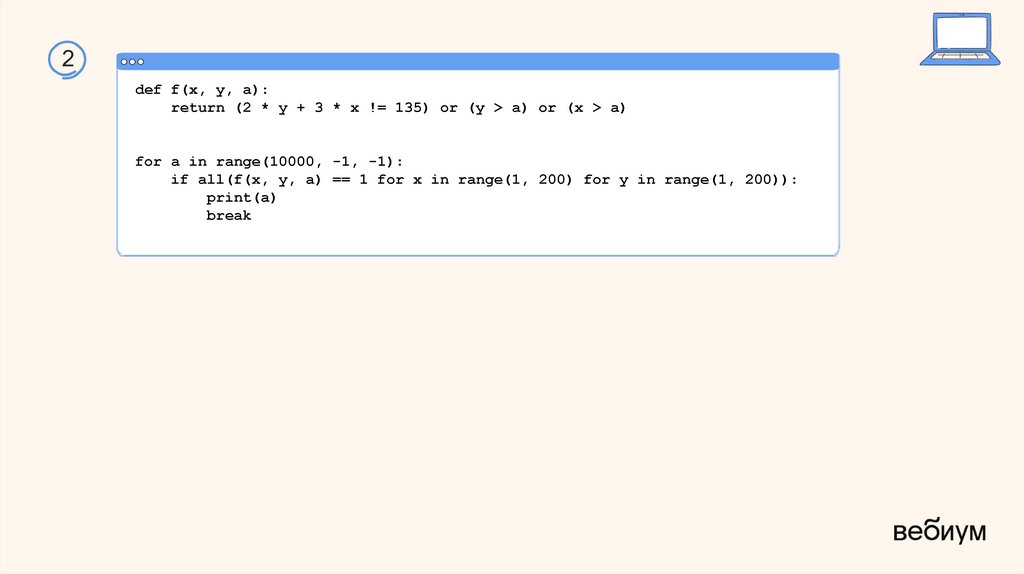
2
def f(x, y, a):
return (2 * y + 3 * x != 135) or (y > a) or (x > a)
for a in range(10000, -1, -1):
if all(f(x, y, a) == 1 for x in range(1, 200) for y in range(1, 200)):
print(a)
break

24.

пошагово разберём задачу на
конъюнкцию
Обозначим через m & n поразрядную
конъюнкцию неотрицательных целых
чисел m и n. Так, например,
14
= 0100 = 4.
2
2 & 5 =2 1110 & 0101
Для какого наименьшего неотрицательного целого числа А формула
((x & 52 ≠ 0) /\ (x & 36 = 0)) → ¬ (x & А = 0)
тождественно истинна (т.е. принимает значение 1) при любом неотрицательном
целом значении переменной х?

25.

1) Создаём функцию от неизвестных переменных и возвращаем выражение из
условия:
def f(x, a):
return ((x & 52 != 0) and (x & 36 == 0)) <= (not (x & a == 0))

26.

2) Перебираем неотрицательные A:
def f(x, a):
return ((x & 52 != 0) and (x & 36 == 0)) <= (not (x & a == 0))
for a in range(1000):

27.

3) Проверяем, что функция истина, при всех неотрицательных
перебираемых x, через конструкцию all:
def f(x, a):
return ((x & 52 != 0) and (x & 36 == 0)) <= (not (x & a == 0))
for a in range(1000):
if all(f(x, a) == 1 for x in range(5000)):

28.

4) Выводим A и прерываем перебор, так как нужно только минимальное
значение:
def f(x, a):
return ((x & 52 != 0) and (x & 36 == 0)) <= (not (x & a == 0))
for a in range(1000):
if all(f(x, a) == 1 for x in range(5000)):
print(a)
break
ответ
16

29.

1
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел
m и n. Так, например, 214&5 =2 1110 2 &0101 = 0100 = 4. Для какого
наименьшего неотрицательного целого числа А формула
x&39 = 0 ∨ (x&11 = 0 → ¬(x&А = 0))
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном
целом значении переменной х)?
пояснение
ответ
36

30.

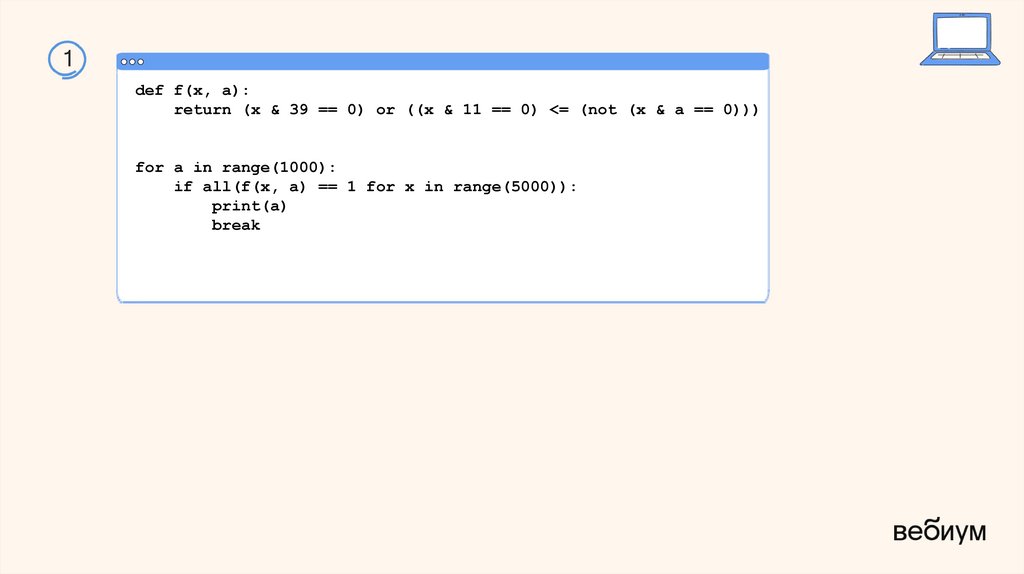
1
def f(x, a):
return (x & 39 == 0) or ((x & 11 == 0) <= (not (x & a == 0)))
for a in range(1000):
if all(f(x, a) == 1 for x in range(5000)):
print(a)
break

31.

2
Введём выражение M&K, обозначающее поразрядную конъюнкцию M и K
(логическое «И» между соответствующими битами двоичной записи).
Определите наибольшее натуральное число A, такое что выражение
(( (X & 13 ≠ 0) ∨ (X & A ≠ 0)) → (X & 13 ≠0)) ∨ ((X & A ≠ 0) ∧ (X & 39 = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном
значении переменной X)?
пояснение
ответ
13

32.

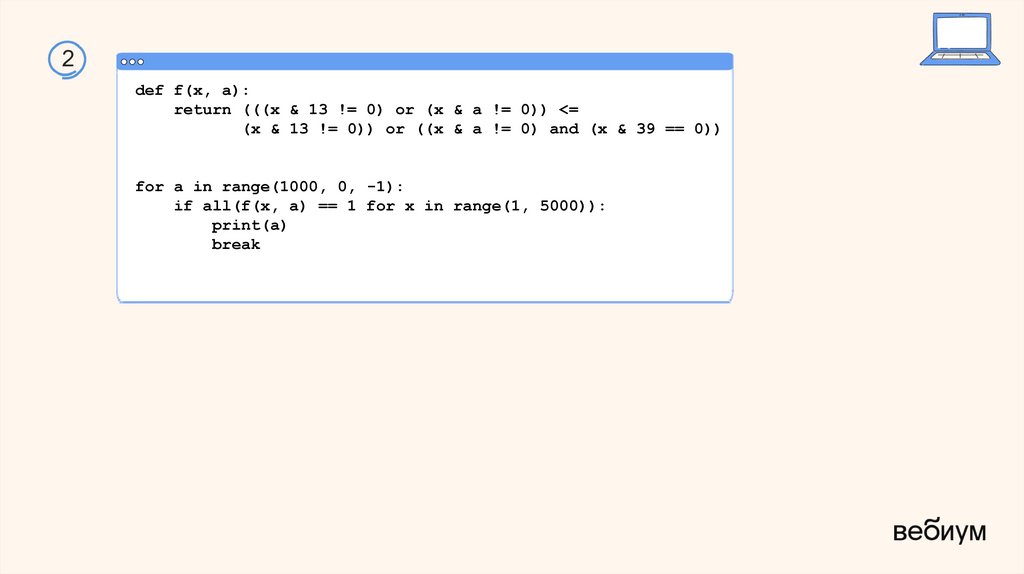
2
def f(x, a):
return (((x & 13 != 0) or (x & a != 0)) <=
(x & 13 != 0)) or ((x & a != 0) and (x & 39 == 0))
for a in range(1000, 0, -1):
if all(f(x, a) == 1 for x in range(1, 5000)):
print(a)
break

33.

пошагово разберём задачу на
Элементами множества Амножества
являются натуральные числа. Известно, что выражение
¬(¬(x ∈ A) ∧ (x ∈ {3, 6, 9, 12})) ∨ ¬(x ∈ {1, 2, 3, 4, 5, 6})
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите
наименьшее возможное количество элементов множества A.

34.

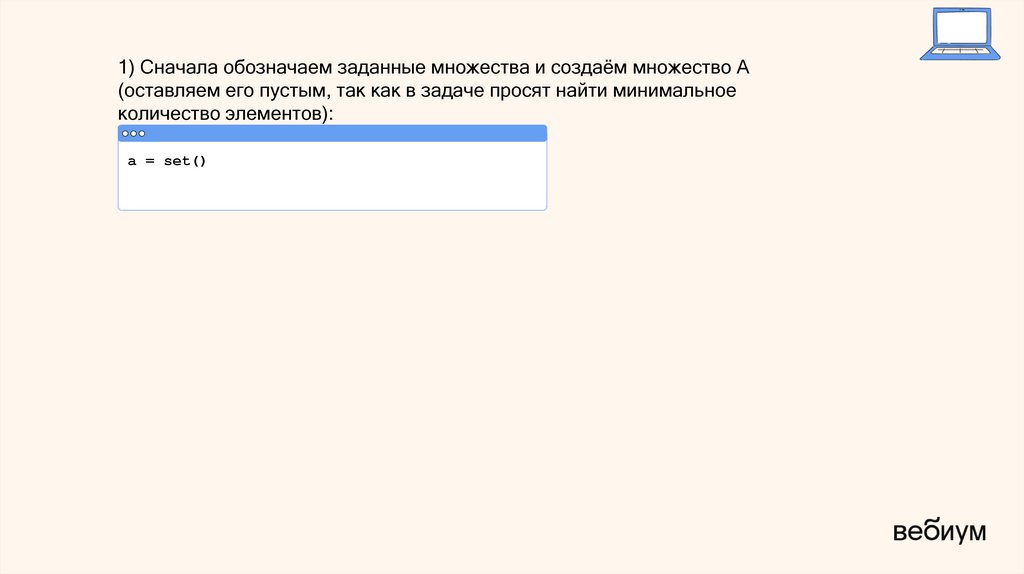
1) Сначала обозначаем заданные множества и создаём множество A
(оставляем его пустым, так как в задаче просят найти минимальное
количество элементов):
a = set()

35.

2) Создаём функцию от x и возвращаем выражение из условия:
a = set()
def f(x):
return (not ((x not in a) and (x in {3, 6, 9, 12}))) or (x not in {1, 2, 3, 4, 5, 6})

36.

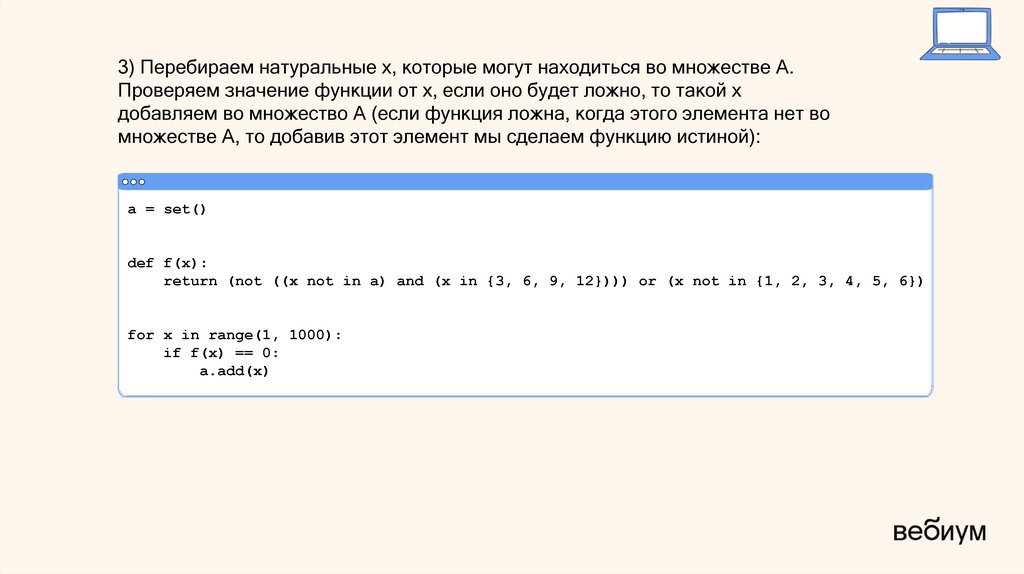
3) Перебираем натуральные x, которые могут находиться во множестве A.
Проверяем значение функции от x, если оно будет ложно, то такой x
добавляем во множество A (если функция ложна, когда этого элемента нет во
множестве А, то добавив этот элемент мы сделаем функцию истиной):
a = set()
def f(x):
return (not ((x not in a) and (x in {3, 6, 9, 12}))) or (x not in {1, 2, 3, 4, 5, 6})
for x in range(1, 1000):
if f(x) == 0:
a.add(x)

37.

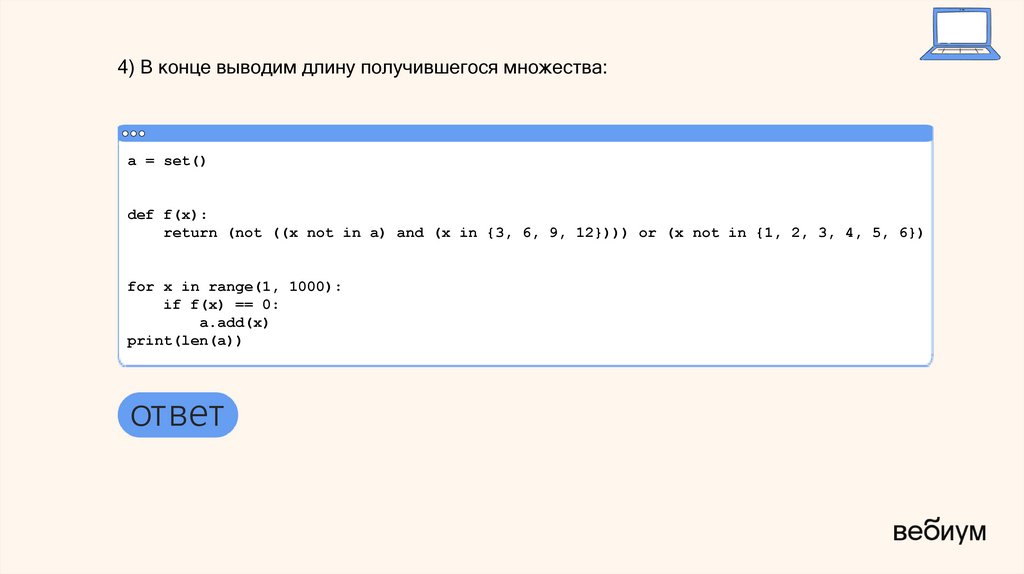
4) В конце выводим длину получившегося множества:
a = set()
def f(x):
return (not ((x not in a) and (x in {3, 6, 9, 12}))) or (x not in {1, 2, 3, 4, 5, 6})
for x in range(1, 1000):
if f(x) == 0:
a.add(x)
print(len(a))
ответ
2

38.

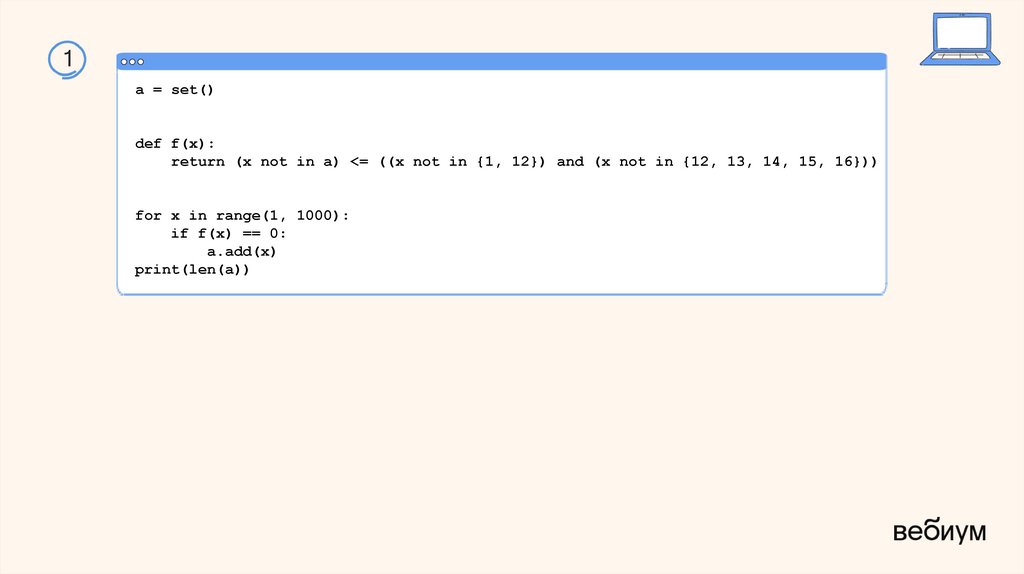
1
Элементами множества А являются натуральные числа. Известно, что
выражение
¬(x ∈ A) → (¬(x ∈ {1, 12}) ∧ ¬(x ∈ {12, 13, 14, 15, 16}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов множества A.
пояснение
6
ответ

39.

1
a = set()
def f(x):
return (x not in a) <= ((x not in {1, 12}) and (x not in {12, 13, 14, 15, 16}))
for x in range(1, 1000):
if f(x) == 0:
a.add(x)
print(len(a))

40.

2
Элементами множеств А, P, Q являются натуральные числа, причём
P={1,3,4,9,11,13,15,17,19,21}, Q={3,6,9,12,15,18,21,24,27,30}. Известно, что
выражение
((x ∈ P) → (x ∈ A)) ∨ ((x ∉ A) → (x ∉ Q))
истинно (т.е. принимает значение 1 при любом значении переменной х.
Определите наименьшее возможное количество элементов в множестве A.
пояснение
ответ
4

41.

2
p = {1, 3, 4, 9, 11, 13, 15, 17, 19, 21}
q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
a = set()
def f(x):
return ((x in p) <= (x in a)) or ((x not in a) <= (x not in q))
for x in range(1, 1000):
if f(x) == 0:
a.add(x)
print(len(a))

42.

пошагово разберём задачу на отрезки
На числовой прямой даны два отрезка: B=[34;72] и C=[32;61]. Укажите
наименьшую возможную длину такого отрезка A, что логическое выражение
((x∈B)→(x∈A))∧(¬(x∈C)∨(x∈A))
истинно (т.е. принимает значение 1) при любом значении переменной x.

43.

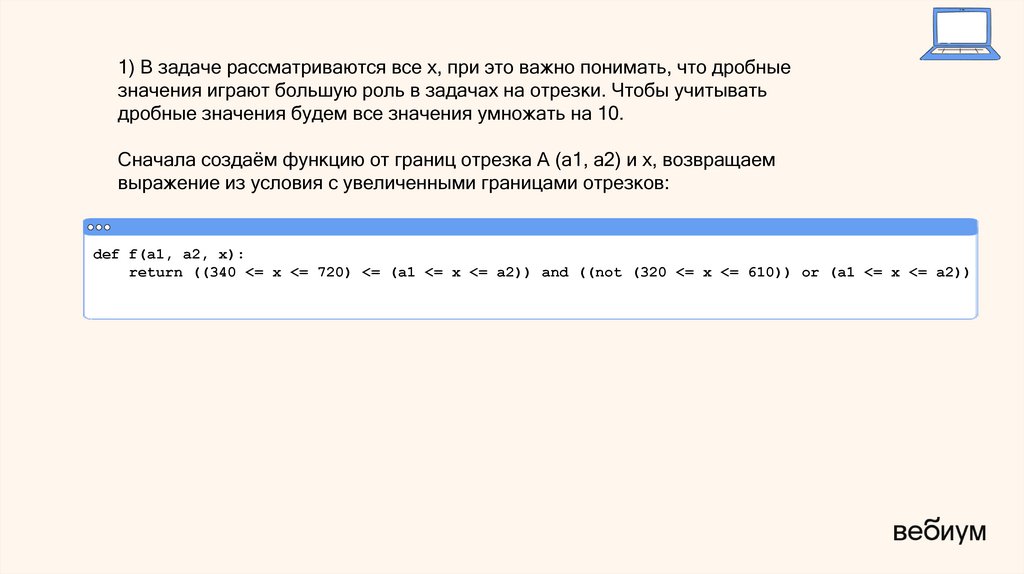
1) В задаче рассматриваются все x, при это важно понимать, что дробные
значения играют большую роль в задачах на отрезки. Чтобы учитывать
дробные значения будем все значения умножать на 10.
Сначала создаём функцию от границ отрезка A (a1, a2) и x, возвращаем
выражение из условия с увеличенными границами отрезков:
def f(a1, a2, x):
return ((340 <= x <= 720) <= (a1 <= x <= a2)) and ((not (320 <= x <= 610)) or (a1 <= x <= a2))

44.

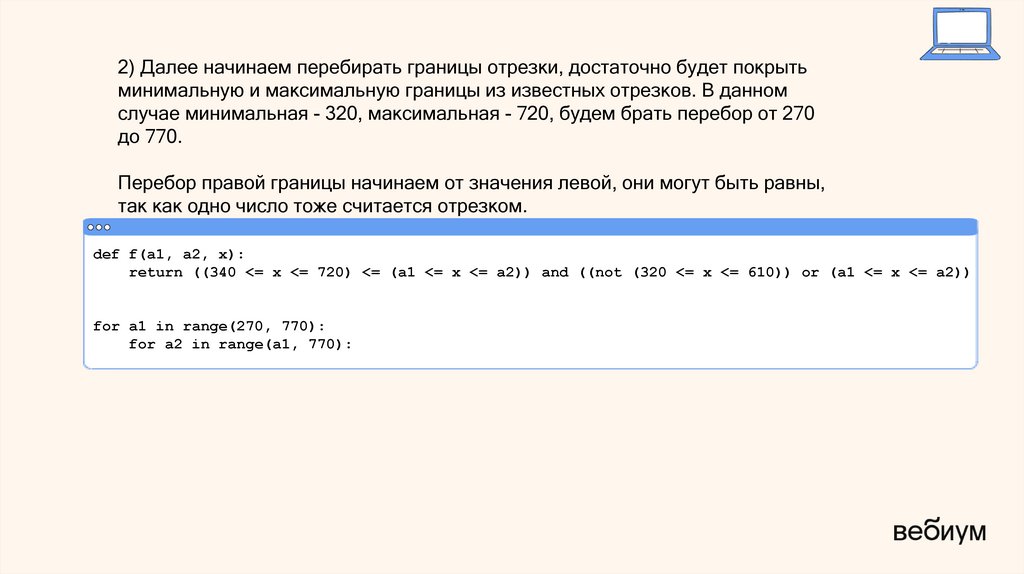
2) Далее начинаем перебирать границы отрезки, достаточно будет покрыть
минимальную и максимальную границы из известных отрезков. В данном
случае минимальная - 320, максимальная - 720, будем брать перебор от 270
до 770.
Перебор правой границы начинаем от значения левой, они могут быть равны,
так как одно число тоже считается отрезком.
def f(a1, a2, x):
return ((340 <= x <= 720) <= (a1 <= x <= a2)) and ((not (320 <= x <= 610)) or (a1 <= x <= a2))
for a1 in range(270, 770):
for a2 in range(a1, 770):

45.

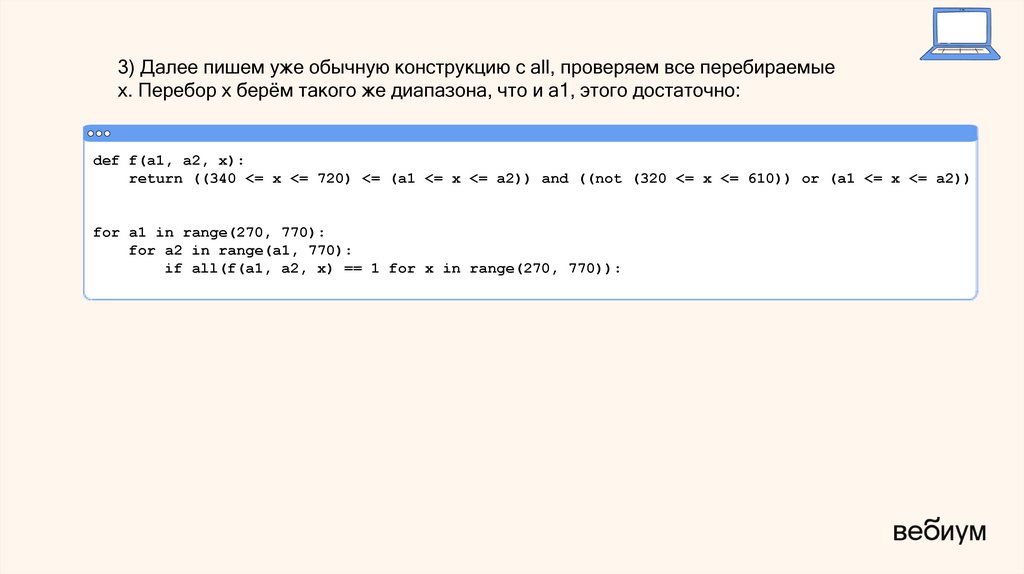
3) Далее пишем уже обычную конструкцию с all, проверяем все перебираемые
x. Перебор x берём такого же диапазона, что и a1, этого достаточно:
def f(a1, a2, x):
return ((340 <= x <= 720) <= (a1 <= x <= a2)) and ((not (320 <= x <= 610)) or (a1 <= x <= a2))
for a1 in range(270, 770):
for a2 in range(a1, 770):
if all(f(a1, a2, x) == 1 for x in range(270, 770)):

46.

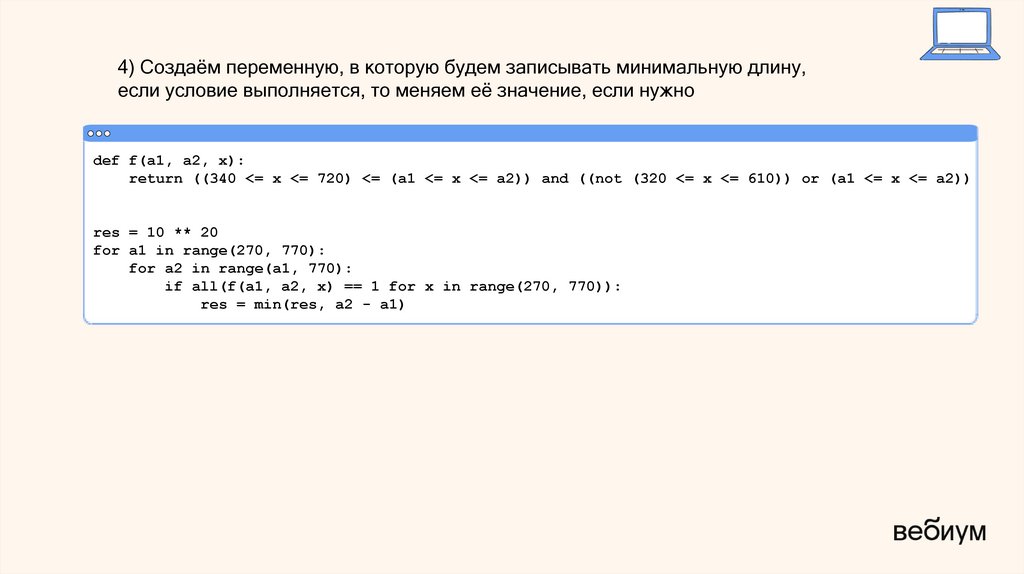
4) Создаём переменную, в которую будем записывать минимальную длину,
если условие выполняется, то меняем её значение, если нужно
def f(a1, a2, x):
return ((340 <= x <= 720) <= (a1 <= x <= a2)) and ((not (320 <= x <= 610)) or (a1 <= x <= a2))
res = 10 ** 20
for a1 in range(270, 770):
for a2 in range(a1, 770):
if all(f(a1, a2, x) == 1 for x in range(270, 770)):
res = min(res, a2 - a1)

47.

5) В конце выводим эту переменную, не забываем делить её на 10:
def f(a1, a2, x):
return ((340 <= x <= 720) <= (a1 <= x <= a2)) and ((not (320 <= x <= 610)) or (a1 <= x <= a2))
res = 10 ** 20
for a1 in range(270, 770):
for a2 in range(a1, 770):
if all(f(a1, a2, x) == 1 for x in range(270, 770)):
res = min(res, a2 - a1)
print(res / 10)
6) Также ответ может получится дробным, например, 23.9, 26.9 и т.д., важно
понимать, что мы всегда округляем в большую сторону.
Дробное значение означает, что у отрезка одна из границ выколотая, но
длина всё равно считается как правая граница - левая граница (длина отрезка
не может быть дробным числом). Пример дробного значения в задаче №2.
ответ
40

48.

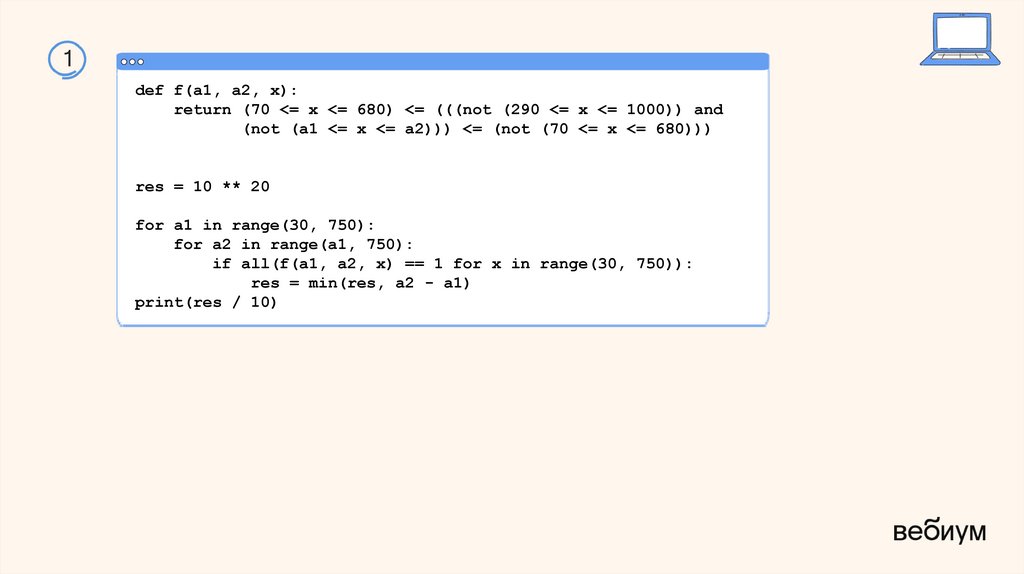
1
На числовой прямой даны два отрезка: D = [7; 68] и C = [29; 100]. Укажите
наименьшую возможную длину такого отрезка A, для которого логическое
выражение
(x∈D)→((¬(x∈C)∧ ¬(x∈A))→ ¬(x∈D))
истинно (т.е. принимает значение 1) при любом значении переменной х.
пояснение
ответ
22

49.

1
def f(a1, a2, x):
return (70 <= x <= 680) <= (((not (290 <= x <= 1000)) and
(not (a1 <= x <= a2))) <= (not (70 <= x <= 680)))
res = 10 ** 20
for a1 in range(30, 750):
for a2 in range(a1, 750):
if all(f(a1, a2, x) == 1 for x in range(30, 750)):
res = min(res, a2 - a1)
print(res / 10)

50.

2
Заданы два отрезка P = [6, 17] и Q = [13, 28], лежащие на числовой прямой.
Также существует отрезок А. Он таков, что формула
((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)
истинна, причем переменная x может принимать любые значения. Какую
наибольшую длину может принимать отрезок А? Определите и запишите в ответ
целое число.
пояснение
ответ
22

51.

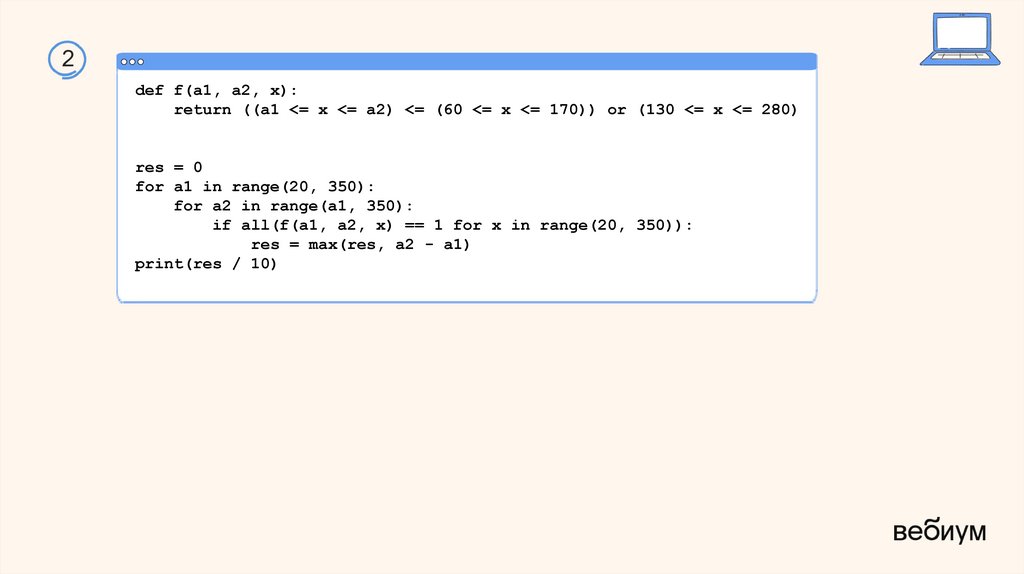
2
def f(a1, a2, x):
return ((a1 <= x <= a2) <= (60 <= x <= 170)) or (130 <= x <= 280)
res = 0
for a1 in range(20, 350):
for a2 in range(a1, 350):
if all(f(a1, a2, x) == 1 for x in range(20, 350)):
res = max(res, a2 - a1)
print(res / 10)

52.

1
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без
остатка на натуральное число m».
Пусть на числовой прямой дан отрезок B = [120; 130].
Для какого наименьшего натурального числа А формула
((x∈B)→¬ДЕЛ(x,7))∨(A>2x)
истинна (т.е. принимает значение 1) при любом натуральном значении
переменной x?
пояснение
253
ответ

53.

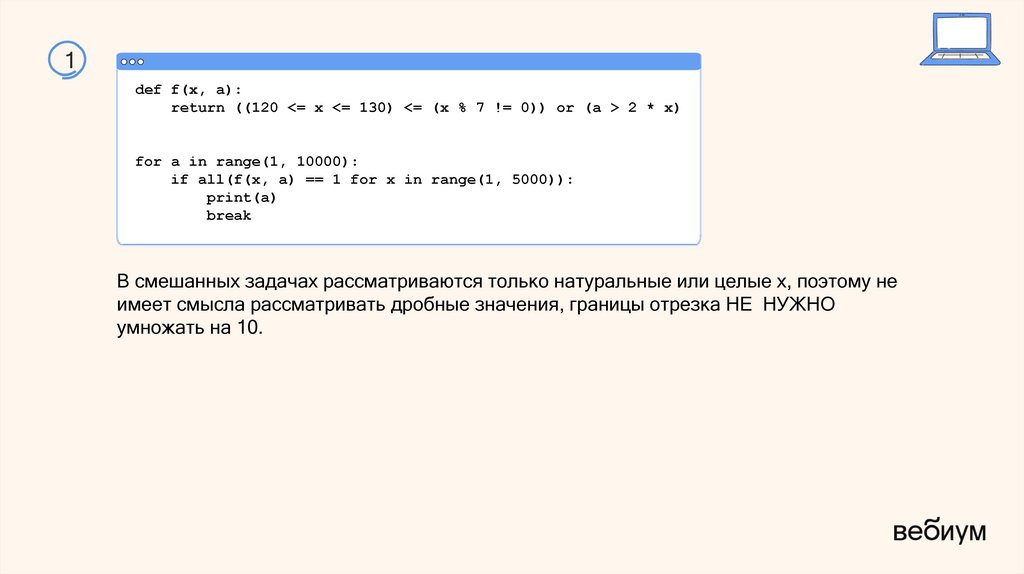
1
def f(x, a):
return ((120 <= x <= 130) <= (x % 7 != 0)) or (a > 2 * x)
for a in range(1, 10000):
if all(f(x, a) == 1 for x in range(1, 5000)):
print(a)
break
В смешанных задачах рассматриваются только натуральные или целые x, поэтому не
имеет смысла рассматривать дробные значения, границы отрезка НЕ НУЖНО
умножать на 10.

54.

2
Обозначим через ДЕЛ(n,m) утверждение «натуральное число n делится без
остатка на натуральное число m». Пусть на числовой прямой дан отрезок
B∈[80,100]. Для какого наибольшего натурального числа А формула
ДЕЛ(x,17)→(¬(x∈B)∨(A<x+30))
тождественно истинна (т.е. принимает значение 1) при любом натуральном
значении переменной х?
пояснение
114
ответ

55.

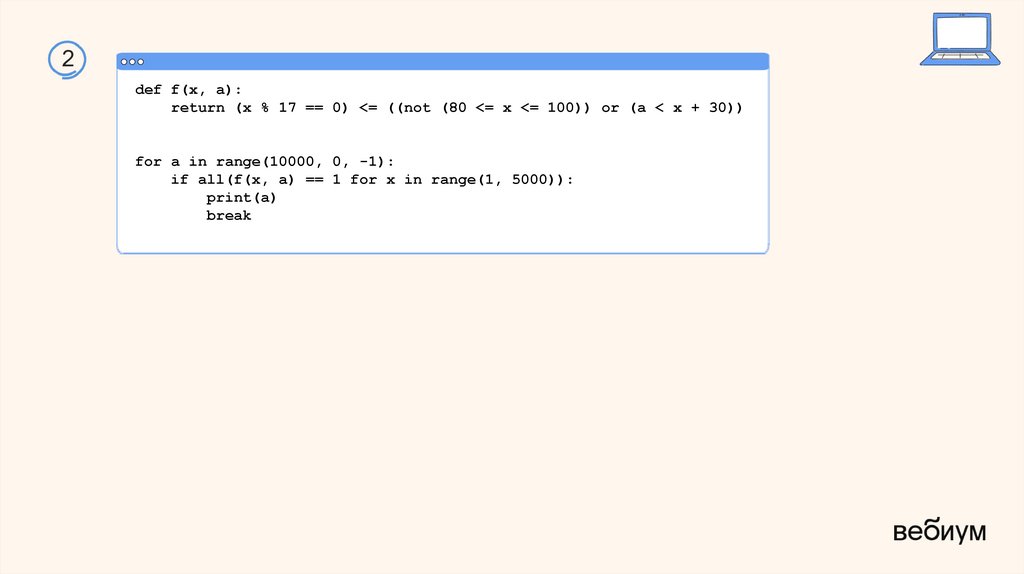
2
def f(x, a):
return (x % 17 == 0) <= ((not (80 <= x <= 100)) or (a < x + 30))
for a in range(10000, 0, -1):
if all(f(x, a) == 1 for x in range(1, 5000)):
print(a)
break