Похожие презентации:
Решение задач линейного программирования
1.
Лабораторная работа № 1Решение задач линейного
программирования
2.
Цель:Целью лабораторной работы является приобретение
студентами практических навыков решения задач
линейного программирования графическим методом и
использования инструмента Поиск решения среды
Microsoft Ехсеl для нахождения оптимального допустимого
решения.
3.
Содержание:1. Решение задачи линейного программирования
геометрическим методом.
2. Решение задачи линейного программирования с
применением среды Microsoft Ехсеl.
3. Разработка словестной формулировки условия для
задачи линейного программирования.
4.
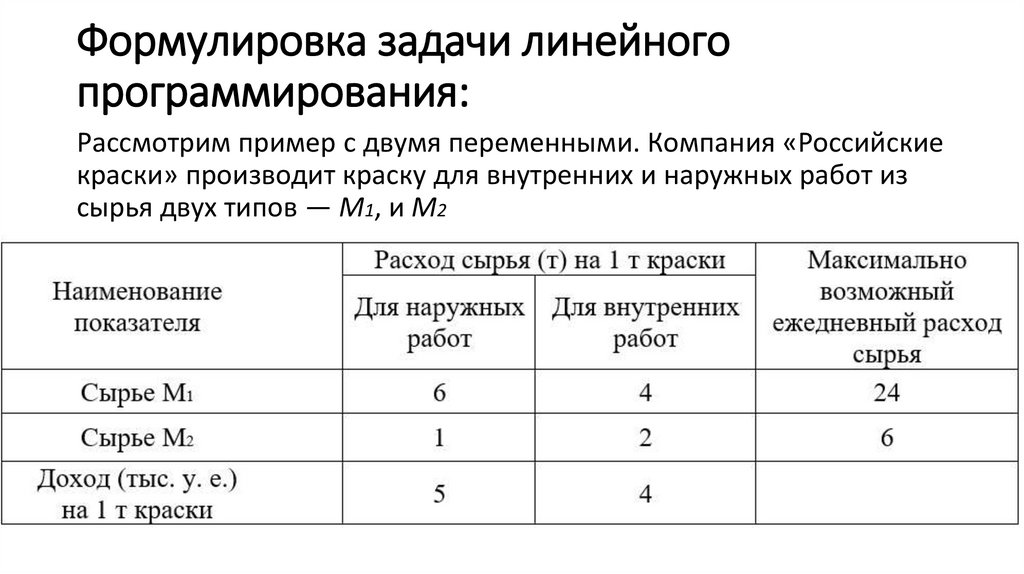
Формулировка задачи линейногопрограммирования:
Рассмотрим пример с двумя переменными. Компания «Российские
краски» производит краску для внутренних и наружных работ из
сырья двух типов — М1, и М2
5.
Отдел маркетинга компании ограничил ежедневноепроизводство краски для внутренних работ до 2 т, а также
поставил условие, чтобы этот вид продукции на превышал
более чем на 1 т аналогичный показатель производства
краски для внешних работ. Компания хочет определить
оптимальное соотношение между видами выпускаемой
продукции для максимизации общего ежедневного
дохода.
6.
Математическая модель задачи линейногопрограммирования
Задача линейного программирования, как и любая задача
исследования операций, включает три основных элемента.
1. Переменные, которые следует определить
2. Целевая функция, подлежащая оптимизации
3. Ограничения, которым должны удовлетворять переменные
7.
В нашем примере необходимо определить ежедневныеобъемы производства краски для внутренних и наружных
работ. Обозначим их как переменные модели: х1 ежедневный объем производства краски для наружных
работ; х2 - ежедневный объем производства краски для
внутренних работ.
Используя эти переменные, строим целевую функцию Z,
отражающую полученные суммарного ежедневного дохода
компании, который необходимо максимизировать:
8.
Ограничения на сырье можно записать следующимобразом:
Используемый объем сырья для производства обоих видов
краски меньше или равно максимально возможный
ежедневный расход сырья
Из таблицы с данными получим используемые объемы (т):
1. Для сырья М1:
6 ∙












 Программирование
Программирование








