Описание структуры и свойств радиоматериалов (элементы кристаллофизики)

1.

2
Тема 1.
Описание структуры и свойств радиоматериалов
(элементы кристаллофизики)
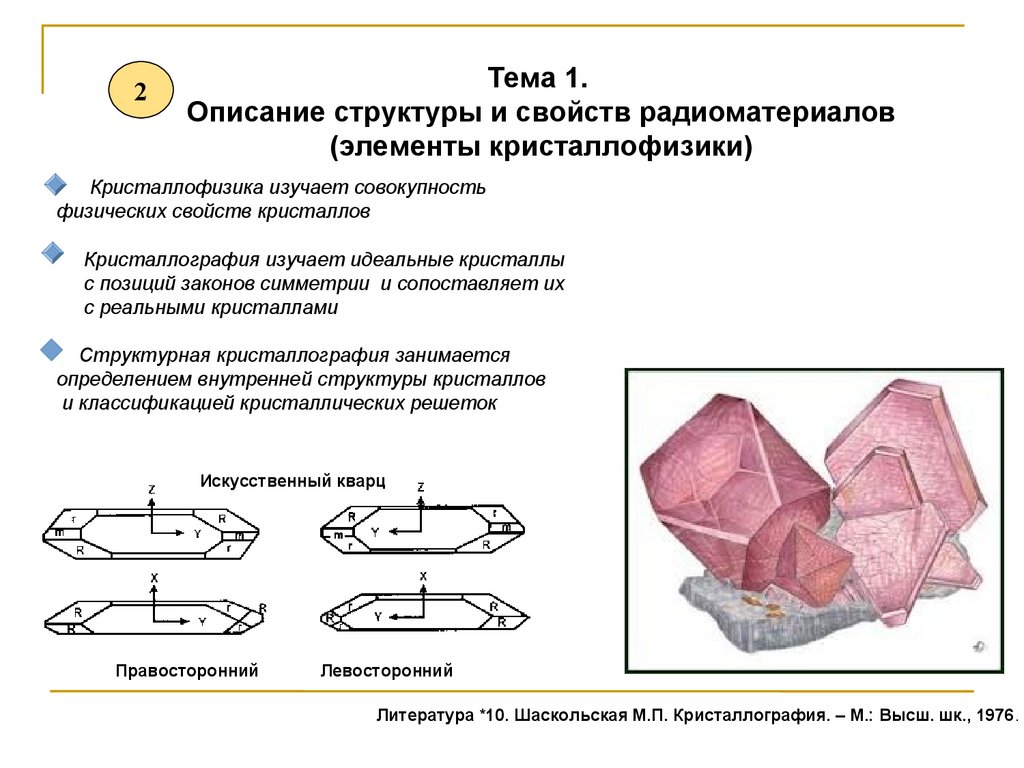
Кристаллофизика изучает совокупность
физических свойств кристаллов
Кристаллография изучает идеальные кристаллы
c позиций законов симметрии и сопоставляет их
с реальными кристаллами
Структурная кристаллография занимается
определением внутренней структуры кристаллов
и классификацией кристаллических решеток
Искусственный кварц
Правосторонний
Левосторонний
Литература *10. Шаскольская М.П. Кристаллография. – М.: Высш. шк., 1976.

2.

Радиотехнические материалы (радиоматериалы) Это: класс материалов, характеризуемых определёнными свойствами по отношению к
электромагнитному полю и применяемых в радиотехнике с учётом этих свойств.
Радиоматериалы необходимы для изготовления проводов, кабелей, волноводов, антенн,
изоляторов, конденсаторов, резисторов, катушек индуктивности, трансформаторов, постоянных
магнитов, полупроводни ковых приборов, электронных ламп, устройств функциональной
электроники.
От свойств радиоматериалов зависит работа электрической схемы радиотехнического устройства.
Основными физическими параметрами радиоматериалов являются: электропроводность,
диэлектрическая и магнитная проницаемость.
По физическим (электрическим и магнитным) свойствам все радиоматериалы принято
подразделять на 4 класса.
По электрическим свойствам выделяют проводниковые, диэлектрические и полупроводниковые
материалы, а по магнитным - магнитные и немагнитные материалы.
В зависимости от области частот, в которой работают радиоматериалы, их подразделяют на
низкочастотные и высокочастотные.
Низкочастотные материалы предназначаются для работы при постоянном токе и в области
звуковых частот, до 10-20 кГц.
Высокочастотные материалы рассчитаны на работу при частотах выше 10-20 кГц
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

3.

Блок связей основных понятий и определений
• кристаллическое (дальний порядок),
Твердое тело –
• аморфное
(ближний порядок)
1) кристалл
2)
3)
10) Физические свойства
кристаллов
ПКР + базис (атомы, молекулы)
Элементарная ячейка
5) Решетки Браве
14 типов
+
4) Трансляция
11)
Принципы
кристаллофизики
6)
ячейка
Вигнера-Зейтца
12)
7)
Предельные
группы Кюри
Класс симметрии
Точечная группа
8)
Симметрия
Конечных многогранников
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
9)
Матрицы
Элементов симметрии
13) Тензоры
физических
свойств

4.

1) Кристалл —анизотропное трехмерное упорядоченное твердое тело, находящееся в
термодинамическом равновесии с окружающей средой
Криста́ ллы (от греч. κρύσταλλος первоначально «лёд») — твёрдые тела, в которых атомы расположены
закономерно, образуя трёхмерно-периодическую пространственную укладку — кристаллическую решётку.
Кристаллы — это твёрдые вещества, имеющие естественную внешнюю форму правильных симметричных
многогранников, основанную на их внутренней структуре, то есть на одном из нескольких определённых
регулярных расположений составляющих вещество частиц (атомов, молекул, ионов).
Современное определение кристалла дано Международным союзом кристаллографов
(http://reference.iucr.org/dictionary/Crystal):
Материал представляет собой кристалл, если он имеет преимущественно острую дифракционную картину
Электронограмма
поликристалла
Электронограмма
текстуры
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
Электронограмма
монокристалла

5.

идеальные
кристаллы
Строение атома
Тип химической связи
Строение Кристалла
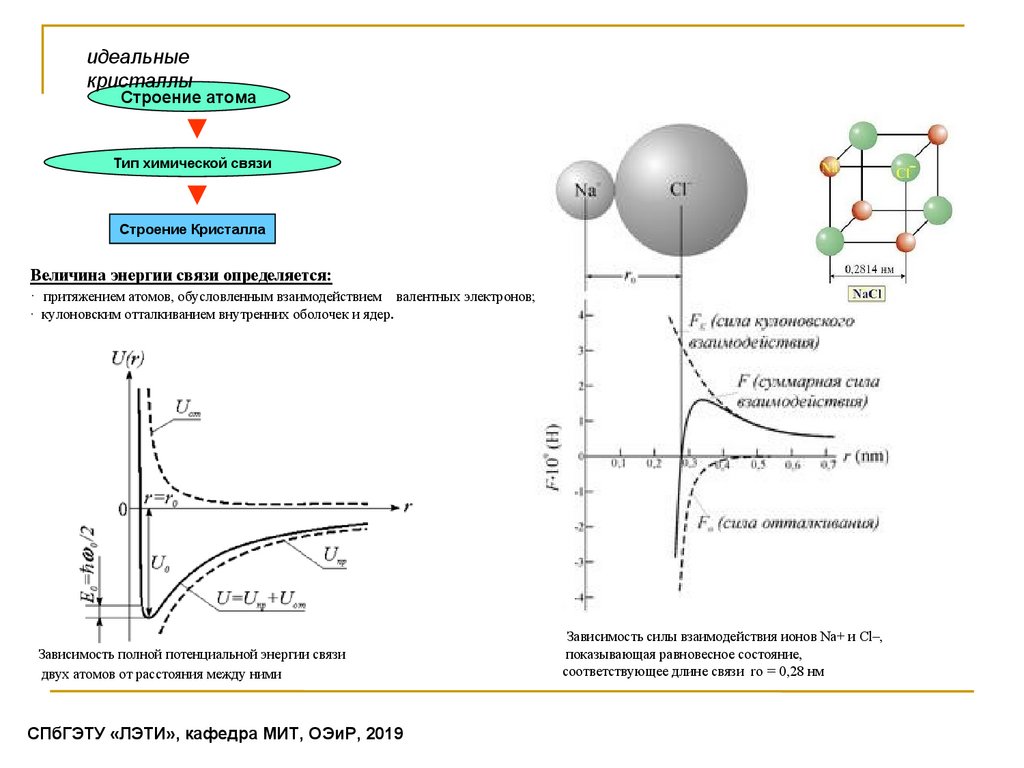
Величина энергии связи определяется:
· притяжением атомов, обусловленным взаимодействием валентных электронов;
· кулоновским отталкиванием внутренних оболочек и ядер.
Зависимость полной потенциальной энергии связи
двух атомов от расстояния между ними
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
Зависимость силы взаимодействия ионов Na+ и Cl–,
показывающая равновесное состояние,
соответствующее длине связи ro = 0,28 нм

6.

Значения энергий химической связи для некоторых элементов,
эВ/ат
He
H
4,48
Li
1,65
Be
3,33
B
5,81
C
7,36
N
−
O
−
F
−
Ne
0,02
Na
1,13
Mg
1,53
Al
3,34
Si
4,64
P
−
S
2,86
Cl
Ar
0,08
K
0,941
Ca
1,825
Sc
3,93
Ti
4,855
V
5,30
Cr
4,10
Mn
2,98
Fe
2,29
Co
4,387
Ni
4,435
Cu
3,50
Zn
1,35
Ga
2,78
Ge
3,87
As
3,0
Se
2,13
Br
1,22
Kr
0,116
Rb
0,858
Sr
−
Y
4,387
Zr
6,316
Nb
7,47
Mo
6,81
Tc
−
Ru
6,615
Rh
5,752
Pd
3,936
Ag
2,96
Cd
1,16
In
2,60
Sn
3,12
Sb
2,70
Te
2,6
−
−
Cs
0,827
Ba
1,86
La
4,491
Hf
6,35
Ta
8,089
W
8,66
Re
8,10
Os
−
Ir
6,93
Pt
5,852
Au
3,78
Hg
0,694
Tl
1,87
Pb
2,04
Bi
2,15
−
−
−
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

7.

:
Кристаллическая структура — это расположение частиц (атомов, молекул, ионов) в кристалле.
Будучи индивидуальной для каждого вещества, кристаллическая структура относится к основным
физико-химическим свойствам этого вещества.
Кристаллическую структуру с трёхмерной периодичностью называют кристаллической решёткой[
2) Кристаллическая структура может быть, представлена в виде кристаллической пространственной
решетки ( КР), заполненной базисом (одним атомом или совокупностью атомов).
Кристаллическая решетка— вспомогательный геометрический образ, вводимый для анализа строения
кристалла.
КР – математическая (геометрическая) абстракция, способ представления периодически
повторяющихся в пространстве отдельных атомов (совокупности атомов).
,
3) Элементарная ячейка КР может быть построена на элементарных трансляциях
(базисных векторах) a, b, c,
так что все точки определяются радиус вектором r=n 1 a+n 2 b+n 3 c, где
n 1 ,n 2 ,n 3 – произвольные целые числа
.
В зависимости от соотношения модулей базисных векторов, углов
между ними и положения узлов, все элементарные ячейки
классифицируют по Браве.
По соотношению между базисными векторами и углами, элементарные
ячейки подразделяются
на три категории: высшую, среднюю и низшую, и 7 сингоний:
-Кубическая a= b= c , α=β=γ=90 град,
-Тетрагональная a= b≠ c , α=β=γ=90 град,
-Ромбическая a ≠ b ≠ c , α=β=γ=90 град,
-Гексагональная a= b≠ c , α=β=90 град, γ=60 град,
-Ромбоэдрическая (тригональная)
-Моноклинная a ≠ b ≠ c , α=β=90 град, γ-любой,
-Триклинная a ≠ b ≠ c , α,β,γ -любые
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

8.

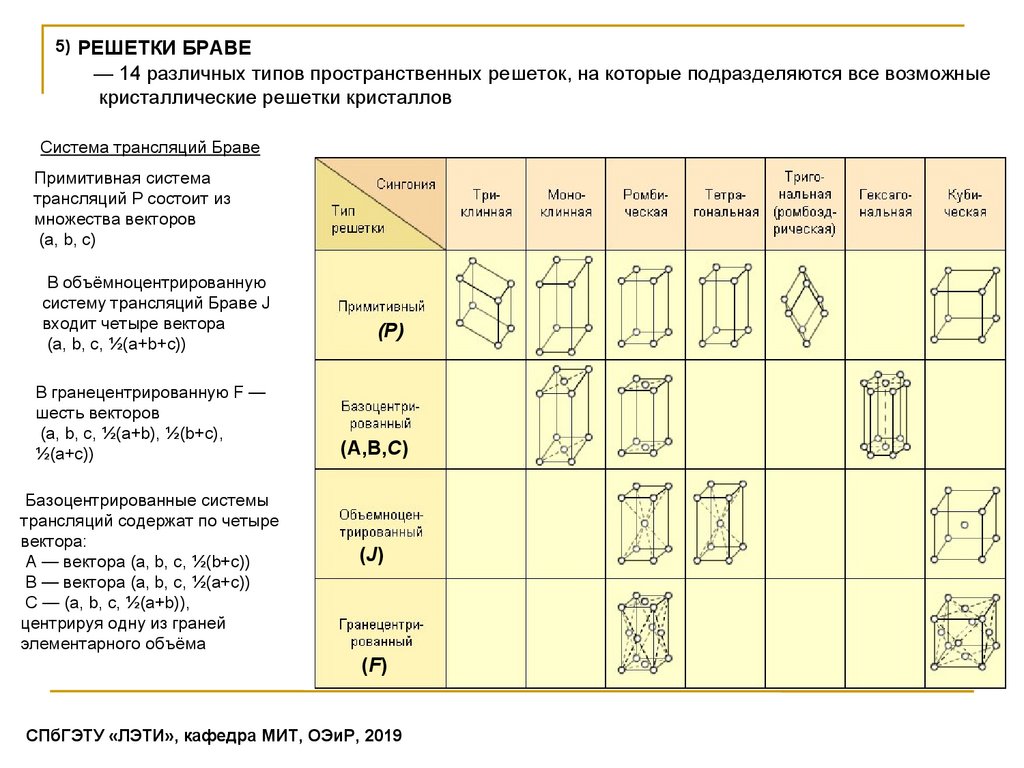
5) РЕШЕТКИ БРАВЕ
— 14 различных типов пространственных решеток, на которые подразделяются все возможные
кристаллические решетки кристаллов
Система трансляций Браве
Примитивная система
трансляций P состоит из
множества векторов
(a, b, c)
В объёмноцентрированную
систему трансляций Браве J
входит четыре вектора
(a, b, c, ½(a+b+c))
В гранецентрированную F —
шесть векторов
(a, b, c, ½(a+b), ½(b+c),
½(a+c))
Базоцентрированные системы
трансляций содержат по четыре
вектора:
A — вектора (a, b, c, ½(b+c))
B — вектора (a, b, c, ½(a+c))
C — (a, b, c, ½(a+b)),
центрируя одну из граней
элементарного объёма
(P)
(A,B,C)
(J)
(F)
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

9.

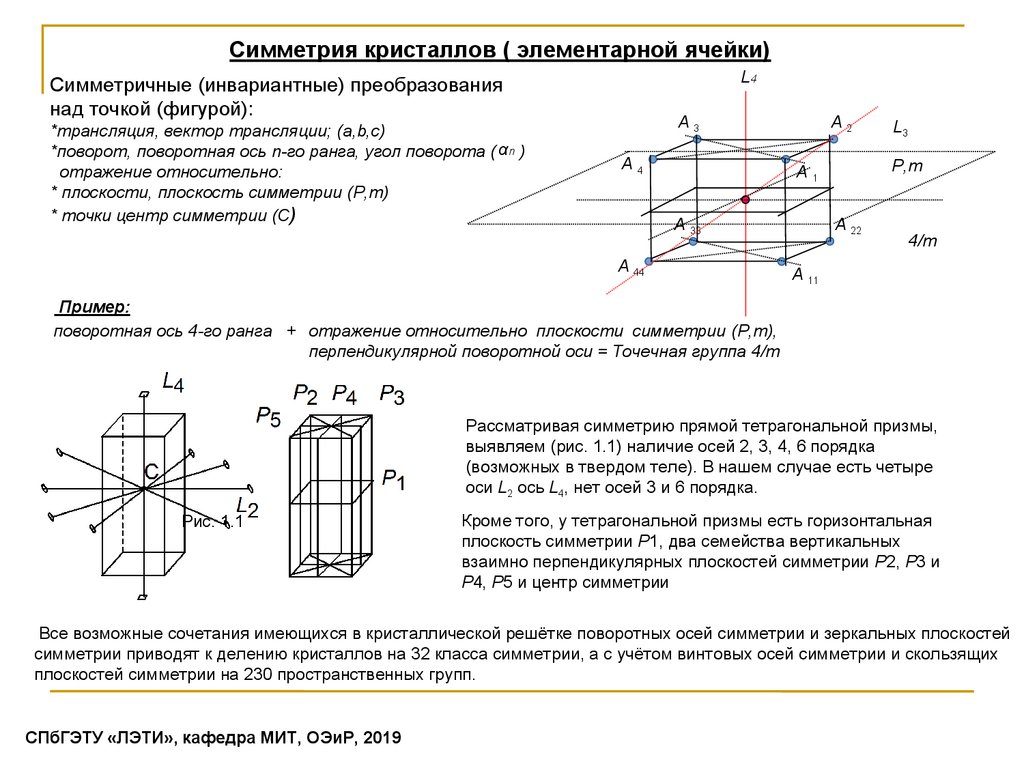
Cимметрия кристаллов ( элементарной ячейки)
L4
Симметричные (инвариантные) преобразования
над точкой (фигурой):
*трансляция, вектор трансляции; (a,b,c)
*поворот, поворотная ось n-го ранга, угол поворота ( αn )
отражение относительно:
* плоскости, плоскость симметрии (P,m)
* точки центр симметрии (C)
А3
А4
А2
P,m
А1
А 33
А 44
L3
А 22
4/m
А 11
Пример:
поворотная ось 4-го ранга + отражение относительно плоскости симметрии (P,m),
перпендикулярной поворотной оси = Точечная группа 4/m
Рассматривая симметрию прямой тетрагональной призмы,
выявляем (рис. 1.1) наличие осей 2, 3, 4, 6 порядка
(возможных в твердом теле). В нашем случае есть четыре
оси L2 ось L4, нет осей 3 и 6 порядка.
Рис. 1.1
Кроме того, у тетрагональной призмы есть горизонтальная
плоскость симметрии P1, два семейства вертикальных
взаимно перпендикулярных плоскостей симметрии P2, P3 и
P4, P5 и центр симметрии
Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей
симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих
плоскостей симметрии на 230 пространственных групп.
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

10.

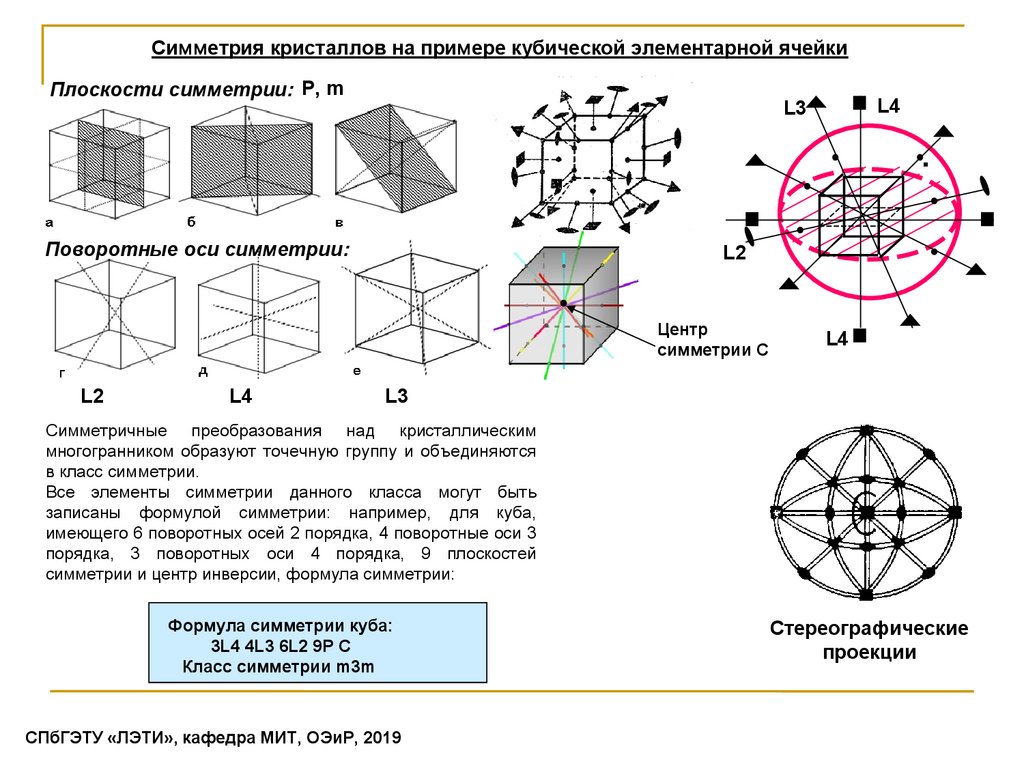
Cимметрия кристаллов на примере кубической элементарной ячейки
Плоскости симметрии: P, m
L4
L3
.
Поворотные оси симметрии:
L2
Центр
симметрии С
L2
L4
L4
L3
Симметричные преобразования над кристаллическим
многогранником образуют точечную группу и объединяются
в класс симметрии.
Все элементы симметрии данного класса могут быть
записаны формулой симметрии: например, для куба,
имеющего 6 поворотных осей 2 порядка, 4 поворотные оси 3
порядка, 3 поворотных оси 4 порядка, 9 плоскостей
симметрии и центр инверсии, формула симметрии:
Формула симметрии куба:
3L4 4L3 6L2 9P C
Класс симметрии m3m
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
Стереографические
проекции

11.

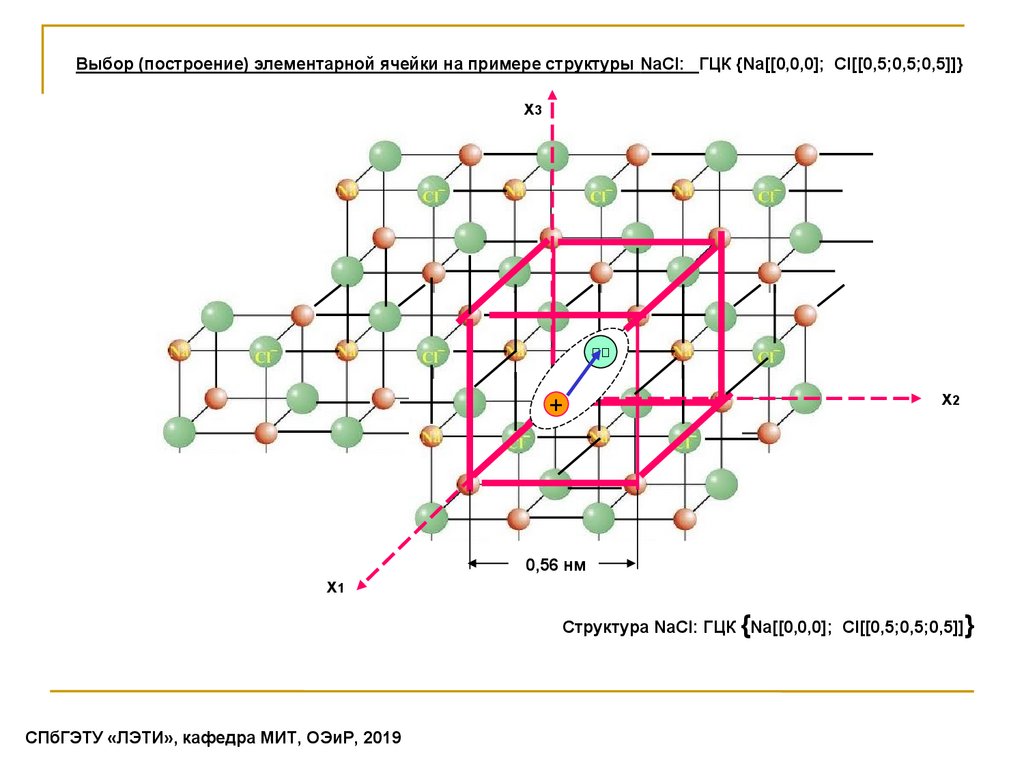
Выбор (построение) элементарной ячейки на примере структуры NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}
x3

+
x2
0,56 нм
x1
Структура NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

12.

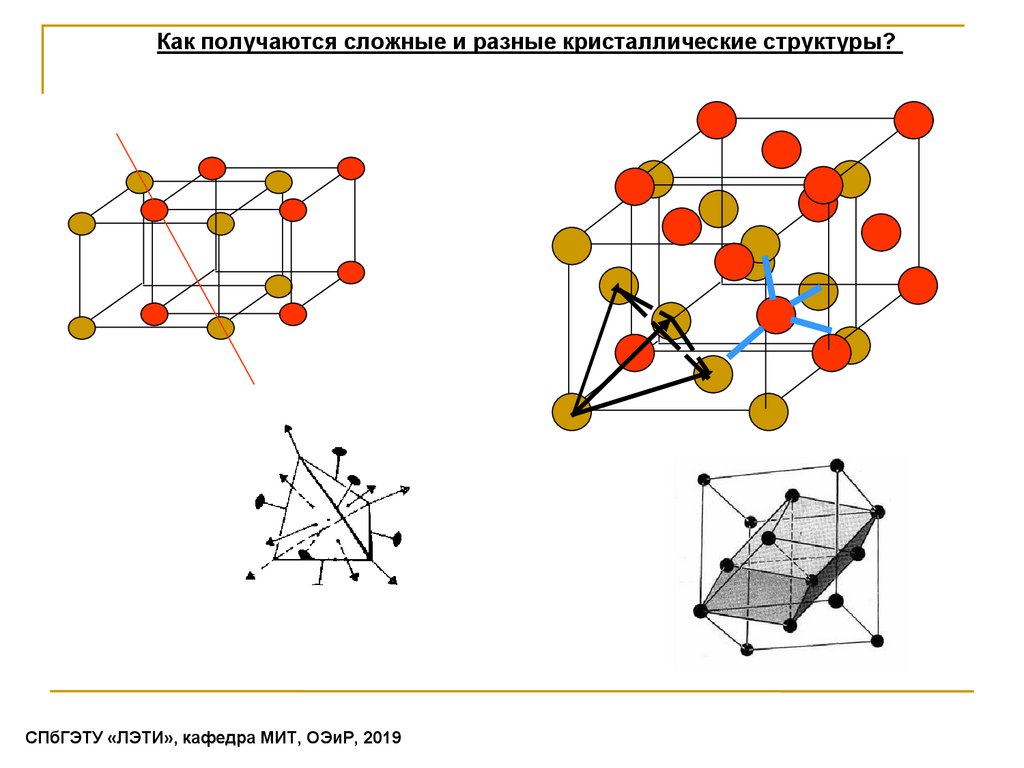
Как получаются сложные и разные кристаллические структуры?
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

13.

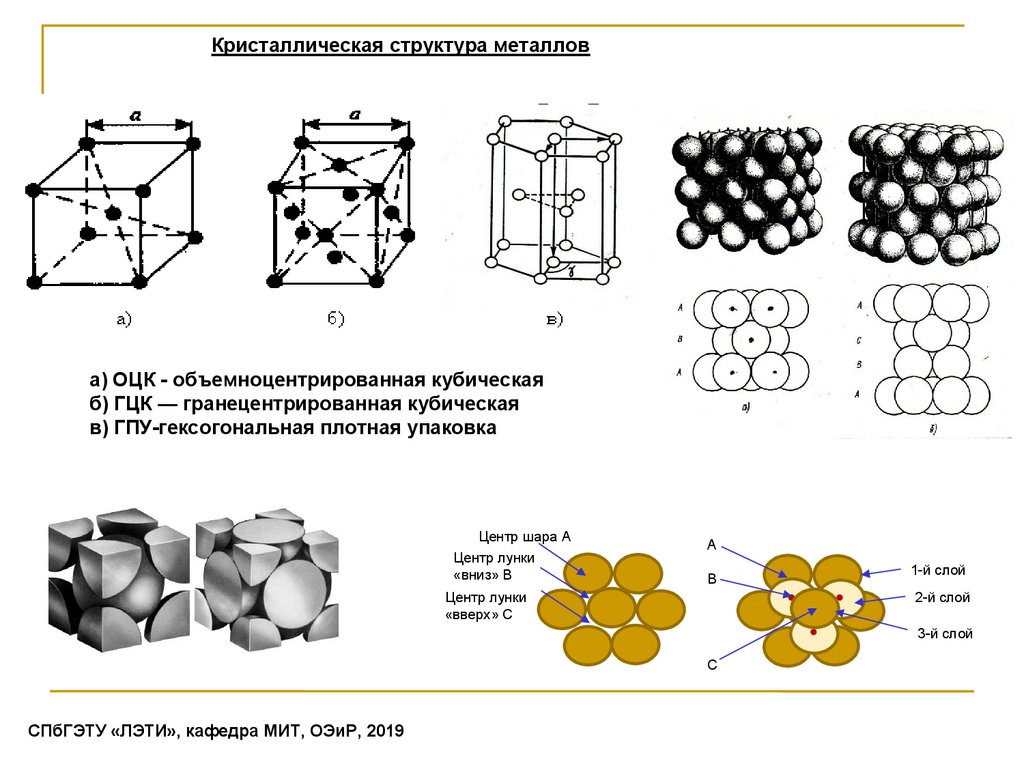
Кристаллическая структура металлов
а) ОЦК - объемноцентрированная кубическая
б) ГЦК — гранецентрированная кубическая
в) ГПУ-гексогональная плотная упаковка
Центр шара А
Центр лунки
«вниз» В
А
В
Центр лунки
«вверх» С
1-й слой
2-й слой
3-й слой
С
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

14.

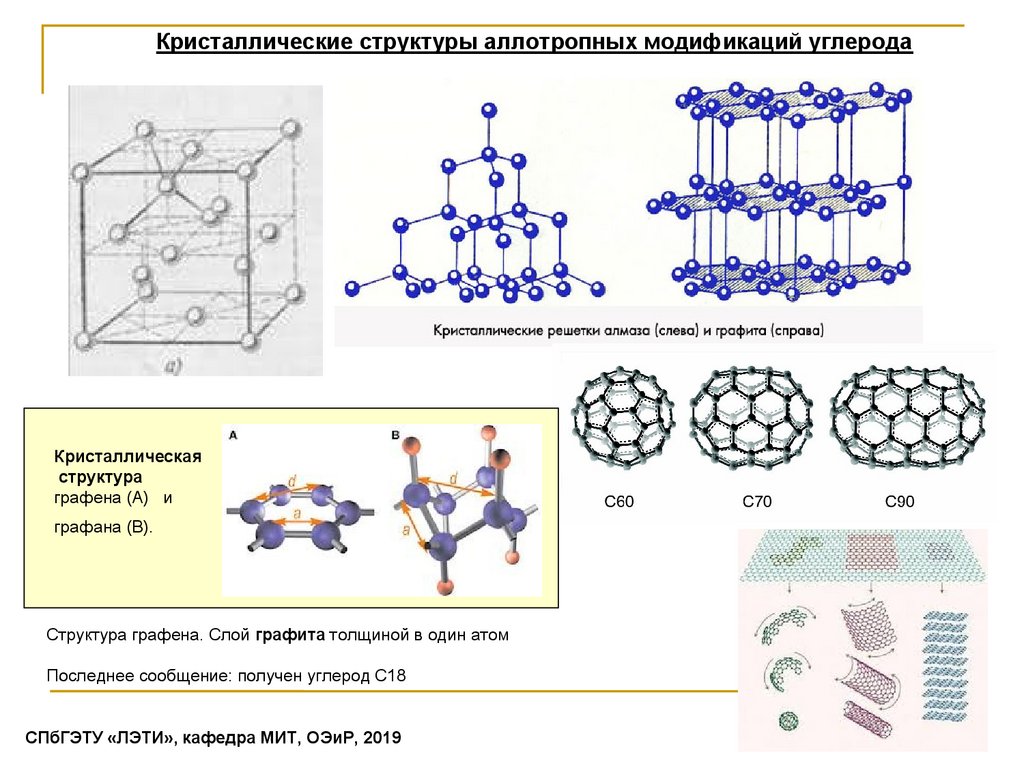
Кристаллические структуры аллотропных модификаций углерода
Кристаллическая
структура
графена (A) и
графана (B).
Структура графена. Слой графита толщиной в один атом
Последнее сообщение: получен углерод С18
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

15.

BaTiO2- титанат вария, сегнетоэлектрик
Кристаллическая структура
YBa2 Cu3 O7
Природный кварц - SiO2
Сапфир – Al2O3
Si
–O
– Cu
– Ba
–Y
Высокотемпературный
сверхпроводник
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
Монокристалл кремния,
выращенный по методу
Чохральского

16.

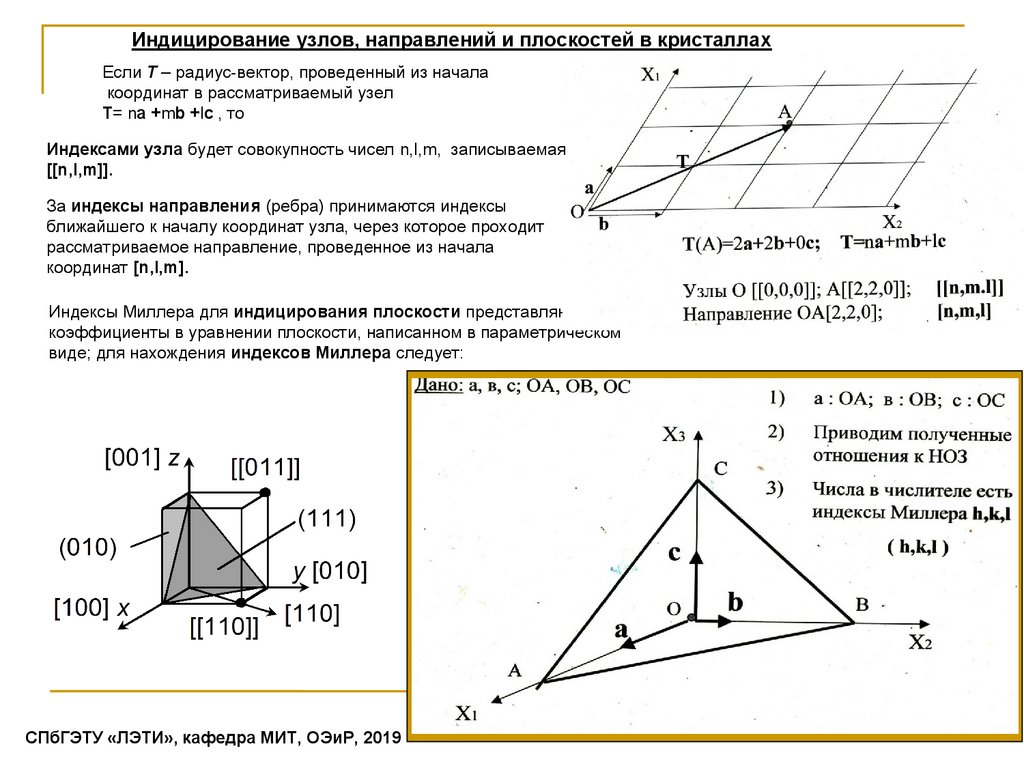
Индицирование узлов, направлений и плоскостей в кристаллах
Если Т – радиус-вектор, проведенный из начала
координат в рассматриваемый узел
T= na +mb +lc , то
Индексами узла будет совокупность чисел n,l,m, записываемая
[[n,l,m]].
За индексы направления (ребра) принимаются индексы
ближайшего к началу координат узла, через которое проходит
рассматриваемое направление, проведенное из начала
координат [n,l,m].
Индексы Миллера для индицирования плоскости представляют собой
коэффициенты в уравнении плоскости, написанном в параметрическом
виде; для нахождения индексов Миллера следует:
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

17.

Матрицы элементов симметрии
Преобразования симметрии в кристаллическом пространстве описываются
как соответствующие преобразования координат (рис.1.3).
Точка с координатами x, y, z после преобразования симметрии займет новое
положение с координатами x’, y’, z’, определяющимися уравнениями
преобразования:
x c11 x c12 y c13 z,
y c 21x c 22 y c 23 z,
z c31x c32 y c33 z,
где ci, j – косинусы углов между
осями координат i, j = 1, 2, 3.
Любому преобразованию симметрии можно поставить
в соответствие матрицу преобразования Δ i, j , элементами которой являются косинусы углов
c11 c12 c13
Δ i , j c 21 c 22 c 23 .
c
31 c 32 c 33
c i, j
Задача 1.3. Записать матричное представление оси второго порядка,
параллельно оси Z.
Требуемое симметричное преобразование представляет поворот кристаллографических координат вокруг оси L2
: связанную с исходной x, y, z
(оси Z) на угол 180°. Введем новую систему координат x’, y’, z’,
x cos( xx ) x cos( ) x ( 1) x ,
следующими соотноше­ниями:
y cos( yy ) y cos( ) y ( 1) y ,
z cos( zz ) z cos(0) z ( 1) z.
Соотношения между разноименными осями (например xy’) определяются косинусами углов равных 90° (все
разноименные оси взаимно перпендикулярны), поэтому искомое преобразование симметрии следует записать в
1 0 0
виде матрицы:
Δ(L2 || Z ) 0 1
0 0
0 .
1

18.

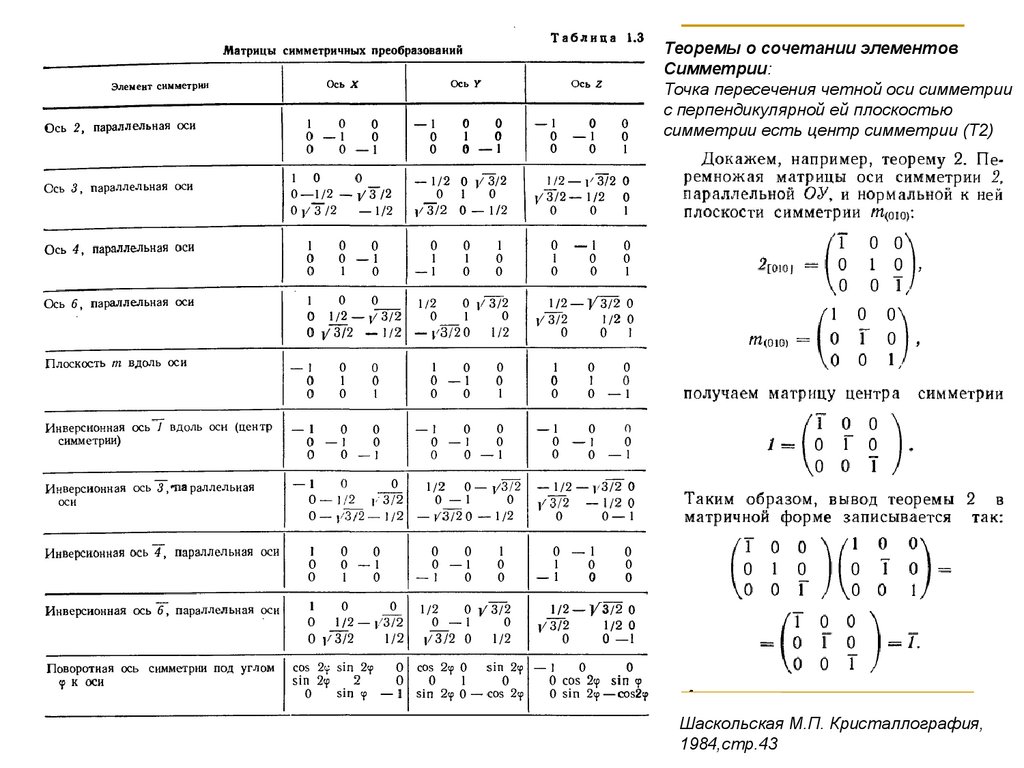
Теоремы о сочетании элементов
Симметрии:
Точка пересечения четной оси симметрии
с перпендикулярной ей плоскостью
симметрии есть центр симметрии (Т2)
Шаскольская М.П. Кристаллография,
1984,стр.43

19.

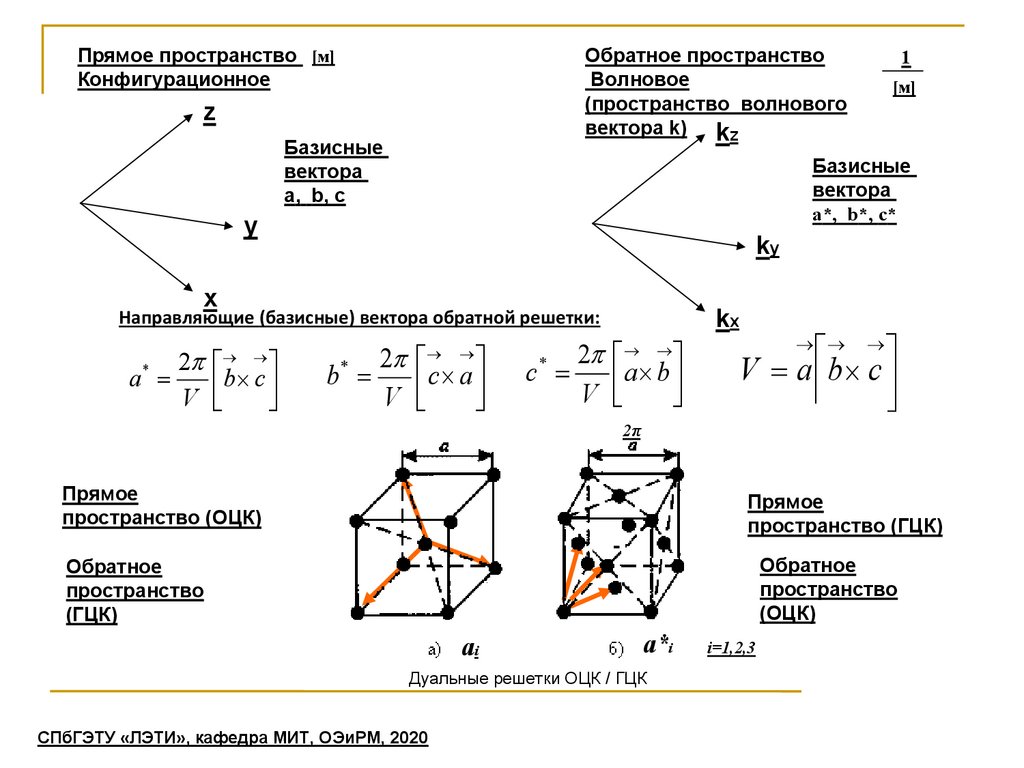
Прямое пространство [м]
Конфигурационное
Обратное пространство
Волновое
(пространство волнового
вектора k) kz
z
Базисные
вектора
a, b, c
ky
x
kx
Направляющие (базисные) вектора обратной решетки:
a*
2
b
c
V
[м]
Базисные
вектора
a*, b*, c*
y
1
2
*
b
c a
V
2
c
a b
V
*
V a b c
2π
Прямое
пространство (ОЦК)
Прямое
пространство (ГЦК)
Обратное
пространство
(ГЦК)
Обратное
пространство
(ОЦК)
ai
a*i
Дуальные решетки ОЦК / ГЦК
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2020
i=1,2,3

20.

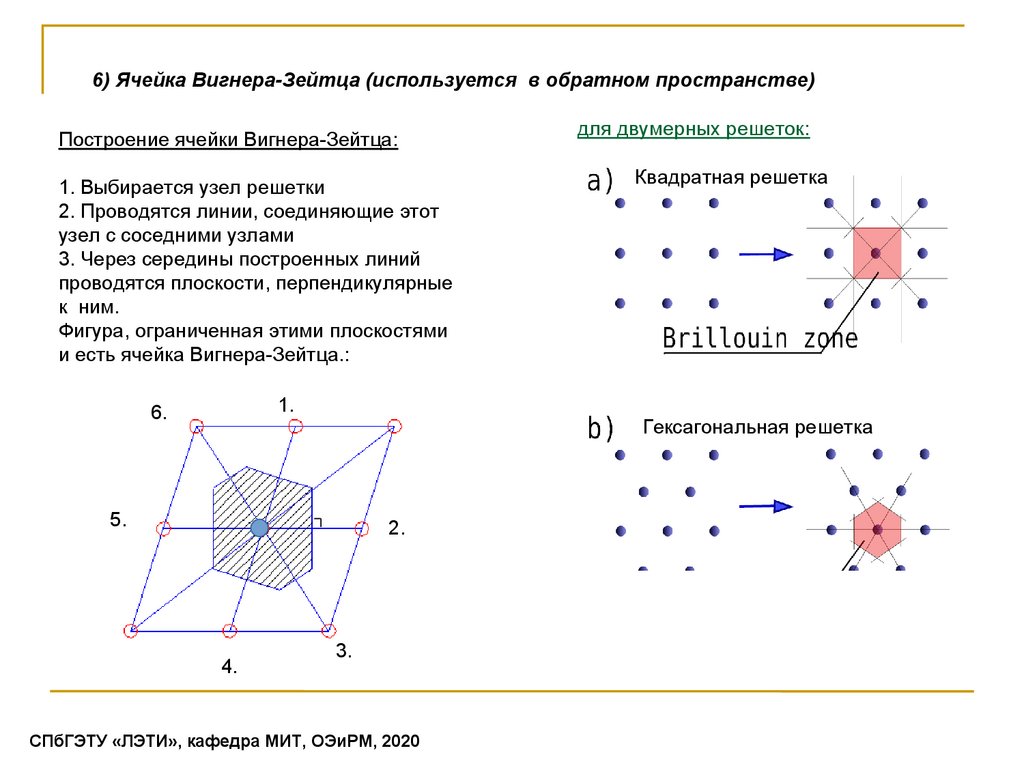
6) Ячейка Вигнера-Зейтца (используется в обратном пространстве)
Построение ячейки Вигнера-Зейтца:
1. Выбирается узел решетки
2. Проводятся линии, соединяющие этот
узел с соседними узлами
3. Через середины построенных линий
проводятся плоскости, перпендикулярные
к ним.
Фигура, ограниченная этими плоскостями
и есть ячейка Вигнера-Зейтца.:
1.
6.
Квадратная решетка
Гексагональная решетка
5.
2.
4.
для двумерных решеток:
3.
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2020

21.

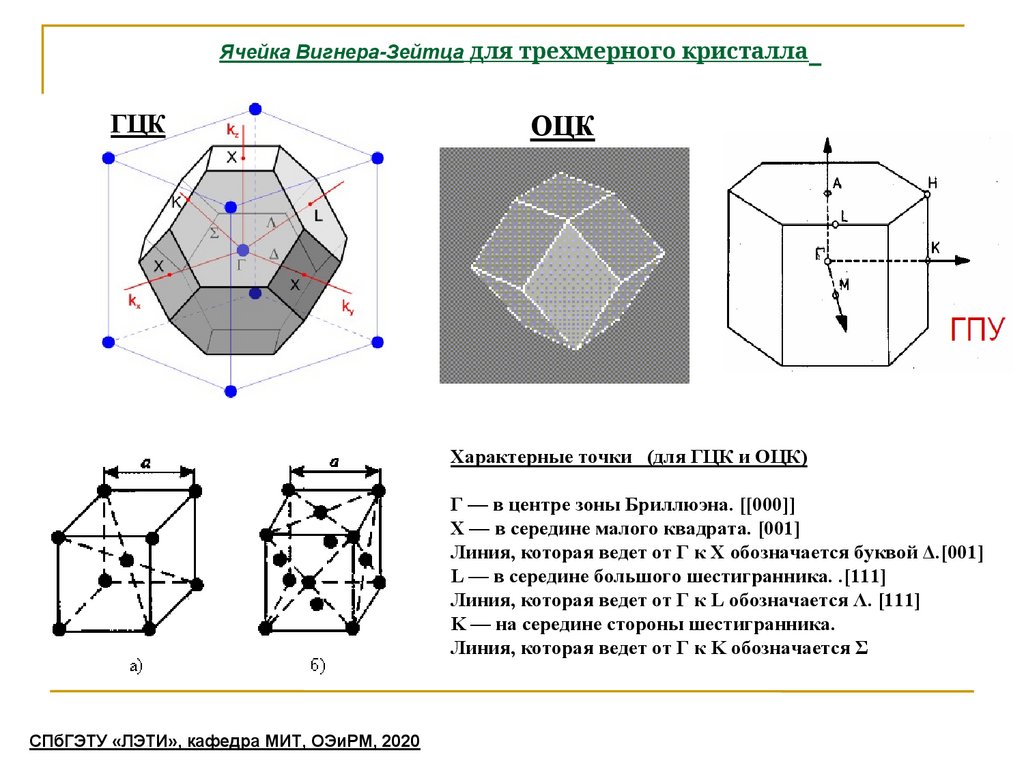
Ячейка Вигнера-Зейтца для трехмерного кристалла
ГЦК
ОЦК
Характерные точки (для ГЦК и ОЦК)
Γ — в центре зоны Бриллюэна. [[000]]
X — в середине малого квадрата. [001]
Линия, которая ведет от Γ к X обозначается буквой Δ.[001]
L — в середине большого шестигранника. .[111]
Линия, которая ведет от Γ к L обозначается Λ. [111]
K — на середине стороны шестигранника.
Линия, которая ведет от Γ к K обозначается Σ
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2020

22.

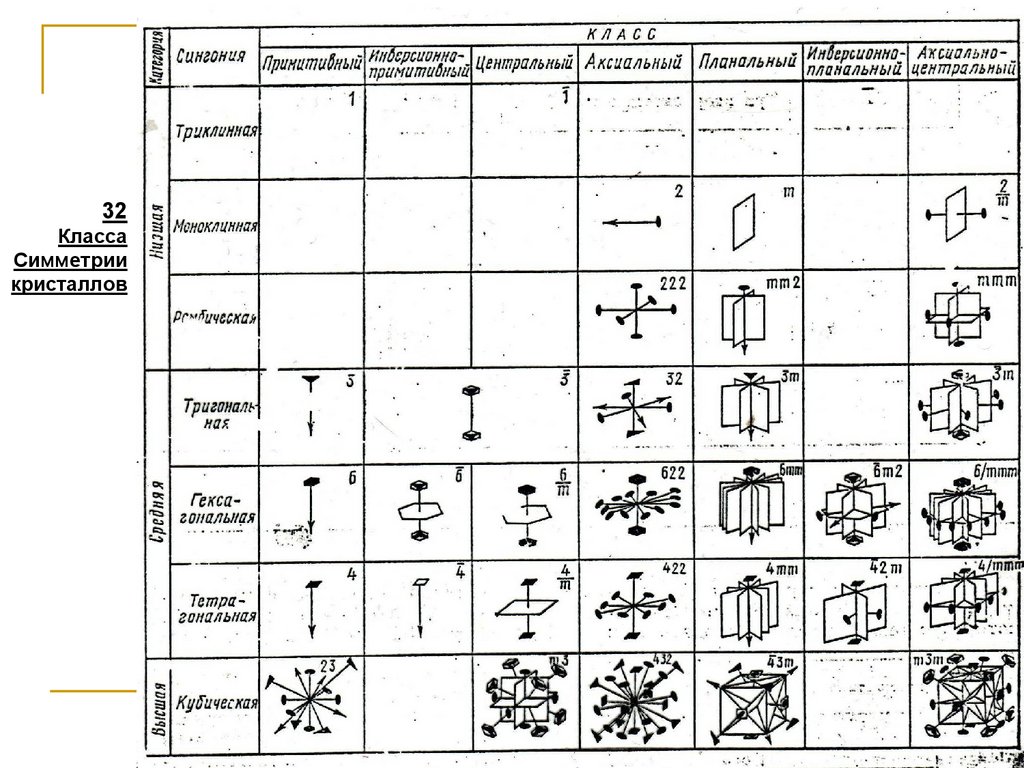
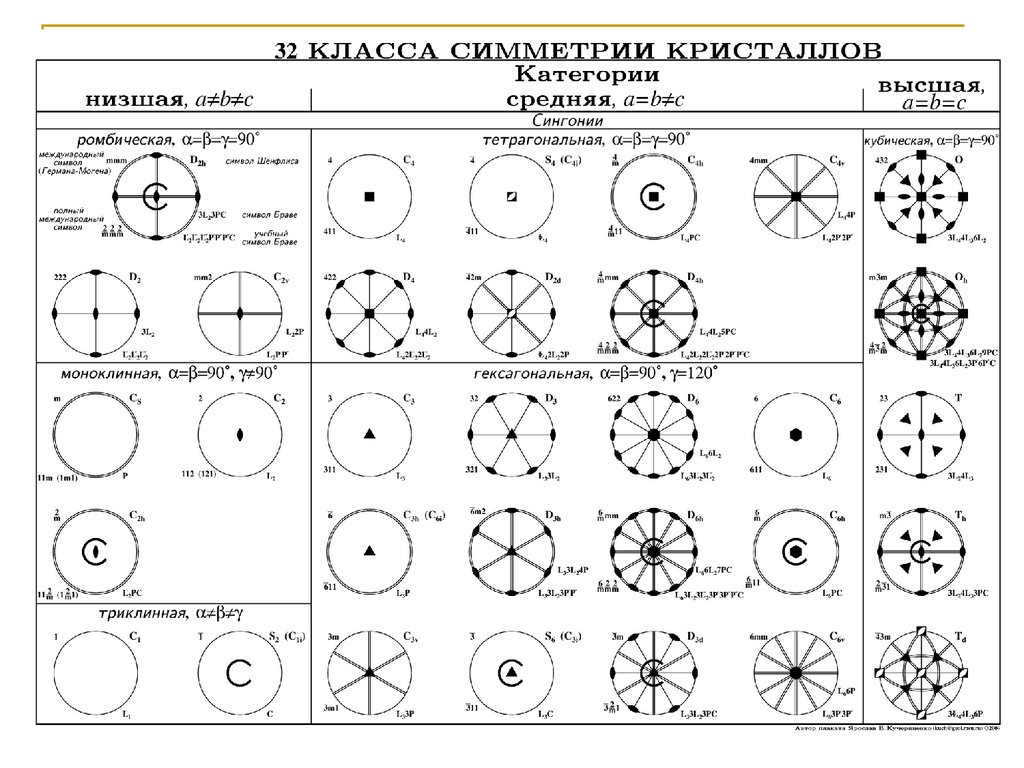
32
Класса
Симметрии
кристаллов

23.

24.

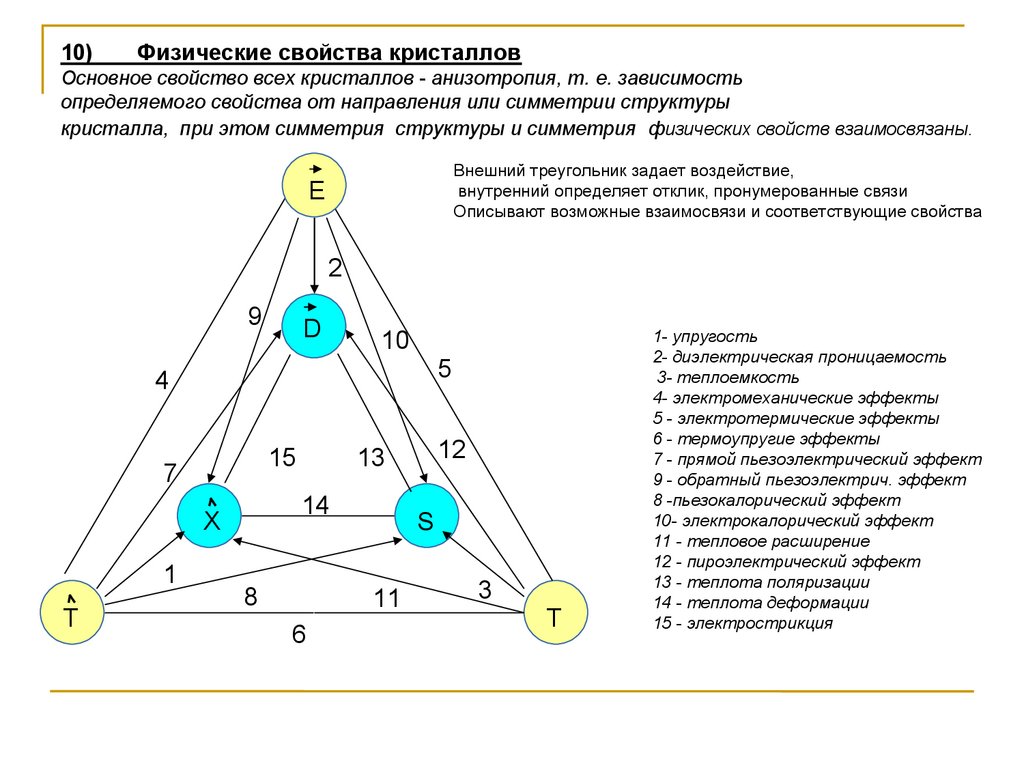
10)
Физические свойства кристаллов
Основное свойство всех кристаллов - анизотропия, т. е. зависимость
определяемого свойства от направления или симметрии структуры
кристалла, при этом симметрия структуры и симметрия физических свойств взаимосвязаны.
Внешний треугольник задает воздействие,
внутренний определяет отклик, пронумерованные связи
Описывают возможные взаимосвязи и соответствующие свойства
E
2
9
D
10
5
4
15
7
14
X
1
T
12
13
8
S
11
6
3
T
1- упругость
2- диэлектрическая проницаемость
3- теплоемкость
4- электромеханические эффекты
5 - электротермические эффекты
6 - термоупругие эффекты
7 - прямой пьезоэлектрический эффект
9 - обратный пьезоэлектрич. эффект
8 -пьезокалорический эффект
10- электрокалорический эффект
11 - тепловое расширение
12 - пироэлектрический эффект
13 - теплота поляризации
14 - теплота деформации
15 - электрострикция

25.

11)
Принципы кристаллофизики
Принцип Неймана
постулат, устанавливающий связь симметрии макроскопических физических свойств
кристалла с симметрией его внешней формы.
Согласно этому принципу, группа симметрии любого спонтанно присущего
кристаллу физического свойства должна включать в себя операции симметрии
точечной группы симметрии кристалла
Принцип суперпозиции Кюри (1894г)
-принцип, согласно которому кристалл под внешним
воздействием изменяет свою точечную симметрию так, что
складывается дисимметрия, т.е. кристалл сохраняет лишь элементы
симметрии, общие с элементами симметрии воздействия.
Симметрия воздействия описывается
предельными классами симметрии Кюри
Принцип Неймана связывает симметрию свойств кристалла с симметрией кристалла до
воздействия, в то время как принцип суперпозиции Кюри позволяет определить
симметрию кристалла после воздействия.
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

26.

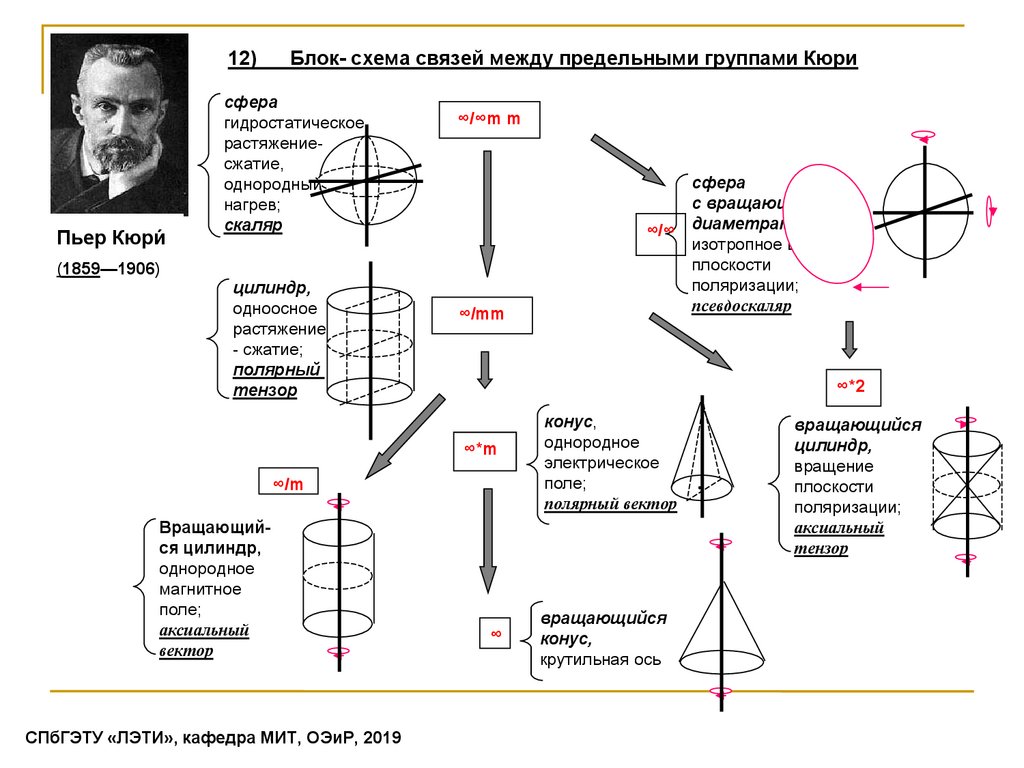
12)
Пьер Кюри́
Блок- схема связей между предельными группами Кюри
сфера
гидростатическое
растяжениесжатие,
однородный
нагрев;
скаляр
∞/∞m m
(1859—1906)
цилиндр,
одноосное
растяжение
- сжатие;
полярный
тензор
∞/mm
∞*2
∞*m
∞/m
Вращающийся цилиндр,
однородное
магнитное
поле;
аксиальный
вектор
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
сфера
с вращающимися
∞/∞ диаметрами,
изотропное вращение
плоскости
поляризации;
псевдоскаляр
∞
конус,
однородное
электрическое
поле;
полярный вектор
вращающийся
конус,
крутильная ось
вращающийся
цилиндр,
вращение
плоскости
поляризации;
аксиальный
тензор

27.

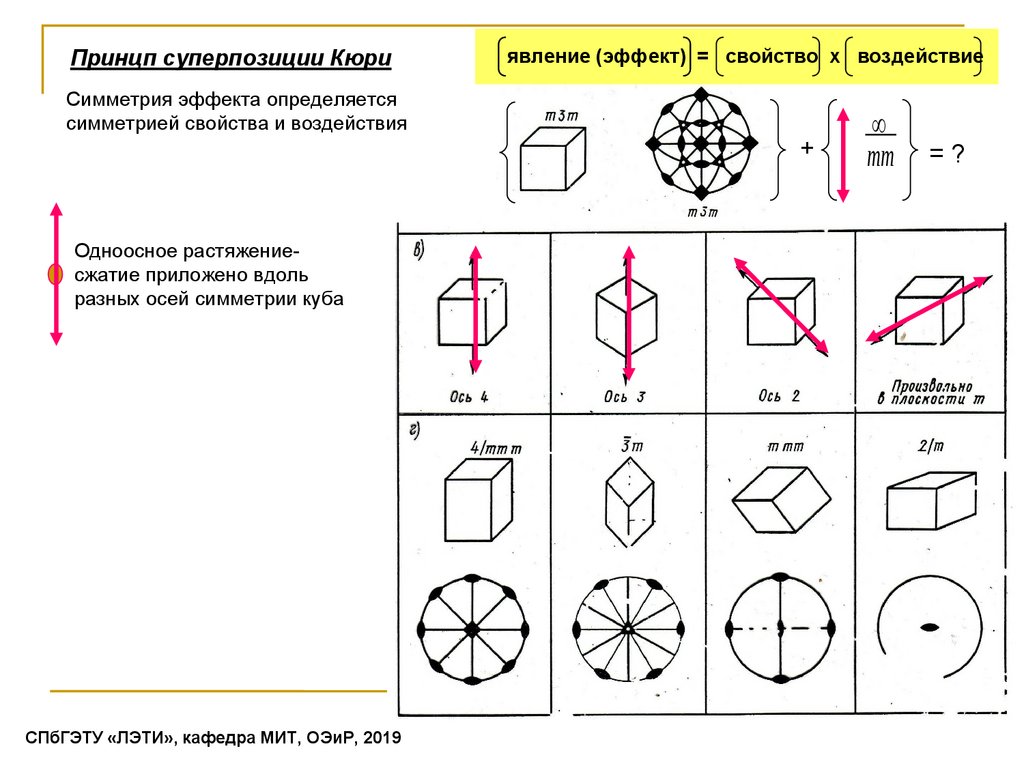
Принцп суперпозиции Кюри
явление (эффект) = свойство x воздействие
Симметрия эффекта определяется
симметрией свойства и воздействия
+
Одноосное растяжениесжатие приложено вдоль
разных осей симметрии куба
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
∞
mm
=?

28.

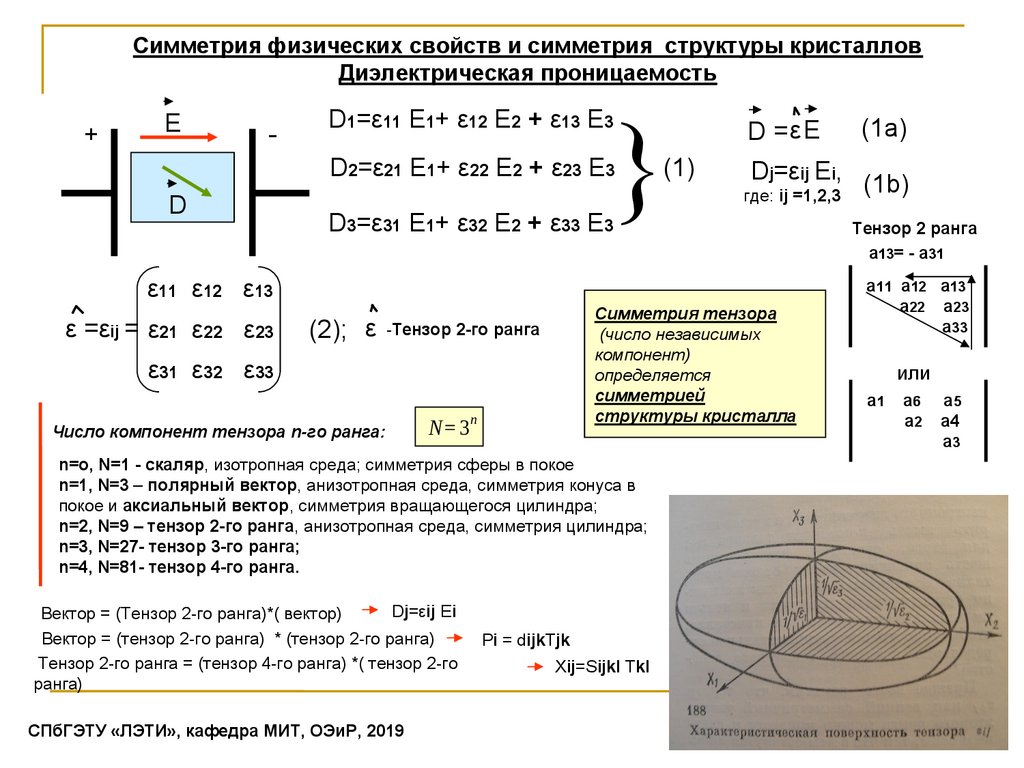
Симметрия физических свойств и симметрия структуры кристаллов
Диэлектрическая проницаемость
+
E
-
}
D1=ε11 E1+ ε12 E2 + ε13 E3
D2=ε21 E1+ ε22 E2 + ε23 E3
D
(1)
D =εE
Dj=εij Ei,
где: ij =1,2,3
D3=ε31 E1+ ε32 E2 + ε33 E3
ε11 ε12 ε13
ε =εij = ε21 ε22 ε23
Симметрия тензора
(число независимых
компонент)
определяется
симметрией
структуры кристалла
(2); ε -Тензор 2-го ранга
ε31 ε32 ε33
N= 3
Число компонент тензора n-го ранга:
n
n=o, N=1 - скаляр, изотропная среда; симметрия сферы в покое
n=1, N=3 – полярный вектор, анизотропная среда, симметрия конуса в
покое и аксиальный вектор, симметрия вращающегося цилиндра;
n=2, N=9 – тензор 2-го ранга, анизотропная среда, симметрия цилиндра;
n=3, N=27- тензор 3-го ранга;
n=4, N=81- тензор 4-го ранга.
Вектор = (Тензор 2-го ранга)*( вектор)
Dj=εij Ei
Вектор = (тензор 2-го ранга) * (тензор 2-го ранга)
Тензор 2-го ранга = (тензор 4-го ранга) *( тензор 2-го
ранга)
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
Pi = dijkTjk
Xij=Sijkl Tkl
(1a)
(1b)
Тензор 2 ранга
а13= - а31
а11 а12 а13
а22 а23
а33
или
а1
а6
а2
а5
а4
а3

29.

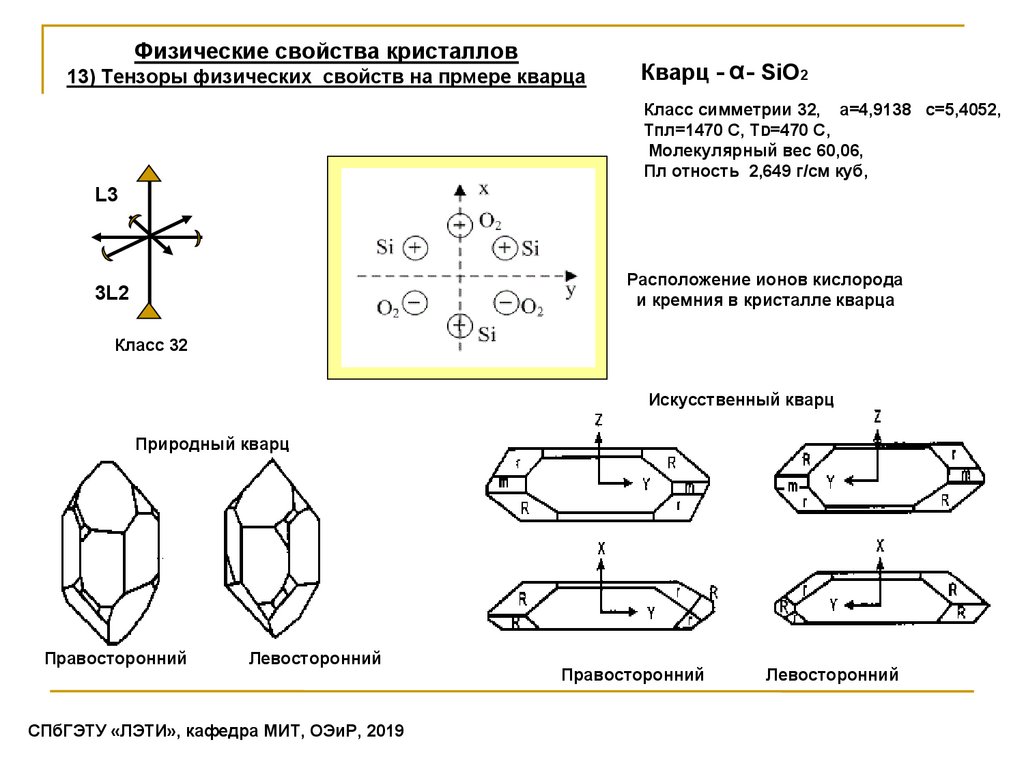
Физические свойства кристаллов
13) Тензоры физических свойств на прмере кварца
Кварц - α- SiO2
Класс симметрии 32, а=4,9138 с=5,4052,
Тпл=1470 С, ТD=470 C,
Молекулярный вес 60,06,
Пл отность 2,649 г/см куб,
L3
Расположение ионов кислорода
и кремния в кристалле кварца
3L2
Класс 32
Искусственный кварц
Природный кварц
Правосторонний
Левосторонний
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
Правосторонний
Левосторонний

30.

Симметрия тензора (число независимых компонент) определяется
симметрией структуры кристалла
Диэлектрические
свойства
Упругие
свойства
Пьезоэлектрические
свойства
Pi = dijkTjk
Dj=εij Ei
Тензор 2 ранга
Xij=Sijkl Tkl
Тензор 3 ранга
d11 d11
Тензор 4 ранга
d14
d11 2d11
ε11
0
0
0
ε33
ε11
ε11=4,58
ε33=4,71
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
d11 = 2,31 (10E-12)K/Н
d14 = 0,727
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
для кварца
Тензор
диэлектрической
проницаемости
Тензор
пьезомодулей
εij
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
djk
Тензор деформации Xij
Тензор напряжений Tkl
Тензор жесткости Sijkl

31.

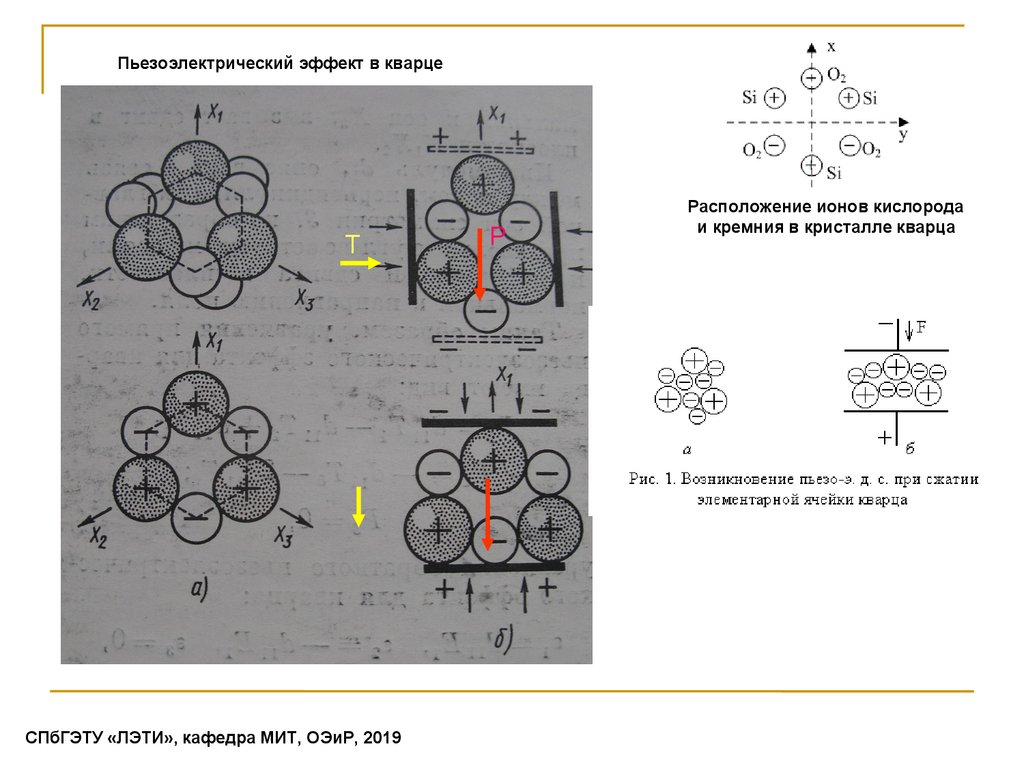
Пьезоэлектрический эффект в кварце
T
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
P
Расположение ионов кислорода
и кремния в кристалле кварца

32.

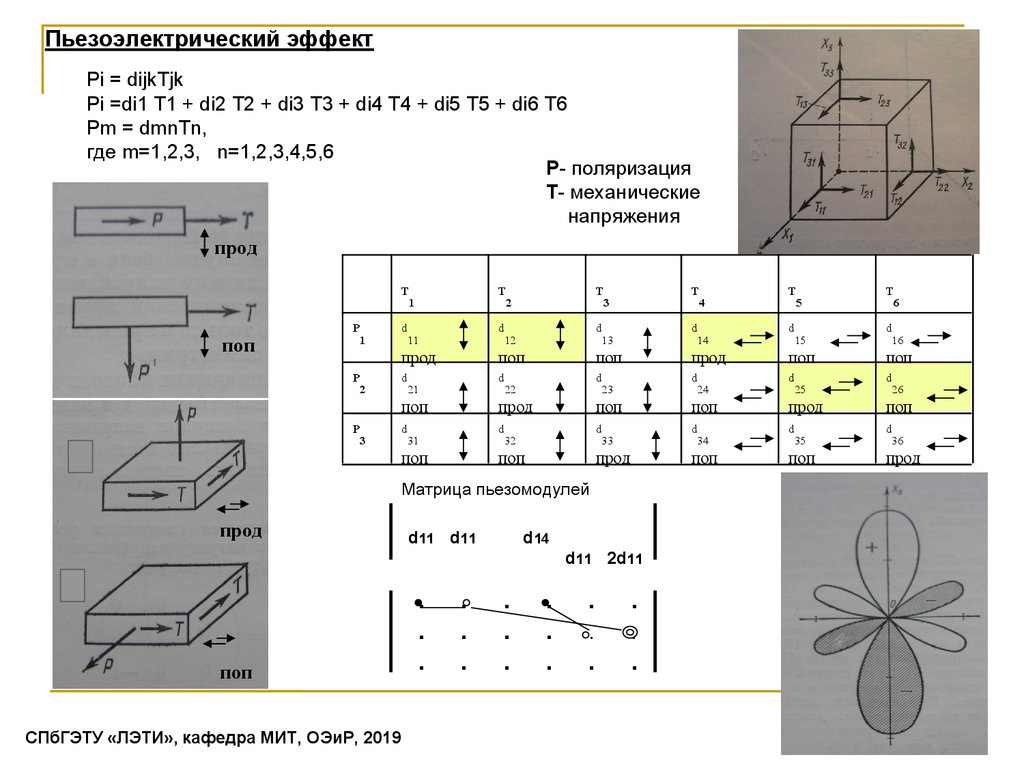
Пьезоэлектрический эффект
Pi = dijkTjk
Pi =di1 T1 + di2 T2 + di3 T3 + di4 T4 + di5 T5 + di6 T6
Pm = dmnTn,
где m=1,2,3, n=1,2,3,4,5,6
Р- поляризация
Т- механические
напряжения
прод
Т
поп
Р
1
Р
2
Р
3
d
Т
1
d
11
Т
2
d
12
Т
3
d
13
15
Т
d
6
16
поп
прод
поп
поп
d
d
d
d
d
d
21
22
23
24
25
26
поп
прод
поп
поп
прод
поп
d
d
d
d
d
d
31
32
поп
33
прод
d11 d11
.
.
.
.
.
.
d14
.
.
.
.
.
.
.
.
.
34
поп
d11 2d11
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019
d
5
поп
Матрица пьезомодулей
поп
14
Т
прод
поп
прод
4
.
.
.
35
поп
36
прод

33.

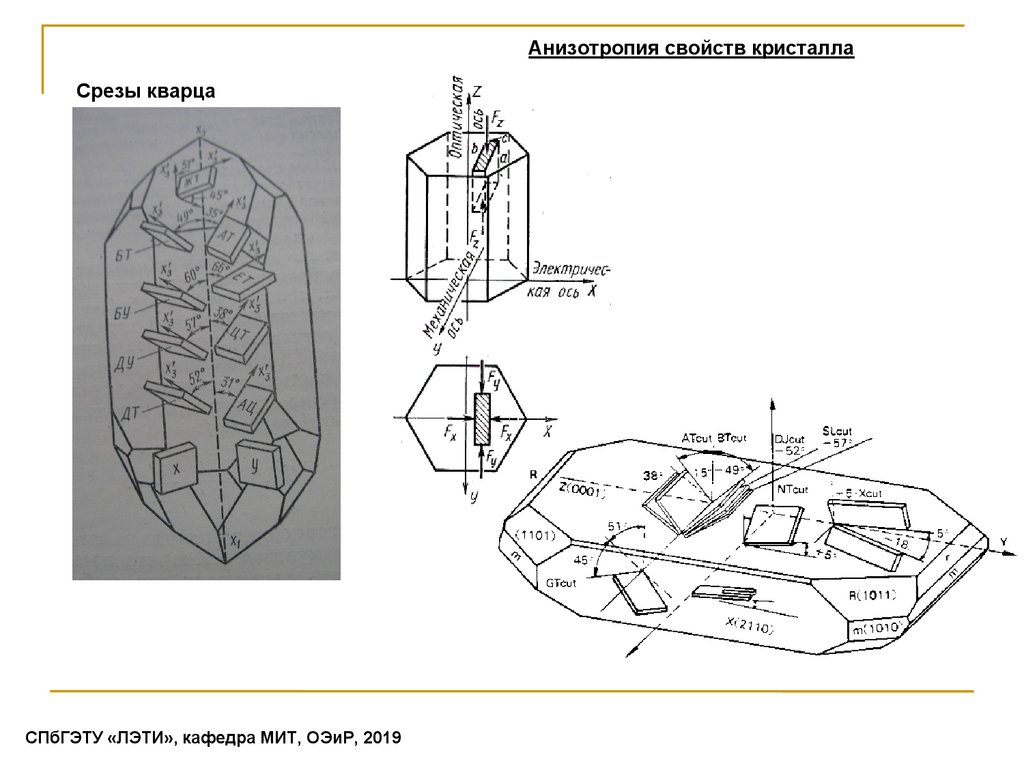
Анизотропия свойств кристалла
Срезы кварца
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

34.

Для обозначения срезов монокристаллов применяется система декартовых координат, привязанная к
идеализированным кристаллам. В самом простом случае срез (называемый стандартным) может совпадать с
плоскостью, определяемой двумя осями координат, и может быть задан с помощью одной буквы X, Y или Z
(например, Y-срез – это срез, выполненный в плоскости XZ, нормаль к которой совпадает с осью Y)
Условное обозначение первоначальной ориентации состоит из двух букв, соответствующих обозначениям
осей, при этом первая буква соответствует той оси, параллельно которой расположена толщина пластины (s),
вторая – параллельно которой расположена длина пластины (l). За толщину пластины принимают ее наименьший
размер, за длину – наибольший.
Повернутые срезы обозначаются введением дополнительных
букв (l, b, s), указывающих ребро пластины, относительно которой
осуществляется поворот, и цифр, обозначающих угол поворота (угол
отсчитывается против часовой стрелки, если смотреть на ребро с
положительного направления оси.
Например, срез кварца YX l/+41 получен путем одного поворота пластины
YX-среза вокруг оси, совпадающей с длиной пластины, на угол +41.
трехповоротный срез кварца YXslb/–20/–35,5/20

35.

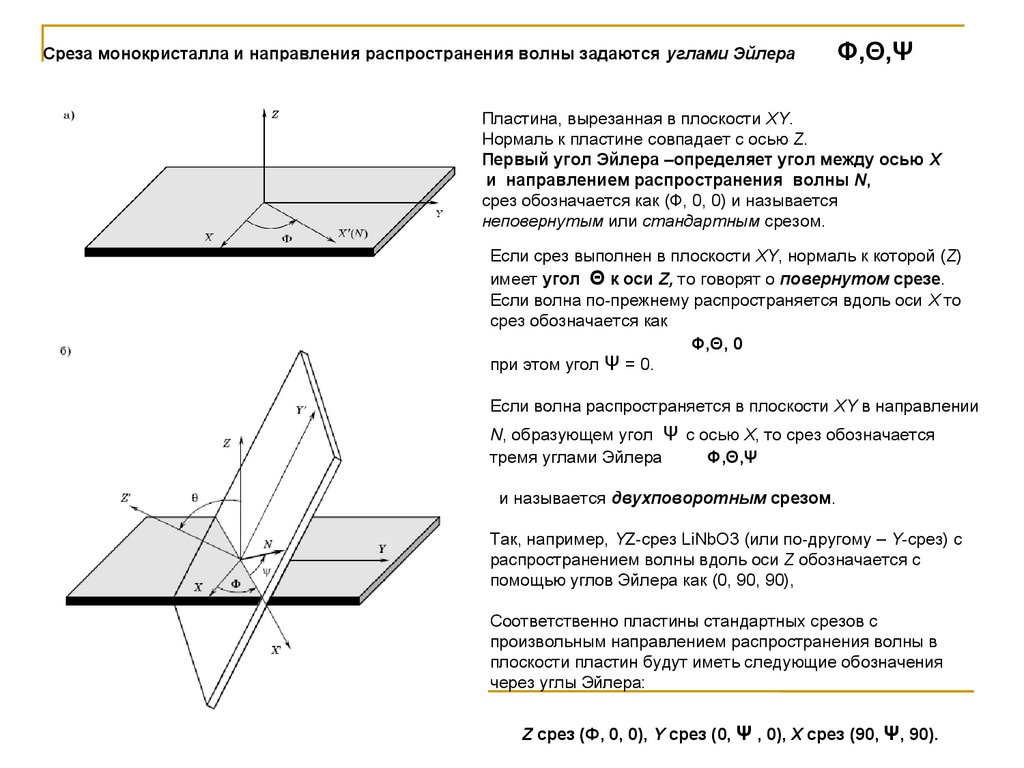
Cреза монокристалла и направления распространения волны задаются углами Эйлера
Φ,Θ,Ψ
Пластина, вырезанная в плоскости XY.
Нормаль к пластине совпадает с осью Z.
Первый угол Эйлера –определяет угол между осью X
и направлением распространения волны N,
срез обозначается как (Ф, 0, 0) и называется
неповернутым или стандартным срезом.
Если срез выполнен в плоскости XY, нормаль к которой (Z)
имеет угол Θ к оси Z, то говорят о повернутом срезе.
Если волна по-прежнему распространяется вдоль оси X то
срез обозначается как
Φ,Θ, 0
при этом угол Ψ = 0.
Если волна распространяется в плоскости XY в направлении
N, образующем угол Ψ с осью X, то срез обозначается
Φ,Θ,Ψ
тремя углами Эйлера
и называется двухповоротным срезом.
Так, например, YZ-срез LiNbO3 (или по-другому – Y-срез) с
распространением волны вдоль оси Z обозначается с
помощью углов Эйлера как (0, 90, 90),
Соответственно пластины стандартных срезов с
произвольным направлением распространения волны в
плоскости пластин будут иметь следующие обозначения
через углы Эйлера:
Z срез (Ф, 0, 0), Y срез (0, Ψ , 0), X срез (90, Ψ, 90).

36.

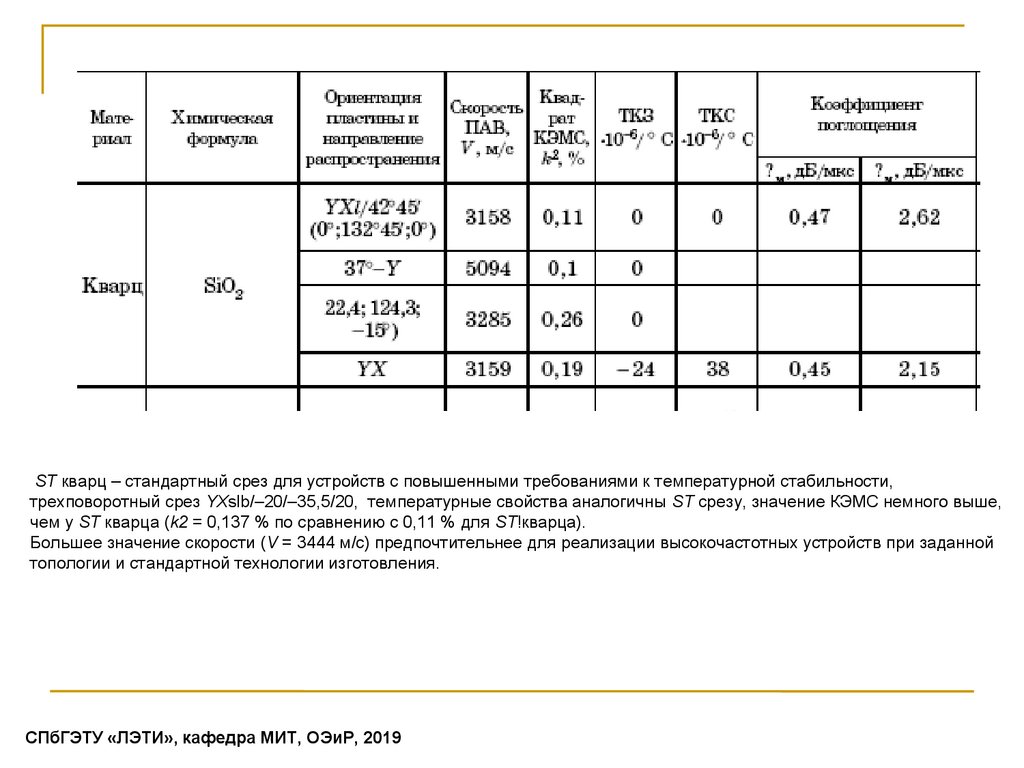
ST кварц – стандартный срез для устройств с повышенными требованиями к температурной стабильности,
трехповоротный срез YXslb/–20/–35,5/20, температурные свойства аналогичны ST срезу, значение КЭМС немного выше,
чем у ST кварца (k2 = 0,137 % по сравнению с 0,11 % для ST!кварца).
Большее значение скорости (V = 3444 м/с) предпочтительнее для реализации высокочастотных устройств при заданной
топологии и стандартной технологии изготовления.
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019

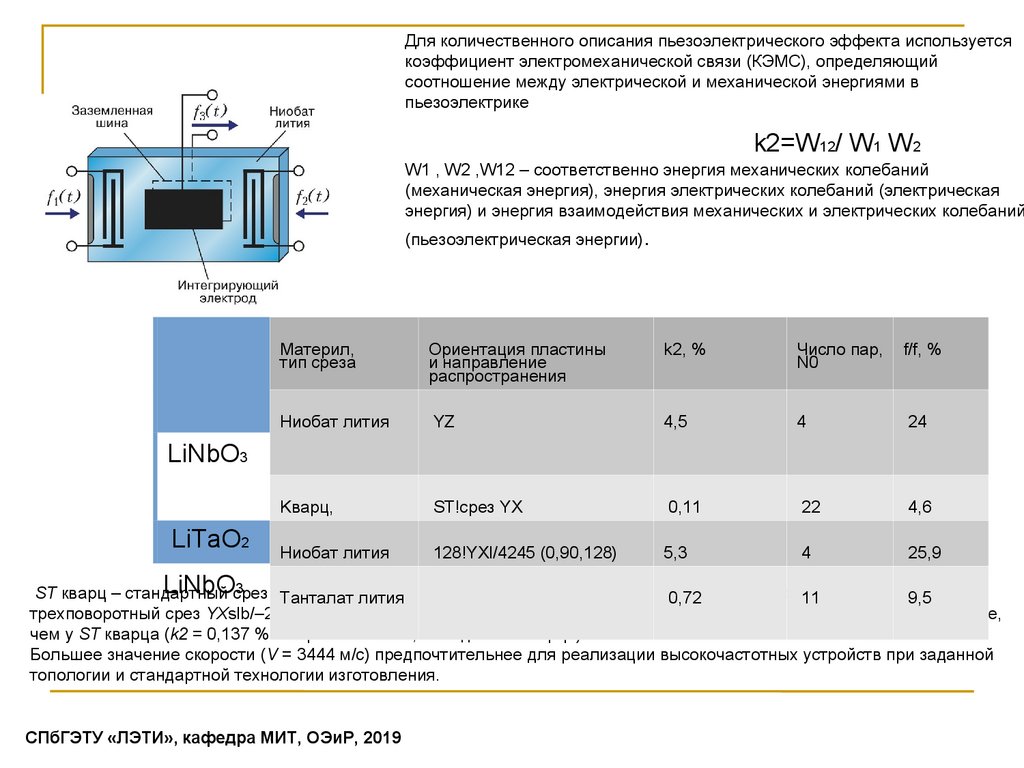
37.

Для количественного описания пьезоэлектрического эффекта используется
коэффициент электромеханической связи (КЭМС), определяющий
соотношение между электрической и механической энергиями в
пьезоэлектрике
k2=W12/ W1 W2
W1 , W2 ,W12 – соответственно энергия механических колебаний
(механическая энергия), энергия электрических колебаний (электрическая
энергия) и энергия взаимодействия механических и электрических колебаний
(пьезоэлектрическая энергии).
Материл,
тип среза
Ориентация пластины
и направление
распространения
k2, %
Число пар,
N0
f/f, %
Ниобат лития
YZ
4,5
4
24
Kварц,
ST!срез YX
0,11
22
4,6
Ниобат лития
128!YXl/4245 (0,90,128)
5,3
4
25,9
LiNbO3
LiTaO2
LiNbOсрез
3
ST кварц – стандартный
для
устройств
с повышенными требованиями к температурной
стабильности,
Танталат
лития
0,72
11
9,5
трехповоротный срез YXslb/–20/–35,5/20, температурные свойства аналогичны ST срезу, значение КЭМС немного выше,
чем у ST кварца (k2 = 0,137 % по сравнению с 0,11 % для ST!кварца).
Большее значение скорости (V = 3444 м/с) предпочтительнее для реализации высокочастотных устройств при заданной
топологии и стандартной технологии изготовления.
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2019