Геометрические характеристики плоских сечений

1. Геометрические характеристики плоских сечений

Доцент кафедры
самолетостроения
К.т.н Мухин Д.В.

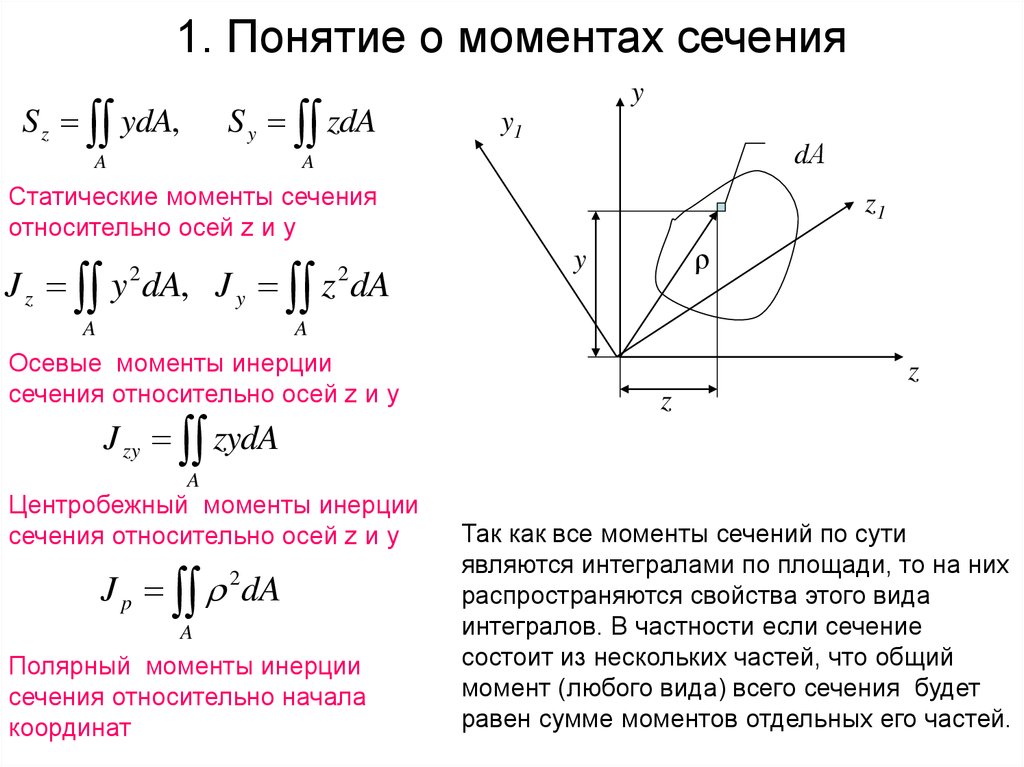
2. 1. Понятие о моментах сечения

S z ydA,
S y zdA
A
y
y1
dА
A
Статические моменты сечения
относительно осей z и y
J z y dA, J y z dA
2
2
A
z1
ρ
y
A
Осевые моменты инерции
сечения относительно осей z и y
J zy zydA
z
z
A
Центробежный моменты инерции
сечения относительно осей z и y
J p 2 dA
A
Полярный моменты инерции
сечения относительно начала
координат
Так как все моменты сечений по сути
являются интегралами по площади, то на них
распространяются свойства этого вида
интегралов. В частности если сечение
состоит из нескольких частей, что общий
момент (любого вида) всего сечения будет
равен сумме моментов отдельных его частей.

3.

Моменты Jz, Jy, Jp всегда положительны и никогда не равняются нулю, а Sy,
Sz Jzy— могут быть положительными, отрицательными и равными нулю.
Зависимость между осевыми и полярными моментами инерции можно
получить, если подставить в выражение Jp равенство
2 y2 z2
тогда
J p 2 dA y 2 z 2 dA y 2 dA z 2 dA J y J z
A
A
A
A
Полярный момент инерции сечения относительно точки равен сумме его
моментов инерции относительно любых взаимно перпендикулярных осей,
проходящих через эту точку.
Следствие. Сумма осевых моментов инерции сечения относительно
любых взаимно перпендикулярных осей, проходящих через данную точку,
есть величина постоянная:
J y J z J y1 J z1 const

4. 2. Понятие о центре тяжести сечения и свойство статическою момента

yс
Центром тяжести сечения
называется точка, координаты
которой определяются по формулам:
Sy
Sz
yC ; zC
A
A
y
dA
y
yс
С z
Если положение центра тяжести
сечения известно, то
S y zc A; S z yc A
zс
z
zс
Статический момент сечения относительно оси равняется его площади,
умноженной на расстояние от центра тяжести сечения до этой оси.
Если ось y проходит через центр тяжести сечения, то
zc 0 S y 0
Статический момент сечения относительно оси, проходящей через его
центр тяжести (относительно центральной оси), равен нулю

5.

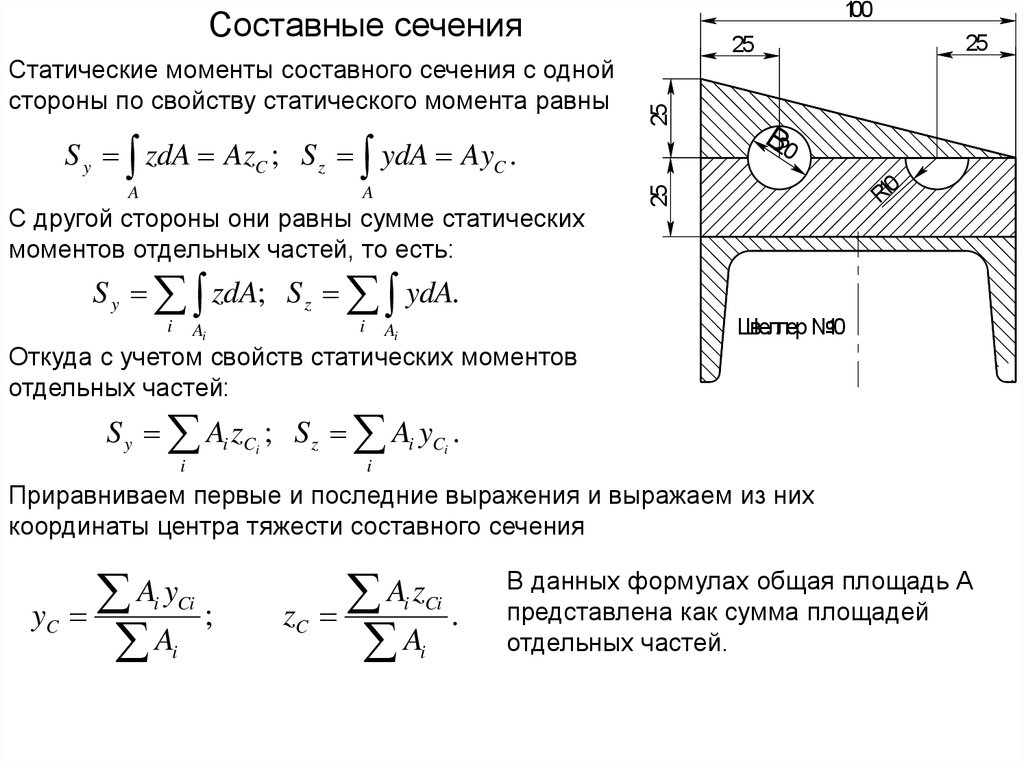
100
Составные сечения
S y zdA AzC ; S z ydA AyC .
A
A
С другой стороны они равны сумме статических
моментов отдельных частей, то есть:
S y zdA; S z ydA.
i
i
Ai
Ai
25
B20
0
R1
25
Статические моменты составного сечения с одной
стороны по свойству статического момента равны
25
25
Швеллер №10
Откуда с учетом свойств статических моментов
отдельных частей:
S y Ai zCi ; S z Ai yCi .
i
i
Приравниваем первые и последние выражения и выражаем из них
координаты центра тяжести составного сечения
yC
Ay
A
i
Ci
i
;
zC
Az
A
i Ci
i
.
В данных формулах общая площадь А
представлена как сумма площадей
отдельных частей.

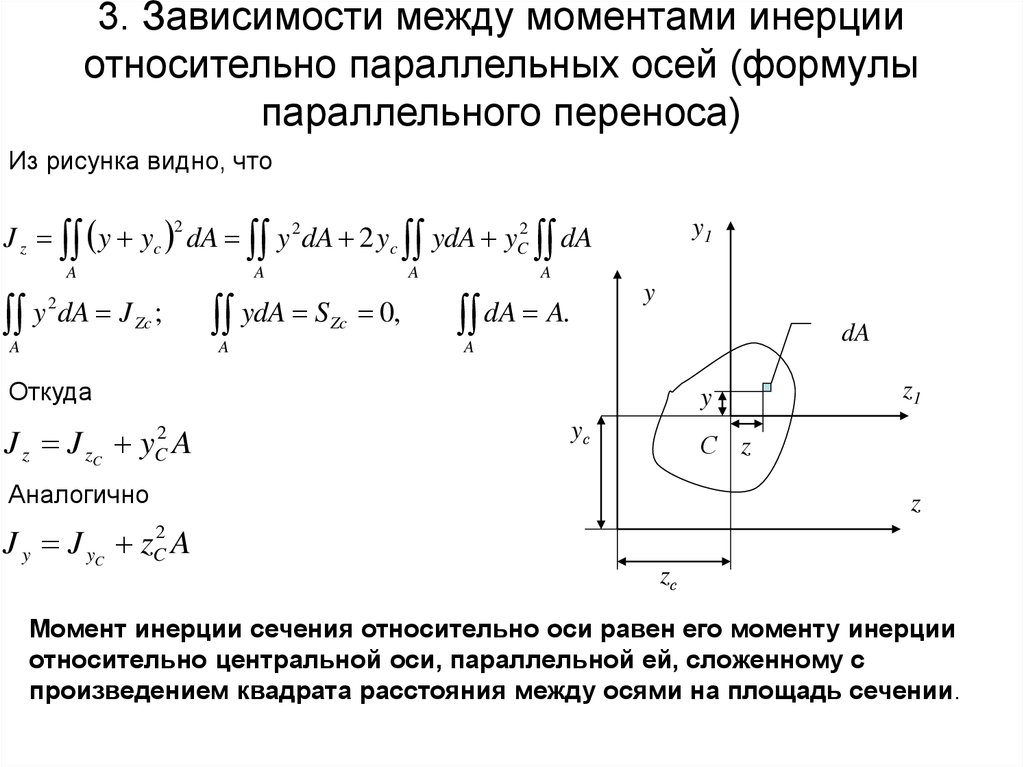
6. 3. Зависимости между моментами инерции относительно параллельных осей (формулы параллельного переноса)

Из рисунка видно, что
J z y yc dA y 2 dA 2 yc ydA yC2 dA
y1
2
A
y dA J
A
2
Zc
;
A
ydA S
A
A
Zc
0,
A
y
dA A.
dA
A
Откуда
J z J zC yC2 A
y
yс
С z
Аналогично
J y J yC zC2 A
z1
z
zс
Момент инерции сечения относительно оси равен его моменту инерции
относительно центральной оси, параллельной ей, сложенному с
произведением квадрата расстояния между осями на площадь сечении.

7.

Аналогично
J zy y yc z zc dA zydA yc zdA zc ydA zC yC dA
A
zydA J
A
A
ZcYc
A
A
A
; zdA SYc 0
A
Следовательно
J zy J zc yc zC yC A
Центробежный момент инерции сечения относительно
перпендикулярных осей равняется центробежному моменту инерции
относительно центральных осей, параллельных им, сложенному с
произведением расстояний между осями на площадь сечения

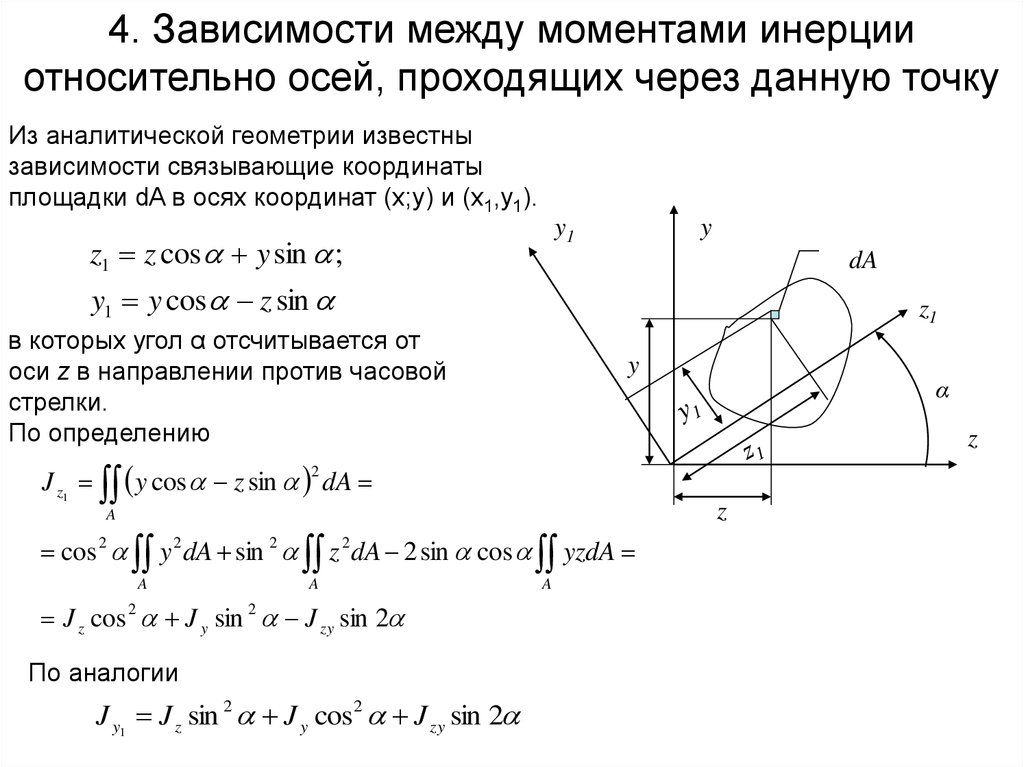
8. 4. Зависимости между моментами инерции относительно осей, проходящих через данную точку

Из аналитической геометрии известны
зависимости связывающие координаты
площадки dA в осях координат (х;y) и (x1,y1).
y1
z1 z cos y sin ;
y
dA
y1 y cos z sin
z1
в которых угол α отсчитывается от
оси z в направлении против часовой
стрелки.
По определению
y
α
z
J z1 y cos z sin dA
2
z
A
cos 2 y 2 dA sin 2 z 2 dA 2 sin cos yzdA
A
A
J z cos 2 J y sin 2 J zy sin 2
По аналогии
J y1 J z sin 2 J y cos 2 J zy sin 2
A

9.

И то же самое для центробежного момента
J z1 y1 y sin z cos y cos z sin dA
A
sin cos y 2 dA sin cos z 2 dA cos 2 zydA sin 2 zydA
A
Jz Jy
2
A
A
A
sin 2 J zy cos 2
Для практического применения формулы иногда преобразовывают в вид:
J z1
J y1
Jz Jy
2
Jz Jy
J z1 y1
2
Jz Jy
2
Jz Jy
2
Jz Jy
2
cos 2 J zy sin 2 ;
cos 2 J zy sin 2 ;
sin 2 J zy cos 2 ;

10. 5. Главные оси и главные моменты инерции сечения. Радиусы инерции.

Главными осями сечения, проходящими через
данную точку, называются оси, относительно
которых центробежный момент инерции
равняется нулю.
Главные оси обозначаются цифрами 1 и 2
y
A
2
Моменты инерции относительно главных
осей называются главными
α2
Главные моменты инерции обозначают J1 и J2 ,
причем J1> J2.
Чтобы найти положения главных осей в данной
точке О, выбирают в этой точке оси z и у для
которых Jz,Jy, Jzy определяются проще всего.
Центробежный момент в главных осях (1;2) связан с
центробежным моментом в осях (y;z) зависимостью
J12
Jz Jy
2
sin 2 J zy cos 2 ;
z
α1
1

11.

Так как по определению главных осей центробежный момент J12 должен быть
равен нулю
Jz Jy
sin 2 J zy cos 2 0
2
tg 2 1, 2
откуда
2 J zy
Jy Jz
Находим значения α1, и α2, определяющие соответственно положения первой и
второй главных осей, для чего решаем полученное уравнение
1, 2
2 J zy
1
n
arctg
2
Jy Jz
2
где n – любое целое число
Нас интересуют первые два решения, т.е. n1=0, n2=1 получаем:
2 J zy
1
2 arctg
2
Jy Jz 2
2 J zy
1
1 arctg
2
Jy Jz
Из выражений для α1 и α2 заключаем, что главные оси взаимно перпендикулярны.
После определения α1 и α2 величины главных моментов инерции сечений J1 и J2
находятся по формуле
J1, 2
Jz Jy
2
Jz Jy
2
cos 2 1, 2 J zy sin 2 1, 2

12.

Проведя преобразования можно получить, что
J1, 2
tg 1, 2
1
Jz Jy
2
J z J1, 2
J zy
J
J y 4 J zy2
2
z
Для того чтобы понять смысл понятия главных моментов найдем значение α, при
котором Jz1 и Jу1 достигают экстремальных значений. Для этого
продифференцируем Jz1 по α и производную приравняем нулю
dJ z1
d J z cos 2 J y sin 2 J zy sin 2
d
d
J z 2 sin cos J y 2 sin cos J zy 2 cos 2 0
Откуда
tg 2
2 J zy
Jy Jz
Значения α из формул совпадают со значениями α для главных моментов.
Следовательно, моменты инерции относительно главных осей достигают
экстремальных значений, т. е. главный момент инерции J1, есть наибольший из
всех моментов инерции относительно осей, проходящих через данную точку, а
J2 - наименьший.

13.

Радиусом инерции сечения относительно некоторой оси, например z,
называется величина iz, определяемая из равенства:
J z A iz2
iz
Jz
A
Радиусы инерции, соответствующие главным осям, называют главными
радиусами инерции.
i1
J1
A
i2
J2
A

14. 6. Свойства моментов инерции геометрических фигур

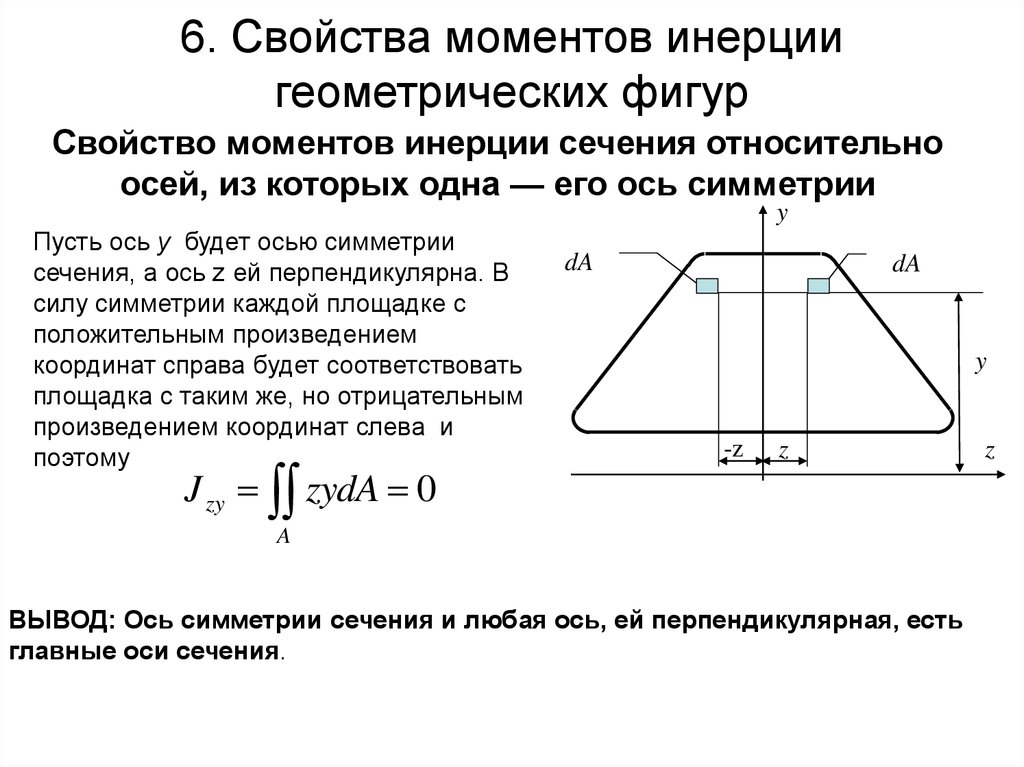
Свойство моментов инерции сечения относительно
осей, из которых одна — его ось симметрии
y
Пусть ось у будет осью симметрии
сечения, а ось z ей перпендикулярна. В
силу симметрии каждой площадке с
положительным произведением
координат справа будет соответствовать
площадка с таким же, но отрицательным
произведением координат слева и
поэтому
J zy zydA 0
dA
dA
y
-z
z
A
ВЫВОД: Ось симметрии сечения и любая ось, ей перпендикулярная, есть
главные оси сечения.
z

15.

Свойство моментов инерции правильных фигур
относительно центральных осей
y
J zy 0, J z J y
Для правильных фигур
α
Для квадрата последнее равенство очевидно, так как он
одинаково расположен относительно осей z и у. Для
остальных фигур это можно доказать следующим
образом: в правильной фигуре всегда найдется ось z1
относительно которой она будет расположена так же.
как относительно оси z, и поэтому Jz1=Jz. Но ранее
показано, что
J z1 J z cos 1 J y sin 1
2
J z J z cos 1 J y sin 1 или J z 1 cos 1 J y sin 1
откуда
z
y
z1
u
α1
α
z
2
или
2
u
2
2
Jz Jy
2
y
z1
α
u
α
Для произвольной оси u, проходящей через центр
J u J z cos 2 J y sin 2 J z cos 2 sin 2 J z
ВЫВОД: Моменты инерции правильных фигур относительно центральных
осей равны и любые взаимно перпендикулярные центральные оси будут
главными
z

16.

Геометрические характеристики некоторых фигур
Фигура
y
Координата ЦТ
Осевые моменты
инерции
Круг
x
Jx Jy
d 4
64
d=2r
Jx Jy
y
Кольцо
x
d1=2r1
r 4
s
3
3
0,05d 4 W W d r 0,1d 3
x
y
4
32
4
d 4
1 с
64
4
1 с 0,05d
4
Тонкостенное кольцо
y
d
x
r 4
4
4
с d1 d
d=2r
S
Jx Jy
10
d 3 s
8
Моменты
сопротивления
r 3 s
Wx Wy
r 3
4
d 3
1 с
32
4
1 с 0,1d 1 с
4
Wx Wy
3
d 2 s
4
r 2 s
d=2r
Полукруг
y
x
yc
d=2r
2d
yc
0,2122d
3
0,4244r
J x 0,00686d 4 0,11r 4
Jy
d 4
128
0,025d 4
Wx 0,0238d 3
Wy
d 3
64
0,05d 3
4

17.

Фигура
y
Координата ЦТ
Квадрат
b4
Jx Jy
12
x
b
Полый
квадрат
y
b b1
Тонкостенный квадрат
y
s
Треугольник
y
h
yc
x
yc
b
h
3
bh 3
Jx
36
bh 3
JU
12
4b 2 s
Wx Wy
3
hb 3
Jy
48
bh 3
J U1
4
u
Трапеция
y
a
h
u1
b 4 b14
Wx Wy
6b
2b3 s
Jx Jy
3
x
a
yc
x
yc
b
u
h b 2a
3 b a
h 3 b 2 4ba a 2
Jx
36 b a
h b4 a4
Jy
48 b a
Моменты
сопротивления
b3
Wx Wy
6
b 4 b14
Jx Jy
12
x
b
Осевые моменты
инерции
bh 2
hb 2
Wx
Wy
24
24
2
bh
Wx
для основания
12
h 2 b 2 4ba a 2
Wx
12 2b a
h b4 a4
Wy
24 b 2 ba

18.

Сопротивление материалов
Раздел: Геометрические характеристики
Расчет моментов инерции сечения,
заданого аналитически
Фигура задана 4-мя кривыми
T
2 15
y ( z) 8 ln ( z) 20 5 ( z 8)
8 2 z
z
Крайние точки
левая
z0 2
правая
zk 10
Проверка расчетных формул на примере квадрата
(включите следующ ие 3 выражения)
T
y ( z) ( 10 z 20 z 10 z 0 z )
z0 0
zk 10
Определение координат точек пересечения кривых
x 1 z 1 начальные приближения
Given
x
y ( z)
Given
x
y ( z)
Given
x
y ( z)
x
y ( z)
0
0
2
x
y ( z)
x
y ( z)
x
y ( z)
x
y ( z)
2
1
3
z 10
Given
1
3
z0
z0
Find
(
z
x
)
y0
y0
z1
Find ( z x)
y1
z2
Find ( z x)
y2
z1
y1
z2
y2
2.3
6.6
7.067
15.643
5.391
2.782
zk
zk 9.362
Find ( z x)
yk
yk 10.724

19.

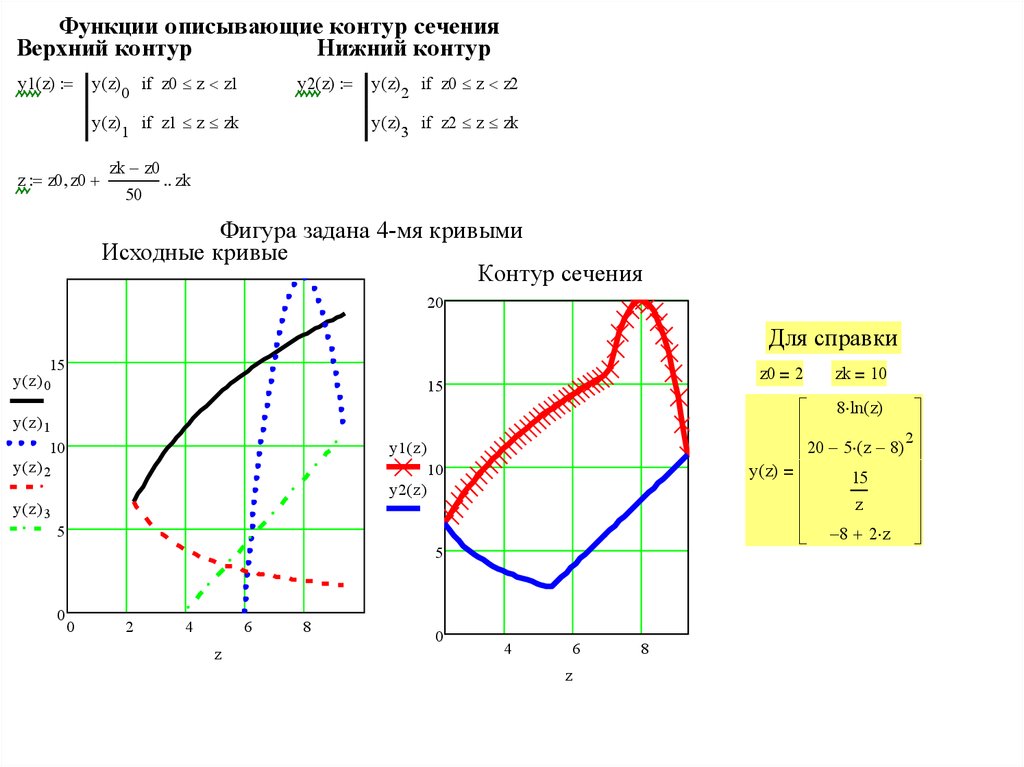
Функции описывающие контур сечения
Верхний контур
Нижний контур
y1( z)
y ( z)
y ( z)
z z0 z0
0
1
if z0 z z1
y2( z)
if z1 z zk
zk z0
50
y ( z)
y ( z)
2
3
if z0 z z2
if z2 z zk
zk
Фигура задана 4-мя кривыми
Исходные кривые
Контур сечения
20
Для справки
15
y ( z) 0
z0
15
y1( z )
y ( z) 2
10
y2( z )
y ( z) 3
5
5
0
0
2
4
6
z
8
0
zk
10
8 ln ( z)
2
20
5
(
z
8
)
y ( z)
15
z
8
2
z
y ( z) 1
10
2
4
6
z
8

20.

Расчет статических моментов S z, Sy
моментов инерции Jz, Jy, Jzy относительно исходных осей,
а также площади A и координат центра тяжести y c и z c .
Jz
zk
Jy
zk
z0
y1( z )
y1( z )
z0
Jzy
zk
z0
y c
Sz
A
2
Jz 6823
y dy dz
y2( z )
zk
Sz
zk
Sy
zk
z0
2
Jy 2386.055
z dy dz
y2( z )
A
z0
y1( z )
z y d y d z z Jzy 3883.595
y2( z )
y c 10.19
z0
zc
Sy
A
y1( z )
y1( z )
y1( z )
1 dy dz
A 57.835
y dy dz
Sz 589.105
z dy dz
Sy 358.277
y2( z )
y2( z )
y2( z )
zc 6.19
Расчет моментов инерции относительно центральных осей,
параллельных исходным
2
Jzc 822.537
Jyc Jy A zc
2
Jyc 166.584
Jzcyc Jzy A zc y c
Jzcyc 234.185
Jzc Jz A y c

21.

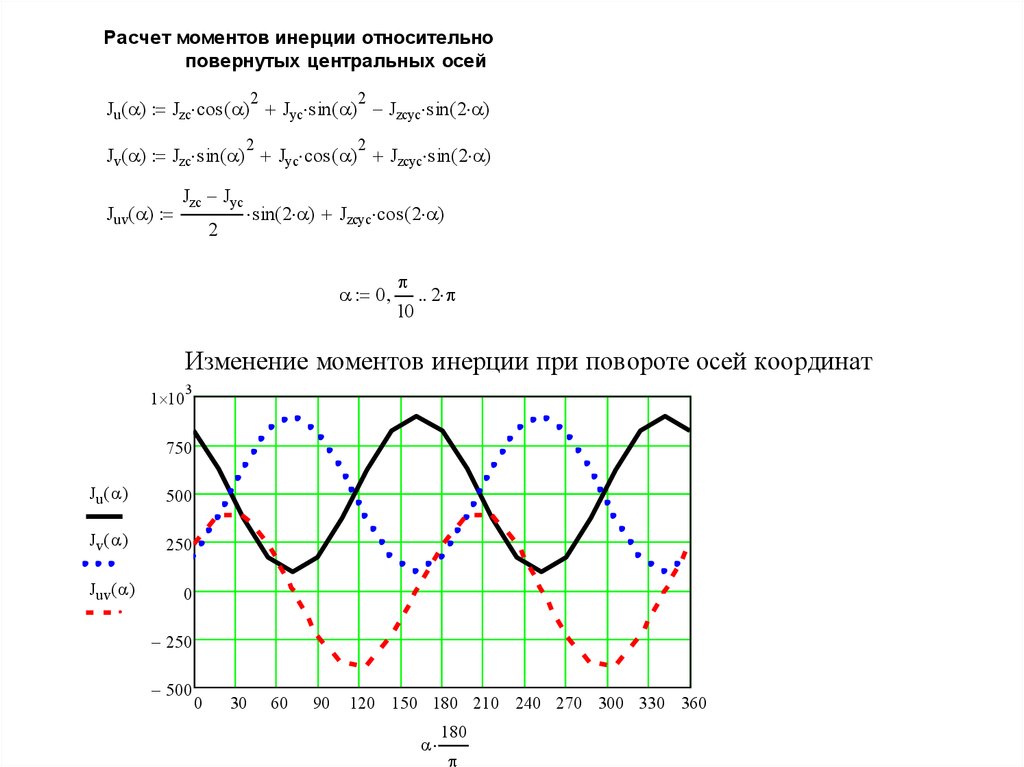
Расчет моментов инерции относительно
повернутых центральных осей
2
2
2
2
Ju( ) Jzc cos ( ) Jyc sin ( ) Jzcyc sin ( 2 )
Jv( ) Jzc sin ( ) Jyc cos ( ) Jzcyc sin ( 2 )
Juv( )
Jzc Jyc
2
sin ( 2 ) Jzcyc cos ( 2 )
0 2
10
Изменение моментов инерции при повороте осей координат
3
1 10
750
Ju( )
500
Jv( )
250
Juv( )
0
250
500
0
30
60
90
120 150 180 210 240 270 300 330 360
180

22.

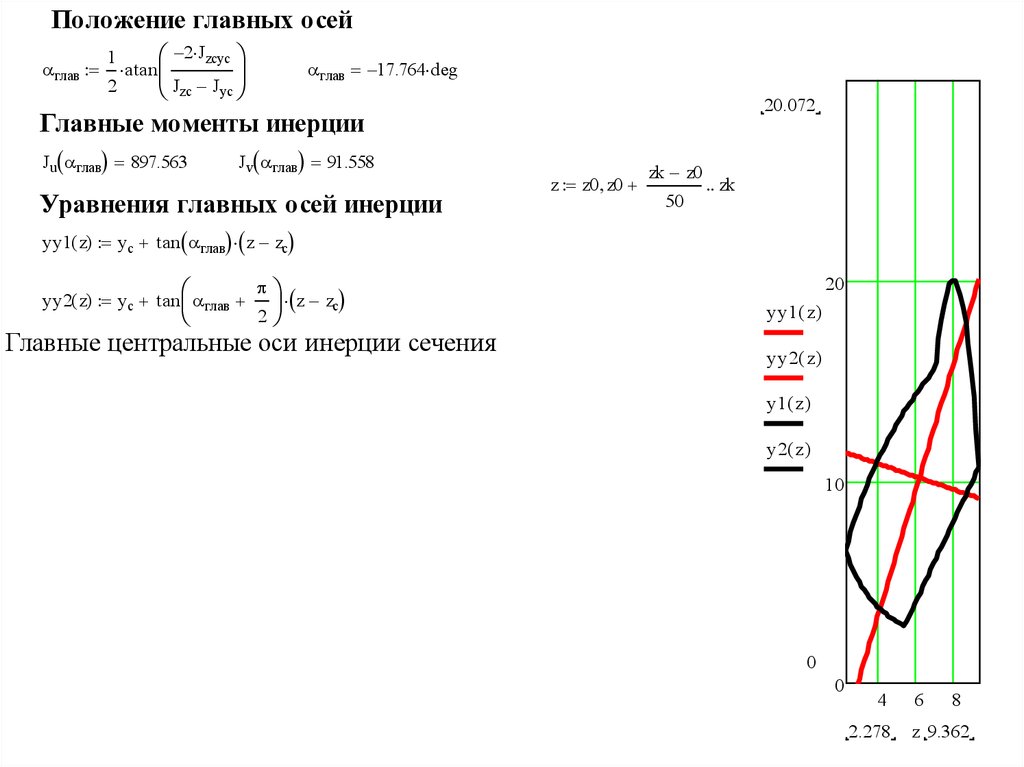
Положение главных осей
глав
1
2
2 Jzcyc
Jzc Jyc
atan
глав 17.764 deg
20.072
Главные моменты инерции
Ju глав 897.563
Jv глав 91.558
Уравнения главных осей инерции
z z0 z0
zk z0
50
zk
yy1( z) y c tan глав z zc
yy2( z) y c tan глав
z z
c
2
20
Главные центральные оси инерции сечения
yy1( z )
yy2( z )
y1( z )
y2( z )
10
0
0
4
2.278
6
8
z 9.362

23.

Сопротивление материалов
Раздел: Геометрические характеристики
20
20
20
20
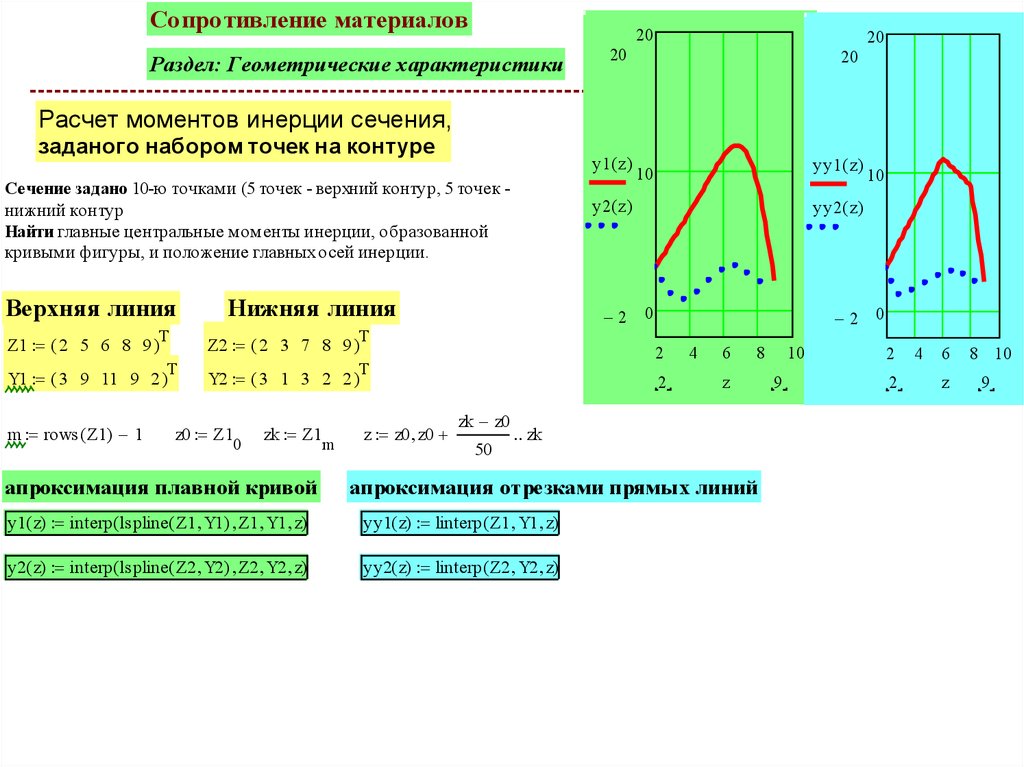
Расчет моментов инерции сечения,
заданого набором точек на контуре
y1( z )
Сечение задано 10-ю точками (5 точек - верхний контур, 5 точек нижний контур
Найти главные центральные моменты инерции, образованной
кривыми фигуры, и положение главных осей инерции.
Верхняя линия
T
Z2 ( 2 3 7 8 9 )
T
m rows ( Z1) 1
Y2 ( 3 1 3 2 2 )
0
zk Z1
апроксимация плавной кривой
m
z z0 z0
10
yy2( z )
0
2
2
T
z0 Z1
y2( z )
2
T
Z1 ( 2 5 6 8 9 )
Y1 ( 3 9 11 9 2 )
Нижняя линия
yy1( z )
10
2
4
6
8
z
10
9
0
2
2
4
6
8 10
z
9
расчет геометрических
характе
следуетДалее
расчетследует
геометрических
характеристик сечения
zk Далее
z0
zk
Для расчета сечения,
характеристик
сечения,
Для расчета характеристик
описанного
отр
50
нижеследующ
нижеследующие
2 выраже
апроксимация отрезками прямых линий
y1( z) interp ( lspline( Z1 Y1) Z1 Y1 z)
yy1( z) linterp ( Z1 Y1 z)
y2( z) interp ( lspline( Z2 Y2) Z2 Y2 z)
yy2( z) linterp ( Z2 Y2 z)

24.

Расчет статических моментов S z, Sy
моментов инерции Jz, Jy, Jzy относительно исходных осей,
а также площади A и координат центра тяжести y c и z c .
Jz
zk
Jy
zk
z0
y1( z )
y1( z )
z0
Jzy
zk
z0
y c
Sz
A
2
Jz 1595
y dy dz
y2( z )
zk
Sz
zk
Sy
zk
z0
2
Jy 1541.669
z dy dz
y2( z )
A
z0
y1( z )
z y d y d z z
Jzy 1433.185
y2( z )
y c 5.57
z0
zc
Sy
A
zc 5.81
y1( z )
y1( z )
y1( z )
1 dy dz
A 42.31
y dy dz
Sz 235.647
z dy dz
Sy 245.736
y2( z )
y2( z )
y2( z )
z z0 z0
Расчет моментов инерции относительно центральных осей,
параллельных исходным
2
Jzc 282.866
Jyc Jy A zc
2
Jyc 114.429
Jzcyc Jzy A zc y c
Jzcyc 64.542
Jzc Jz A y c
zk z0
50
zk

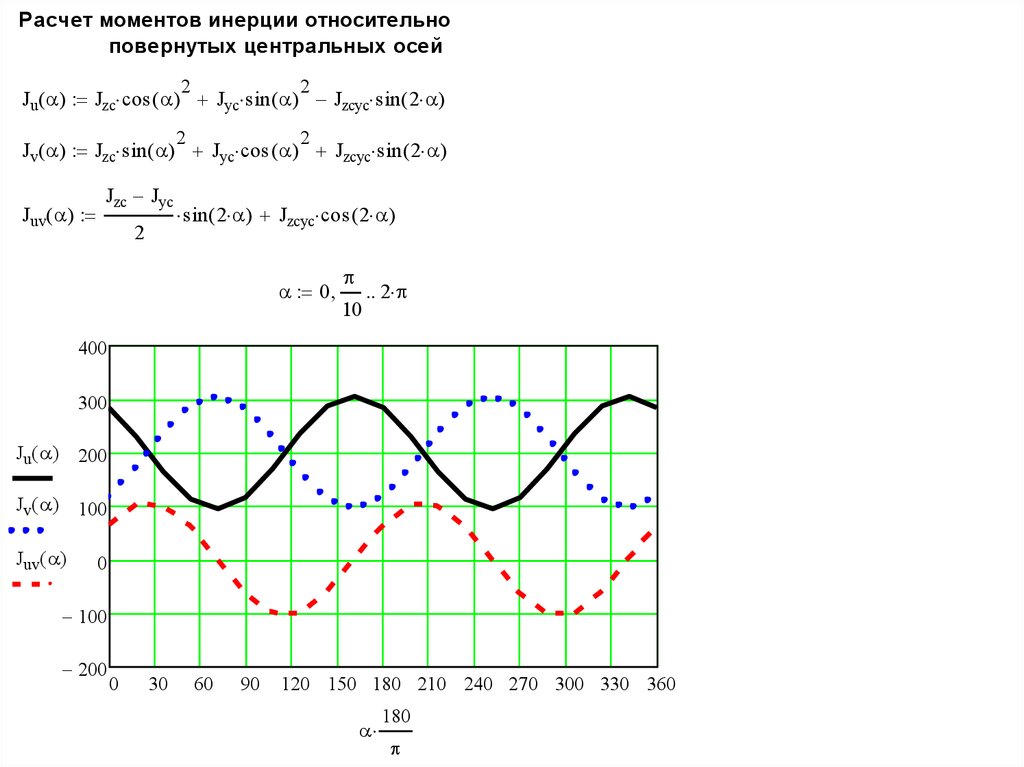
25.

Расчет моментов инерции относительно
повернутых центральных осей
2
2
2
2
Ju( ) Jzc cos ( ) Jyc sin ( ) Jzcyc sin ( 2 )
Jv( ) Jzc sin ( ) Jyc cos ( ) Jzcyc sin ( 2 )
Juv( )
Jzc Jyc
2
sin ( 2 ) Jzcyc cos ( 2 )
0 2
10
400
300
J u( )
200
J v( )
100
Juv( )
0
100
200
0
30
60
90
120 150 180 210 240 270 300 330 360
180

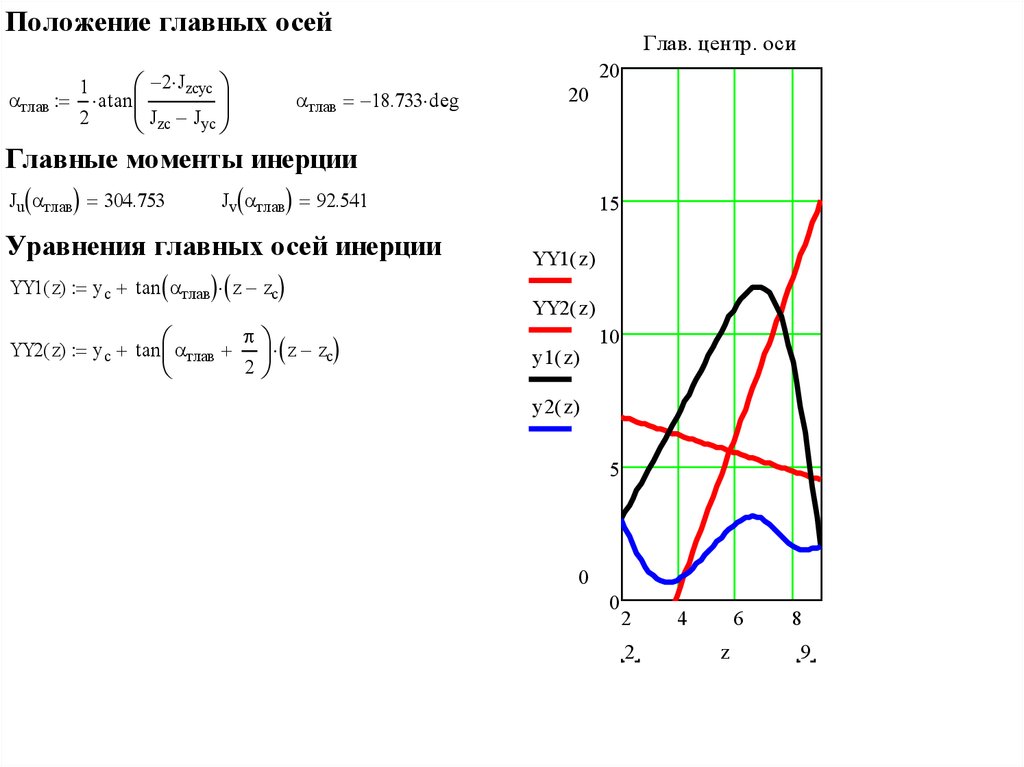
26.

Положение главных осей
Глав. центр. оси
20
2 Jzcyc
глав atan
2
J
J
zc
yc
1
глав 18.733 deg
20
Главные моменты инерции
Ju глав 304.753
Jv глав 92.541
Уравнения главных осей инерции
YY1( z) y c tan глав z zc
YY2( z) y c tan глав
z z
c
2
15
YY1( z )
YY2( z )
y1( z )
10
y2( z )
5
0
0
2
2
4
6
z
8
9

27.

Сопротивление материалов
Раздел: Геометрические характеристики
Расчет геометрических характеристик
составного сечения
ORIGIN 1
Заданное сечение разбито на 7 элементов. Для каждого элемента ввести ширину
элемента b, высоту сечения h, площадь элемента A, координаты центра тяжести Y
и Z в виде элементов вектора для выполнения последующих однотипных
операций. Ввести код элемента K и признак наличия выреза K1. Расшифровка
кодов приведена ниже в тексте программы
Исходные данные
размеры сечений b и h, площади элементов A
T
b ( 5 15 15 7.5 5 3 0 0 )
T
h ( 10 10 5 7.5 5 3 0 0 )
T
A ( 25 75 37.5 88.4 39.3 36 13.3 13.3 )
координаты центра тяжести элементов
T
Y ( 3.33 5 11.67 7.5 7.5 5 6 6 )
T
Z ( 1.67 7.5 10 18.18 15 5 3.66 13.46 )
код элементов K ( 3 1 3 5 2 1 7 7 )T
K1
1 сечение сплошное K1
T
K1 ( 1 1 1 1 1 1 1 1 )
K
1
K
2
K
3
K
4
K
5
K
6
K
7
1 отверстие
n rows ( A )
прямоугольник i 1 n
круг
треугольник Jzy>0
треугольник Jzy<0
полукруг, где d=b - вертикальный размер
полукруг, где d=b - горизонтальный размер
швеллер

28.

Моменты инерции элементов относительно собственных центральных осей
Расчет моментов инерции элементов относительно собственных центральных осей
оформлен в виде подпрограммы. В зависимости от кода К для каждого элемента
введена своя расчетная формула.
i 3
b h
Jz
i
i
12
i
if K
i 4
Jy
1
i
bi 3 hi
i
12
i 4
b
if K
1
Jzy
i
b
if K
i
64
i i 3
2
bi 3 hi
if 3 K 4
i
36
i 4
if K
i
5
i 4
i
if 3 K 4
b
7
if K
i
128
31.2 if K
i
0 if K 7
6
7
0 if K 7
i
i
Координаты центра тяжести сечения
n
n
Aj Yj K1j
Yc
j 1
n
Aj K1j
j 1
Aj Zj K1j
Zc
j 1
n
Aj K1j
j 1
72
bi 2 hi 2
72
0.00686 b 4 if K 5
i i
0.00686 b 4 if K 6
i i
304 if K
2
i
36
b
128
i
64
b h
if K
bi 2 hi 2
Yc 5.22
Zc 10.52
0 otherwise
if K
3
if K
4
i
i

29.

Моменты инерции относительно центральных осей всего сечения
n
J A Y Y 2 K1
c
j j
zj
j
Jz0 7344
J A Z Z 2 K1
c
j j
yj
j
Jy0 13862
Jzyj A j Yj Yc Zj Zc K1j
Jz0
j 1
n
Jy0
j 1
n
Jzy0
j 1
Jzy0 3389
Угол наклона главных осей инерции
глав
1
2
2 Jzy0
Jz0 Jy0
atan
глав 23 deg
Главные центральные моменты инерции
Jmax
Jmin
Jz0 Jy0
2
Jz0 Jy0
2
1
Jz0 Jy0 2 4 Jzy02
Jmax 15305
Jz0 Jy0 2 4 Jzy02
Jmin 5902
2
1
2
С помощью приведенной программы можно
рассчитывать геометрические характеристики
различных сечений. Введите свои исходные
данные и посмотрите результаты расчета. Если
ваше сечение содержит элементы, которых нет
среди указанных семи типов, например, сектор,
сегмент, двутавр, уголок, введите формулы для
них (или численные значения) в
выражения-подпрограммы для моментов инерции.