Подобные треугольники

1.

2.

Пропорциональные отрезки
Отрезки АВ и СD пропорциональны отрезкам
А1В1 и С1D1,
если
=
Пример
2
1
3
1,5
Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1,
=

3.

Понятие пропорциональности вводится и для
большего числа отрезков.
Отрезки
АВ, СD и EF пропорциональны отрезкам А1В1, С1D1 и E1F1,
если
=
=

4.

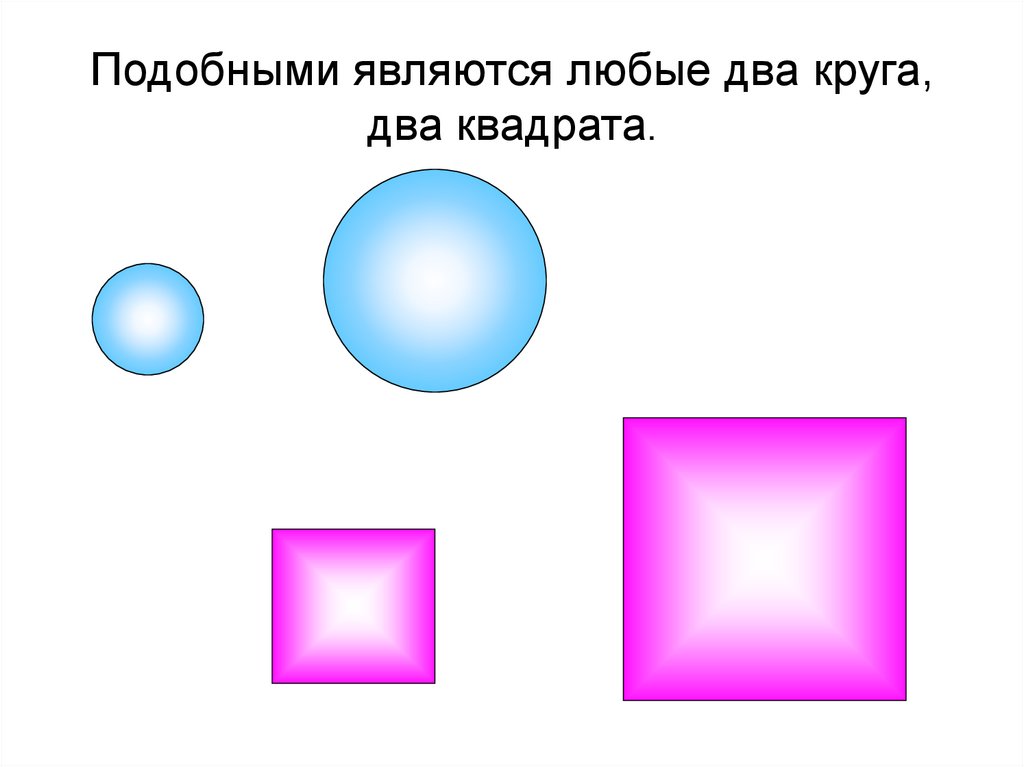
В геометрии фигуры одинаковой формы
принято называть подобными.

5.

Подобными являются любые два круга,
два квадрата.

6.

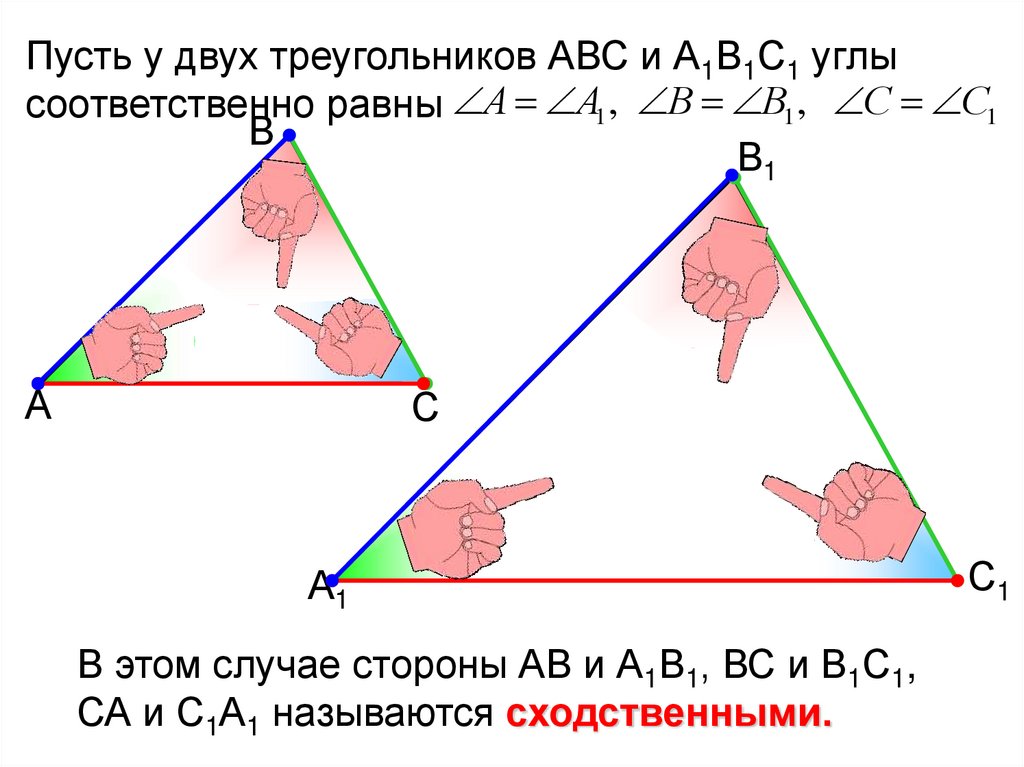
Пусть у двух треугольников АВС и А1В1С1 углы
соответственно равны А А1 , В В1 , С С1
В
В1
А
С
А1
В этом случае стороны АВ и А1В1, ВС и В1С1,
СА и С1А1 называются сходственными.
С1

7.

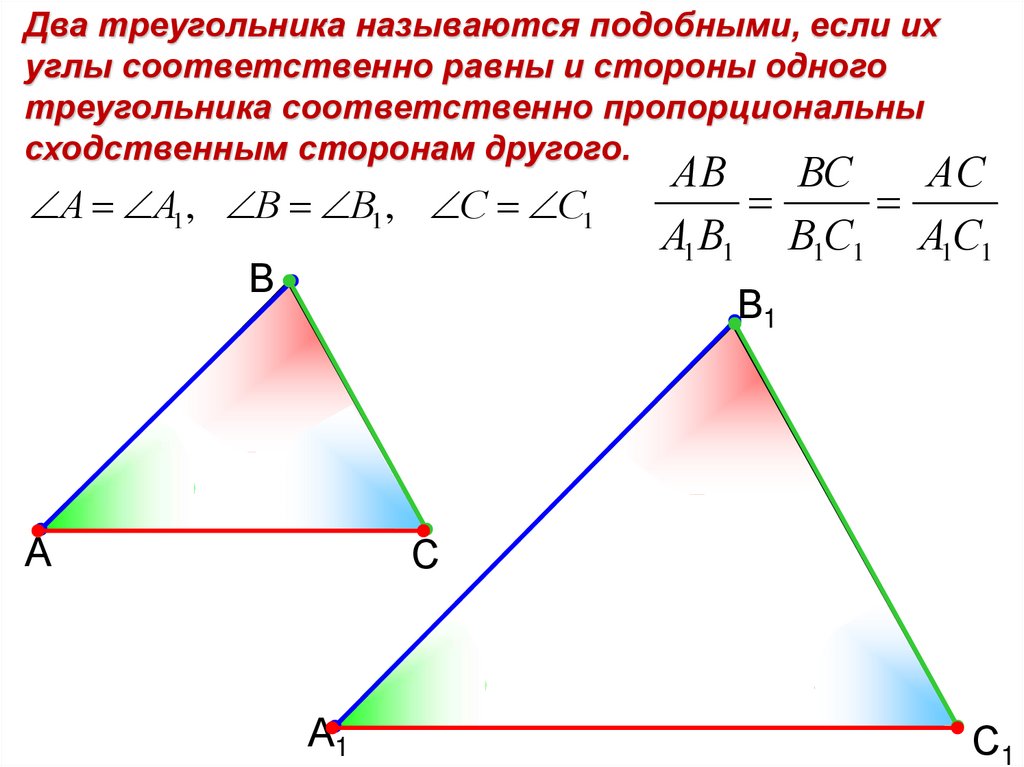
Два треугольника называются подобными, если их
углы соответственно равны и стороны одного
треугольника соответственно пропорциональны
сходственным сторонам другого.
А А1 , В В1 , С С1
В
АВ
ВС
АС
А1 В1 В1С1 А1С1
В1
А
С
А1
С1

8.

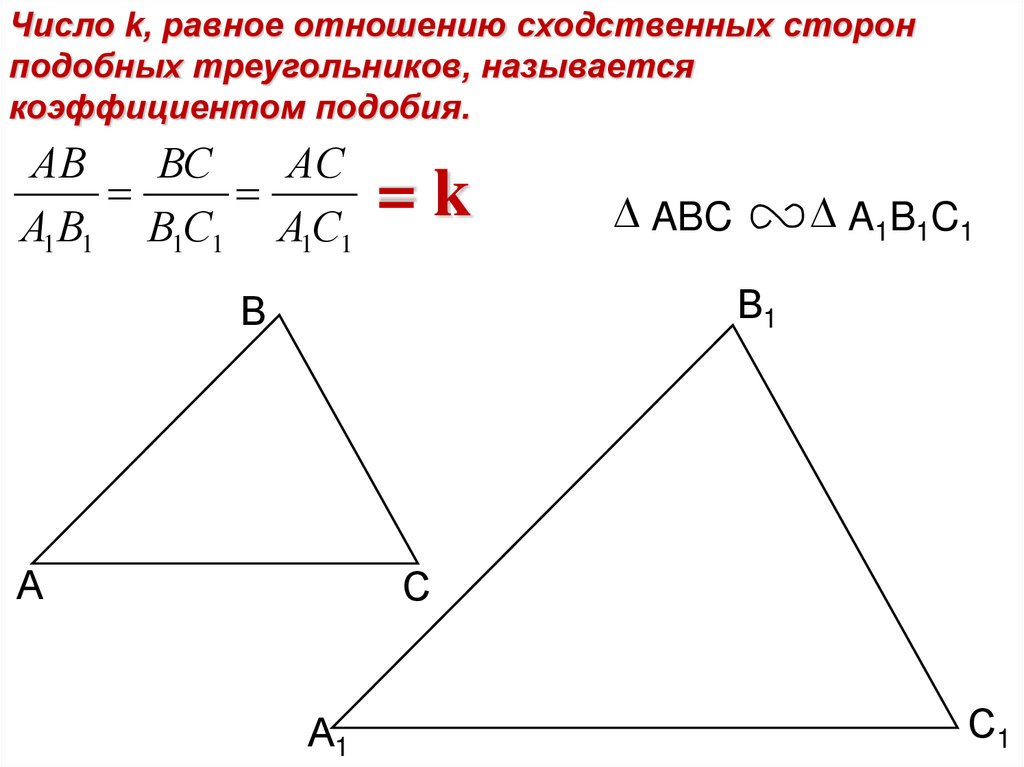
Число k, равное отношению сходственных сторон
подобных треугольников, называется
коэффициентом подобия.
АВ
ВС
АС
=
k
А1 В1 В1С1 А1С1
ABC
A1B1C1
В1
В
А
С
А1
С1

9.

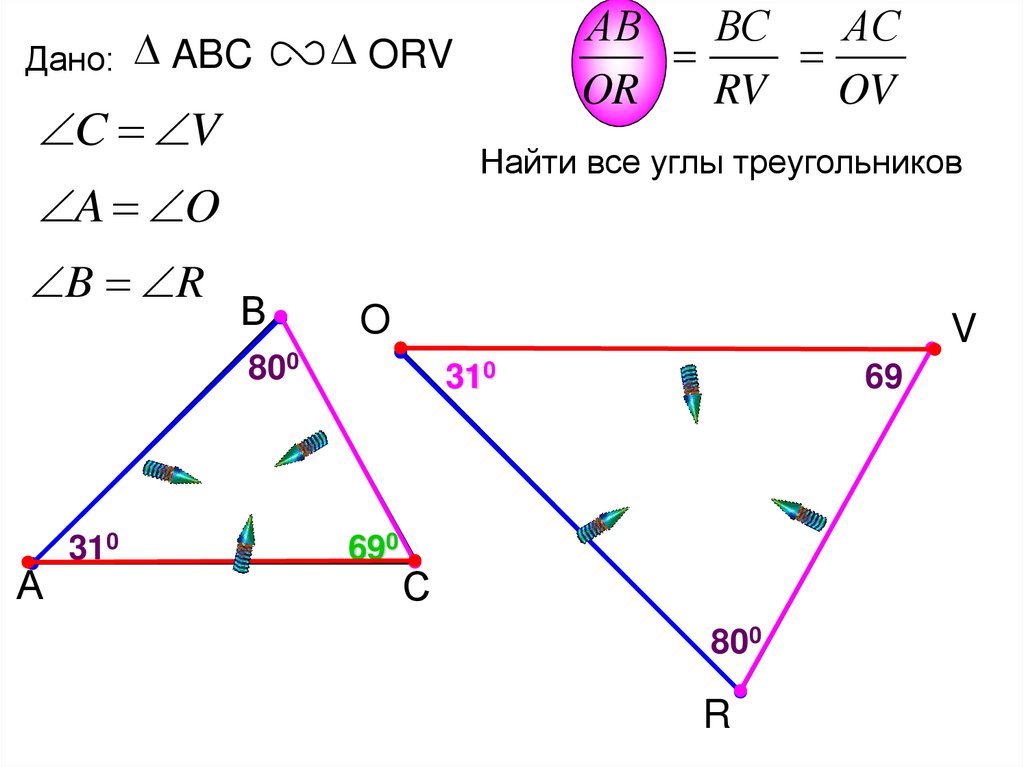
Дано: ABC
ORV
C V
Найти все углы треугольников
A O
B R
В
O
V
800
А
310
АВ
АС
ВС
OR
OV
RV
310
690
69
С
800
R

10.

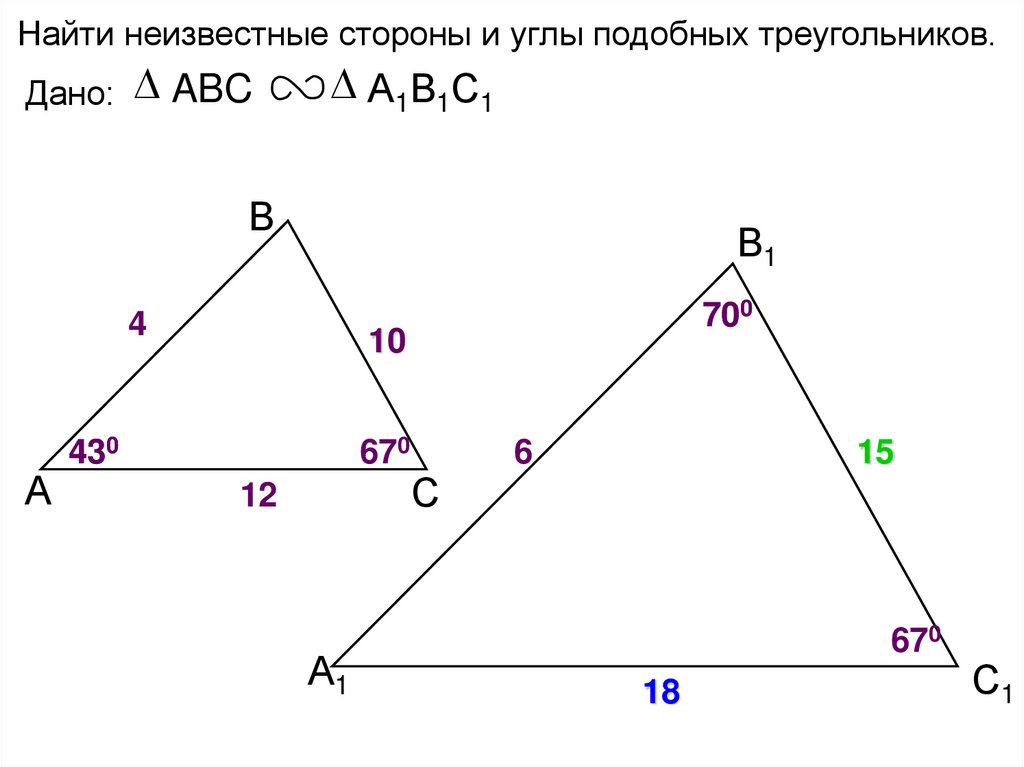
Найти неизвестные стороны и углы подобных треугольников.
Дано: ABC
А1В1С1
В
В1
4
А
700
10
430
670
12
А1
С
6
15
670
18
С1

11.

№547.
A1B1C1
Дано: ABC
Отношение периметров двух
коэффициент подобия
подобных треугольников
равно коэффициенту подобия.
РABC
k
Доказать:
k–
АВ
k
А1 В1
АС
k
А1С1
ВС
k
В1С1
АВ k А1В1
+
РA1B1C1
АС k А1С1
РАВС k А1В1 k A1C1 k B1C1
РАВС k ( А1В1 A1C1 B1C1 )
ВС k В1С1
РАВС k РА1В1С1 : Р А1В1С1
РABC
k
РA1B1C1