Похожие презентации:
Алгебра логики Классы ФАЛ
1. Алгебра логики Классы ФАЛ
Саровский физико-технический институтНационального исследовательского ядерного университета МИФИ
Алгебра логики
Классы ФАЛ
Алексеев В.В.
Саров
2016
1
2. Основные классы ФАЛ
• Имеются функции алгебры логикиq( y1 , y2 ,..., yn ) и f1 , f 2 ,..., f n
и функции f1 , f 2 ,..., f n зависят от одних и
тех же аргументов x1 , x2 ,....xm .
Функцию
h( x1 , x2 ,..., xm ) q[ f1( x1 ,...xm ),...., f n ( x1 ,.....xm )]
называют суперпозицией функций q и
f1 , f 2 ,..., f n
2
3.
Определение: Класс А называетсязамкнутым, если для всяких функций
q( y1 ,....yn ) и f1 , f 2 ,..., f n из А их
cуперпозиция q( f1 ,.... f n ) содержится в А.
q( y1 , yn ) A и f i A | q( f1 , f 2 f n ) A
1. Класс функций, сохраняющих
константу нуль, т.е. таких функций, для
которых имеет место f(0,0,0,...,0)=0.
Обозначим этот класс 0 .
Теорема. Класс функций, сохраняющих
константу нуля, есть замкнутый класс.
3
4.
2. Класс функций, сохраняющихконстанту единица определен
как класс функций, для которых
f(1,1,...,1)=1. Обозначим этот класс
как 1.
Теорема. Класс функций,
сохраняющих константу единицы
есть замкнутый класс.
4
5. Принципы и законы двойственности АЛ
• Принципы двойственности можнозаписать следующим образом: Если
имеет место тождество
f ({x},0,1 / V,&) g({x},0,1 / V,&)
где {x} x1 , x 2 ,..., x n, то справедливо
также тождество
f ({x},1,0/&, V) g({x},1,0/&, V)
• Два тождества, связанные между собой
таким образом, являются двойственными.
5
6.
• Закон двойственности, установленныйШенноном имеет вид:
f ( x / V ,&) f ( x / &,V ), где x = x1 , x2 , xn
x = x1 , x2 , xn .
• На основании закона двойственности
легко показать, что
n
n
i 1
i 1
V xi & xi :
n
n
i=1
i 1
& xi V xi
6
7.
• Определение Функция f ( x1 , x2 , xn )называется самодвойственной, если
она совпадает с двойственной себе
функцией, т.е. имеет место равенство
f ( x1 , x2 , xn ) f ( x1 , x2 , xn )
7
8.
3. Класс самодвойственных функцийобозначим символом S. (Функция
f ( x1 , x2 , xn ) называется самодвойственной,
если она совпадает с двойственной себе
функцией, т.е. имеет место равенство
f ( x1 , x2 xn ) f ( x1 , x 2 x n )
Теорема. Класс самодвойственных ФАЛ есть
замкнутый класс.
8
9.
4. Класс линейных функций обозначимбуквой L. (Функция f ( x 1 , x 2 , x n )
называется линейной, если она
представима в следующем виде:
f c 0 c1 x 1 c n x n
Теорема. Класс линейных ФАЛ есть
замкнутый класс.
9
10.
5. Класс монотонных функций (М)Набор значений аргументов X̂1 x11 ,x12 , x1n
не меньше набора значений аргументов
X̂ 2 x12 ,x22 , xn2 если между всеми
компонентами наборов установлено
соотношение 1
2
xi xi
( i 1,2 , n )
• Определение. Функция f ( x 1 , x 2 , x n )
называется монотонной, если для двух
1 и X
2 таких, что X X
наборов X
2
1
имеет место равенство
1 ) f (X
2)
f (X
10
11.
• Теорема. Класс монотонных функцийесть замкнутый класс.
• Определение. Функция f ( x 1 , x 2 , x n )
называется симметричной, если она не
изменяется при произвольной
перенумерации аргументов
f ( x1 , x2 , xn ) f ( y1 , y2 , yn )
где ( y 1 , y 2 , y n ) - любая перестановка
аргументов ( x 1 , x 2 , x n ) .
11
12. Полные системы ФАЛ
• Определение. Система функций алгебрылогики f1 ,f2 , fn называется полной в
классе R, если любая функция ,
принадлежащая R, может быть
представлена суперпозицией функций
f1 ,f2 , fn
• Определение. Система функций
f1 , f2 , fn , являющаяся полной в классе
R, называется базисом.
12
13.
• Или: Базисом называется полнаясистема ФАЛ, с помощью которой
любая ФАЛ может быть представлена
суперпозицией исходных функций.
• Определение. Минимальным базисом
называется такой базис, для которого
удаление хотя бы одной из функций f i ,
образующих этот базис, превращает
систему функций f1 , f 2 , f n в
неполную.
13
14.
• Теорема Функция Шеффера естьбазис.
• Теорема Функция Пирса (Вебба) есть
базис.
• Теорема Поста-Яблонского (без
доказательства) Для того чтобы
система ФАЛ была полной, необходимо
и достаточно, чтобы она содержала
хотя бы одну функцию:
не сохраняющую нуль;
не сохраняющую единицу;
не являющейся линейной;
не являющейся монотонной;
не являющейся самодвойственной.
14
15. Минимизация ФАЛ
• Минимальная форма представления ФАЛесть такая форма представления, которая
содержит минимальное количество термов
и переменных в термах. Минимальная
форма представления ФАЛ не допускает
никаких упрощений.
1
2
n
• Определение. Конъюнкция x 1 x 2 x n
называется элементарной, если в этой
конъюнкции каждая переменная
15
встречается не более одного раза.
16.
• Определение. Дизъюнкцияэлементарных конъюнкций называется
дизьюнктивной нормальной формой (ДНФ
или НДФ).
• Определение. Длиной ДНФ называется
число элементарных конъюнкций,
образующих эту ДНФ.
• Определение. Дизъюнктивная
нормальная форма, имеющая
наименьшую длину по сравнению со
всеми другими ДНФ, эквивалентными
данной функции, называется кратчайшей
ДНФ
16
17.
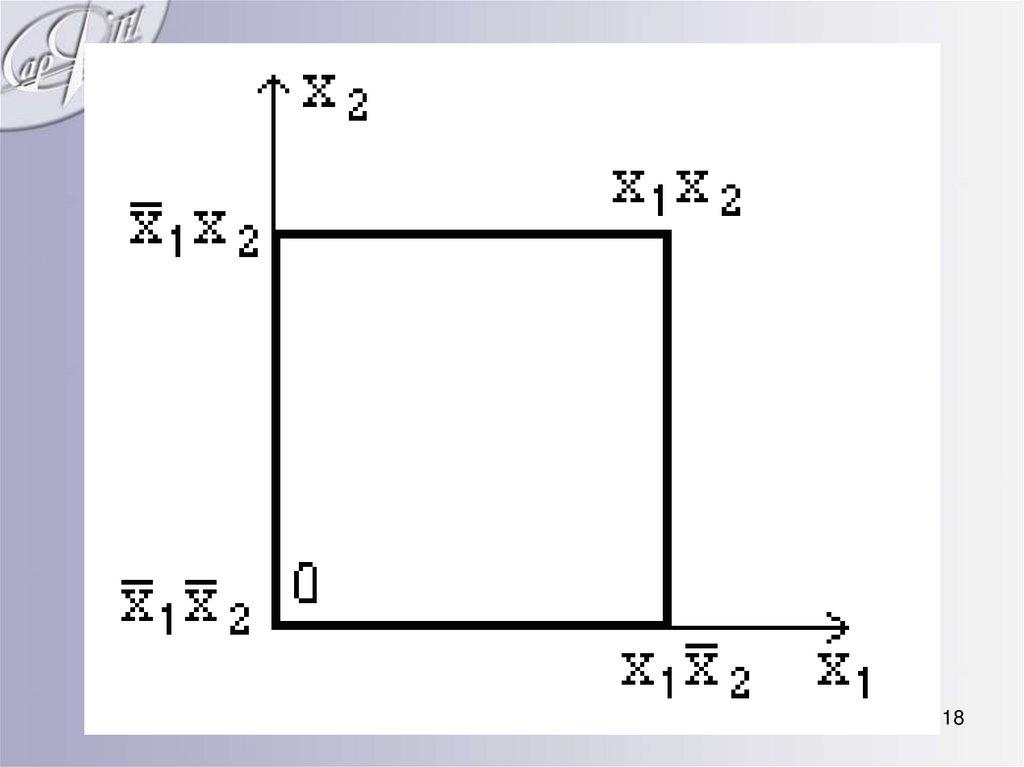
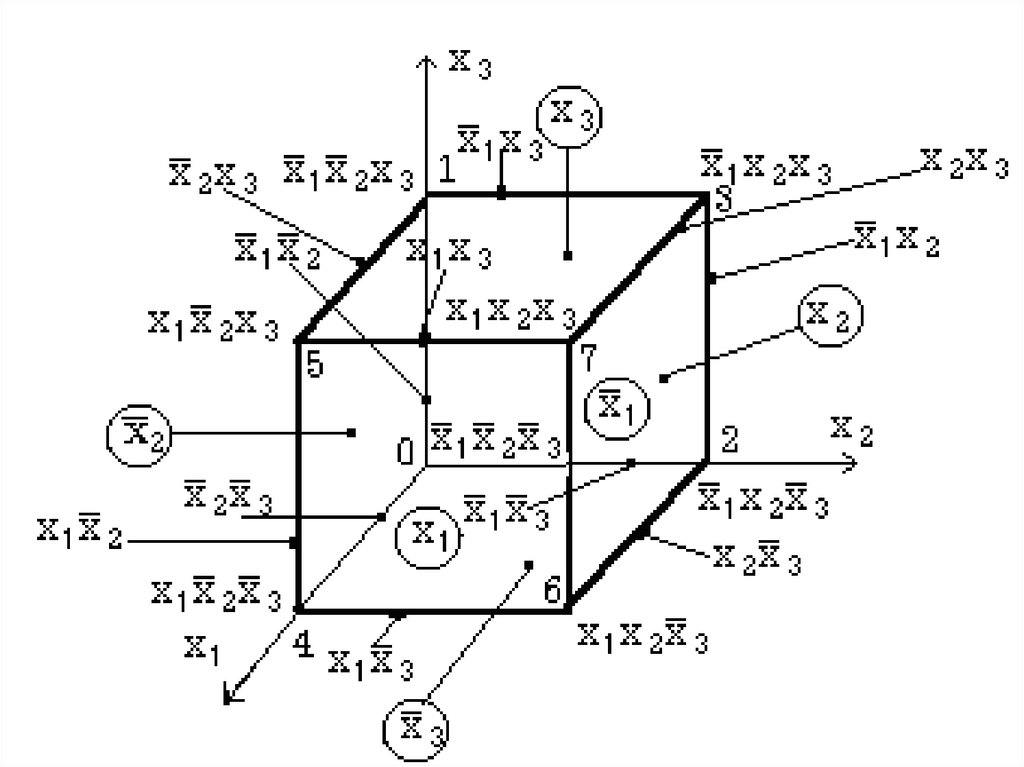
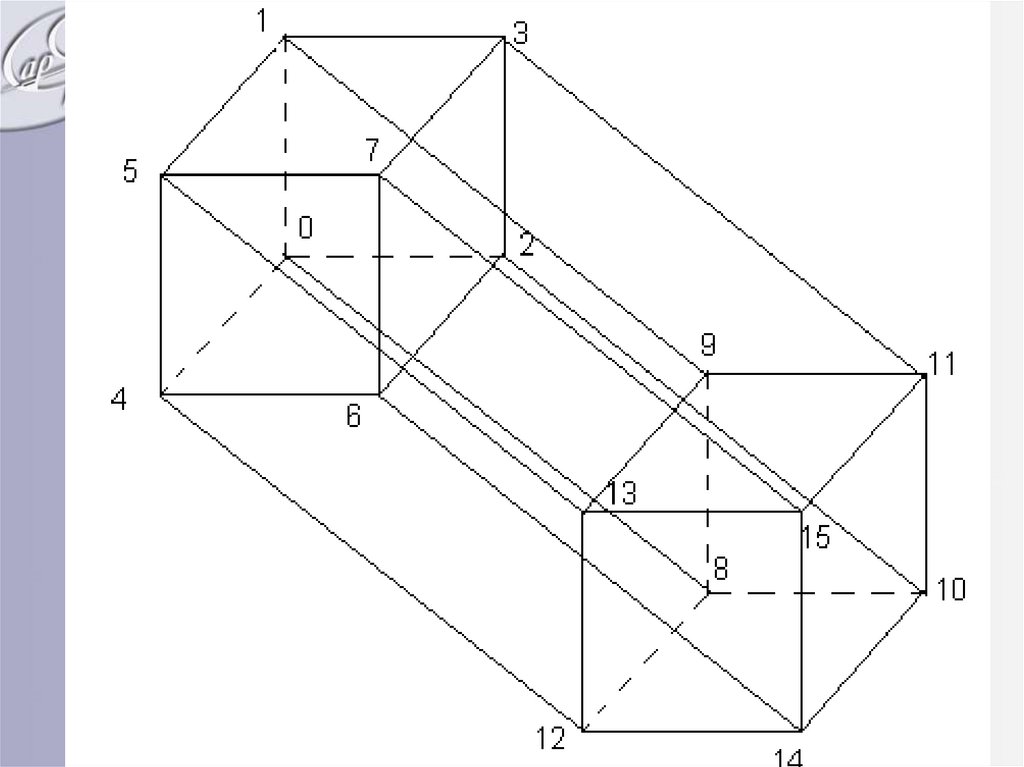
Числовое и геометрическоепредставление ФАЛ.
17
18.
1819.
1920.
2021. Метод неопределенных коэффициентов
• Описываемый здесь метод может бытьприменим для минимизации ФАЛ от
любого числа аргументов, однако для
простоты изложения и большой
наглядности его рассмотрение
произведем на примере минимизации
функции, зависящей от трех
переменных f ( x 1 , x 2 , x 3 )
21
22.
f ( x1 , x2 , x3 ) K x K x K x K x1
1 1
0
1 1
1
2 2
0
2 2
K x K x K xx K xx
1
3 3
0
3 3
11
12 1 2
10
12 1 2
K xx K xx K xx K xx
01
12 1 2
00
12 1 2
11
13 1 3
10
13 1 3
K xx K xx K x x K x x
01
13 1 3
00
13 1 3
11
23 2 3
10
23 2 3
K x x K x x K xx x
01
23 2 3
000
123 1 2 3
K
101
123 1 2 3
xx x K
011
123 1 2 3
K
111
123 1 2 3
xx x K xx x K
110
123 1 2 3
K
00
23 2 3
xx x
xx x
100
123 1 2 3
xx x K
010
123 1 2 3
xx x
001
123 1 2 3
22
23.
• Если теперь задавать всевозможныенаборы значений аргументов ( x1 , x2 , x3 ) ,
и приравнять после этого выражение
( отбрасывая нулевые конъюнкции)
значению функции на выбранных
наборах, то получим систему
уравнений:
23
24.
0000
00
000
K 10 K 02 K 03 K 12
K 13 K 23 K 123 f 0 ( 0,0,0)
0
0
1
00
01
01
001
K
K
K
K
K
K
K
1
2
3
12
13
23
123 f1 ( 0,0,1)
0
1
0
01
00
10
010
K 1 K 2 K 3 K 12 K 13 K 23 K123 f 2 ( 0,1,0)
K 0 K 1 K 1 K 01 K 01 K 11 K 011 f ( 0,1,1)
1
2
3
12
13
23
123
3
1
0
0
10
11
00
100
K 1 K 2 K 3 K 12 K 13 K 23 K 123 f 4 (1,0,0)
1
0
1
10
11
01
101
K
K
K
K
K
K
K
f
(
1
,
0
,
1
)
1
2
3
12
13
23
123
5
K 1 K 1 K 0 K 11 K 10 K 10 K 110 f (1,1,0)
2
3
12
13
23
123
6
1
11
11
111
K 11 K 12 K 13 K 11
K
K
K
12
13
23
123 f 7 (1,1,1)
24
25. Алгоритм нахождения неопределенных коэффициентов:
1. Выбрать очередную строку, в которой f i =0. Всекоэффициенты этой строки приравнять нулю;
2. Если все нулевые строки просмотрены, то
перейти к п.3, если нет, то к п.1;
3. Просмотреть строки, в которых =1, и
fi
вычеркнуть из них все коэффициенты,
встречающиеся в строках, где =0;
fi
4. Переписать все модифицированные
уравнения;
5. Выбрать очередную строку
=1 и вычеркнуть
fi
максимально возможное количество
коэффициентов так, чтобы ранг остающихся
членов был минимальным.
25
26. Пример. Минимизировать функцию:
f (x 1 , x 2 , x 3 ) V(1,3,4,6)1
• Запишем данную функцию в
дизъюнктивной форме:
f ( x1 , x2 , x3 ) ( 1,3,4,6 ) x1 x2 x3
1
x1 x2 x3 x1 x2 x3 x1 x2 x3
• Составим систему уравнений:
26
27.
0000
00
000
K 10 K 02 K 03 K12
K13 K 23 K123 0
0
0
1
00
01
01
001
K 1 K 2 K 3 K 12 K 13 K 23 K 123 1
0
1
0
01
00
10
010
K
K
K
K
K
K
K
0
1
2
3
12
13
23
123
K 0 K 1 K 1 K 01 K 01 K 11 K 011 1
1
2
3
12
13
23
123
1
0
0
10
10
00
100
K 1 K 2 K 3 K 12 K13 K 23 K 123 1
1
0
1
10
11
01
101
K
K
K
K
K
K
K
0
1
2
3
12
13
23
123
K 1 K 1 K 0 K 11 K10 K 10 K 110 1
1
2
3
12
13
23
123
11
11
111
K 11 K 12 K 13 K11
12 K 13 K 23 K 123 0
27
28. Отсюда вытекает, что
K K K KK
0
1
0
2
0
3
00
23
K
K
K K
1
3
K
01
23
00
123
10
12
01
12
00
12
K
00
13
K K
1
2
1
1
K K K
11
12
11
13
K K
K
11
23
010
123
101
123
10
23
K
111
123
0.
• После вычеркивания нулевых
коэффициентов уравнения принимают
вид:
28
29.
01001
K13
K123 1
01
011
K
K
13
123 1
10
100
K13 K123 1
10
110
K
K
123 1
13
• И вполне очевидно, что из этих
уравнений следует:
01
K13 1
10
K13 1
f (x 1 , x 2 , x 3 ) x1 x 3 x 1 x 3 x 1 x 3
29
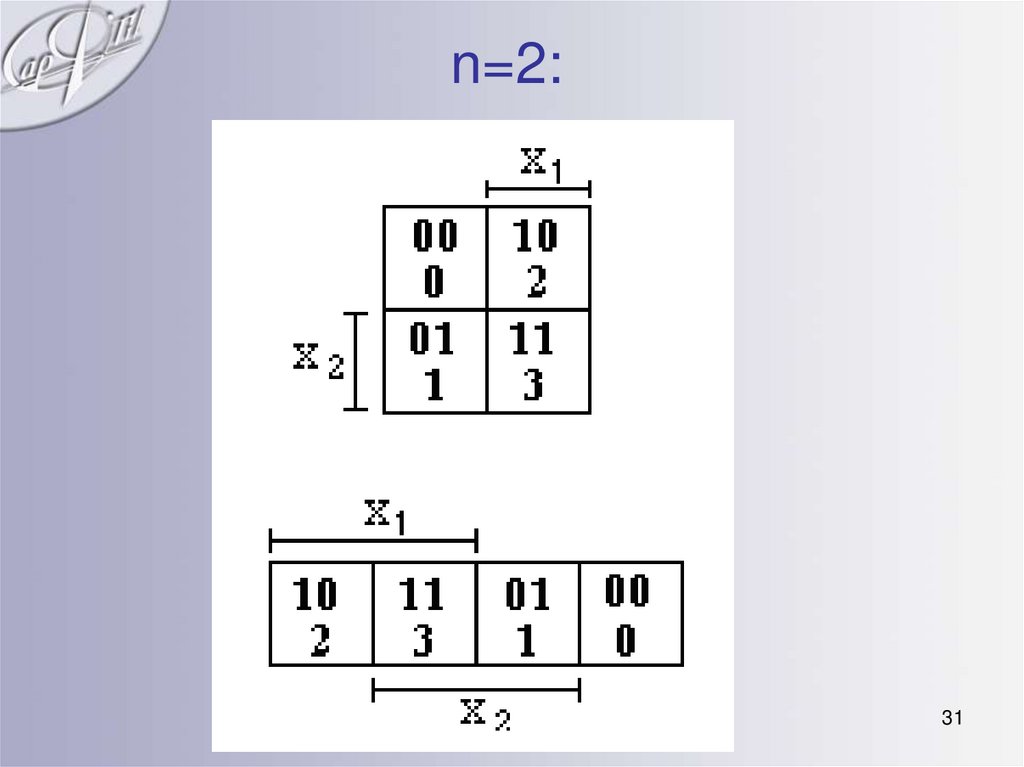
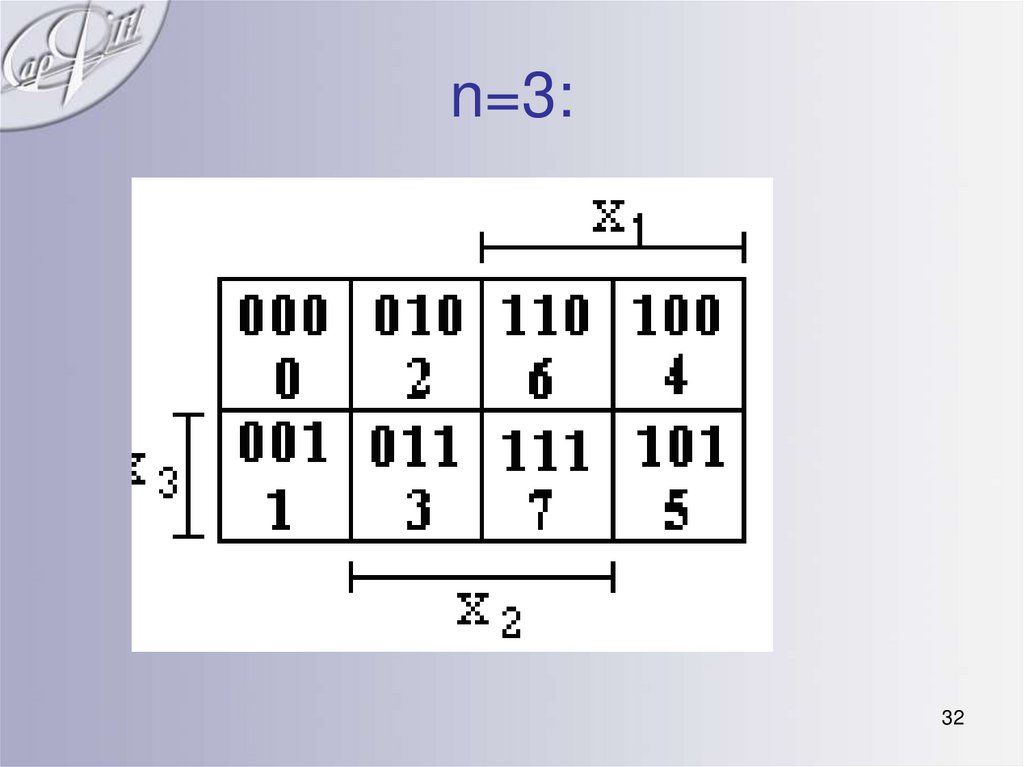
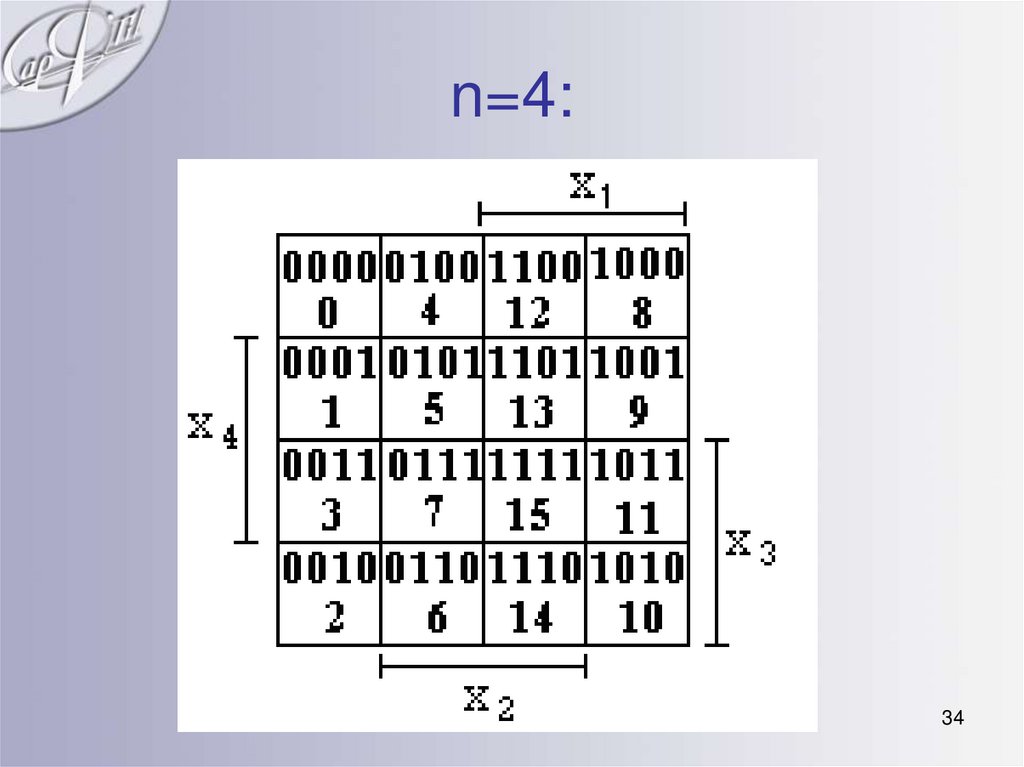
30. Метод минимизирующих карт (Карты Карно)
• Карта Карно заполняется также, кактаблица истинности: В каждой клетке,
соответствующей набору, проставляется
значение функции. Переменные
размещаются на карте так, что при
переходе из одной клетки в любую
соседнюю, должна изменяться только одна
переменная. Нижний ряд карты следует
рассматривать как примыкающий к
верхнему ряду, а левый ряд - к правому.
30
31. n=2:
3132. n=3:
3233.
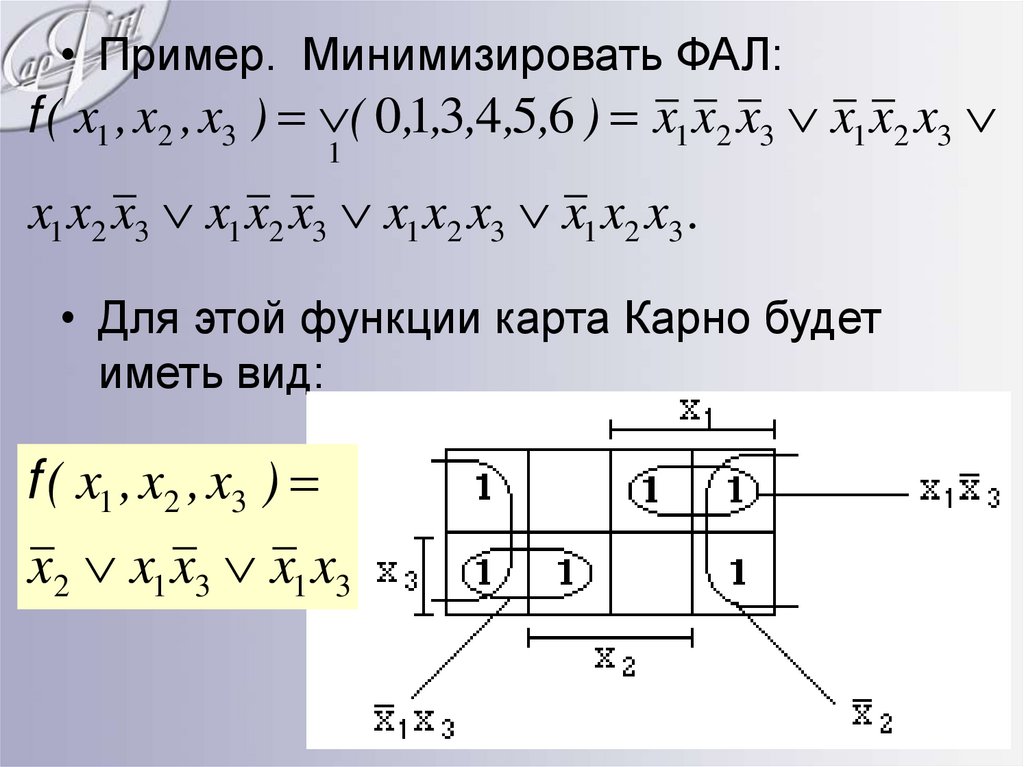
• Пример. Минимизировать ФАЛ:f ( x1 , x2 , x3 ) ( 0,1,3,4,5,6 ) x1 x2 x3 x1 x2 x3
1
x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
• Для этой функции карта Карно будет
иметь вид:
f ( x1 , x2 , x3 )
x2 x1 x3 x1 x3
33
34. n=4:
3435.
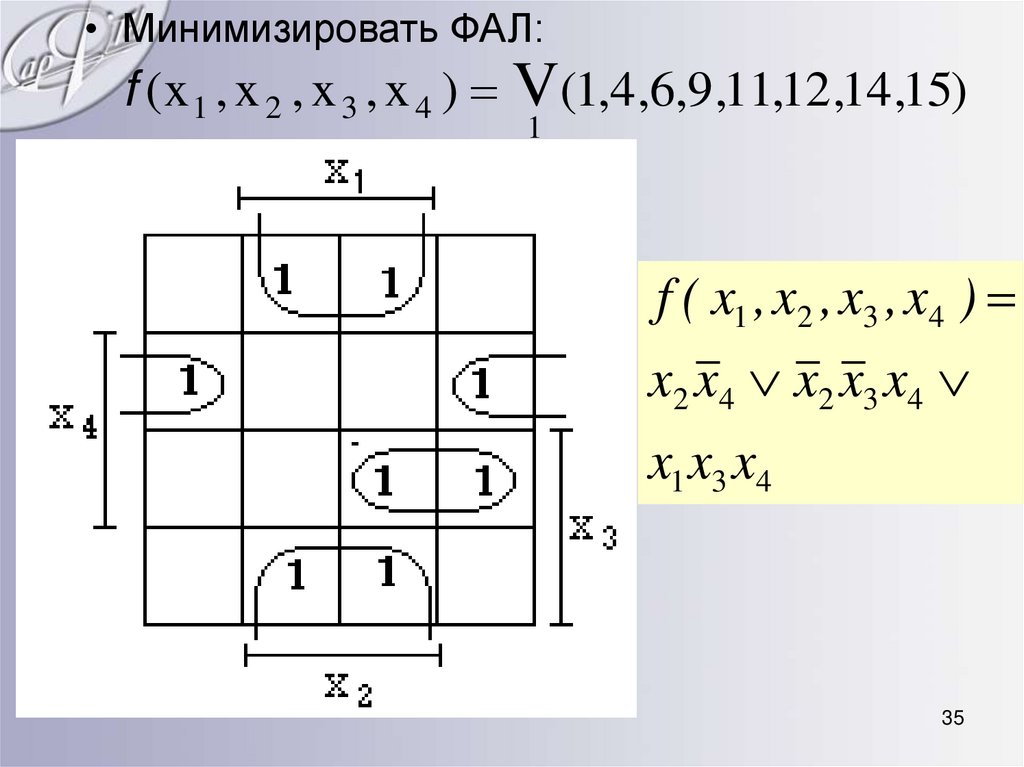
• Минимизировать ФАЛ:f ( x 1 , x 2 , x 3 , x 4 ) V(1,4 ,6,9 ,11,12 ,14 ,15)
1
f ( x1 , x2 , x3 , x4 )
x2 x4 x2 x3 x4
x1 x3 x4
35
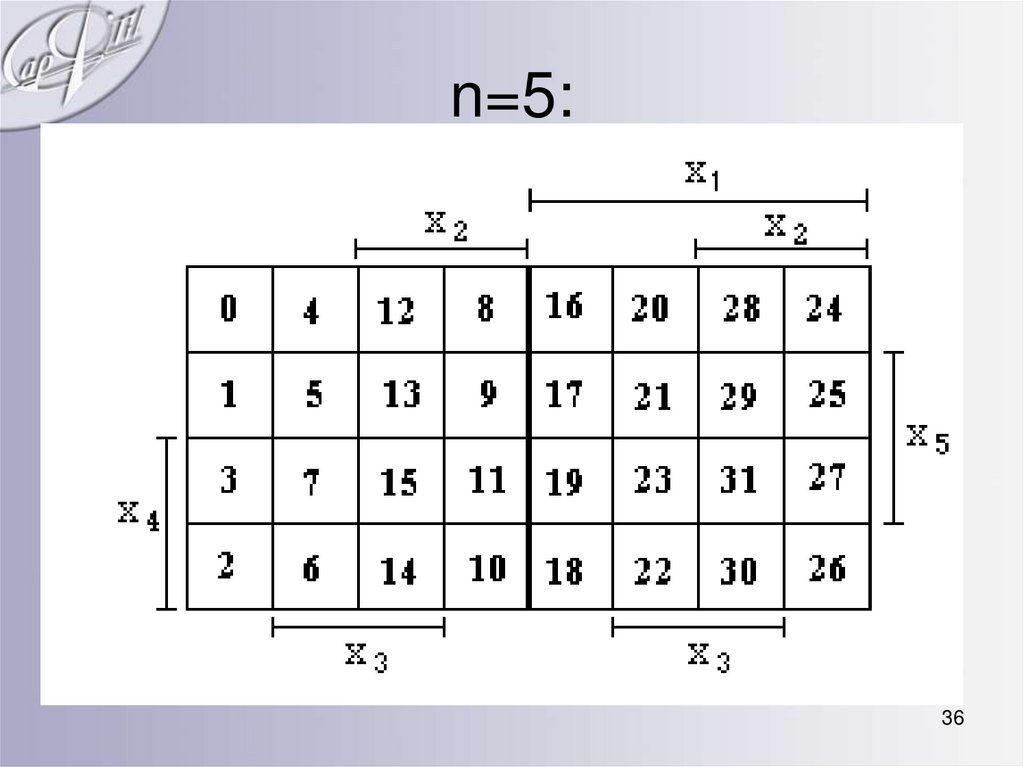
36. n=5:
3637.
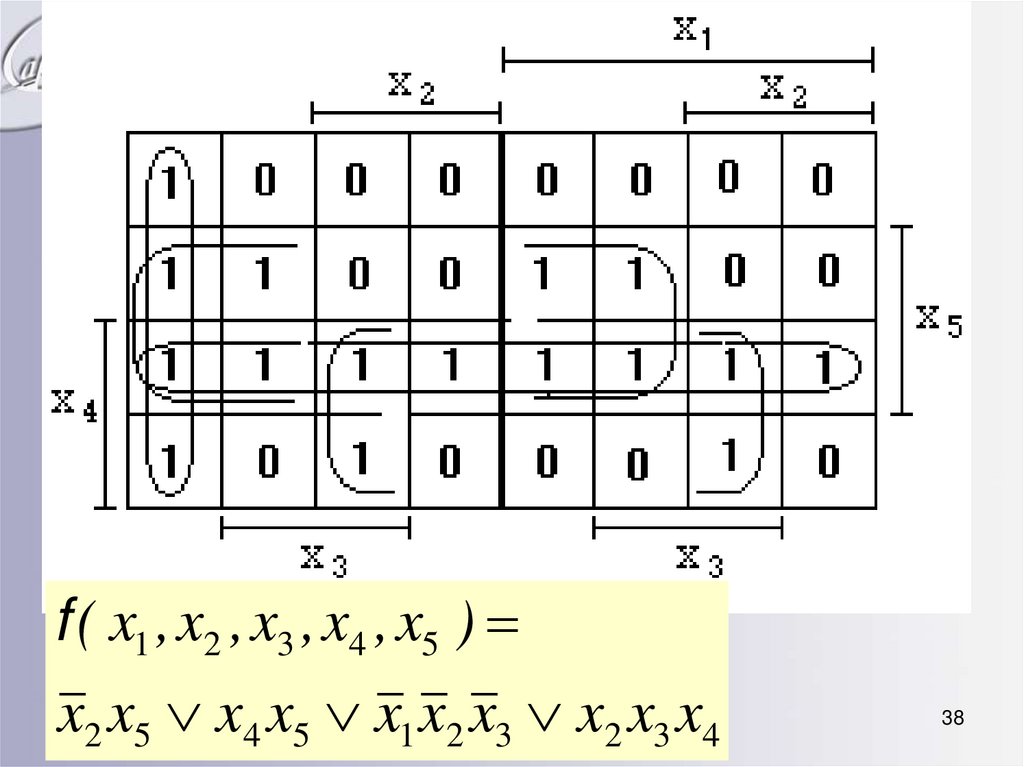
• Пример. Минимизировать ФАЛ:f ( x1 , x2 , x3 , x4 , x5 )
(
0
,
1
,
2
,
3
,
5
,
7
,
11
,
14
,
15
,
17
,
19
,
21
,
23
,
27630
,
31
)
1
37
38.
f ( x1 , x2 , x3 , x4 , x5 )x2 x5 x4 x5 x1 x2 x3 x2 x3 x4
38
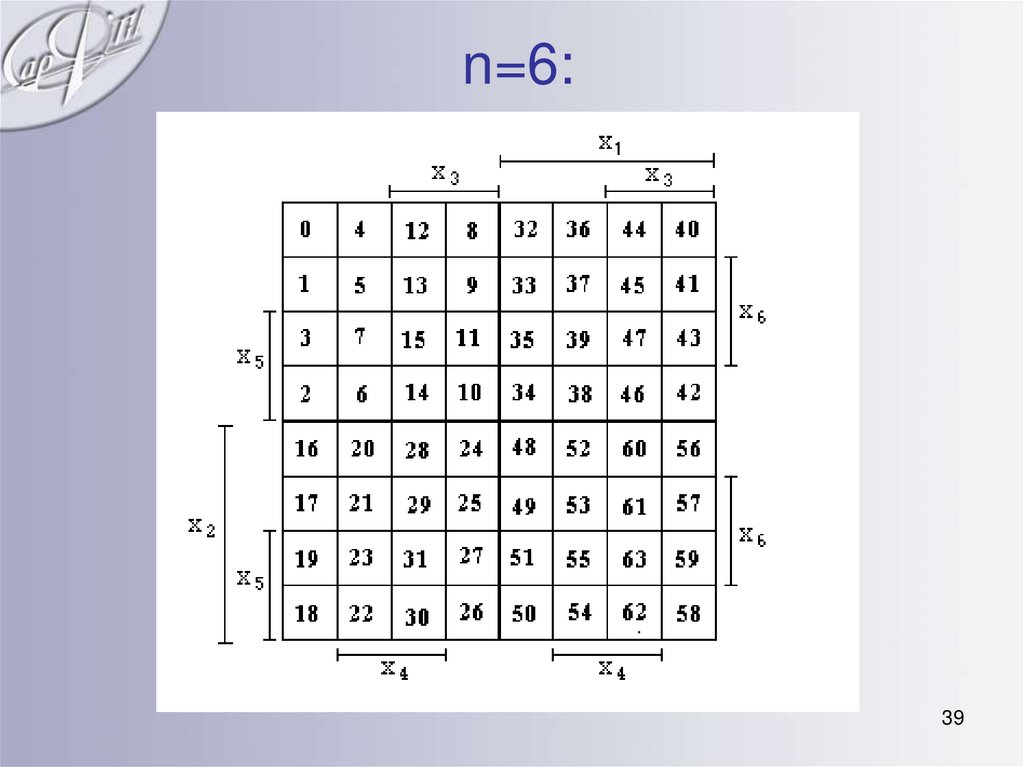
39. n=6:
3940.
• Пример. Минимизировать ФАЛ:f ( x1 , x2 , x3 , x4 , x5 , x6 )
( 0 ,1,5,7 ,13,15,16 ,17 ,21,
1
23,26 ,29 ,31,32 ,33,37 ,39 ,
45,47 ,48,49 ,50 )
• Заполняя карту Карно для n=6
получаем:
40
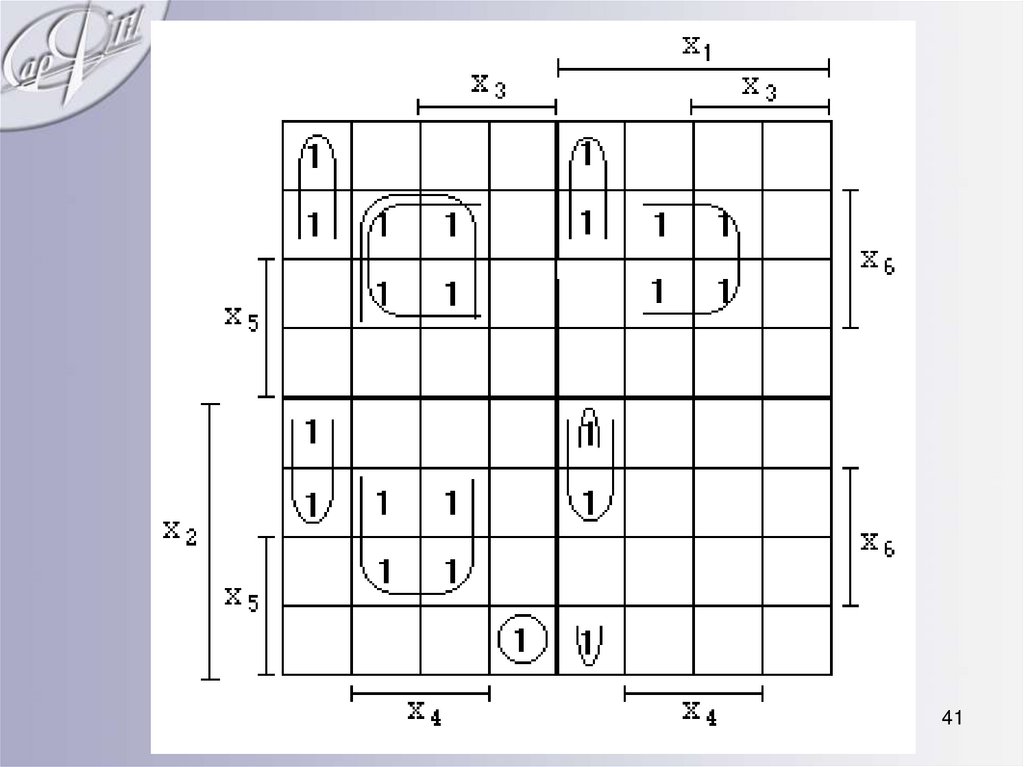
41.
4142.
• Результат минимизации будетпредставлен в данном случае как:
f x2 x4 x6 x1 x4 x6 x3 x4 x5
x1 x2 x3 x4 x6 x1 x2 x3 x4 x5 x6
42
43.
• Карты Карно используют и дляполучения минимальных КНФ. Это
вытекает из принципа двойственности и
законов двойственности. Покажем это
на примере.
• Пусть имеем ФАЛ
f ( x1 , x2 , x3 , x4 )
( 3,5,7 ,11,12,13,14,15 )
1
43
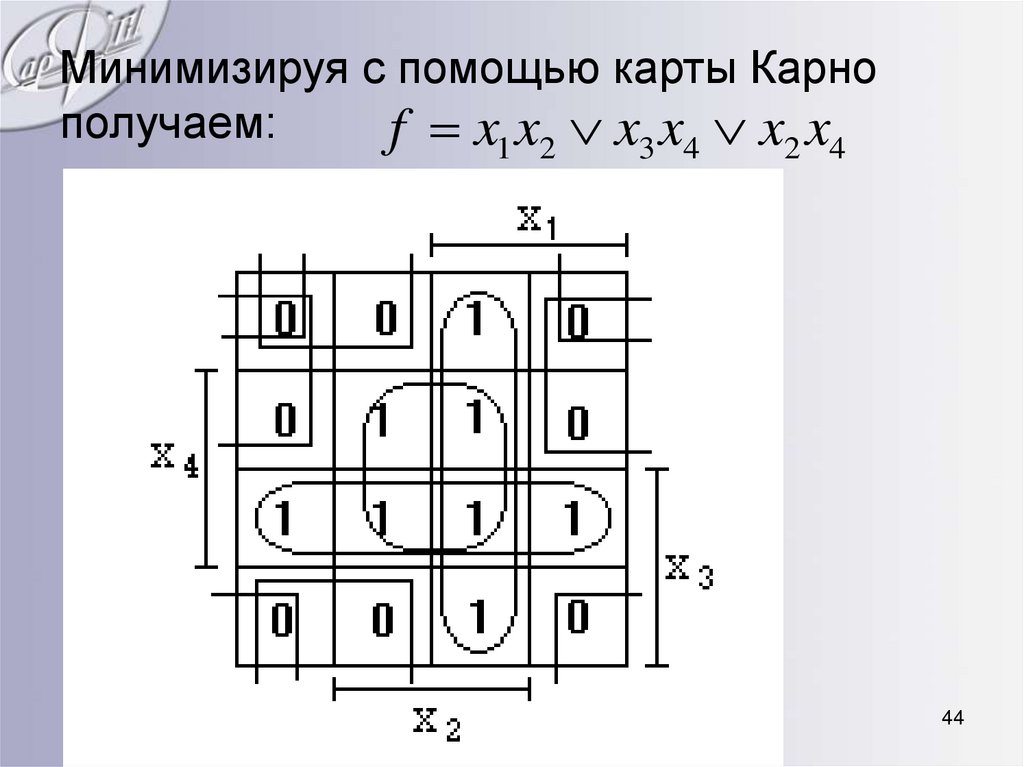
44. Минимизируя с помощью карты Карно получаем:
f x1 x2 x3 x4 x2 x444
45. Тогда имеет место в данном случае следующее соотношение:
f ( x1 , x2 , x3 , x4 ) x2 x3 x1 x4 x2 x4• откуда на основании двойственности
получаем:
f ( x1 , x2 , x3 , x4 )
( x2 x3 ) ( x1 x4 ) ( x2 x4 )
45


















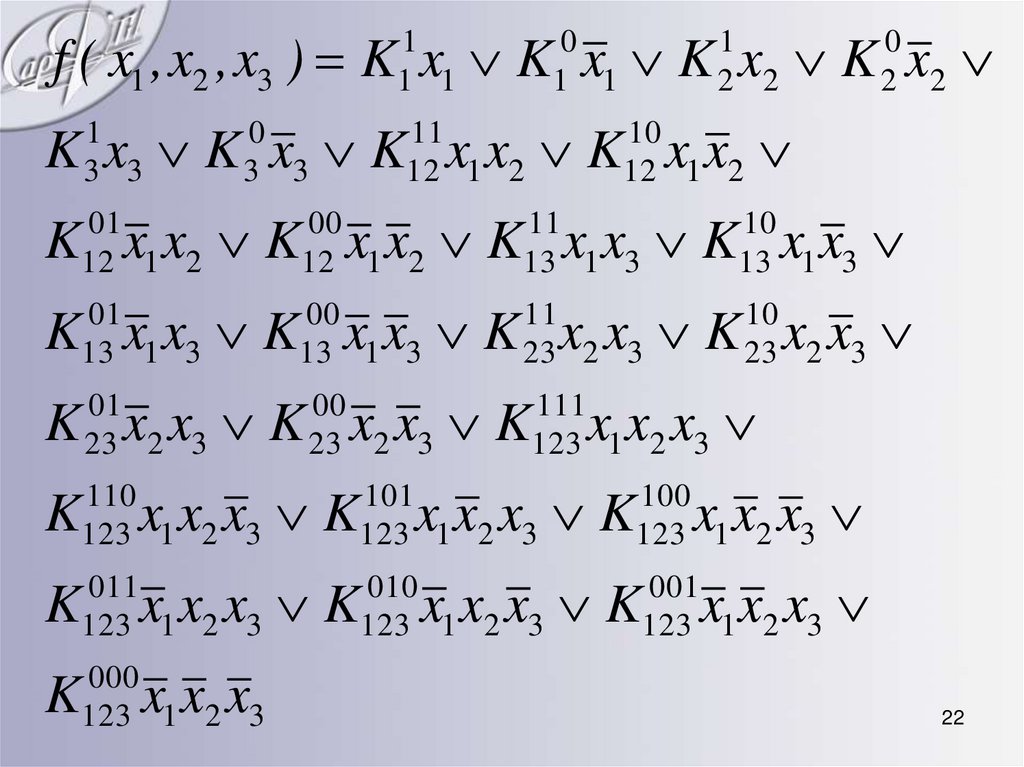













 Математика
Математика








