«Конструирование привода с одноступенчатым редуктором

1.

Курсовое проектирование по дисциплине
«Детали машин и основы конструирования»
Тема проекта: «Конструирование привода с
одноступенчатым редуктором»

2.

Необходимая литература:
Авторы: Г. П. Здор, А. В. Бородин, Д. В. Тарута
Название: Проектирование механического привода с цилиндрическим
одноступенчатым редуктором
Методические указания
1.
Авторы: Г. П. Здор, А. В. Бородин
Название: Проектирование электромеханического привода. Расчет и
конструирование ременных передач (Часть 1)
Методические указания
2.
3.
Авторы: П. Ф. Дунаев, О. П. Леликов
Название: Конструирование узлов и деталей машин
Учебник
2

3.

Задание на курсовой проект
Следует обратить внимание на пункты 2, 3, 4, 5, 6, 9 исходных данных и пункт 3 объема
проектирования. Для каждого обучающегося приводятся свои данные.
3

4.

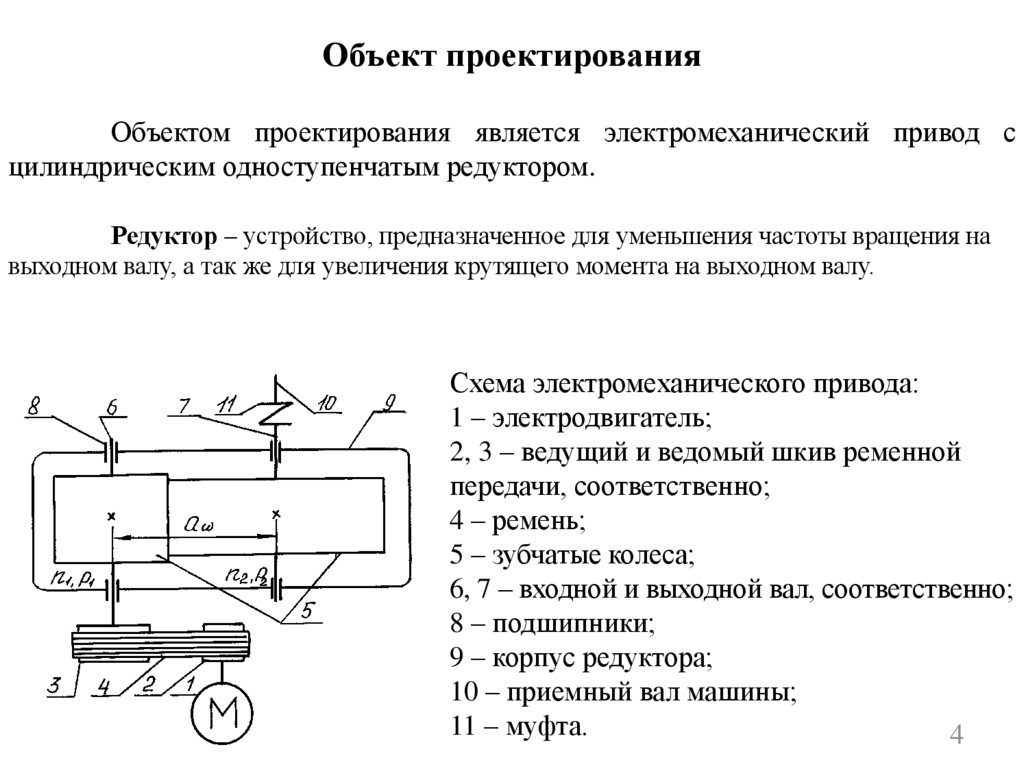
Объект проектирования
Объектом проектирования является электромеханический привод с
цилиндрическим одноступенчатым редуктором.
Редуктор – устройство, предназначенное для уменьшения частоты вращения на
выходном валу, а так же для увеличения крутящего момента на выходном валу.
Схема электромеханического привода:
1 – электродвигатель;
2, 3 – ведущий и ведомый шкив ременной
передачи, соответственно;
4 – ремень;
5 – зубчатые колеса;
6, 7 – входной и выходной вал, соответственно;
8 – подшипники;
9 – корпус редуктора;
10 – приемный вал машины;
11 – муфта.
4

5.

1. Кинематический расчет и выбор электродвигателя
1.1 Определение потребной мощности и выбор электродвигателя
Общий КПД привода, р ц п2
(1.1)
где р = 0,96 – КПД плоскоременной передачи;
р = 0,95 – КПД клиноременной передачи;
ц = (0,96 – 0,98) – КПД цилиндрической передачи;
п = 0,99 – КПД одной пары подшипников.
КПД ременной передачи выбираем в соответствии с типом указанной ременной передачи в
пункте 5 исходных данных.
Значение КПД округляем до тысячных.
Р2
(1.2)
Р2 – мощность на выходном валу редуктора (смотри пункт 2 исходных данных)
Потребная мощность, кВт,
Рп
Значение потребной мощности округляем до сотых.
5

6.

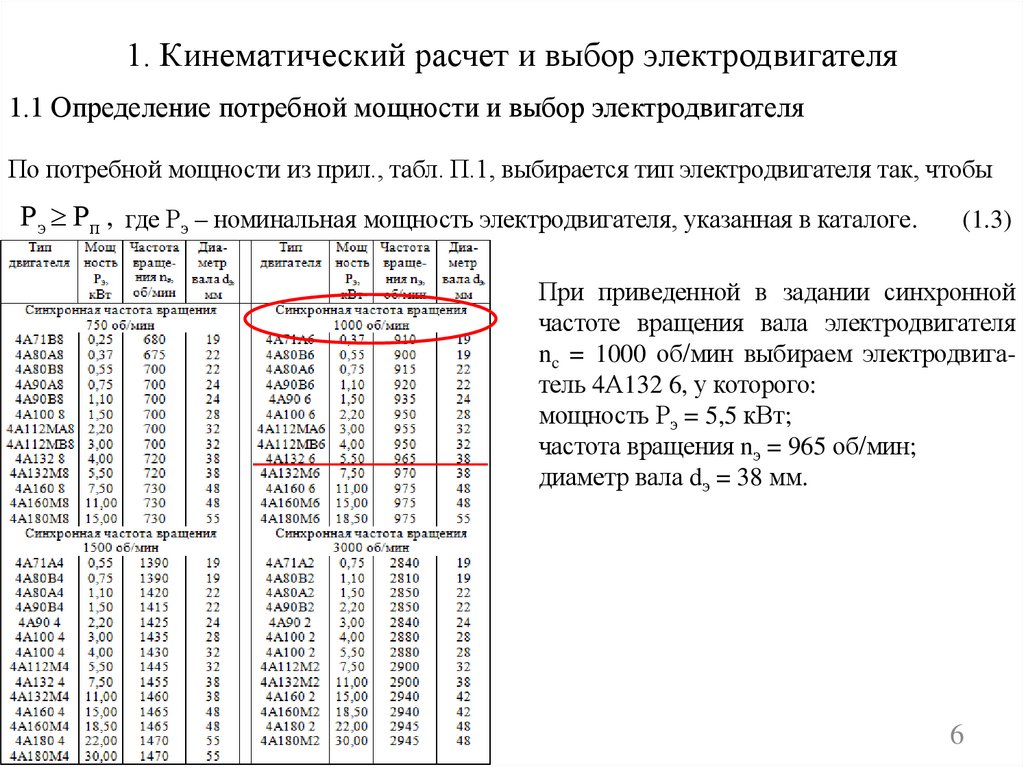
1. Кинематический расчет и выбор электродвигателя
1.1 Определение потребной мощности и выбор электродвигателя
По потребной мощности из прил., табл. П.1, выбирается тип электродвигателя так, чтобы
Рэ Рп , где Рэ – номинальная мощность электродвигателя, указанная в каталоге.
(1.3)
При приведенной в задании синхронной
частоте вращения вала электродвигателя
nc = 1000 об/мин выбираем электродвигатель 4А132 6, у которого:
мощность Рэ = 5,5 кВт;
частота вращения nэ = 965 об/мин;
диаметр вала dэ = 38 мм.
6

7.

1. Кинематический расчет и выбор электродвигателя
1.2 Определение передаточного числа и распределение его между типами и
ступенями передач
nэ
(1.4)
n2
где nэ – рабочая частота вращения вала электродвигателя, об/мин;
n2 – частота вращения выходного вала редуктора, об/мин (пункт 3 исходных данных).
Общее передаточное число привода
Uп
Значение общего передаточного числа округляем до сотых.
Общее передаточное число привода можно представить как произведение:
U п U рU
(1.5)
где Uр – передаточное число ременной передачи редуктора,
U – передаточное число редуктора.
Из условия рационального соотношения размеров диаметра ведомого шкива ременной
передачи и редуктора рекомендуется в расчетах принимать
1 Uр 2. (1.6)
Принимаем передаточное число ременной передачи Uр = 1,5
Передаточное число редуктора
U
Uп
Uр
(1.7)
Значение передаточного числа округляем до сотых.
7

8.

1. Кинематический расчет и выбор электродвигателя
1.3 Частоты и угловые скорости вращения валов редуктора
Частоты, об/мин:
входной вал n1
nэ
Uр
выходной вал n 2
(1.8)
Значение округляем до сотых.
n1
(1.9)
U
Значение округляем до сотых.
Угловые скорости, с-1:
n1
входной вал 1
30
выходной вал 2
n 2
30
(1.10)
(1.11)
Значение округляем
до сотых.
Значение округляем
до сотых.
8

9.

1. Кинематический расчет и выбор электродвигателя
1.4 Мощности и вращающие моменты на валах редуктора
Мощности, кВт:
входной вал Р1 Р п р (1.12)
выходной вал Р2 Р1 ц п (1.13)
Значение округляем до сотых.
Значение округляем
до сотых.
Моменты, Н м:
Р
входной вал Т1 1 103 (1.14)
1
выходной вал Т 2
Р2
10 3 (1.15)
2
Значение округляем
до сотых.
Значение округляем
до сотых.
9

10.

2. Расчет и конструирование редуктора
2.1 Материалы зубчатых колес
Исходя из условий нарезания и прирабатываемости зубчатых колес назначаем
твердость шестерни от 300 НВ до 350 НВ.
НВ1 = 300 НВ.
Для лучшей приработки зубьев твердость шестерни рекомендуется назначать больше
твердости колеса на 30 50 единиц: НВ1 НВ2 + (30 – 50) НВ
НВ2 = 300-50 = 250 НВ
В соответствии с полученными твердостями шестерни и колеса, подбираем по
таблице необходимый материал для изготовления.
Механические свойства стали, применяемой для
изготовления зубчатых колес
Марка
стали
Диаметр заготовки,
мм
Твердость,
НВ, кгс/мм2
Термообработка
45
40Х
До 80
До 125
180 – 250
До 200
200 – 300
До 200
200 – 315
До 100
100 – 300
269 – 302
269 – 302
215 – 243
269 – 302
220 – 250
269 – 302
235 – 262
269 – 320
195 – 240
Улучшение
Улучшение
Улучшение
Улучшение
Нормализация
Улучшение
Улучшение
Улучшение
Нормализация
40ХН
35ХМ
50Г2
Шестерня:
сталь 40ХН;
твердость 300 НВ;
термообработка –
улучшение.
Колесо:
сталь 35ХМ;
твердость 250 НВ;
термообработка –
улучшение.
10

11.

2. Расчет и конструирование редуктора
2.2 Определение геометрических и кинематических параметров редуктора
Так как редуктор выполняется в виде самостоятельного механизма, то соответствии с
ГОСТ 21354-87 основным параметром передачи является межосевое расстояние a
а К а ( U 1)3
Т 2 К н
2
U 2 bа нр
(2.1)
где Ка = 430 – вспомогательный коэффициент для косозубых передач;
U – передаточное число редуктора (формула 1.7);
Т2 – вращающий момент на выходном валу, Н м (формула 1.15);
Кн – коэффициент, учитывающий неравномерность распределения нагрузки по
ширине венца, принимается по графику в зависимости от параметра bd,
bd 0,5 ba ( U 1), (2.2)
где bа – коэффициент ширины зубчатого
колеса относительно межосевого расстояния,
принимается из ряда: 0,4; 0,5; 0,63; 0,8.
Принимаем bа = 0,5, тогда:
И из графика Кн = 1,12
11

12.

2. Расчет и конструирование редуктора
2.2 Определение геометрических и кинематических параметров редуктора
Определим суммарное число циклов напряжений, миллионов циклов: Nk = 60 n Lh
где n – частота вращения шестерни или колеса, об/мин (формула 1.8 или 1.9);
Lh – требуемый ресурс передачи, ч (смотри пункт 9 исходных данных).
Для шестерни
Для колеса
Базовое число циклов напряжений,
миллионов циклов,
N H lim 30HB2, 4 120 106
Для шестерни
Коэффициент долговечности Z N 6
Z N 20
Для шестерни
Так как Nk NH lim, то
(2.3)
соответствующее пределу
(2.4)
Для колеса
выносливости,
N H lim
Nk
при Nk NH lim , но не более 2,6;
N H lim
Nk
при Nk NH lim , но не менее 0,75
(2.5)
Для колеса
Так как Nk NH lim, то
12

13.

2. Расчет и конструирование редуктора
2.2 Определение геометрических и кинематических параметров редуктора
Предел контактной усталости поверхностей зубьев, соответствующий базовому числу
(2.6)
циклов напряжений, МПа:
н lim b = 2НВ + 70
Для шестерни
Для колеса
Допускаемое контактное напряжение для материала:
(2.7)
SН = 1,1 – коэффициент запаса прочности для зубчатых колес с однородной структурой
материала
При выполнении расчетов принять ZRZVZLZX = 0,9,
где ZR – коэффициент, учитывающий влияние исходной шероховатости сопряженных
поверхностей зубьев;
ZV – коэффициент, учитывающий влияние окружной скорости;
ZL – коэффициент, учитывающий влияние смазочного материала;
ZХ – коэффициент, учитывающий размер зубчатого колеса.
Для шестерни
Для колеса
13

14.

2. Расчет и конструирование редуктора
2.2 Определение геометрических и кинематических параметров редуктора
Допускаемое контактное напряжение для косозубой передачи, МПа:
нр 0,45( нр1 нр 2 ),
(2.8)
Возвращаемся к формуле (2.1) и определяем межосевое расстояние, мм:
Определяем модуль зубчатой передачи и выбираем стандартное значение из диапазона, мм:
m (0,01 0,02)а
(2.9)
Стандартные значения модуля зубьев
Ряд
1-й
2-й
1,0
1,25
1,25
1,375
1,5
1,75
2,0
2,25
2,5
2,75
Модуль, мм
3,0
4,0
3,5
4,5
5,0
5,5
6,0
7,0
8,0
9,0
10,0
11,0
12,0
14,0
Принимаем по первому ряду m = 2 мм.
14

15.

2. Расчет и конструирование редуктора
2.2 Определение геометрических и кинематических параметров редуктора
Сумма зубьев шестерни и колеса ZC
2a cos
m
(2.10)
где = (8 – 18°) – угол наклона линии зуба (выбираем из интервала).
Принимаем угол = 15°, тогда:
Суммарное число зубьев обязательно округляем до
ближайшего целого числа.
Число зубьев шестерни
Z
(2.11)
Z1 C .
U 1
Число зубьев колеса Z2 = ZC – Z1. (2.12)
Число зубьев шестерни обязательно
округляем до ближайшего целого числа.
Z2 = 118 – 28 = 90
Уточненное значение угла наклона зубьев arccos
( Z1 Z 2 )m (2.13)
.
2a
15

16.

2. Расчет и конструирование редуктора
2.2 Определение геометрических и кинематических параметров редуктора
Делительные диаметры, мм:
d1
mZ1
;
cos
d2
(2.14)
mZ 2
cos
(2.15)
Диаметры вершин зубьев, мм:
d a 2 d 2 2m. (2.17)
d a1 d1 2m; (2.16)
Диаметры впадин зубьев, мм:
d f 2 d 2 2,5m (2.19)
d f 1 d1 2,5m; (2.18)
Уточненное межосевое расстояние, мм,
а 0,5(d1 d 2 ). (2.20)
Рабочая ширина зубчатого венца b , равная ширине венца колеса b2, мм,
Округляем до целого
b b 2 ba a (2.21)
Ширина венца шестерни, мм,
b1 b 2 m. (2.22)
Округляем до целого
Окружная скорость зубчатых колес, м/с,
d1n1
v1
(2.23)
60 1000
Выбираем 8-ю степень точности
16

17.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
Проверочный расчет зубьев заключается в сравнении рабочих контактных напряжений с
допускаемыми. Заключение о способности зубчатой передачи выдерживать рабочие
нагрузки можно сделать в том случае, если рабочие контактные напряжения будут меньше,
чем допускаемые.
H НР
Рабочее контактное напряжение, МПа
Ft1 U 1
K A K HV K H K H
(2.24)
b1d1 U
где ZE = 190 – коэффициент, учитывающий механические свойства материалов
сопряженных зубчатых колес, изготовленных из стали;
ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе
зацепления,
H Z E Z H Z
ZH
1
cos t
2 cos b
tg t
(2.25)
где t – делительный угол профиля в торцовом сечении, град,
t arctg
tg 20
(2.26)
cos
где угол наклона линии зуба, град;
t угол зацепления, град, для передач без смещения t t
17

18.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
b – основной угол наклона, град,
b arcsin(sin cos 20 ); (2.27)
Z коэффициент, учитывающий суммарную длину контактных линий,
1
(2.28)
где коэффициент торцового перекрытия,
Z
1
1
cos (2.29)
1,88 3,22
Z
Z
1
2
Ft1 – окружная сила на делительном диаметре шестерни, Н,
2T1
Ft1
d1
(2.30)
где Т1 – момент, Н мм
18

19.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
KА = 1,1 – коэффициент внешней динамической нагрузки при равномерном нагружении
двигателя и ведомой машины
КHV – коэффициент, учитывающий динамическую нагрузку
HV b1
(2.31)
Ft1K A
где HV – удельная окружная динамическая сила, Н/мм
К HV 1
a
, (2.32)
U
где Н = 0,02 – коэффициент, учитывающий влияние вида зубчатой передачи
HV Н q o v1
qо – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и
колеса 8-й степени точности
qo = 5,6
при m 3,55 мм;
qo = 6,1
при 10 m 3,55 мм
19

20.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
КН коэффициент, учитывающий неравномерность распределения нагрузки по длине
контактных линий
К Н 1 (К оН 1)К Н , (2.33)
о
где К Н коэффициент, учитывающий неравномерность распределения нагрузки по
длине контактных линий в начальный период работы передачи
К
о
Н
0,04b1f kyo C cos t
1
, (2.34)
2
Ft1K A K HV Z
f kyo фактическое отклонение положения контактных линий в начальный период работы
передачи
f kyo a F , (2.35)
где а = 0,3 – коэффициент, учитывающий статистическое распределение погрешностей и
критерии допустимого повреждения активных поверхностей зубьев
F – допуск на погрешность направления зубьев
Степень точности
Модуль, мм
8
От 1 до 40
Ширина венца зубчатого колеса, мм
до 40
св. 40 до 100
св. 100 до 160
св. 160 до 250
18
25
32
40
20

21.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
С – удельная нормальная жесткость пары зубьев, Н/мм мкм
1
0,1425 0,1860
0,05139
, (2.36)
С
Z V1
ZV 2
где ZV1, ZV2 – эквивалентные числа зубьев шестерни и колеса соответственно
ZV1
Z1
; (2.37)
cos3
ZV 2
Z2
; (2.38)
3
cos
КН – коэффициент, учитывающий приработку зубьев
20
, (2.39)
(0,01НВ 2 2) 2 ( v1 4) 0, 25
где НВ2 – твердость материала зубчатого колеса, МПа;
v1 – окружная скорость, м/с
К Н 1
21

22.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
КН – коэффициент, учитывающий распределение нагрузки между зубьями
К Н 0,9 0,4
2( 1)С b1 (a f pbe Y )
Ft1K A K Hv K H
, (2.40)
суммарный коэффициент перекрытия
, (2.41)
коэффициент торцового перекрытия
1 2 ; (2.42)
1
Z1 ( tg 1 tg t )
2
(2.43)
2
Z 2 ( tg 2 tg t )
, (2.44)
2
1 , 2 углы профиля зуба в точках на окружностях вершин, град
d
1 arccos b1 (2.45)
d a1
d
2 arccos b 2 (2.46)
da2
d b1 , d b 2 основные диаметры шестерни и колеса, мм
d b1 d1 cos t ; (2.47)
d b 2 d 2 cos t ; (2.48)
22

23.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
коэффициент осевого перекрытия
b
1 , (2.49)
Px
где Рх – осевой шаг, мм
Px
m
; (2.50)
sin
Степень
точности
8
Модуль
m, мм
Диаметр делительной окружности,
мм
св. 50
св. 125
св. 280
до 50
до 125
до 280
до 560
От 1 до 2
20
21
22
24
Св. 2 до 3,55
21
22
24
26
По формуле (2.41):
С средняя удельная торцовая жесткость зубьев пары зубчатых колес, Н/(мм мкм)
С С (0,75 0,25); (2.51)
а 0,2 коэффициент, учитывающий статистическое распределение погрешностей и
критерии допустимого повреждения поверхностей зубьев
f pbe предельное отклонение шага зацепления, мкм
f pbе f pb2 1 f pb2 2 , (2.52)
f pb1,f pb 2 предельное отклонение шага зацепления шестерни и колеса соответственно, мкм
23

24.

2. Расчет и конструирование редуктора
2.2.1 Проверочный расчет зубьев колес на контактную прочность
Y – уменьшение погрешности шага зацепления в результате приработки, мкм
Y
Y 1
Y 2
Y 1 Y 2
;
2
160
H lim b1
160
H lim b 2
f pb1
(2.53)
(2.54)
f pb2 . (2.55)
По формуле (2.40):
По формуле (2.24):
Проверяем условие прочности по контактным напряжениям:
Условие прочности по контактным напряжениям выполняется, следовательно,
геометрические параметры передачи подходят под возникающие нагрузки.
24

25.

2. Расчет и конструирование редуктора
2.2.2 Расчет зубьев на прочность при изгибе
Выносливость зубьев, необходимую для предотвращения усталостного излома,
устанавливают для каждого колеса сопоставлением расчетного местного напряжения от
изгиба в опасном сечении на переходной поверхности и допускаемого напряжения
F FP .
Расчетное местное напряжение при изгибе
Ft
K F YFS Y Y , (2.56)
bmm
где KF – коэффициент нагрузки
K F K A K FV K F K F , (2.57)
F
где KFV – коэффициент, учитывающий динамическую нагрузку, возникающую в
зацеплении до зоны резонанса
b
K FV 1 FV 1 , (2.58)
Ft1K A
FV удельная окружная динамическая сила, Н/мм
FV Fq o v1
a
, (2.59)
U
F 0,06 коэффициент, учитывающий влияние вида зубчатой передачи и
модификации профиля зубьев
25

26.

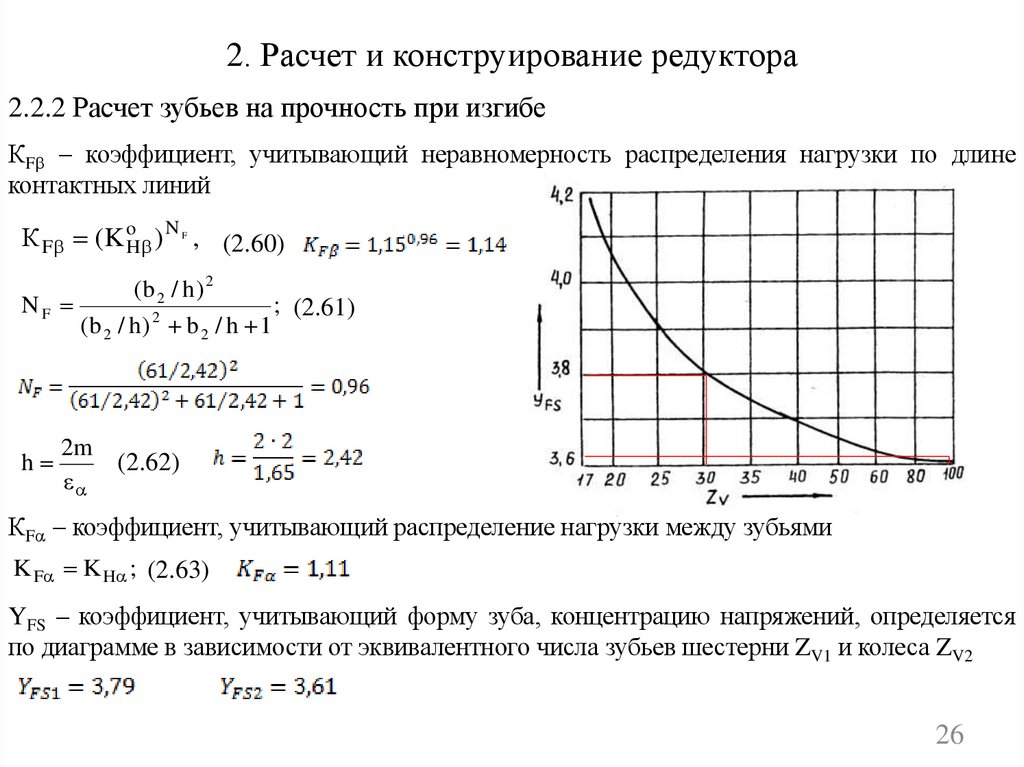
2. Расчет и конструирование редуктора
2.2.2 Расчет зубьев на прочность при изгибе
КF коэффициент, учитывающий неравномерность распределения нагрузки по длине
контактных линий
К F (K oH ) N , (2.60)
F
(b 2 / h ) 2
NF
; (2.61)
(b 2 / h ) 2 b 2 / h 1
h
2m
(2.62)
КF коэффициент, учитывающий распределение нагрузки между зубьями
K F K H ; (2.63)
YFS – коэффициент, учитывающий форму зуба, концентрацию напряжений, определяется
по диаграмме в зависимости от эквивалентного числа зубьев шестерни ZV1 и колеса ZV2
26

27.

2. Расчет и конструирование редуктора
2.2.2 Расчет зубьев на прочность при изгибе
Y коэффициент, учитывающий наклон зуба
Y 1
0,7; (2.64)
120
Так как расчетное значение коэффициента получилось меньше 0,7, то принимаем Y = 0,7
По формуле (2.57):
Y коэффициент, учитывающий перекрытие зубьев
Y 0,2
0,8
(2.65) при 1
Y
1
(2.66) при 1.
Напряжения при изгибе
для шестерни
F1
Ft1
K F YFS1 Y Y (2.67)
b1 m
для колеса
Y
F2 F1 FS2 . (2.68)
YFS1
27

28.

2. Расчет и конструирование редуктора
2.2.2 Расчет зубьев на прочность при изгибе
Допускаемое напряжение
FP
F limb
YN Y YR YX , (2.69)
SF
F lim b предел выносливости зубьев при изгибе, МПа
Flim b oFlim b YT YZ Yq Yd YA , (2.70)
oF lim b предел выносливости зубьев при изгибе, соответствующий базовому числу
циклов напряжений, МПа
oF lim b 1,75НВ (2.71)
YT = 1 – коэффициент, учитывающий технологию изготовления зубчатых колес;
YZ = 1 – коэффициент, учитывающий способ получения заготовки зубчатого колеса
(ковка или штамповка);
Yq = 1 – коэффициент, учитывающий отсутствие шлифования переходной поверхности
зубьев;
Yd = 1 – коэффициент, учитывающий отсутствие деформационного упрочнения или
электрохимической обработки переходной поверхности;
YA = 1 – коэффициент, учитывающий влияние характера приложения нагрузки
(одностороннее);
28

29.

2. Расчет и конструирование редуктора
2.2.2 Расчет зубьев на прочность при изгибе
YN = 1 – коэффициент долговечности
Y коэффициент, учитывающий чувствительность материала к концентрации напряжений
Y 1,082 0,172 lg m; (2.72)
YR = 1,2 – коэффициент, учитывающий шероховатость переходной поверхности (при
нормализации и улучшении);
Yх коэффициент, учитывающий размеры зубчатого колеса
Yx 1,05 0,000125 d, (2.73)
где d – диаметр делительной окружности зубчатого колеса, мм
SF = 1,7 – коэффициент запаса прочности для углеродистой и легированной стали,
подвергнутых нормализации или улучшению
Допускаемые напряжения, МПа
FP1
F limb1
YN Y YR YX1
SF
(2.74)
FP 2
F limb 2
YN Y YR YX 2 (2.75)
SF
Условие прочности при изгибе выполняется для обоих колес
29

30.

30
2. Расчет и конструирование редуктора
2.3 Ориентировочный расчет и конструирование валов
Входной вал
Диаметр концевого участка вала
T1
d1 3
, (2.76)
0,2 k
где Т1 – вращающий момент на валу,
Н мм;
[ k] = (20 – 25) МПа – допускаемое
напряжение кручения
20
45
d, мм
22
50
25
55
28
60
32
70
36
80
40
90
42 – 50
2,8
3,0
1,6
52 – 60
3,0
3,0
2,0
62 – 70
3,3
3,5
2,0
72 – 85
3,5
3,5
2,5
25
42
60
80
26
44
62
85
28
45
63
90
Округляем до стандартного
Диаметр вала под уплотнение
d упл d1 2t , (2.77)
где t – высота буртика
Округляем до стандартного
d
t
r
f
17 – 24
2,0
1,6
1,0
25 – 30
2,2
2,0
1,0
32 – 40
2,5
2,5
1,2
dупл
20
35
52
68
21
36
55
70
22
38
56
71
24
40
58
75
30
48
65
95
32
50
67
100

31.

31
2. Расчет и конструирование редуктора
2.3 Ориентировочный расчет и конструирование валов
Диаметр вала dп в месте посадки
подшипника может быть равен
диаметру вала под уплотнением или
больше его, но кратен пяти.
Принимаем dп = 35 мм
Диаметр кольца со стороны подшипника
d б.п d п 3r, (2.78)
где r – координата фаски
подшипника
Округляем до стандартного
Диаметр вала под шестерней
dб.п dк dп (2.79)
Диаметр
разделительного
кольца со стороны шестерни
d б.к d k 3f , (2.80)
где f размер фаски
d
t
r
f
17 – 24
2,0
1,6
1,0
20
36
63
85
112
21
38
65
88
115
25 – 30
2,2
2,0
1,0
22
40
67
90
118
32 – 40
2,5
2,5
1,2
24
42
70
92
120
25
45
71
95
125
42 – 50
2,8
3,0
1,6
52 – 60
3,0
3,0
2,0
26
48
73
100
130
28
50
75
102
135
Округляем до стандартного
62 – 70
3,3
3,5
2,0
30
53
78
105
140
32
55
80
108
145
72 – 85
3,5
3,5
2,5
34
60
82
110
150

32.

32
2. Расчет и конструирование редуктора
2.3 Ориентировочный расчет и конструирование валов
Выходной вал
Диаметр концевого участка вала
Т2
d2 3
, (2.81)
0,2 k
где Т2 – вращающий момент на валу,
Н мм;
[ k] = (20 – 25) МПа – допускаемое
напряжение кручения
Округляем до стандартного
Диаметр вала под уплотнение
d упл d 2 2t, (2.82)
где t – высота буртика
Округляем до стандартного
20
45
d, мм
22
50
25
55
28
60
32
70
36
80
40
90
42 – 50
2,8
3,0
1,6
52 – 60
3,0
3,0
2,0
62 – 70
3,3
3,5
2,0
72 – 85
3,5
3,5
2,5
25
42
60
80
26
44
62
85
28
45
63
90
d
t
r
f
17 – 24
2,0
1,6
1,0
25 – 30
2,2
2,0
1,0
32 – 40
2,5
2,5
1,2
dупл
20
35
52
68
21
36
55
70
22
38
56
71
24
40
58
75
30
48
65
95
32
50
67
100

33.

33
2. Расчет и конструирование редуктора
2.3 Ориентировочный расчет и конструирование валов
Диаметр вала dп в месте посадки
подшипника может быть равен
диаметру вала под уплотнением или
больше его, но кратен пяти.
Принимаем dп = 45 мм
Диаметр кольца со стороны подшипника
d б.п d п 3r, (2.83)
где r – координата фаски
подшипника
Округляем до стандартного
Диаметр вала под шестерней
dб.п dк dп (2.84)
Диаметр
разделительного
кольца со стороны шестерни
d б.к d k 3f , (2.85)
где f размер фаски
d
t
r
f
17 – 24
2,0
1,6
1,0
20
36
63
85
112
21
38
65
88
115
25 – 30
2,2
2,0
1,0
22
40
67
90
118
32 – 40
2,5
2,5
1,2
24
42
70
92
120
25
45
71
95
125
42 – 50
2,8
3,0
1,6
52 – 60
3,0
3,0
2,0
26
48
73
100
130
28
50
75
102
135
Округляем до стандартного
62 – 70
3,3
3,5
2,0
30
53
78
105
140
32
55
80
108
145
72 – 85
3,5
3,5
2,5
34
60
82
110
150

34.

2. Расчет и конструирование редуктора
2.4 Выбор подшипников качения
Исходя из действующих нагрузок в косозубой
передаче (радиальные и осевые), выбираем
тип подшипника – шариковый радиальноупорный.
Подбираем подшипник
по посадочному
диаметру dп для входного
и выходного валов.
Для входного вала при посадочном диаметре dп = 35 мм выбираем подшипник 36207.
Для него d = 35 мм, D = 72 мм, B = 17 мм, r = 2 мм, r1 = 1 мм, Cr = 30,8 кН, Cor = 17,8 кН.
Для выходного вала при посадочном диаметре dп = 45 мм выбираем подшипник 36209.
Для него d = 45 мм, D = 85 мм, B = 19 мм, r = 2 мм, r1 = 1 мм, Cr = 41,2 кН, Cor = 25,1 кН.
34

35.

35
2. Расчет и конструирование редуктора
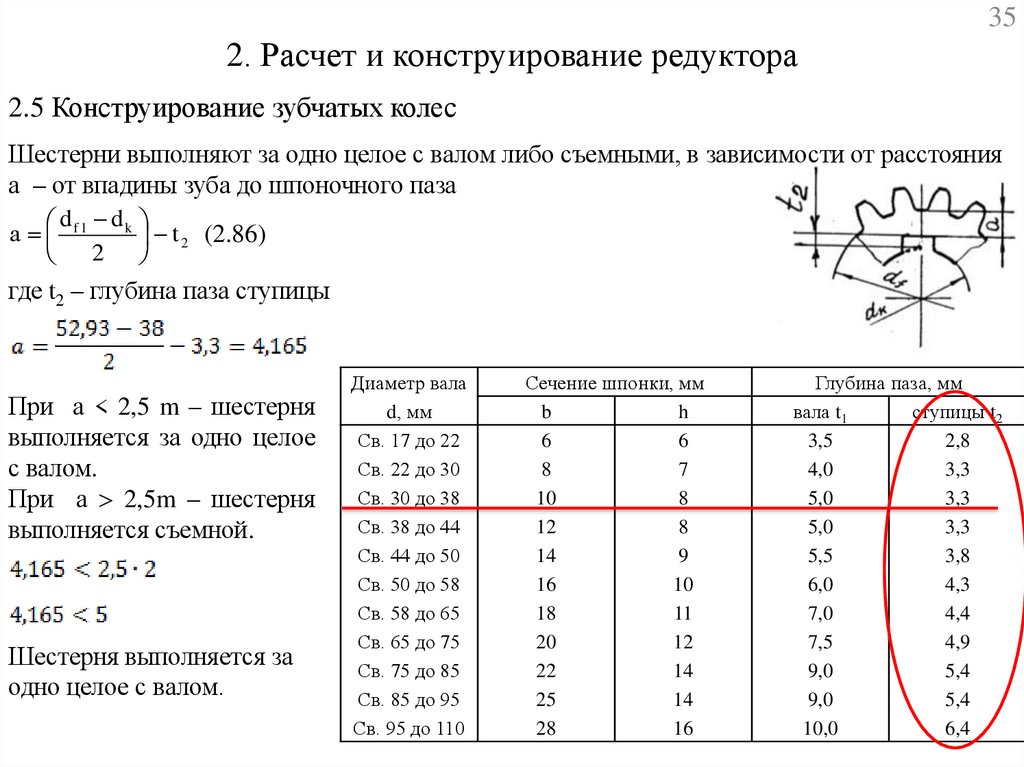
2.5 Конструирование зубчатых колес
Шестерни выполняют за одно целое с валом либо съемными, в зависимости от расстояния
а – от впадины зуба до шпоночного паза
d dk
а f1
t 2 (2.86)
2
где t2 – глубина паза ступицы
При а < 2,5 m – шестерня
выполняется за одно целое
с валом.
При а 2,5m – шестерня
выполняется съемной.
Шестерня выполняется за
одно целое с валом.
Диаметр вала
d, мм
Св. 17 до 22
Св. 22 до 30
Св. 30 до 38
Св. 38 до 44
Св. 44 до 50
Св. 50 до 58
Св. 58 до 65
Св. 65 до 75
Св. 75 до 85
Св. 85 до 95
Св. 95 до 110
Сечение шпонки, мм
b
h
6
6
8
7
10
8
12
8
14
9
16
10
18
11
20
12
22
14
25
14
28
16
Глубина паза, мм
вала t1
ступицы t2
3,5
2,8
4,0
3,3
5,0
3,3
5,0
3,3
5,5
3,8
6,0
4,3
7,0
4,4
7,5
4,9
9,0
5,4
9,0
5,4
10,0
6,4

36.

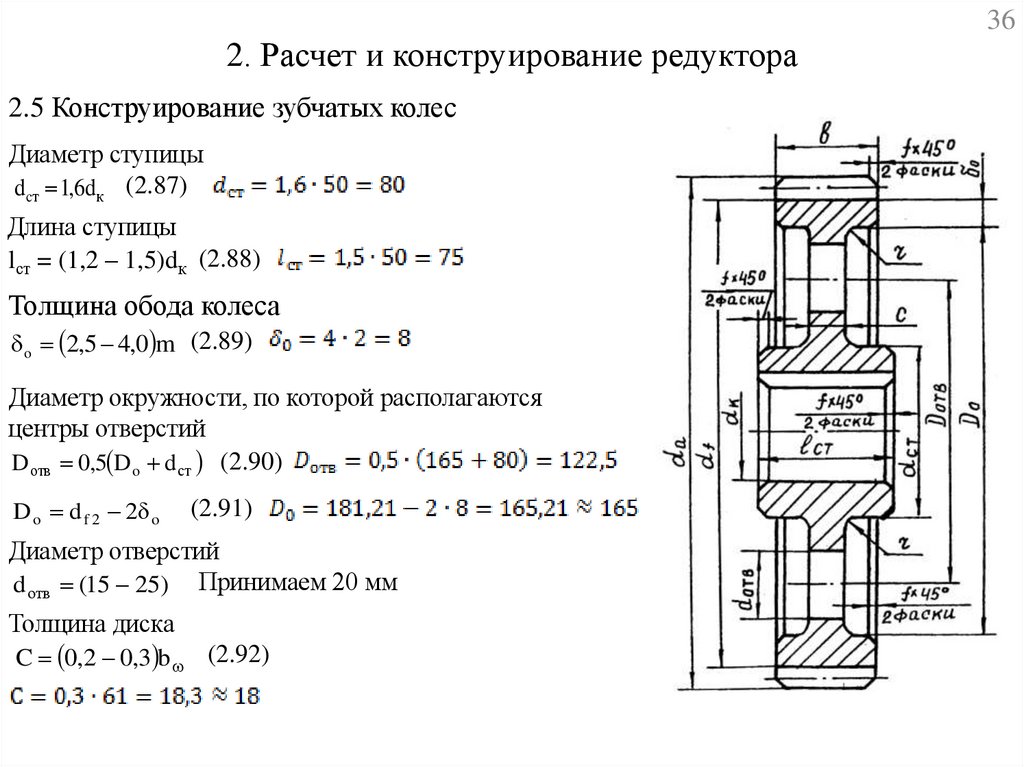
2. Расчет и конструирование редуктора
2.5 Конструирование зубчатых колес
Диаметр ступицы
d cт 1,6d к (2.87)
Длина ступицы
lст = (1,2 – 1,5)dк (2.88)
Толщина обода колеса
o 2,5 4,0 m (2.89)
Диаметр окружности, по которой располагаются
центры отверстий
D отв 0,5 D o d ст (2.90)
D o d f 2 2 o
(2.91)
Диаметр отверстий
d отв (15 25) Принимаем 20 мм
Толщина диска
C 0,2 0,3 b (2.92)
36

37.

2. Расчет и конструирование редуктора
37
2.6 Конструирование крышек подшипников
При конструировании крышек определяющим размером является диаметр D отверстия в
корпусе под подшипник.
D, мм 50 – 62 63 – 95 100 – 145 150 – 200
Для входного
Для выходного
, мм
5
6
7
8
D = 72
D = 85
d4, мм
6
8
10
12
=6
=6
z
4
4
6
6
d4 = 8
d4 = 8
z=4
z=4
1 1,2 (2.93)
2 0,9 1,0 (2.94)
Dф D 4,0 4,4 d 4 (2.95)
d отв d 4 1 (2.96)
C d 4 (2.97)
D в D 2С (2.98)
d в d упл 1 (2.99)

38.

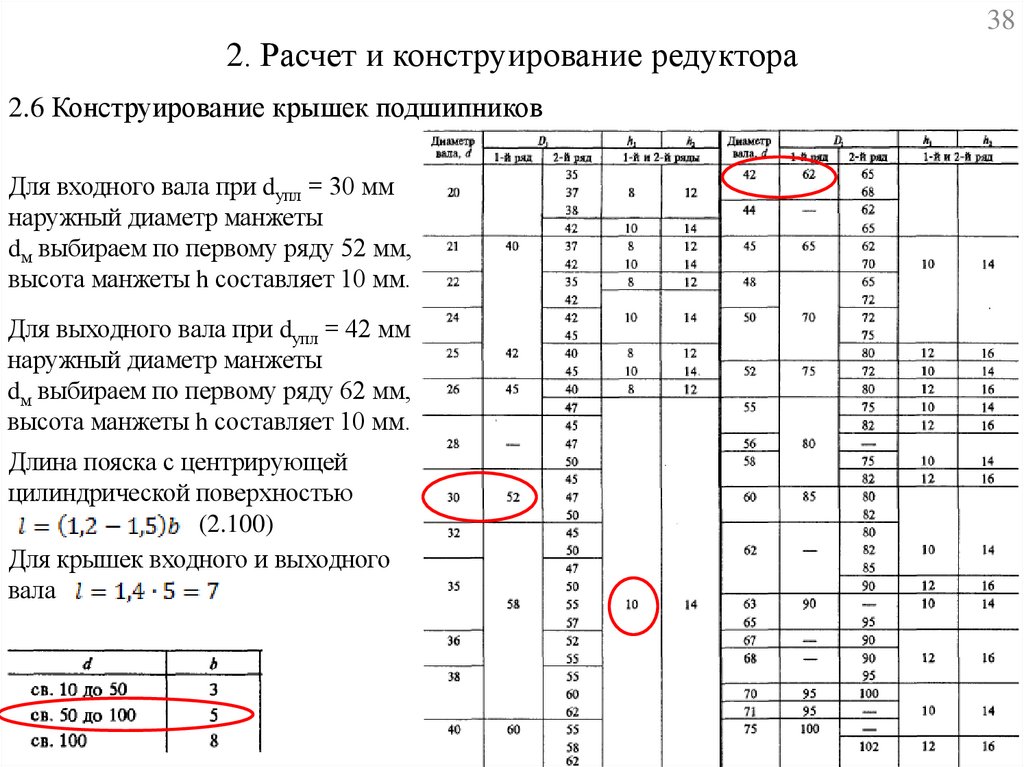
2. Расчет и конструирование редуктора
2.6 Конструирование крышек подшипников
Для входного вала при dупл = 30 мм
наружный диаметр манжеты
dм выбираем по первому ряду 52 мм,
высота манжеты h составляет 10 мм.
Для выходного вала при dупл = 42 мм
наружный диаметр манжеты
dм выбираем по первому ряду 62 мм,
высота манжеты h составляет 10 мм.
Длина пояска с центрирующей
цилиндрической поверхностью
(2.100)
Для крышек входного и выходного
вала
38

39.

2. Расчет и конструирование редуктора
2.6 Конструирование корпуса редуктора
Толщина стенки корпуса к и крышки 1к редуктора
к = 0,025 а + 3 (2.101)
1к = 0,02 а + 3 (2.102)
Так как в результате расчетов оказалось что к 8 и 1к 8, то принимаем к = 1к = 8 мм
Толщина верхнего фланца основания корпуса редуктора и фланца крышки редуктора
b = 1,5 к (2.103)
b1 = 1,5 1к (2.104)
Толщина нижнего фланца основания корпуса редуктора
р = 2,35 к (2.105)
Толщина ребер жесткости основания m и крышки m1 редуктора
m 0,85 1 к (2.106)
m1 0,85 1 1к (2.107)
39

40.

40
2. Расчет и конструирование редуктора
2.6 Конструирование корпуса редуктора
Диаметр фундаментных болтов
d1 0,03 0,036 а 12 (2.108)
Стандартный диаметр
Ki
М8
24
М10
28
Болт
М12
33
Ci
13
16
18
19,5
21
М20
48
Болт
М24
54
М27
58
М30
65
25
34
36
40
Параметр
Параметр
Диаметр болтов у подшипников
Ki
М18
44
d 2 0,7 0,75 d1 (2.109)
Ci
23
Стандартный диаметр
Диаметр болтов, соединяющих основание
корпуса с крышкой
d3 = (0,5 0,6) d1 (2.110)
Стандартный диаметр
Диаметр винтов, крепящих смотровую крышку
d5 = (0,3 0,4) d1 (2.111)
Стандартный диаметр
Расположение оси
отверстия для болта
диаметром d2
е 1 1,2 d 2 . (2.112)
Диаметр гнезда
Dк Dф 2 5
М14
36
М16
39

41.

Размеры для построения компоновочной схемы редуктора
41
а - межосевое расстояние формула (2.20)
b1, b2 – ширина косозубой шестерни и косозубого колеса формулы (2.22) и (2.21)
d1, d2– делительный диаметр косозубой шестерни и косозубого колеса формулы (2.14) и (2.15)
lст – длина ступицы косозубого колеса формула (2.88)
dст – диаметр ступицы косозубого колеса (формула 2.87)
a – расстояние от торца косозубого колеса либо шестерни принимаем от 7 до 10 мм
a1 – расстояние от делительного диаметра колеса либо шестерни принимаем равным a + m
dп1, dп2 – посадочный диаметр подшипника входного и выходного вала (пункт 2.4)
D1, D2 – наружный диаметр подшипника входного и выходного вала (пункт 2.4)
Bп1, Bп2 – ширина подшипника входного и выходного вала (пункт 2.4)
δк – толщина стенки корпуса редуктора формула (2.101 (округленное значение))
К2 – ширина фланца у подшипника (после формулы 2.109)
δ – толщина крышки подшипника (входной и выходной вал выбраны в пункте 2.6)
δ1 – толщина фланца крышки подшипника (входной и выходной вал формула (2.93))
δ2 – толщина ножки крышки подшипника (входной и выходной вал формула (2.94))
Dф – диаметр фланца крышки подшипника (входной и выходной вал формула (2.95))
dм – наружный диаметр манжеты (входной и выходной вал выбран в пункте 2.6)
h – высота манжеты (входной и выходной вал выбран в пункте 2.6)
К3 – ширина верхнего фланца редуктора (после формулы 2.110)
Dк1, Dк2 – диаметр бобышки крышки подшипника входного и выходного валов (пункт 2.6)
d1, d2 – диаметры концевых участков входного и выходного валов формулы (2.76) и (2.81)
dупл1, dупл2 – диаметры под уплотнение входного и выходного валов формулы (2.77) и (2.82)
dб.п1, dб.п2 – диаметр бурта подшипника входного и выходного валов формулы (2.78) и (2.83)
dб.к1, dб.к2 – диаметр бурта колеса входного и выходного валов формулы (2.80) и (2.85)
l3, l5 – расстояния от крышек подшипников до шкива и муфты, принимаем от 10 до 15 мм
l4, l6 – длины концевых участков валов, принимаем 1,5 диаметра d1 и d2 соответственно

42.

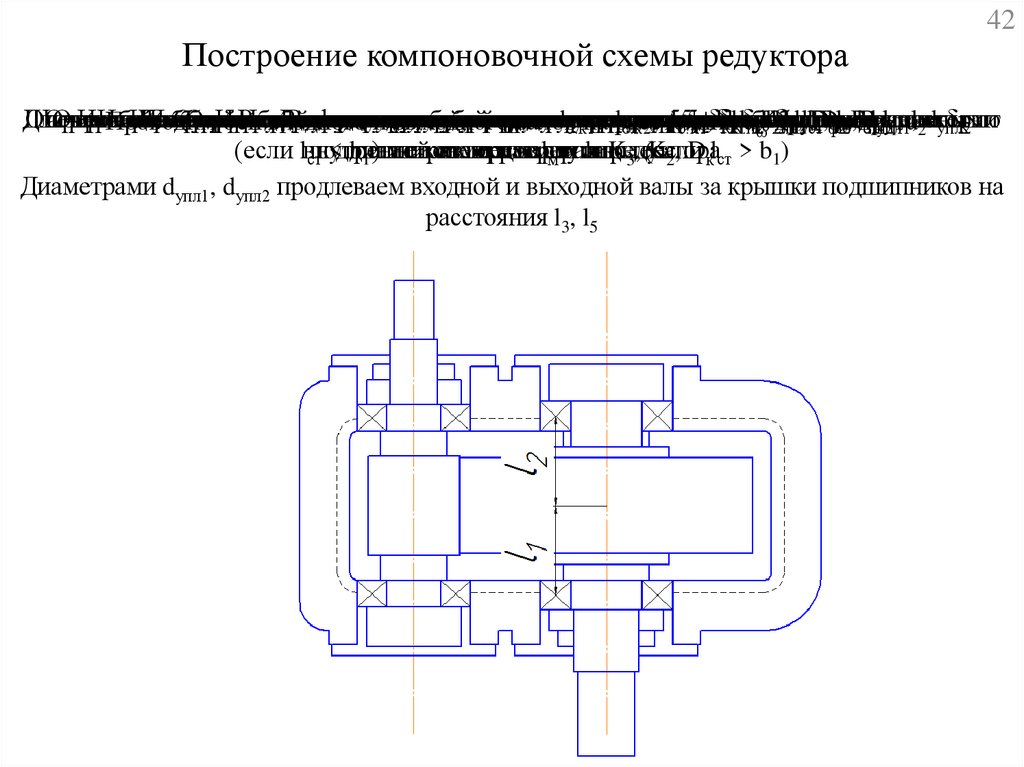
42
Построение компоновочной схемы редуктора
Очерчиваем
Изображаем
Изображаем
Очерчиваем
Очерчиваем
конструкцию
Изображаем
Радиусы
Изображаем
два
Радиус
ступицу
концевые
подшипника
крышки
скруглений
валов
косозубую
скруглений
косозубое
цилиндрического
по
подшипников
участки
размерам
входного
принять
шестерню
колесо
принять
валов
dравными
вала
по
колеса
по
равным
,по
размерам
dцентрами
размерам
по
размерам
, размерам
по
dразмерам
5б.п1
+размерам
,δbδ,
bδи
dK
d2друг
δd23от
и
d2п2
D
d,от
lделительных
,26,dB
,друга
dп1
Штриховой
Очерчиваем
Очерчиваем
Изображаем
линией
внутреннюю
внутреннюю
очерчиваем
два
Радиус
стенку
подшипника
стенку
скруглений
корпуса
корпуса
выходного
редуктора
принять
стенку
редуктора
корпуса
вала
равным
на
на
расстоянии
порасстоянии
редуктора
55для
+мм
δdКdподшипников
a,,dи
aна
торцов
D
B
δК по
от
Измеряем
расстояния
между
центром
колеса
и
l1шестерни
, l,2dупл2
Для
проходных
Изображаем
крышек
верхний
дополнительно
фланец
основания
очерчиваем
корпуса
ступень
редуктора
и
крышек
манжеты
Проводим
оси
входного
инаружную
выходного
на
расстоянии
а,бобышки
б.к1
б.к2
2размещения
б.п2
1+
11
п1
п1
ст
4расстоянии
ф
1и
п2
ст
упл1
К
1,1ll,от
п2
(если lвнутренней
< диаметров
b1) илиразмерам
от
торцов
шестерни
стенки
корпуса
редуктора
подшипников
по
размерам
dступицы
h колеса
K
K2, Dкlст > b1)
ст
м ии
3, (если
Диаметрами dупл1, dупл2 продлеваем входной и выходной валы за крышки подшипников на
расстояния l3, l5

43.

3. Расчет валов на совместное действие изгиба и кручения
Усилия, действующие в передачах:
окружные
радиальные
43
Валы редуктора нагружены силами,
действующими в зацеплении передачи, и
испытывают деформации изгиба и
кручения. Для упрощения расчетов принято,
что силы сосредоточенные, приложены в
серединах венцов зубчатых колес и
направлены по нормалям к профилям зубьев
в полюсах зацепления.
осевые
Ft1
2T1
d1
Fr1 Ft1
tg
cos
Fa1 Ft1tg
Ft 2
2T2
d2
Fr 2 Ft 2
tg
cos
Fa 2 Ft 2 tg

44.

3. Расчет валов на совместное действие изгиба и кручения
R A R 2AV R 2AH
2
2
R C R CV
R CH
44

45.

3. Расчет валов на совместное действие изгиба и кручения
Изгибающие моменты и эпюры, обусловленные действующими силами
участок вала АВ
М и R AV X
x 0,
участок вала ВC
M И RAV x Ft 2 ( x l1 ), Н м
x l1 ,
x l1 l2 ,
участок вала ВC
M И RAH x Fr 2 ( x l1 ) Fa 2
x l1 ,
x l1 l2 ,
x l1 ,
участок вала АВ
М и R AН X
x 0,
x l1 ,
d2
, Н м
2
45

46.

3. Расчет валов на совместное действие изгиба и кручения
46
Суммарные изгибающие моменты
2
М В М 2ВV М ВН
2
М В М 2ВV М ВН
Эквивалентный момент по третьей теории прочности
М экв М В2 Т 22
если М’В М”B
М экв М В 2 Т 22
если М’B < М”В
М экв
Диаметр вала в опасном сечении d 3
0,1 И
и = (50 60) МПа
Диаметр вала в опасном сечении не превышает предварительного, следовательно, подбор
геометрических параметров вала выполнен верно.

47.

4. Расчет подшипников качения
47
При частоте вращения кольца n 10 об/мин критерием расчета подшипника является
усталостное выкрашивание дорожек качения, расчет выполняют по динамической
грузоподъемности Сr. Суждение о пригодности подшипника выносится из сопоставления
значений требуемой и базовой грузоподъемности (Стр Сr) или долговечности (L10h L10h ).
Исходные данные для расчета подшипников:
Частота вращения вала n2 = 196,13об/мин
Базовая долговечность подшипника L10h = 24500 ч
Диаметр посадочных поверхностей вала dп = 45 мм
Действующие силы: радиальные
осевые
Статическая грузоподъемность Сor = 25100 Н
Динамическая грузоподъемность Сr = 41200 Н

48.

Fa
C or
0,014
0,018
0,023
0,029
0,034
0,040
0,046
0,052
0,057
0,066
0,076
0,086
0,094
0,104
0,110
0,140
0,170
0,230
0,290
0,330
0,380
0,430
0,570
Fa1
VFr
Х
0,45
Fa1
е
VFr
Y
1,81
1,76
1,69
1,62
1,60
1,56
1,52
1,49
1,46
1,44
1,41
1,34
1,30
1,25
1,22
1,18
1,13
1,08
1,04
1,03
1,02
1,01
1,00
Х
1
е
е
Y
0
0,300
0,311
0,324
0,340
0,345
0,352
0,358
0,365
0,370
0,382
0,396
0,410
0,425
0,440
0,450
0,465
0,480
0,500
0,520
0,526
0,533
0,540
0,540
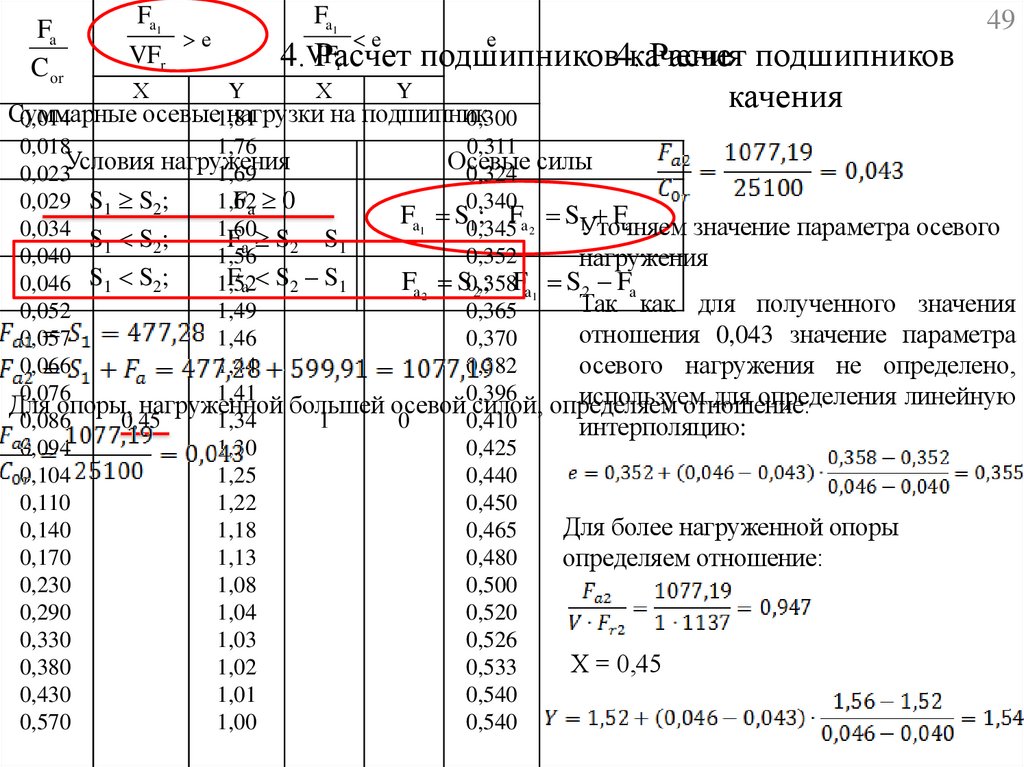
4. Расчет подшипников
качения
48
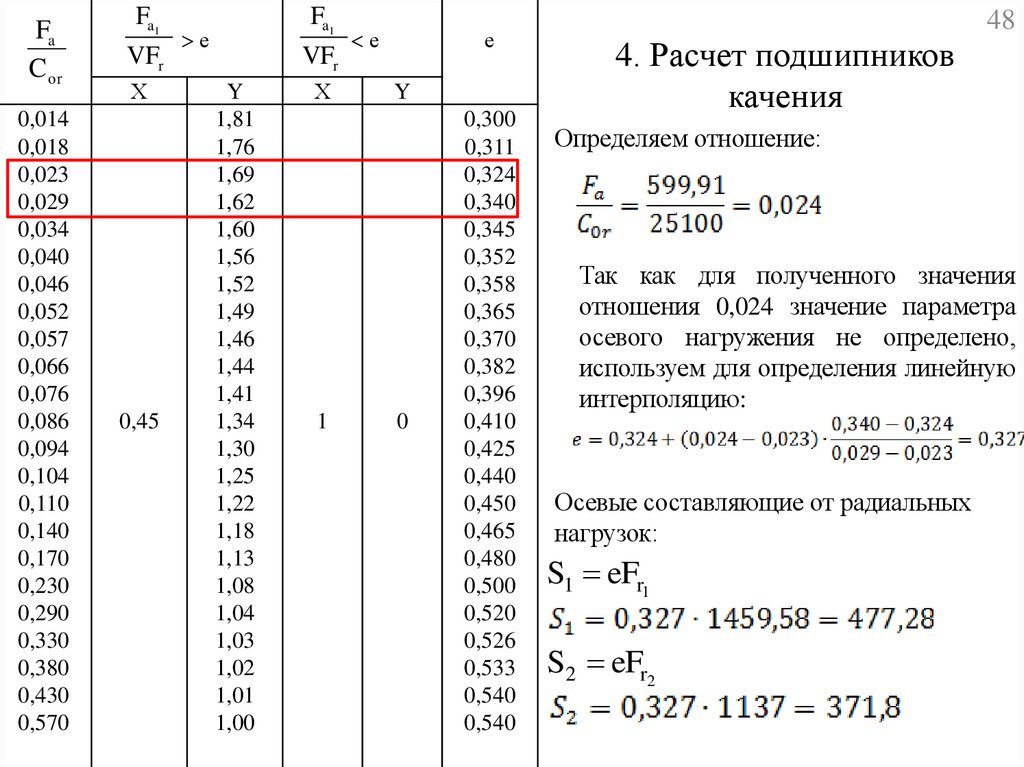
Определяем отношение:
Так как для полученного значения
отношения 0,024 значение параметра
осевого нагружения не определено,
используем для определения линейную
интерполяцию:
Осевые составляющие от радиальных
нагрузок:
S1 eFr1
S2 eFr2

49.

Fa
C or
Fa1
е
Fa1
е
е
4.VF
Расчет
подшипников4.качения
Расчет подшипников
r
Х
Y
Х
Y
качения
Суммарные осевые нагрузки на подшипник
VFr
49
0,014
1,81
0,300
0,018
1,76
0,311
Условия
нагружения
Осевые
0,023
1,69
0,324 силы
0,029 S1 S2;
1,62
0,340
Fa 0
F
S
Fa
a1
1 ; Fa 2 S1Уточняем
значение параметра осевого
0,034 S S ;
1,60
0,345
Fa S2 – S1
1
2
0,040
1,56
0,352
нагружения
Fa S2 – S1
Fa 2 S0,358
0,046 S1 S2;
1,52
2 ; Fa1 S2 Fa
Так как для полученного значения
0,052
1,49
0,365
отношения 0,043 значение параметра
0,057
1,46
0,370
0,066
1,44
0,382
осевого нагружения не определено,
0,076
1,41
0,396
используем
для определения линейную
Для опоры, нагруженной большей осевой силой, определяем
отношение:
0,086
0,45
1,34
1
0
0,410
интерполяцию:
0,094
1,30
0,425
0,104
1,25
0,440
0,110
1,22
0,450
Для более нагруженной опоры
0,140
1,18
0,465
0,170
1,13
0,480
определяем отношение:
0,230
1,08
0,500
0,290
1,04
0,520
0,330
1,03
0,526
Х = 0,45
0,380
1,02
0,533
0,430
1,01
0,540
0,570
1,00
0,540

50.

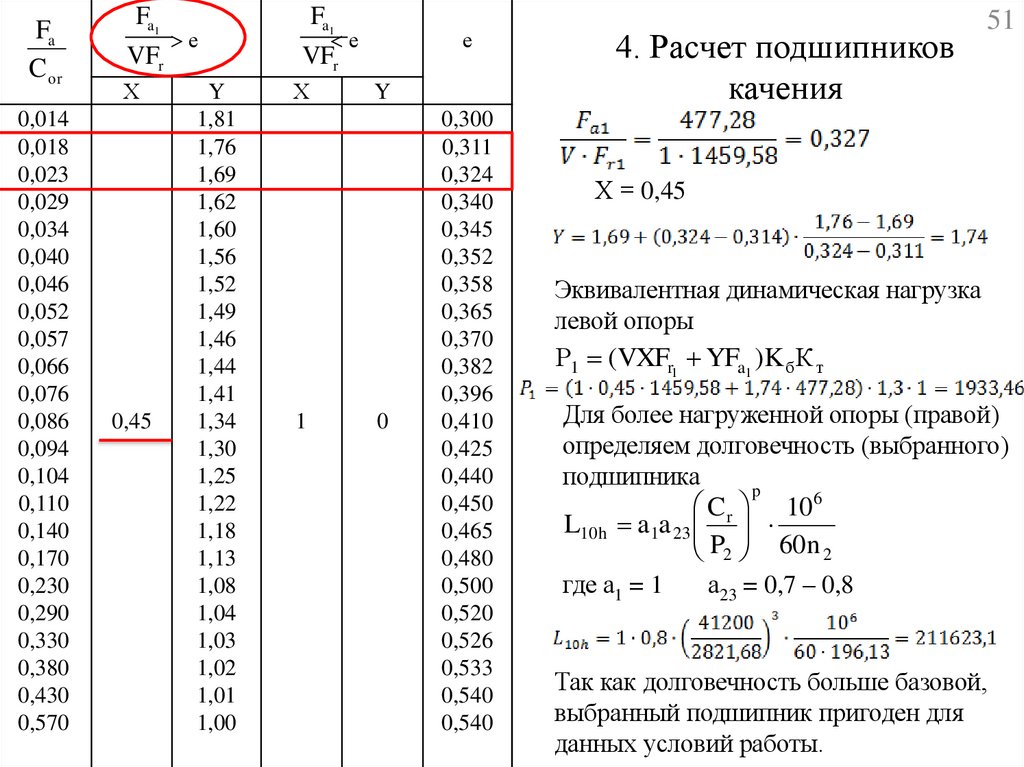
4. Расчет подшипников качения
Эквивалентная динамическая нагрузка правой опоры
Р 2 (VXFr2 YFa 2 )K б К т
где Кб = 1,3 – коэффициент безопасности;
Кт = 1 – температурный коэффициент
Уточняем коэффициент е для левой опоры
Для менее нагруженной опоры определяем отношение:
50
Fa
C or
е
0,014
0,018
0,023
0,029
0,034
0,040
0,046
0,052
0,057
0,066
0,076
0,086
0,094
0,104
0,110
0,140
0,170
0,230
0,290
0,330
0,380
0,430
0,570
0,300
0,311
0,324
0,340
0,345
0,352
0,358
0,365
0,370
0,382
0,396
0,410
0,425
0,440
0,450
0,465
0,480
0,500
0,520
0,526
0,533
0,540
0,540

51.

Fa
C or
0,014
0,018
0,023
0,029
0,034
0,040
0,046
0,052
0,057
0,066
0,076
0,086
0,094
0,104
0,110
0,140
0,170
0,230
0,290
0,330
0,380
0,430
0,570
Fa1
VFr
Х
0,45
е
Y
1,81
1,76
1,69
1,62
1,60
1,56
1,52
1,49
1,46
1,44
1,41
1,34
1,30
1,25
1,22
1,18
1,13
1,08
1,04
1,03
1,02
1,01
1,00
Fa1
е
е
VFr
Х
1
Y
0
0,300
0,311
0,324
0,340
0,345
0,352
0,358
0,365
0,370
0,382
0,396
0,410
0,425
0,440
0,450
0,465
0,480
0,500
0,520
0,526
0,533
0,540
0,540
4. Расчет подшипников
качения
51
Х = 0,45
Эквивалентная динамическая нагрузка
левой опоры
Р1 (VXFr1 YFa1 )K б К т
Для более нагруженной опоры (правой)
определяем долговечность (выбранного)
подшипника
p
C r 10 6
L10 h a1a 23
P2 60 n 2
где а1 = 1
а23 = 0,7 – 0,8
Так как долговечность больше базовой,
выбранный подшипник пригоден для
данных условий работы.

52.

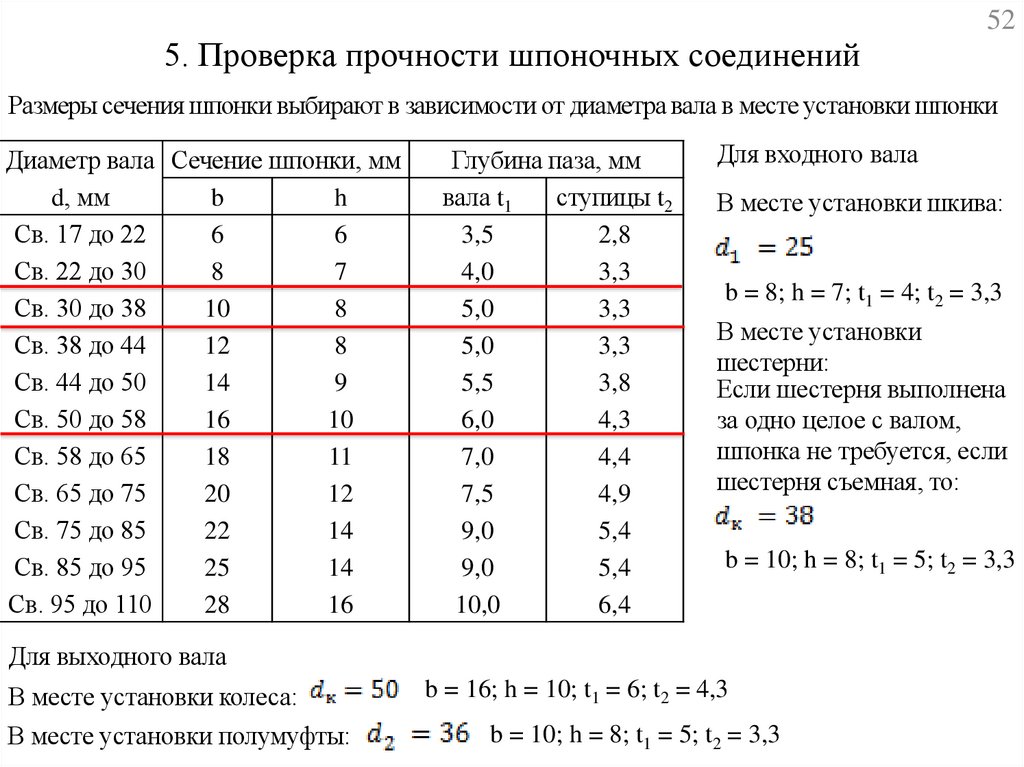
5. Проверка прочности шпоночных соединений
52
Размеры сечения шпонки выбирают в зависимости от диаметра вала в месте установки шпонки
Диаметр вала Сечение шпонки, мм
d, мм
b
h
Св. 17 до 22
6
6
Св. 22 до 30
8
7
Св. 30 до 38
10
8
Св. 38 до 44
12
8
Св. 44 до 50
14
9
Св. 50 до 58
16
10
Св. 58 до 65
18
11
Св. 65 до 75
20
12
Св. 75 до 85
22
14
Св. 85 до 95
25
14
Св. 95 до 110
28
16
Глубина паза, мм
вала t1
ступицы t2
3,5
2,8
4,0
3,3
5,0
3,3
5,0
3,3
5,5
3,8
6,0
4,3
7,0
4,4
7,5
4,9
9,0
5,4
9,0
5,4
10,0
6,4
Для входного вала
В месте установки шкива:
b = 8; h = 7; t1 = 4; t2 = 3,3
В месте установки
шестерни:
Если шестерня выполнена
за одно целое с валом,
шпонка не требуется, если
шестерня съемная, то:
b = 10; h = 8; t1 = 5; t2 = 3,3
Для выходного вала
В месте установки колеса:
В месте установки полумуфты:
b = 16; h = 10; t1 = 6; t2 = 4,3
b = 10; h = 8; t1 = 5; t2 = 3,3

53.

5. Проверка прочности шпоночных соединений
53
Рабочая длина шпонки
Для шкива
Для шестерни
Для колеса
Для полумуфты
Для шкива
Для шестерни
Для колеса
l, мм
10
12
14
16
18
20
22
25
28
32
36
40
45
50
56
63
70
80
90
100
110
125
140
160
180
200
220

54.

5. Проверка прочности шпоночных соединений
Часть шпонки, выступающую из вала, проверяют по напряжениям смятия
см
2Т i
см
zl p d i h t1
Тi – вращающий момент на валу, Н мм;
z – число шпонок (предварительно принимаем 1);
lp – рабочая длина шпонки, мм;
di – диаметр вала, мм;
h – высота шпонки, мм;
t1 – глубина паза вала, мм;
см = 70 МПа
Для шкива
Условие прочности выполняется
Для шестерни
Условие прочности выполняется
Для колеса
Условие прочности выполняется
54

55.

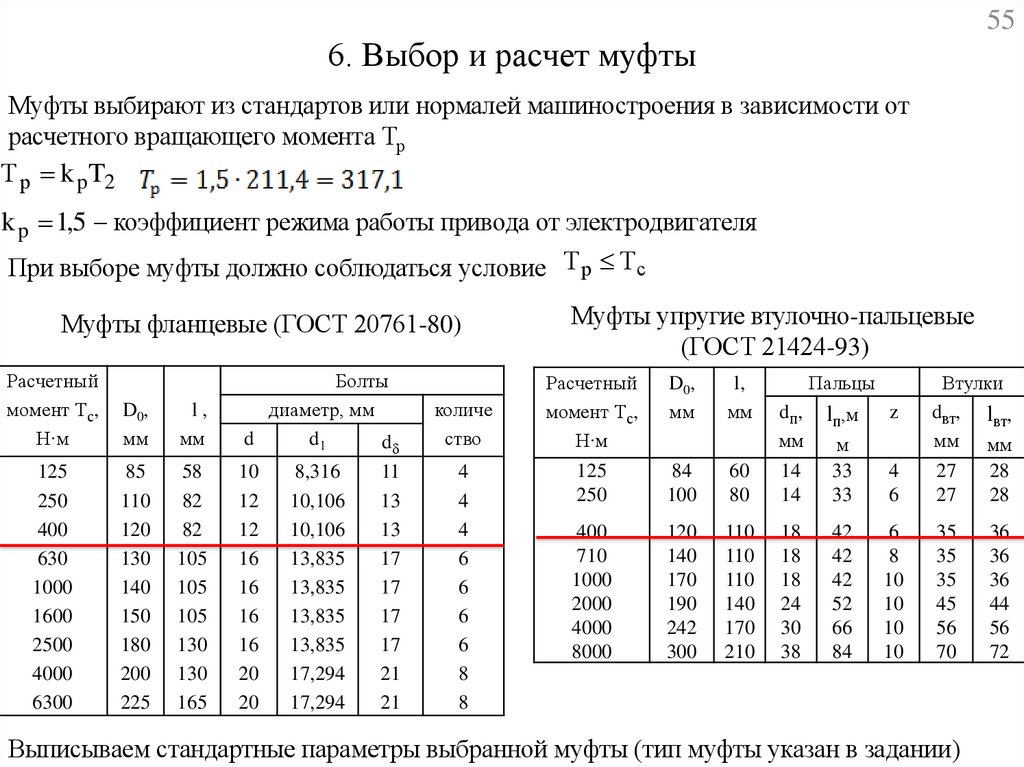
55
6. Выбор и расчет муфты
Муфты выбирают из стандартов или нормалей машиностроения в зависимости от
расчетного вращающего момента Тр
Т р k p T2
k p 1,5 коэффициент режима работы привода от электродвигателя
При выборе муфты должно соблюдаться условие Т р Т с
Муфты фланцевые (ГОСТ 20761-80)
Расчетный
момент Тс,
Н∙м
D0,
мм
l,
мм
Болты
диаметр, мм
d
d1
d
125
250
400
630
1000
1600
2500
4000
6300
85
110
120
130
140
150
180
200
225
58
82
82
105
105
105
130
130
165
10
12
12
16
16
16
16
20
20
8,316
10,106
10,106
13,835
13,835
13,835
13,835
17,294
17,294
11
13
13
17
17
17
17
21
21
количе
ство
4
4
4
6
6
6
6
8
8
Муфты упругие втулочно-пальцевые
(ГОСТ 21424-93)
Расчетный
момент Тс,
Н∙м
D0,
мм
125
250
84
100
60
80
400
710
1000
2000
4000
8000
120
140
170
190
242
300
110
110
110
140
170
210
l,
мм
Пальцы
lп,м
z
14
14
м
33
33
Втулки
dвт, lвт,
мм мм
4
6
27
27
28
28
18
18
18
24
30
38
42
42
42
52
66
84
6
8
10
10
10
10
35
35
35
45
56
70
36
36
36
44
56
72
dп,
мм
Выписываем стандартные параметры выбранной муфты (тип муфты указан в задании)

56.

6. Выбор и расчет муфты
Муфты фланцевые (ГОСТ 20761-80)
Муфты упругие втулочно-пальцевые
(ГОСТ 21424-93)
Болты в отверстия поставлены с зазором
p
10,4Tp
d12 D 0 fz
p
f = 0,15 – коэффициент трения
Условие прочности пальца на изгиб
и 90 МПа допускаемое
напряжение на изгиб для пальцев
р 0,5 т
т – предел текучести материала болта
(для стали Ст 3 т = 220 МПа; для стали 35
т = 320 МПа; для стали 45 т = 360 МПа)
56

57.

6. Выбор и расчет муфты
Муфты фланцевые (ГОСТ 20761-80)
Болты в отверстия поставлены без зазора
Условие прочности на срез
ср
8Т р
d б2 D 0 z
Муфты упругие втулочно-пальцевые
(ГОСТ 21424-93)
Резиновая втулка проверяется на смятие
cp
z’= z/2 число болтов, установленных
без зазора
ср 0,25 т
см 1,8 2,0 МПа – допускаемое
напряжение на смятие для резины
57

58.

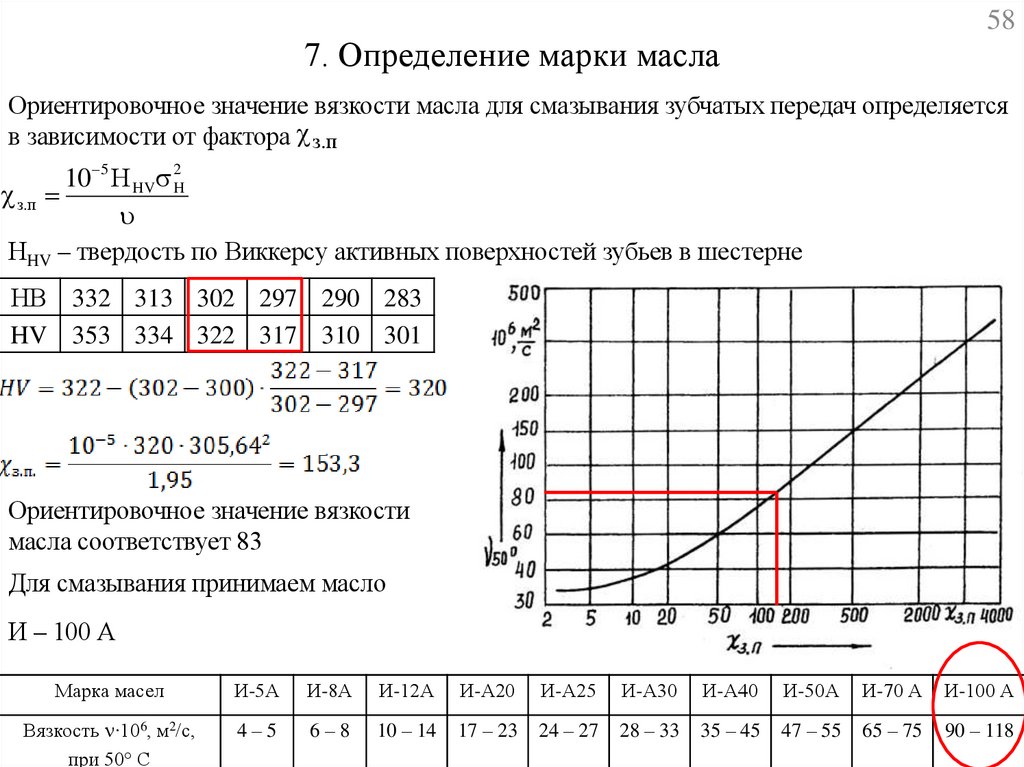
58
7. Определение марки масла
Ориентировочное значение вязкости масла для смазывания зубчатых передач определяется
в зависимости от фактора з.п
10 5 Н HV 2H
з .п
НHV – твердость по Виккерсу активных поверхностей зубьев в шестерне
НВ 332 313 302 297 290 283
HV 353 334 322 317 310 301
Ориентировочное значение вязкости
масла соответствует 83
Для смазывания принимаем масло
И – 100 А
Марка масел
И-5А
И-8А
И-12А
И-А20
И-А25
И-А30
И-А40
И-50А
И-70 А
И-100 А
Вязкость ∙106, м2/с,
при 50° С
4–5
6–8
10 – 14
17 – 23
24 – 27
28 – 33
35 – 45
47 – 55
65 – 75
90 – 118