Тригонометрическая форма записи комплексного числа

1.

ТЕМА
Тригонометрическая
форма записи
комплексного числа

2.

Комплексные числа, заданные парами
, называют чисто мнимыми
числами.
Для комплексных чисел существует
несколько форм записи:
алгебраическая форма записи,
тригонометрическая форма
записи и экспоненциальная
(показательная) форма записи.

3.

ТЕМА
Алгебраическая форма - это такая
форма записи комплексных чисел, при
которой комплексное число , заданное
,
парой вещественных чисел
записывается в виде
где использован символ
мнимой единицей.
, называемый

4.

Определение
Число называют вещественной
(реальной) частью комплексного
числа
и обозначают
.
Число называют мнимой частью
комплексного числа
обозначают
.
и

5.

Определения
Комплексные числа, у которых
, являются
вещественными числами.
Комплексные числа, у которых
, являются чисто
мнимыми числами.

6.

Сложение и вычитание
комплексных чисел

7.

Умножение комплексных чисел

8.

Определение
Два комплексных числа
и
у которых вещественные
части одинаковые, а мнимые части
отличаются знаком, называются
комплексно сопряжёнными
числами.

9.

Свойства комплексно
сопряжённых
чисел

10.

Определение
Модулем комплексного числа
называют вещественное
число, обозначаемое и
определенное по формуле

11.

Свойства модулей
комплексных чисел

12.

Деление комплексных
чисел

13.

Определение
Рассмотрим плоскость с заданной
на ней прямоугольной декартовой
системой координат
и
напомним, что радиус-вектором
на плоскости называют вектор,
начало которого совпадает с
началом системы координат.

14.

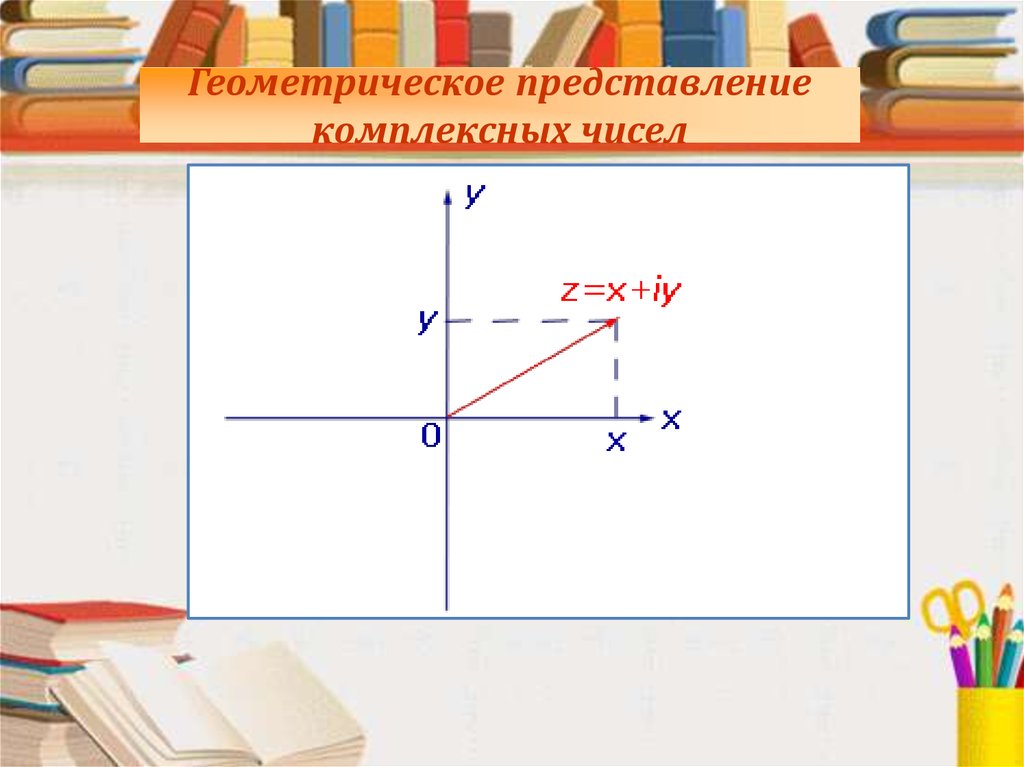
Определение
Назовем рассматриваемую
плоскость комплексной
плоскостью, и будем
представлять комплексное число
радиус–вектором с
координатами
.

15.

Геометрическое представление
комплексных чисел

16.

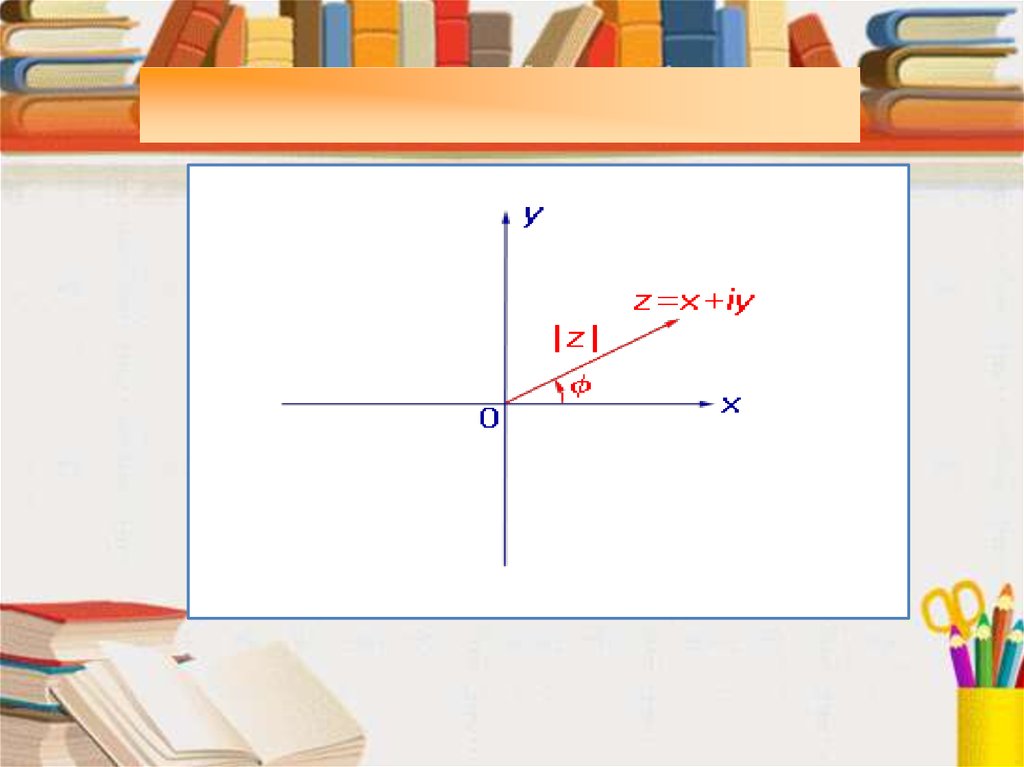
Определение
Аргументом комплексного числа
называют угол между положительным
направлением вещественной оси и
радиус-вектором .
Аргумент комплексного числа
считают
положительным, если поворот от
положительного направления
вещественной оси к радиус-вектору
происходит против часовой стрелки, и
отрицательным - в случае поворота по
часовой стрелке (см. рис.).

17.

18.

Определение
Поскольку аргумент любого комплексного
числа определяется с точностью до
слагаемого где - произвольное целое
число, то вводится, главное значение
аргумента, обозначаемое
и
удовлетворяющее неравенствам:
Тогда оказывается справедливым
равенство:

19.

Тригонометрическое
представление
комплексного числа
Если для комплексного числа
нам известны его модуль
и его
аргумент , то мы можем найти
вещественную и мнимую части по
формулам

20.

Тригонометрическая запись
колмплексного числа
Из формул вытекает, что любое
отличное от нуля комплексное число
может быть записано в виде

21.

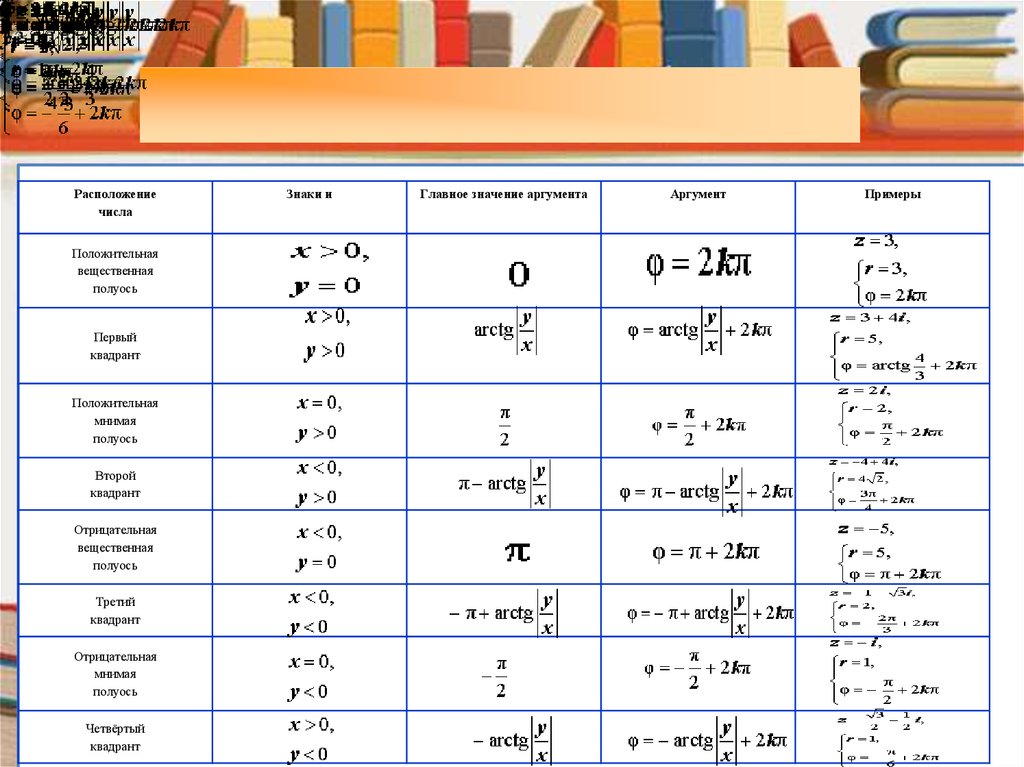
Расположение
числа
Положительная
вещественная
полуось
Первый
квадрант
Положительная
мнимая
полуось
Второй
квадрант
Отрицательная
вещественная
полуось
Третий
квадрант
Отрицательная
мнимая
полуось
Четвёртый
квадрант
Знаки и
Главное значение аргумента
Аргумент
Примеры

22.

Спасибо за работу на
уроке!