Похожие презентации:
Аксиоматическое определение вероятности события
1.
Аксиоматическое определение вероятностисобытия.
•Определение. Пусть Ω - пространство элементарных событий, u-
алгебра событий, А - событие, принадлежащее алгебре событий.
Вероятностью p(А) события А называется числовая функция,
p:A
p(А) каждому событию сопост. Действ. число
определенная для любого А из u и удовлетворяющая следующим
условиям (аксиомам):
A1) p(А) всегда неотрицательна (p(А)≥0)
A2)p(Ω) =1
A3)p(Σ Aк) = Σ p(Aк) - для несовместных событий A1, A2,…An (Ai Aj= Ø)
Вероятность суммы равна сумме вероятностей
2.
Свойства вероятности1.Вероятность противоположного события:
P(Ā)=1-P(A)
2.Формула сложения вероятностей (вероятность суммы двух совместных
событий):
P(A+B)=P(A)+P(B)-P(AB)
3.Монотонность вероятности:
Пусть событие А влечет за собой наступление B , тогда
P(B)≥P(A)
•Определение. Тройка (Ω,u,p) образует вероятностное пространство.
3. Условная вероятность. Независимость событий. Формулы сложения и умножения вероятностей. Формула полной вероятности, формула
Байеса.Схема Бернулли. Предельные теоремы — локальная, интегральная, теорема Пуассона. /Лек/
• Определение.
Условной вероятностью P(B/A)=PА(B)
называют
вероятность события В, вычисленную в предположении, что событие
А уже произошло.
Пример. В урне 3 белых и 3 черных шара, из урны дважды т по одному
шару, не возвращая их обратно. Найти вероятность извлечь черный
шар при втором испытании, если при первом испытании был
извлечен белый шар.
До-во
PА(B)=3/5=0,6.
P(W/A)= P(AW)/P(A) = P(A)/P(A) =1
P(B/A)=P(AB)/P(A) –
формула для вычисления условной вероятности. Проверить аксиомы
4. §8. Вероятность произведения событий
• Вероятность произведения событий А и В вычисляется по формулеР(АВ)=Р(А)Р(В/А)=Р(В)Р(А/В),
которую называют формулой умножения вероятностей.
Д-во
P(AB)/P(A) =P(B/A) домножить на P(A)
Замеч. Если число рассматриваемых событий больше двух, то
вероятность произведения событий следует вычислять,
последовательно применяя формулу умножения вероятностей.
Например, для трех событий
Р (АВС)=Р(АВ)Р(С/АВ)=Р(А)Р(В/А)Р(С/АВ)
5.
• Определение. События А и В называются независимыми еслиP(B/A)=P(B).
• Теорема. Если События А и В независимые события
Р(АВ)=Р(А)Р(В).
.д-во Р(АВ)=Р(А)Р(В/А)= Р(А)Р(В).
• Определение. События A1, A2,…An называются независимыми в
совокупности, если для любого
1≤k≤n и любого набора
различных между собой индексов i1,i2…ik имеет место равенство:
P(Ai ∩Ai …∩Ai )=P(Ai )P(Ai )…P(Ai )
1
2
k
1
2
k
Замечание. Если события независимы в совокупности, то они попарно
независимы, т.е. любые два события независимы. Обратное
утверждение, вообще говоря, неверно: из попарной независимости не
вытекает независимость в совокупности.
6.
Пример. Производится бросание двух игральных костей. А ={на первой кости выпало четное число очков}
В= {на второй кости выпало нечетное число очков} С = {сумма
очков четна}
Являются ли события попарно независимыми и независимыми в
совокупности?
Решение.
Р(АВС)=0; Р (А)=Р(В)=Р(С)=1/2; Р (АС)=Р(АВ)=Р(СВ)=1/4
Вывод.
События попарно независимы, но не являются независимыми в
совокупности.
7.
§8. Формула полной вероятности• Теорема. Пусть выполняются следующие условия:
события Н1, Н2,…..Нn – попарно несовместные события, т.е. Нi Нj = Ø
для любых i ≠ j;
события обладают конечными вероятностями Р(Нi) >0;
событие А наступает только вследствие наступления одного из
событий Нi, т.е. А = А Н1 + А Н2 +…..+ А Нn .
Тогда вероятность события А
вычисляется по формуле
P(A)= P(A/H1)P(H1)+ P(A/H2)P(H2)+…+ P(A/Hn)P(Hn)
(формула полной вероятности)
Доказательство. По А3 P(А) = P( А Н1 ) + P( А Н2 )+…..+ P( А Нn )
ДАЛЕЕ ПРИМЕНИТЬ ТЕОРЕМУ УМНОЖЕНИЯ P( А Н1 ) = P(A/H1)P(H1)
8.
Замечания.1.Если события Н1, Н2,…..Нn – попарно несовместные события и
Н1+Н2+….+Нn = Ω, то множество событий Н1, Н2,….., Нn называется
полной группой событий.
2.Часто события Н1, Н2,….., Нn называют гипотезами.
Пример.
На фабрике, изготавливающей болты, первая машина производит – 25%,
вторая – 35%, третья – 40% всей продукции. Брак в продукции
составляет 5%, 4% и 2% соответственно. Какова вероятность того, что
случайно выбранный болт оказался дефектным?A, H1,H2,H3
P(H1)=0,25;
P(H2)=0,35;
P(H3)=0,4
P(A/H1)=0,05;
P(A/H2)=0,04;
P(A/H3)=0,02
P(A)=0,25*0,05+0,35*0,04+0,40*0,02= 0,0345
9.
§9. Формула БайесаЕсли до опыта вероятности гипотез были Р(Нi), а в результате опыта
появилось событие A, то с учетом этого события "новые", т.е. условные
вероятности гипотез вычисляются по формуле Байеса:
P(Hk/A) = P(Hk)P(А/Hk) /P(A),
Где P(Hk) - априорная вероятность гипотезы Hk; P(Hk/A) - апостериорная
вероятность гипотезы Hk ;
P(А/Hk) - вероятность наступления события A при истинности гипотезы Hk;
P(A) - полная вероятность наступления события A.
Доказательство. Вычислим двумя способами вероятность P(HkA) :
P(HkA)= P(Hk) P(A/Hk)
и также P(AHk)= P(A) P(Hk/A)
Тогда
P(A) P(Hk/A) =P(Hk) P(A/Hk) . Далее делим на P(A) . Все.
Замечание. Формула Байеса позволяет «переставить причину и следствие»:
по известному факту наступления события вычислить вероятность того, что
оно было вызвано данной причиной.
10. Схема Бернулли
ОпределениеСхемой Бернулли называется
последовательность независимых
испытаний, в каждом из которых возможны
лишь два исхода — «успех» и «неудача»,
при этом «успех» в одном испытании
происходит с вероятностью p, а
«неудача» — с вероятностью q = 1 – p.
11. Теорема (формула Бернулли)
Обозначим через m число успехов в nиспытаниях схемы Бернулли. Тогда
Pn m C p q
m
n
m
n m
Доказательство
Событие A = {число успехов равно m}
означает, что в n испытаниях схемы
Бернулли произошло ровно m
успехов.
Рассмотрим один из благоприятных исходов:
у , у ,..., у , н, н,..., н
n m
m
12.
Посколькуиспытания
независимы,
вероятность такого элементарного исхода
равна
n m
m
p 1 p
Другие благоприятствующие событию A
элементарные исходы отличаются от
рассмотренного выше лишь расположением
m успехов на n местах. Есть ровно
m
n
способов расположить m успехов на n
местах.
C
13.
Поэтому событие A состоит изm
n
C
элементарных
исходов,
каждого из которых равна
вероятность
p 1 p
n m
m
т.е.
Pn m C p q
m
n
m
n m
.
14. Наивероятнейшее число успехов
В испытаниях схемы Бернулли наиболеевероятным числом успехов является
единственное число m0 = [np + p]
(целая часть), если число np + p не
целое;
a)
б)
два числа
m0 = np + p и m0' = np + p – 1, если
число np + p целое.
15. Пример
Вычислить вероятности всех возможныхзначений появления «герба» при 5
бросаниях монеты. Построить график
распределения этих вероятностей.
Решение
Число независимых испытаний n = 5.
Число успехов m = 0, 1, 2, 3, 4, 5.
Вероятность успеха в одном испытании p =
0,5.
16.
Pn m = C mn p m q n-mn = 5, m = 0, 1, 2, 3, 4, 5
0
5
1
4
1
1 1
P5 0 = C =
= 0.03125,
32
2 2
0
5
5
1 1
P5 1 = C =
= 0.15625,
32
2 2
1
5
2
3
10
1 1
P5 2 = C =
= 0.31250, и т. д.
32
2 2
2
5
17.
Наивероятнейшее число успехов:Вычисляем np + p = 5∙1/2 + ½ = 3.
Это целое число, поэтому
m0 = np + p = 3 и m0' = np + p – 1 = 2.
Самые большие (и равные между собой)
вероятности у двух и трех появлений
герба.
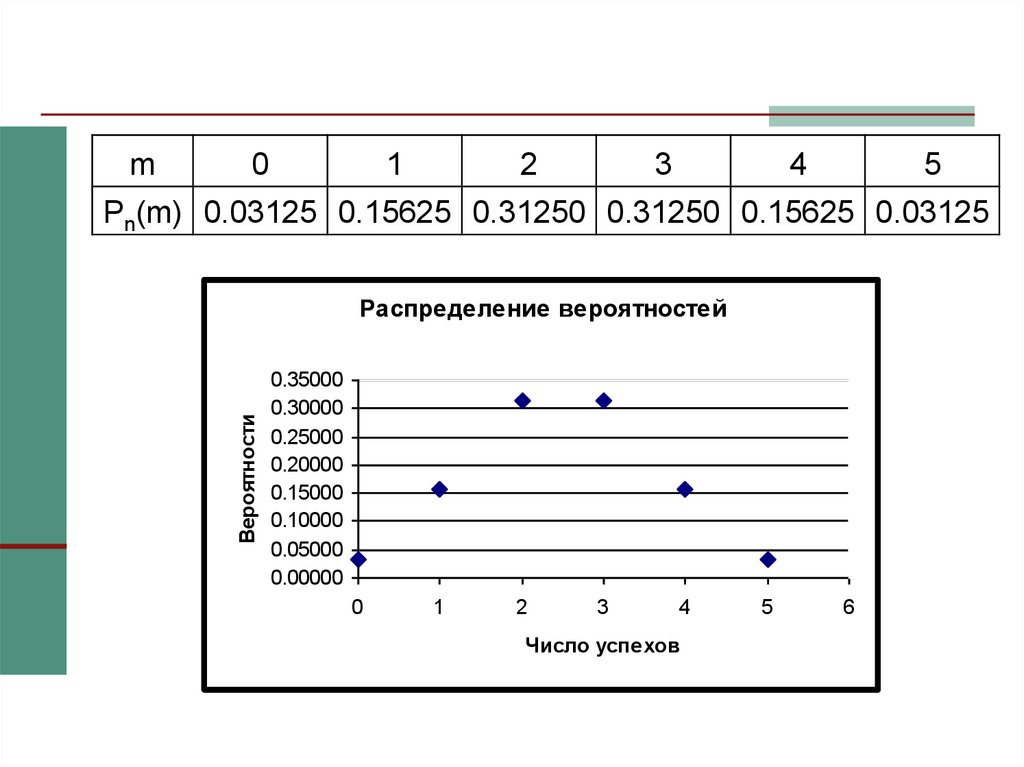
18.
m0
1
2
3
4
5
Pn(m) 0.03125 0.15625 0.31250 0.31250 0.15625 0.03125
Вероятности
Распределение вероятностей
0.35000
0.30000
0.25000
0.20000
0.15000
0.10000
0.05000
0.00000
0
1
2
3
4
Число успехов
5
6
19. Еще один пример
Вероятность сдать экзамен равна 0,8.Найти наивероятнейшее число студентов,
сдавших экзамен в группе из 30 человек.
Решение.
Вычисляем np + p = 30∙0,8 + 0,8 = 24,8.
Это не целое число, поэтому
m0 = [24,8] = 24.
20. Полиномиальная схема
ОпределениеПолиномиальной схемой называется
последовательность n независимых
одинаковых испытаний, в каждом из которых
возможны k исходов
k
A1 , A2 ,
, Ak ,
Ai ,
i 1
при этом вероятность любого исхода в каждом
испытании постоянна,
P Ai pi ,
1, n , i 1, k,
k
p 1
i 1
i
21. Полиномиальная формула
Pn m1 , m2 ,...mkсобытие A1 произошло ровно m1 раз,
P
событие A произошло ровно m раз
k
k
n!
m1
m2
p1 p2
m1 ! m2 ! mk !
p .
mk
k
22. Пример
Человек с вероятностью 0,2 оказываетсябрюнетом, с вероятностью 0,4 —шатеном, с
вероятностью 0,3 — блондином и с
вероятностью 0,1—рыжим. Выбирается наугад
группа из шести человек. Найти вероятность
того, что в составе группы два брюнета, один
шатен и три блондина.
P6 2,1,3,0
6!
0, 22 0, 41 0,33 0,10.
2! 1! 3! 0!!
23. Гипергеометрические испытания
Пусть из совокупности n предметов, средикоторых n1 предметов первого вида и n2
предметов второго вида (n1 + n2 = n)
производится выборка без возвращения m
предметов, 1 m n.
Вероятность того, что в выборке будет m1
предметов первого вида и m2 предметов
второго вида (m1 + m2 = m), согласно
классическому определению вероятности,
выражается формулой
24. Гипергеометрические вероятности
Pn1 ,n (m1 , m)C C
m1
n1
m2
n2
m
n
C
Данные испытания являются зависимыми.
25. Пример
В урне 6 белых и 5 черных шаров.Из урны вынимают наугад 5 шаров. Найти
вероятность, что два из них будут белыми,
а три – черными.
Решение:
n( A) C С
2
6
n C
5
11
3
5
C C
P( A)
.
5
C11
2
6
3
5
26. Теорема
Пусть n и n1 так, чтоn1
p, 0 p 1
n
Тогда
Pn1 ,n (m1 , m) Pm (m1 ).
27. Доказательство
Pn1 ,n m1 , mCnm11 Cnm22
C
m
n
m! n m !
n1!
n2 !
n!
m1! n1 m1 ! m2 ! n2 m2 !
n1 n1 1 n1 m1 1 n2 n2 1 n2 m2 1
m!
n n n n
n n n n n
n
n n 1 n m 1
m1! m2 !
n n n n
n
m!
m
p m1 1 p 2 Pm m1
m1! m2 !
28. Предельные теоремы для схемы Бернулли
При числе испытаний, превышающем 20,вычисление точного значения Pn(m)
затруднительно. В этих случаях применяют
приближенные формулы, вытекающие из
предельных теорем.
Различают два случая:
когда р мало, используют приближение
Пуассона,
когда р не мало (и не очень близко к единице),
справедливо приближение Муавра –Лапласа.
Существует область, в которой возможно
применение обоих приближений.
29. Теорема Пуассона
Если n , р 0 так, что np , 0 < < ,то
для
любого
фиксированного
m N
справедливо:
Pn m C p 1 p
m
n
m
n m
p m
e
m
m!
30. Доказательство
Пусть np = n. ТогдаPn m C p 1 p
m
n
n m
m
n!
n n
1
n m ! m! n n
m
n m
n n 1 n m 1 n n
1
m!
n
n
m
n m
n 1 2 m 1 n
1 1 1 1
1
m!
n n n
n
n
m
n
n
m
31. При n , n= np
При n , n= npn
1 e ,
n
1
2
m 1
1 1, 1 1, , 1
1,
n
n
n
n
n
1
n
m
1.
32.
Следовательно,Pn m C p 1 p
m
n
m
n m
p m
e
m
m!
33. Приближенная формула Пуассона
Pn m p me
m
m!
где = np. Приближенную формулу
Пуассона применяют при
n > 30,
р < 0.1,
0.1 < = np < 10.
34. Пример (дни рождения)
Какова вероятность, что среди 500случайно выбранных людей ни один не
родился 1 января ?
Решение
По формуле Бернулли
P500 0 C p 1 p
0
500
0
500
364
365
500
0.2537
35.
По приближенной формуле Пуассона1
np 500
1.3699
365
0e
P500 0
e 1.3699 0.2541
0!
36. Предельная теорема Муавра –Лапласа
Если при n и постоянном р, не равном 0или 1, величина
m np
xm
npq
ограничена так, что – < а хт b < + , то
Pn m
xm
1
1 O
,
npq
n
1
где x
e
2
x2
2
.
37.
Доказательство этой теоремы основано наприменении формулы Стирлинга
n! n e
n
n
2 n e
1
O
n
38. Локальная приближенная формула Муавра –Лапласа
Локальная приближенная формула Муавра –Лапласа
Pn m
x m
npq
m np
xm
npq
Локальную приближенную формулу Муавра –
Лапласа применяют при
n > 30, 0.1 p 0.9, nрq > 9.
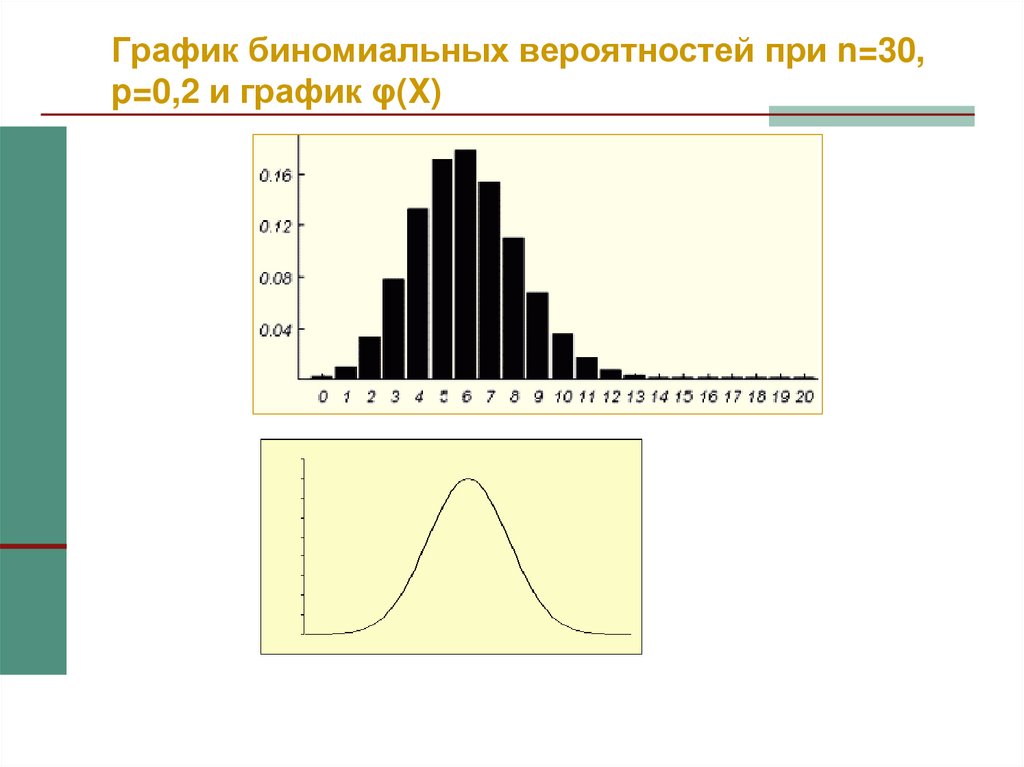
39. График биномиальных вероятностей при n=30, p=0,2 и график φ(X)
40. Интегральная предельная теорема Муавра –Лапласа
При n и постоянном р, не равном 0 или 1,m np
lim p x1
x 2
n
npq
x2
1
e
2 x1
x
x2
2
dx x 2 x1 ,
x
1
e
2
t2
2
x
dt t dt
41. Доказательство
m npp x1
x 2
npq
p x1 npq np m x 2 npq np
x 2 npq np
xm x2
pn m pn m
m x1 npq np
x m x1
m np
xm
npq
42. По локальной предельной теореме
xm x2p m
x m x1
n
In
xm x2
1
e
2 xm x1
xm x2
1
e
2 xm x1
x2
2
x2
2
1
1 n In An
npq
xm x2
1
npq xm x1
1
x m
npq
43.
m npm 1 np m np
1
xm
, xm
npq
npq
npq
npq
xm x2
x2
x m x1
x1
In xm xm x dx
44.
xm x2An xm xm n
x m x1
xm x2
C
An xm xm n
In
n
x m x1
45. при n An 0
при nAn 0
m
np
lim p x1
x 2
n
npq
lim I n An
n
x2
x dx
x1
x2
1
e
2 x1
x2
2
dx x 2 x1 .
46. Интегральная приближенная формула Муавра –Лапласа
m nplim p x1
x 2 x 2 x1 ,
n
npq
x
x
1
e
2
t2
2
x
dt t dt
Интегральную приближенную формулу Муавра –
Лапласа применяют при
n > 30, 0.1 p 0.9, nрq > 9.
47. Следствия
b npa np
p a m b
npq
npq
m
n
n
1 p
p 1 2 2 p
n
pq
pq
m
n
n
1
p 1 p 2 2
n
pq
pq
48. Свойства функции (x)
Свойства функции (x)x x
1
0
0.3989
2
lim x 0
x
4 0.001
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
49. Свойства функции Ф(x)
x x 1lim x 0
x
lim x 1
x
1
0
2
3.8 0.9999
3.8 0.0001
1
2
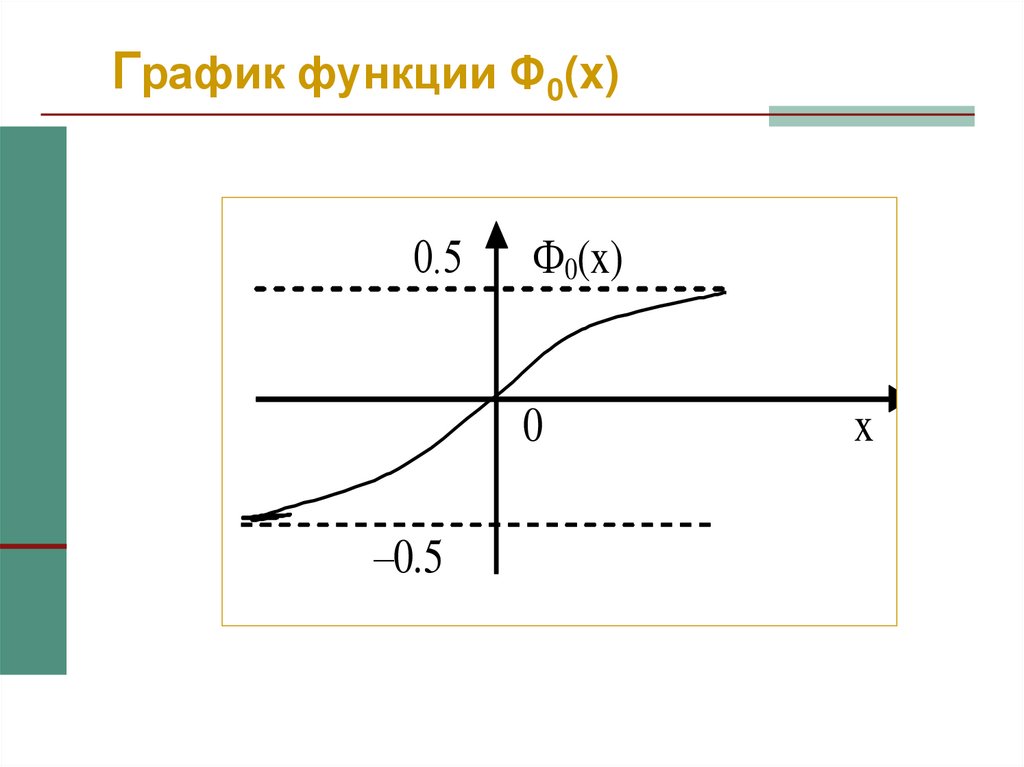
50. Функция Лапласа Φ0(x).
Вместо Φ(x) часто используют функциюЛапласа Φ0(x).
0 x
x
1
e
2 0
t2
2
1
( x) 0 ( x)
2
dt .
51. График функции Φ0(x)
0.5Ф0(x)
0
–0.5
x
52. Замечания
0 x2 0 x1 x2 x1 ,поэтому в формулах может
использоваться как Φ(x), так и Φ0(x).
Значения функций находят в таблицах.
53. Пример
Вероятность рождения мальчика p = 0,5.Найти вероятность того, что в группе из 100
новорожденных мальчиков не меньше 60.
Решение.
p 60 m 100
100 100 0,5
60 100 0,5
100 0,5 0,5
100 0,5 0,5
50
10
(10) (2) 1 0,98=0,02.
25
25















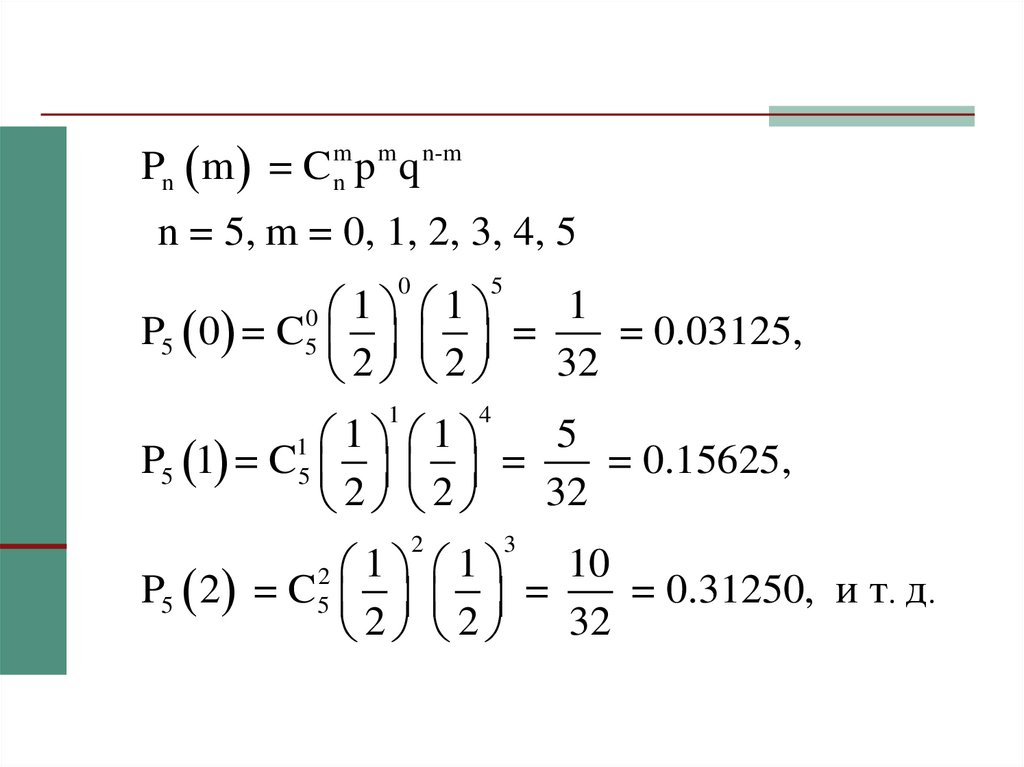













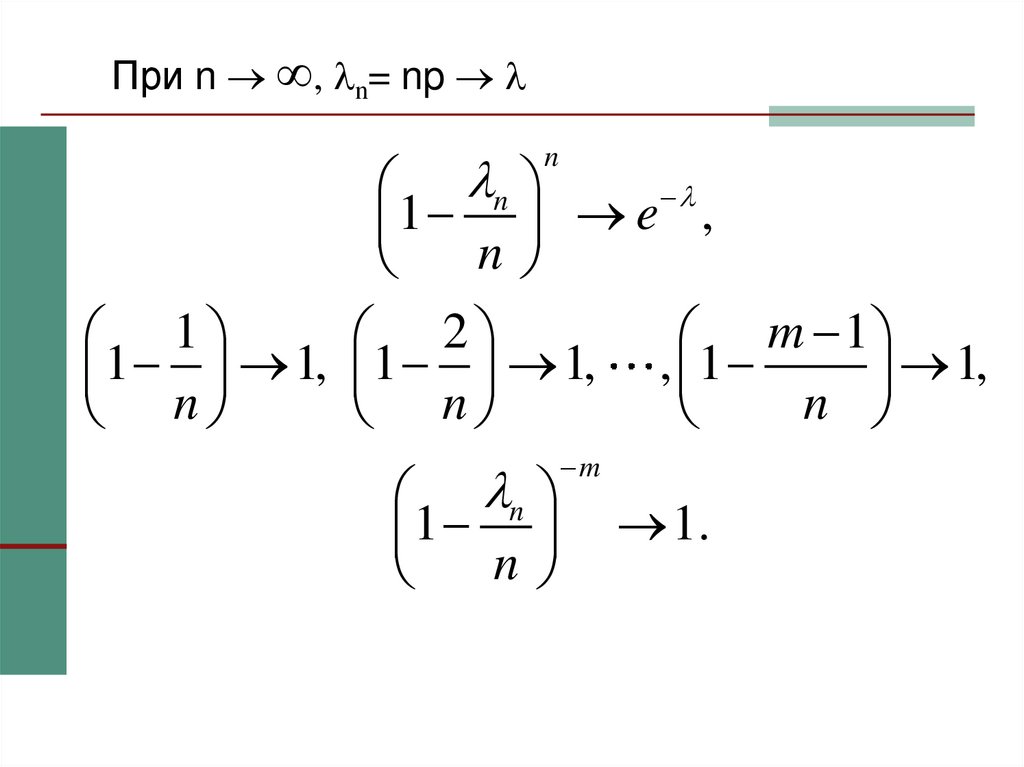











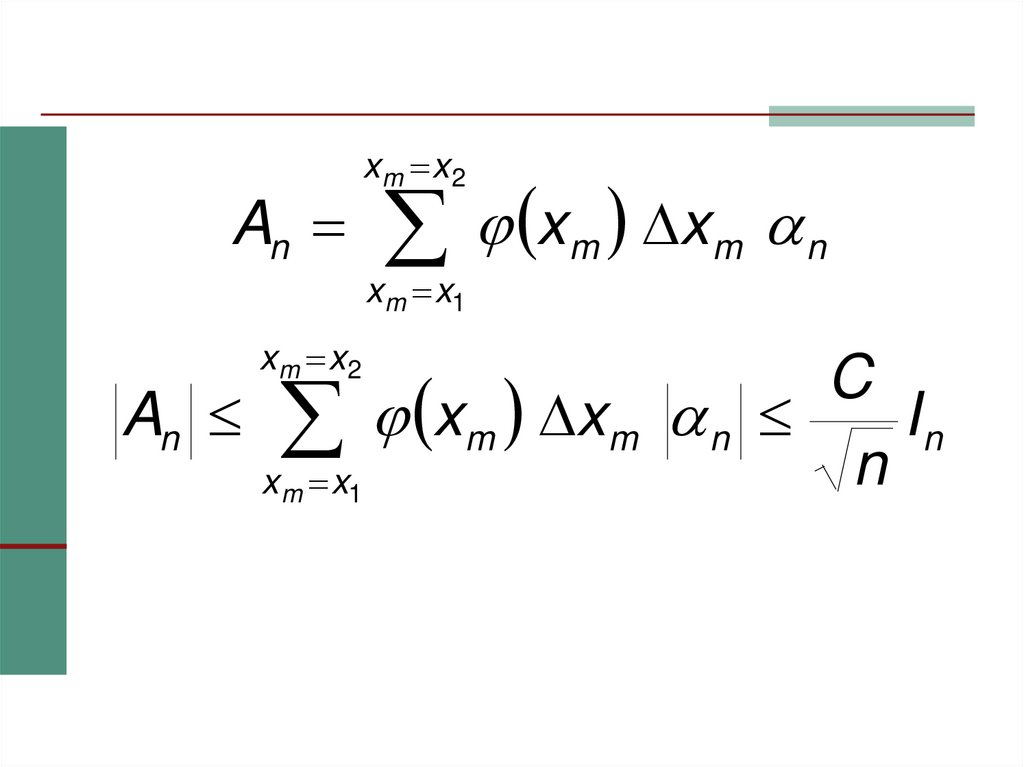
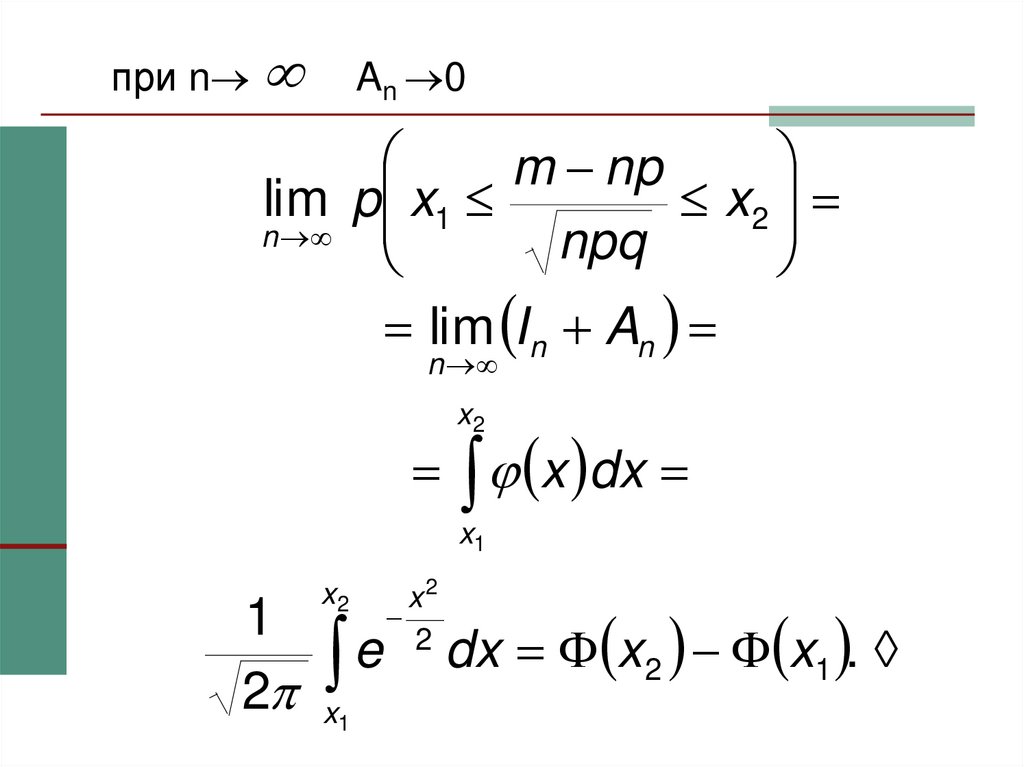








 Математика
Математика








