Лекция №3 Электромагнитные волны

1.

Дистанционный курс общей физики НИЯУ МИФИ
Основы волновой оптики
ЛЕКЦИЯ № 3
ТЕМА: ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
2023 г.
Лектор: Зав. каф. общей физики НИЯУ МИФИ
д.ф.-м.н., проф., заслуженный деятель науки РФ
КАЛАШНИКОВ Н.П.
1

2.

ЛЕКЦИЯ № 3
Содержание:
§ .1 Уравнения Максвелла.
§ .2 Волновое уравнение для электромагнитных волн
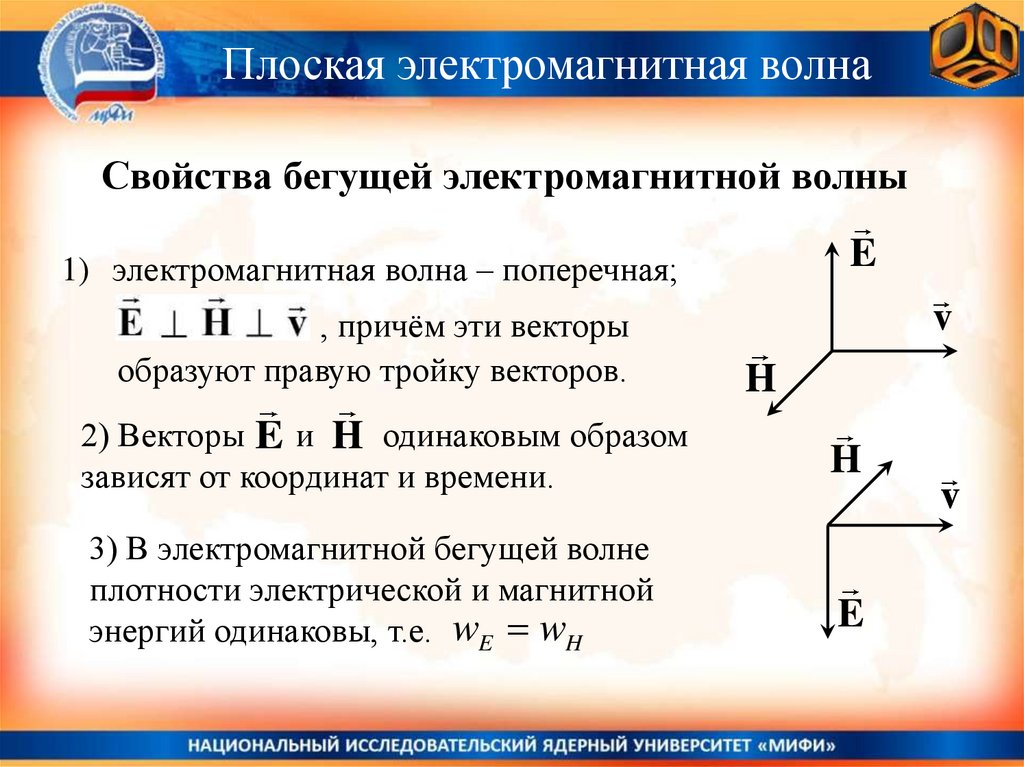
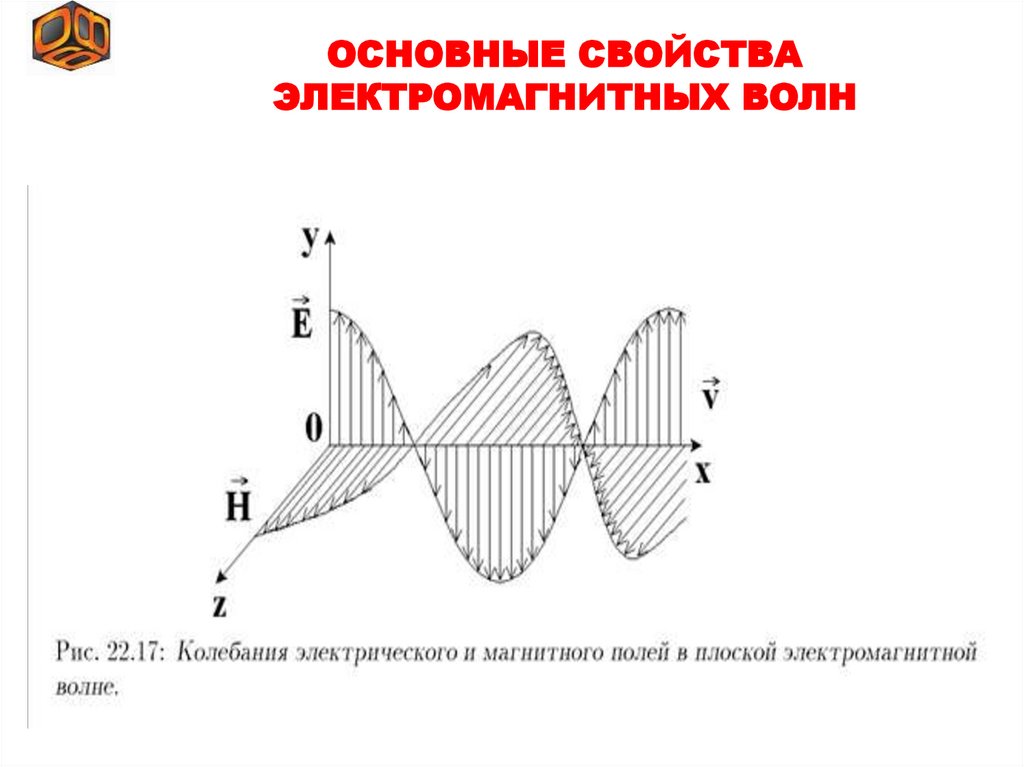
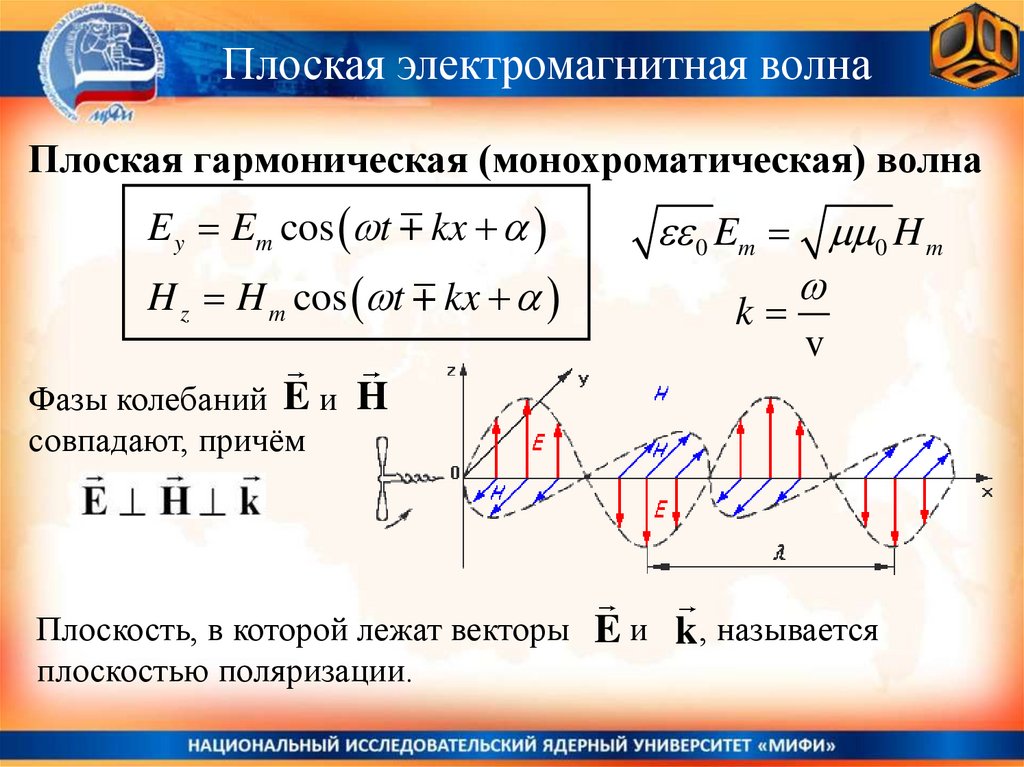
§ .3 Основные свойства электромагнитных волн
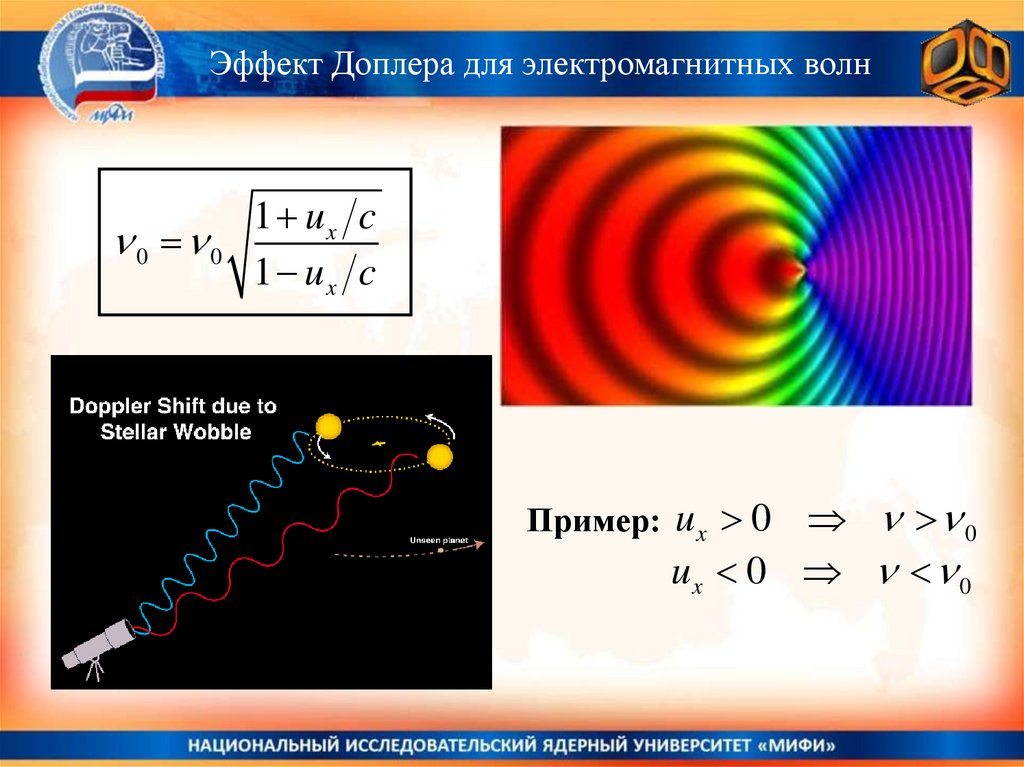
§ .4. Эффект Доплера для электромагнитных волн.
§ .5. Иллюстративный пример.
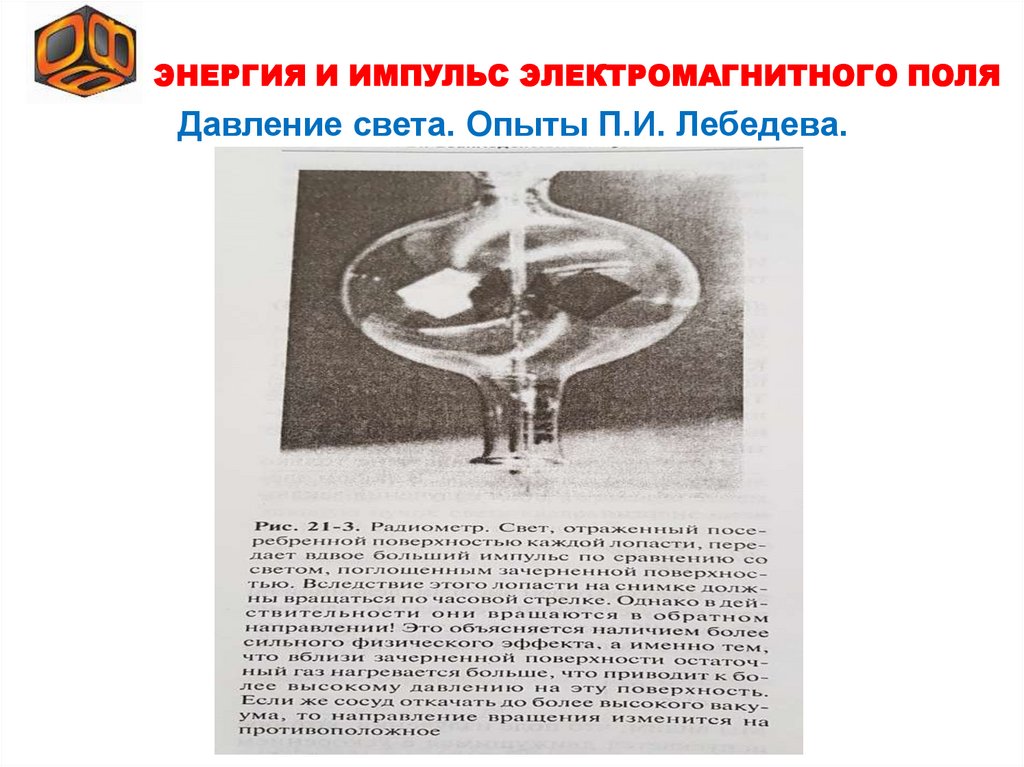
§ .6. Энергия и импульс электромагнитного поля.
§ .7. Давление света.
§ .8. Законы оптики и уравнения Максвелла.
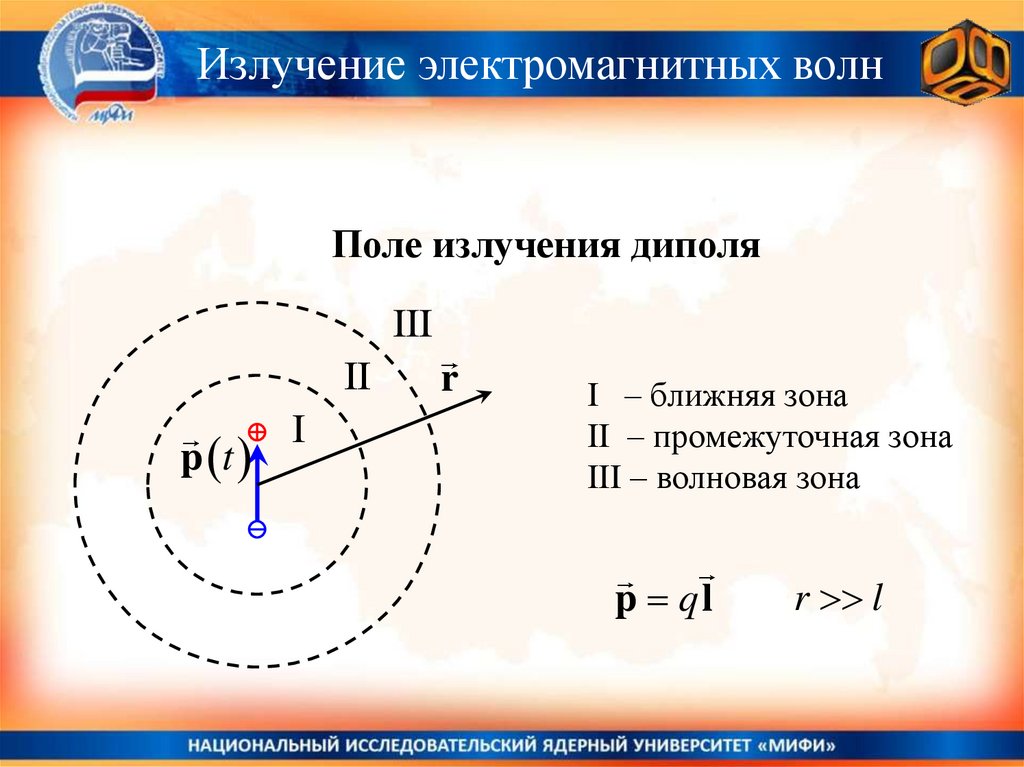
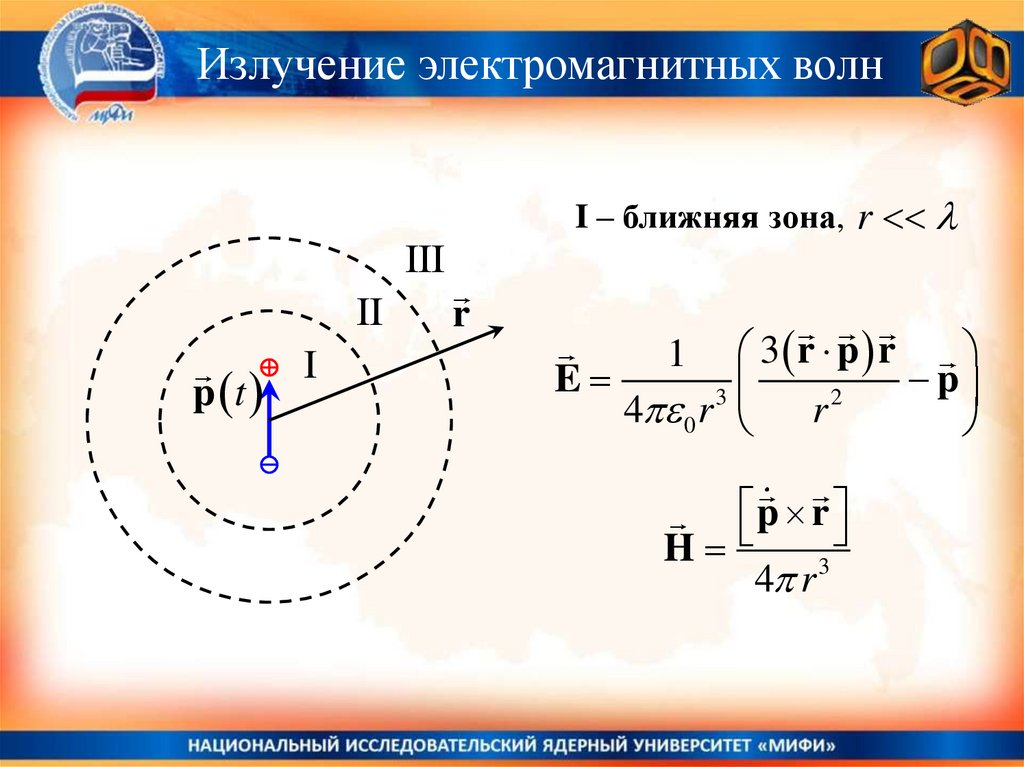
§ .9.Механизм электромагнитного излучения.
§ .10. Законы оптики и уравнения Максвелла.
§ .11. Дипольное излучение.
§ .12. Излучение равномерно движущегося заряда.
§ .13. Излучение Вавилова-Черенкова.
§ .14. Переходное излучение.

3.

Список рекомендованной литературы
• Калашников Н.П. и Смондырев М.А. ОСНОВЫ
ФИЗИКИ. т.2. –М.: Лаборатория знаний.
Бином. 2017. – 606с. Учебник для высшей
школы.
Часть V. Основы волновой оптики
Глава 32. §§ 32.1 – 32.11

4.

Уравнения Максвелла в локальной форме
Основные уравнения электромагнитного поля
в неподвижных средах.
B
E
t
D
D
H jпров
t
B 0
стор
Джеймс Клерк
Ма́ксвелл,
1831- 1879

5.

Уравнения Максвелла
Свойства уравнений Максвелла
1. Уравнения выполняются во всех инерциальных системах отсчёта.
Они являются релятивистски инвариантными.
2. Уравнения линейные – отражение принципа суперпозиции для
магнитных и электрических полей.
3.Уравнения содержат известные законы электродинамики: закон
Кулона, закон Био-Савара-Лапласа, уравнение непрерывности и т.п.
4. Уравнения не симметричны относительно векторов E и B.
5. Из уравнений Максвелла вытекает возможность
распространения электромагнитных волн в средах и в вакууме.

6.

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Уравнения Максвелла.
Любой колебательный контур излучает энергию.
Изменяющееся электрическое поле возбуждает в
окружающем пространстве переменное магнитное
поле, и наоборот. Математические уравнения,
описывающие связь магнитного и электрического
полей, были выведены Максвеллом. Запишем
уравнения Максвелла в дифференциальной форме
для случая, когда отсутствуют электрические
заряды (ρ=0) и токи (Ԧ