Алгебра логики

1.

АЛГЕБРА ЛОГИКИ
Алгебра логики (алгебра высказываний) — раздел
математической логики, в котором изучаются логические
операции над высказываниями.

2.

Высказывания
Высказывание — это утверждение, про которое можно
ввопределённо сказать, истинно оно или ложно.
1. Есенин – известный художник
2. Клавиатура – средство ввода информации
3. Черепаха весит больше мыши?
4. Пора домой!
5. Бит – наименьшая единица измерения информации
6. Число 5 в двоичной системе = 1012
7. Информатика – интересный предмет

3.

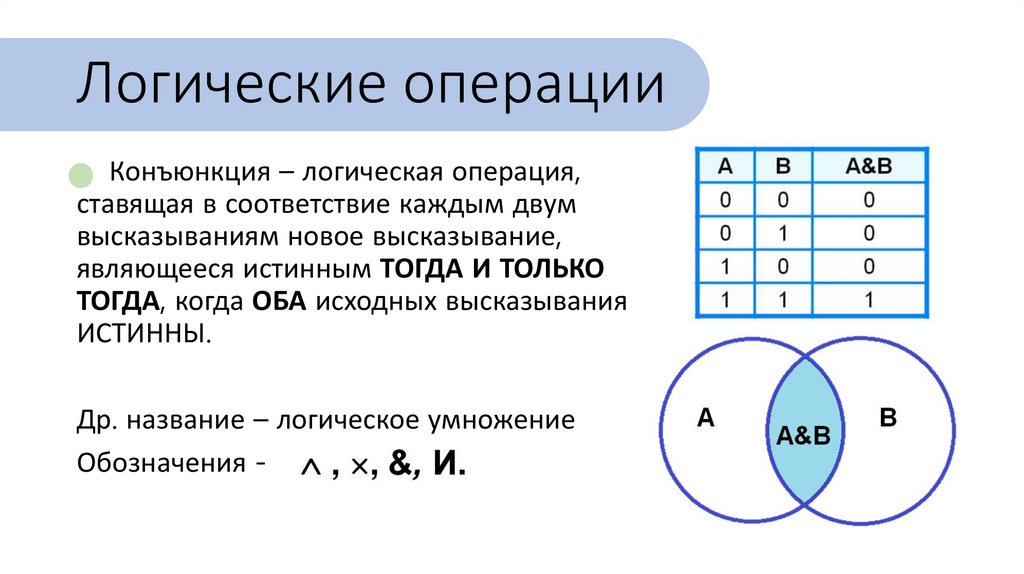
Логические операции
Конъюнкция – логическая операция,
ставящая в соответствие каждым двум
высказываниям новое высказывание,
являющееся истинным ТОГДА И ТОЛЬКО
ТОГДА, когда ОБА исходных высказывания
ИСТИННЫ.
Др. название – логическое умножение
Обозначения -

4.

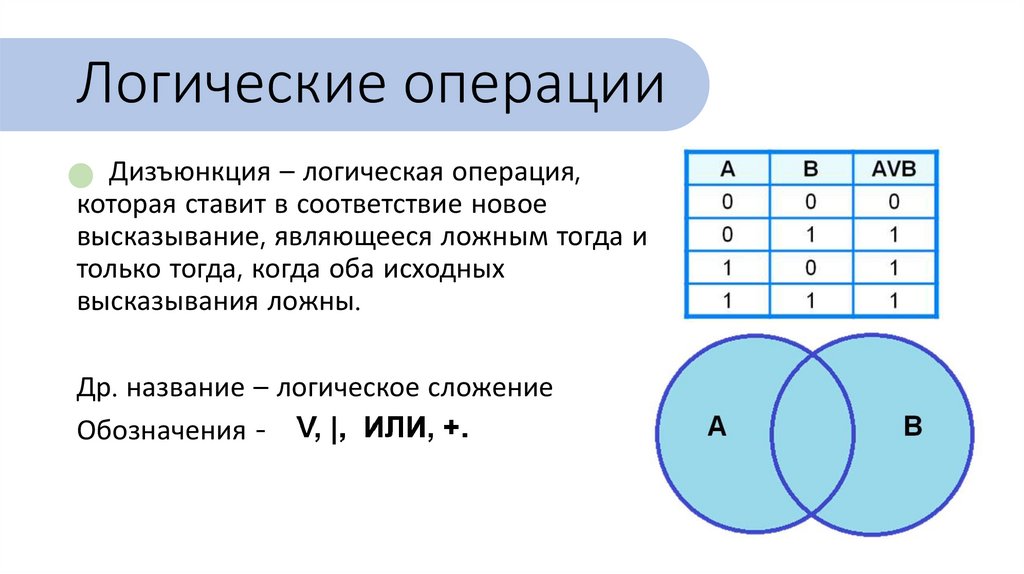
Логические операции
Дизъюнкция – логическая операция,
которая ставит в соответствие новое
высказывание, являющееся ложным тогда и
только тогда, когда оба исходных
высказывания ложны.
Др. название – логическое сложение
Обозначения -

5.

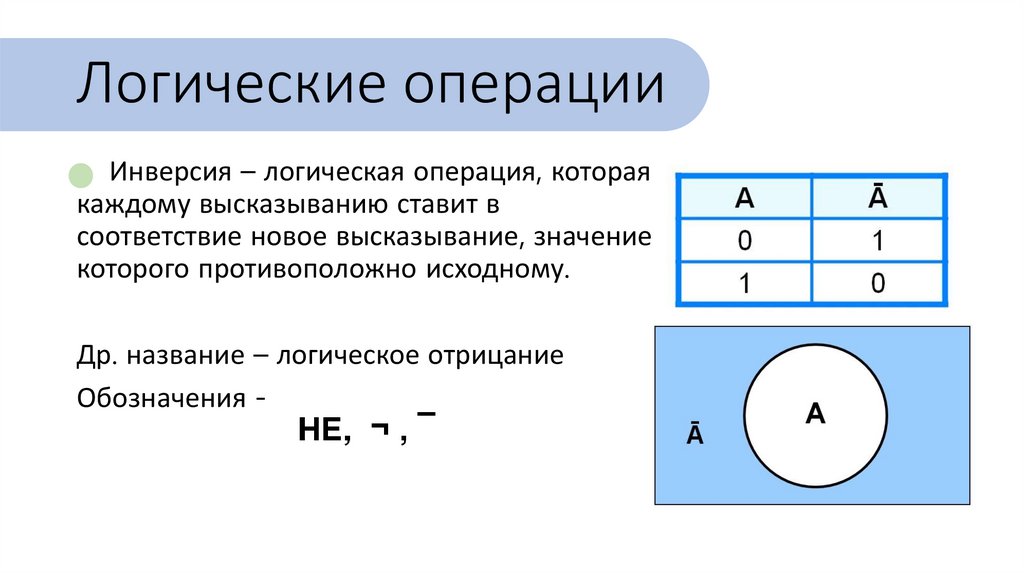
Логические операции
Инверсия – логическая операция, которая
каждому высказыванию ставит в
соответствие новое высказывание, значение
которого противоположно исходному.
Др. название – логическое отрицание
Обозначения -

6.

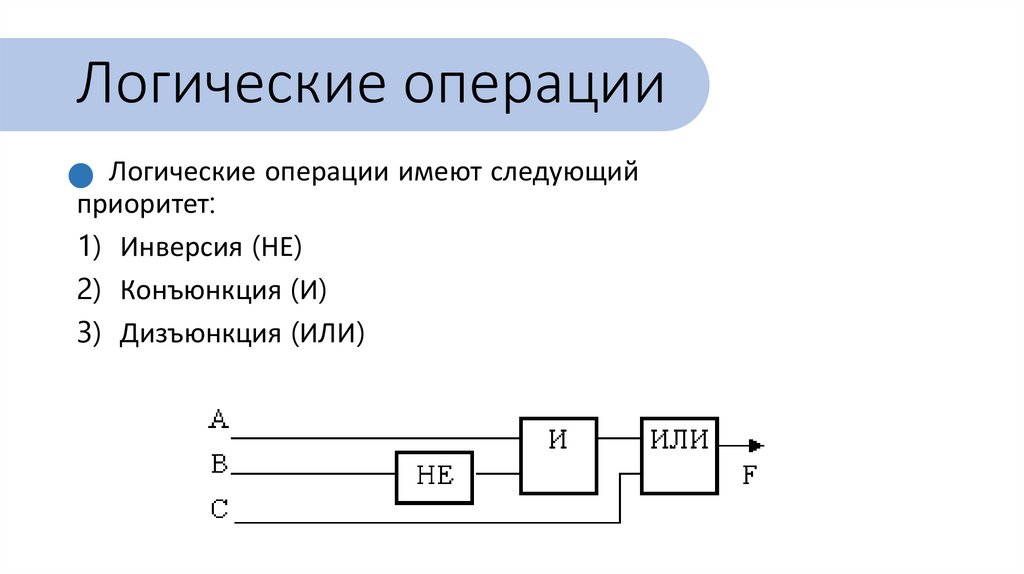
Логические операции
Логические операции имеют следующий
приоритет:
1) Инверсия (НЕ)
2) Конъюнкция (И)
3) Дизъюнкция (ИЛИ)

7.

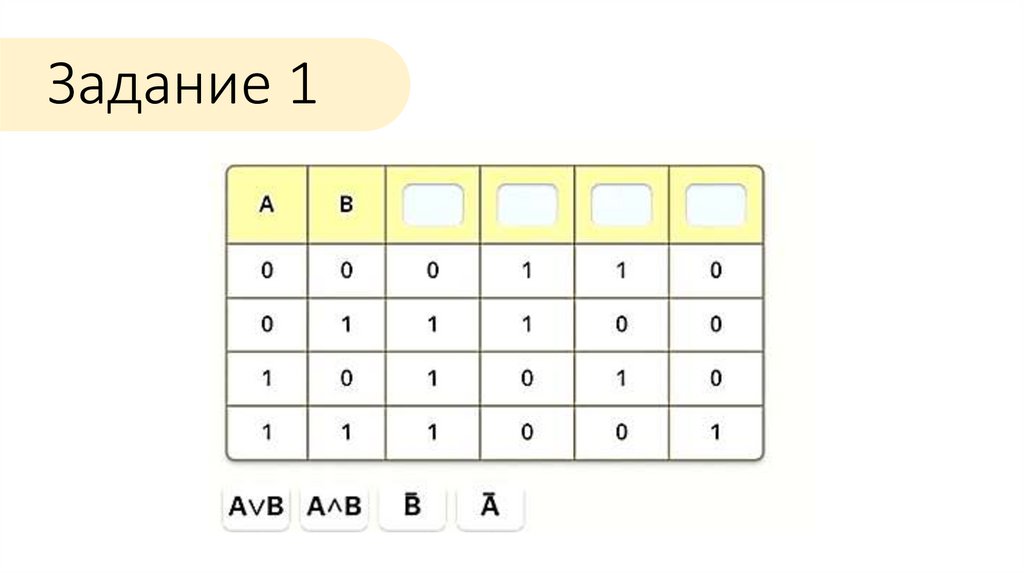
Задание 1

8.

Логические операции
Импликация – логическая операция,
образующая сложное высказывание, ложное
тогда и только тогда, когда первое исходное
высказывание истинно, а второе — ложно.
Оборот речи – ЕСЛИ, ТО
•Утверждение A: "Я поставил будильник на 7
утра."
•Утверждение B: "Я проснулся в 7 утра."
•Импликация A → B: "Если я поставил будильник
на 7 утра, то я проснусь в 7 утра."

9.

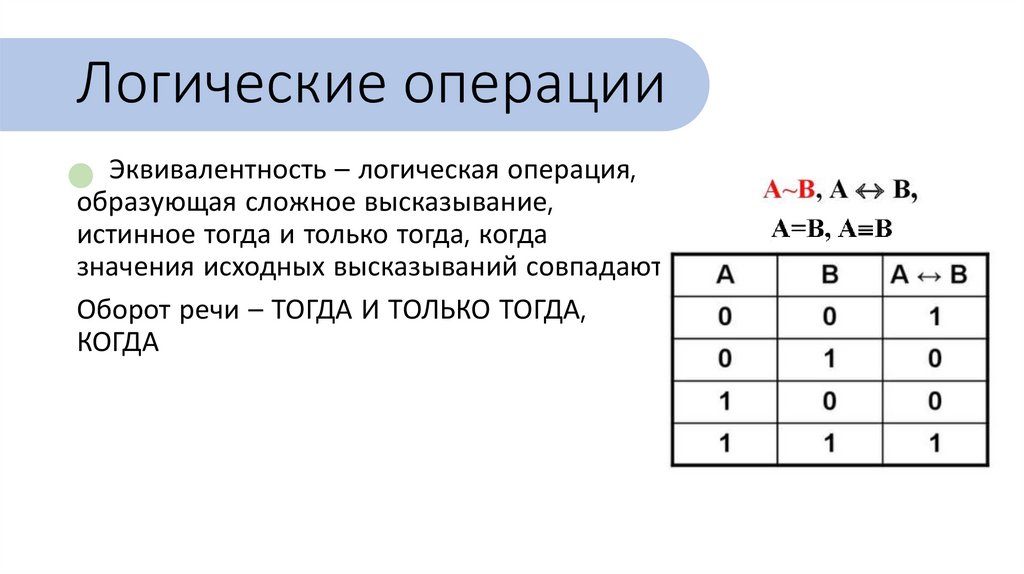
Логические операции
Эквивалентность – логическая операция,
образующая сложное высказывание,
истинное тогда и только тогда, когда
значения исходных высказываний совпадают.
Оборот речи – ТОГДА И ТОЛЬКО ТОГДА,
КОГДА

10.

Задание 2

11.

Задание 3
Составить таблицу истинности сложного логического
выражения F = НЕ (A) & (B+C)

12.

Задание 4
Составить таблицу истинности сложного логического
выражения F = НЕ [А & НЕ(В) ИЛИ С]

13.

Домашнее задание на 25.03
1. Выучить определения, обозначения логических операций, таблицы истинности
2. Составить таблицу истинности сложного логического выражения (выбрать два выражения из
левого и два выражения из правого столбцов) : ВСЕГО ВЫЙДЕТ 4 ТАБЛИЦЫ!