Похожие презентации:
Колебательные состояния многоатомных молекул. Классическая теория
1. Колебательные состояния многоатомных молекул Классическая теория
Потенциальная и кинетические энергии для малых колебаний:1 n
U k ij qi q j
2 i , j 1
Линейное преобразование:
1 n
T aij q i q j
2 i , j 1
и
n
q1 C1k Qk
k 1
.......................
n
q n C nk Qk
k 1
1 n
T t k Qk2 .
2 k 1
В новых координатах:
1 n
U u k Qk2
2 k 1
Для нормальных координат:
Qk Qk 0 cos( 2 v k t k ) , где
и
1 uk
,
2 t k
2. Зависимость от времени смещений атомов
Зависимость от времени исходных координат q1 , q 2 ...q n :q1 C11Q10 cos(2 1t 1 ) + …….+ C1n Qn 0 cos(2 n t n )
...............................................................................................
q n C n1Q10 cos(2 1t 1 ) + …….+ C nn Qn 0 cos( 2 n t n )
Частные решения:
q1(1) C11Q10 cos( 2 1t 1 )
.......................................
q n(1) C n1Q10 cos(2 1t 1 )
или
q1( k ) C1k Qk 0 cos( 2 k t k )
................................................
q n( r ) C nk Qk 0 cos( 2 k t k )
Частным решениям уравнений соответствуют одновременные изменения всех
координат с одной частотой и одной фазой
3. Анализ нормальных координат. I
В матричном виде:1 n
1
U k ij qi q j {q}F q
2 i , j 1
2
1 n
1
T aij q i q j { p}G p
2 i , j 1
2
где {} – строчная матрица,
- столбцовая матрица, F [k ij ] ( F [ f ij ] ),
G [ ij ] - квадратные симметрические матрицы.
GF λE 0
Вековое уравнение:
или в развернутой форме:
d11
d12
...
d1n
d 21
d 22
...
d 2n
..................................................
=0
..................................................
d n1
d n2
...
d nn
4. Анализ нормальных координат. II
nгде d ij ik f kj - элементы матрицы произведения D GF . Оно имеет n
k 1
корней
k 4 2 2k ,
т.е. дает n частот колебаний.
Полное колебательное уравнение:
GF L L 0 ,
L – полная матрица нормированных форм колебаний (матрица линейного
преобразования нормальных координат q L Q ),
– диагональная матрица всех корней k .
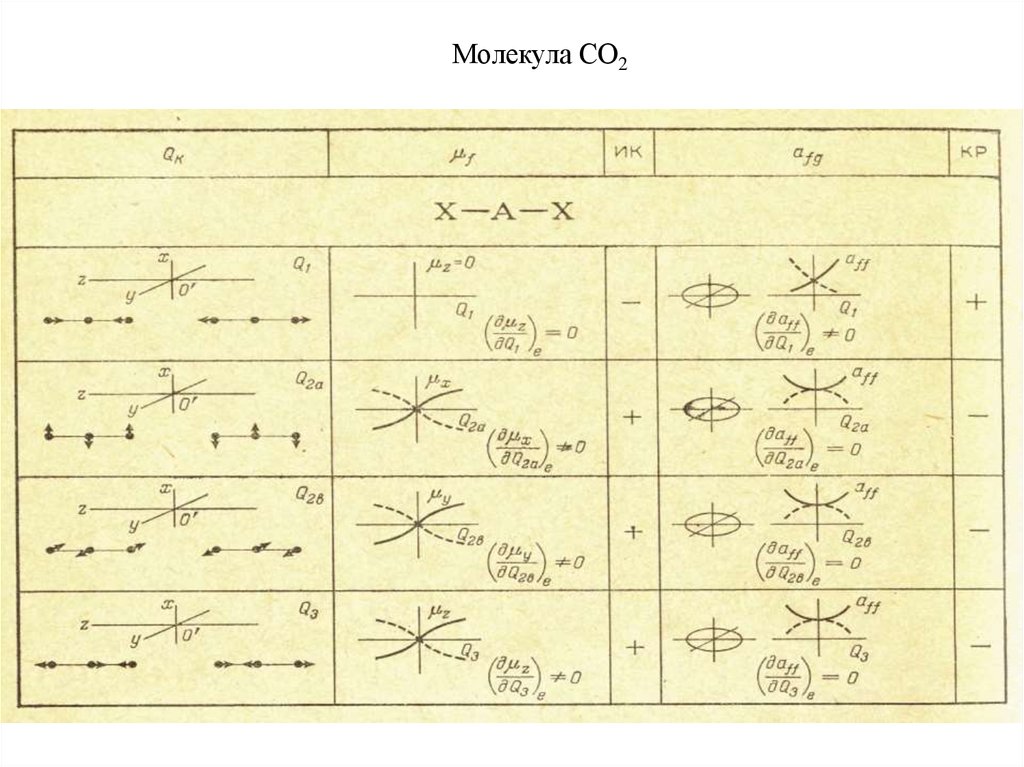
5. Молекула СО2
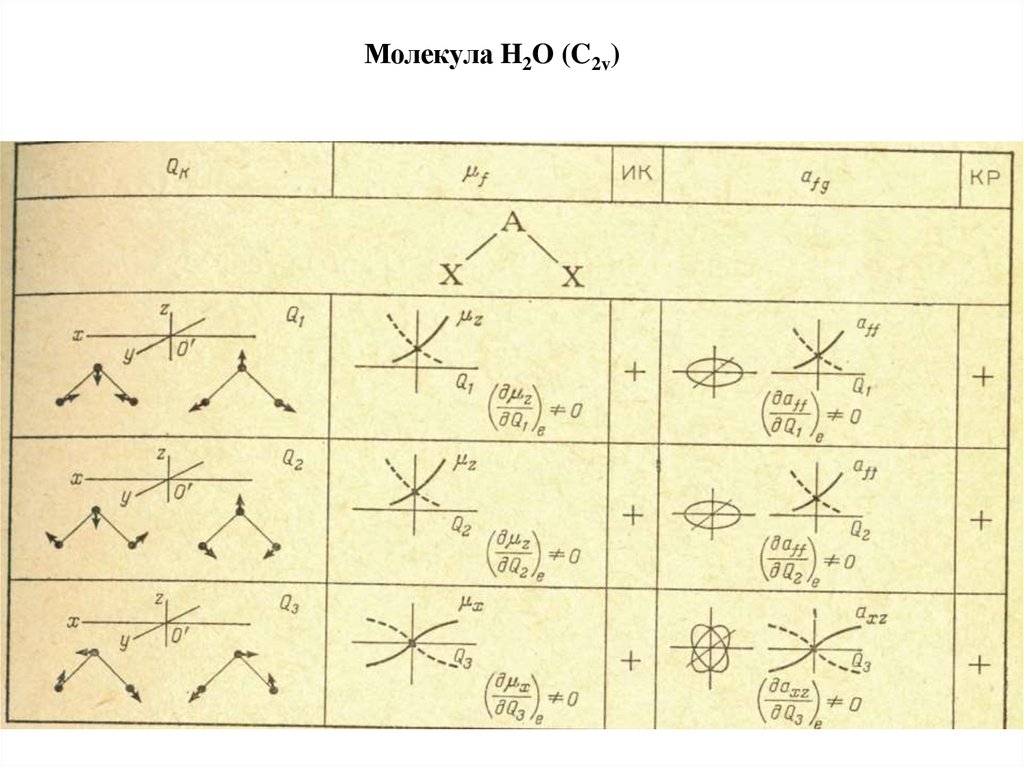
6. Молекула H2O (C2v)
7. Квантово–механическая теория
Общее собственное значение колебательной энергии:n
n
E[ v ] (v1 ...v n ) E k (v k ) hc
k 1
uk
1
k 1 2
n
1
w
(v k
) hc k (v k
)
tk
2
2
k 1
c
1
n
Волновая функция: y [v ] y k (Qk )
k 1
m
d
w
Если есть вырожденные колебания, то E[ v ] (v1 ...v n ) hc k (v k
)
2
k 1
m
m
d
d
В общем случае: E[ v ] (v1 ...v n ) hc[ w k (v k ) x kl (v k k )(vl l ) ...]
2 k ,l 1
2
2
k 1
d
8. Вращательная структура колебательных переходов
Правила отбора в общем случае:J 0 1
При || типе колебаний происходит изменение электрического дипольного
момента в направлении главной оси вращения, совпадающей с осью симметрии
высшего порядка.
При втором ( ) типе колебаний изменение компоненты дипольного
момента происходит в направлении, перпендикулярном оси a .
Это приводит к различию в правилах отбора и виду спектров.
Формула для Q –ветви ( J 0 ):
Q (J ) v 'v '' ( Bv ' Bv '' ) J ( Bv ' Bv '' ) J 2
9.
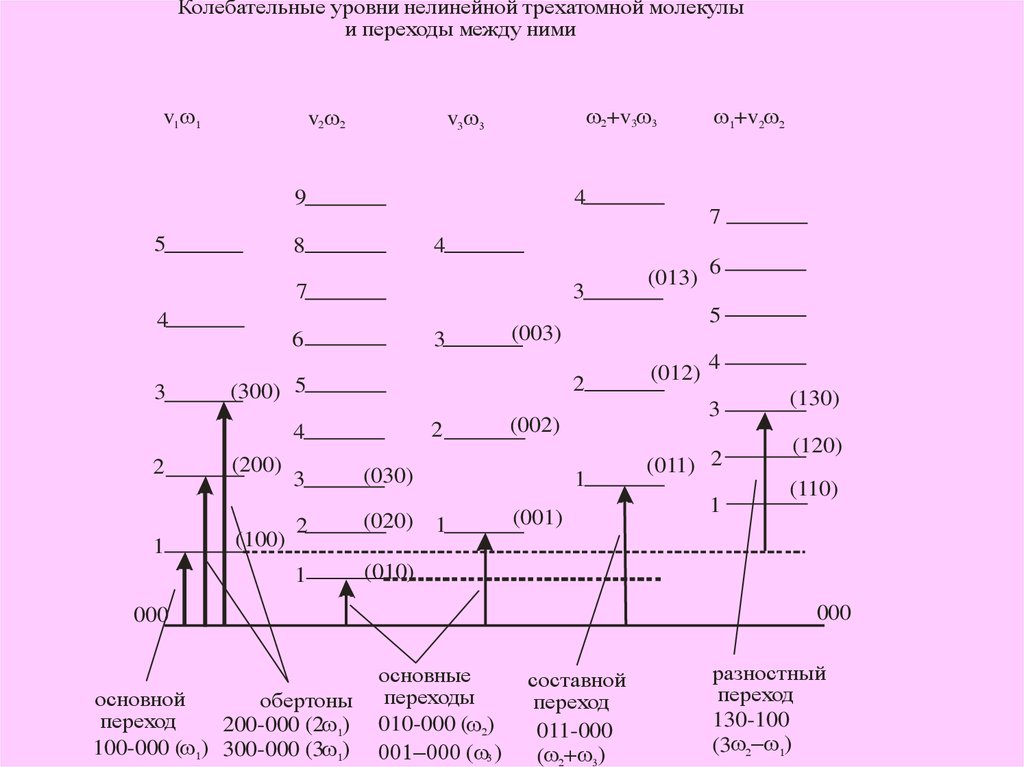
Колебательные уровни нелинейной трехатомной молекулыи переходы между ними
v1w1
v2w2
w2+v3w3
v3 w3
9
5
4
8
3
3
6
3
2
2
4
2
1
(100)
3
2
(020)
1
(010)
1
1
(001)
(011) 2
1
(130)
(120)
(110)
000
000
основной
обертоны
переход
200-000 (2w1)
100-000 (w1) 300-000 (3w1)
(012) 4
3
(002)
(030)
(013) 6
5
(003)
(300) 5
(200)
7
4
7
4
w1+v2w2
основные
переходы
010-000 (w2)
001 000 (w3 )
составной
переход
011-000
(w2 w3)
разностный
переход
130-100
(3w2 w1)
10. Правила отбора
Тип волчка, ккоторому
принадлежит
молекула
Линейный
волчок
Вид полосы
( Z )
( X , Y )
Правила отбора для
и K
J
J 1
J 0, 1
Число и
характер
ветвей
полосы
Две ветви
P, R
Три ветви
P , Q, R
Правила
отбора
Сферический
волчок
Симметричный
волчок
( X , Y , Z )
( Z )
( X , Y )
J 0, 1
Три ветви
P , Q, R
J 0, 1
K 0 (если К ' ' 0)
J 1
K 0 (если K ' ' 0)
J 0, 1
K 1
Три ветви
P , Q, R
Две ветви
P, R
Три ветви
P , Q, R
Асимметричный
волчок
X ( X )
Y ( Y )
Z ( Z )
J 0, 1
Три ветви
P , Q, R
11.
Характеристическиечастоты колебаний
для некоторых связей








 Физика
Физика








