Синтез логических выражений

Синтез логических
выражений
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 1.
Шаг 2. Для каждой из них
записать логическое
выражение, которое
истинно только для этой
строки.
Шаг 3. Сложить эти выражения
и упростить результат.
X A B A B A B
Дизъюнктивная нормальная
форма
(ДНФ)

3.

Совершенная Дизъюнктивная
Нормальная Форма (СДНФ)
Обладает свойствами:
включает различные элементарные конъюнкции;
все логические слагаемые формулы содержат все
переменные, которые входят в функцию F;
ни в одном логическом слагаемом не содержится
переменная и её отрицание.
К СДНФ возможно привести любую формулу
алгебры логики. Исключение составляет только
тождественно ложная формула.
Пример:
F X Y Y X X Y

4.

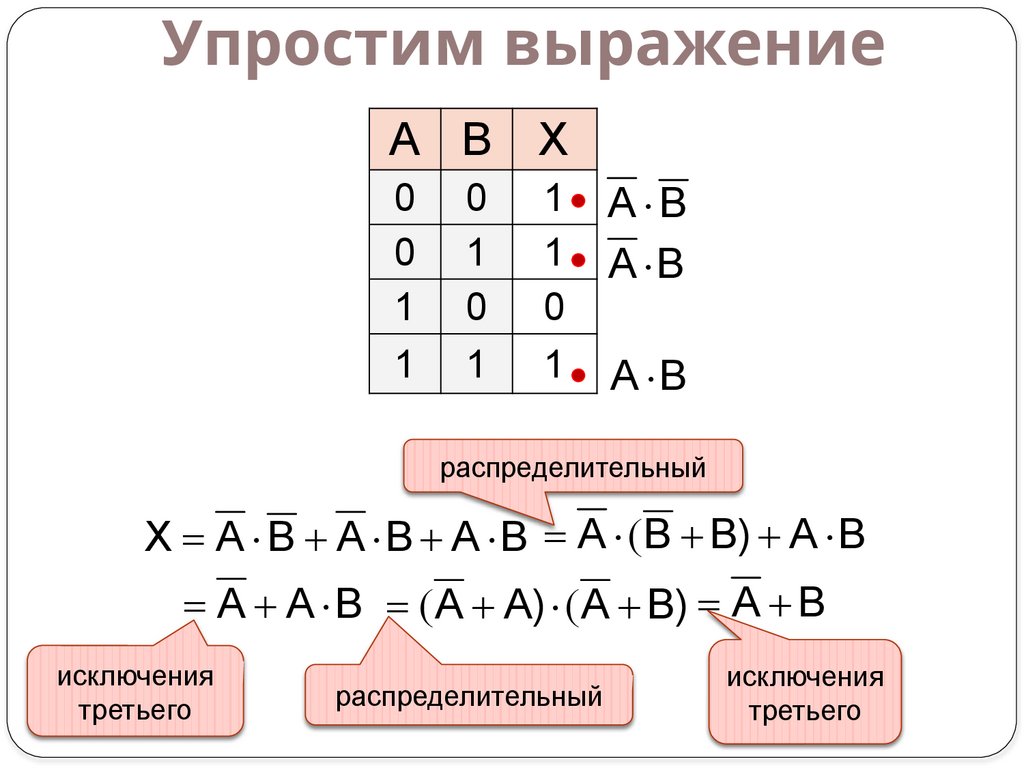
Упростим выражение
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
A B
A B
распределительный
X A B A B A B A (B B) A B
A A B ( A A) ( A B) A B
исключения
третьего
распределительный
исключения
третьего

5.

Синтез логических выражений (2
способ)
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое
истинно только для этой
строки.
Шаг 3. Сложить эти выражения
и упростить
результат,
X
который равен
.
Шаг 4. Сделать инверсию.
X A B X A B A B
? Когда удобнее применять 2-ой способ?

6.

Синтез логических выражений (3
способ)
A B
X
0
0
1
1
0
1
0
1
0
1
0
1
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое ложно
только для этой строки.
Шаг 3. Перемножить эти
выражения и упростить
результат.
X (A B) ( A B)
Конъюнктивная нормальная
форма
(КНФ)

7.

Совершенная Конъюнктивная
Нормальная Форма (СКНФ)
Обладает свойствами:
в ней отсутствуют одинаковые элементарные
дизъюнкции;
дизъюнкции не содержат одинаковые переменные;
все дизъюнкции содержат каждую переменную из
входящих в конъюнктивную нормальную функцию
такого типа.
К СКНФ возможно привести любую формулу
алгебры логики. Исключение составляет только
тождественно истинная формула.
Пример: F ( X Y ) ( X Y ) ( X Y )

8.

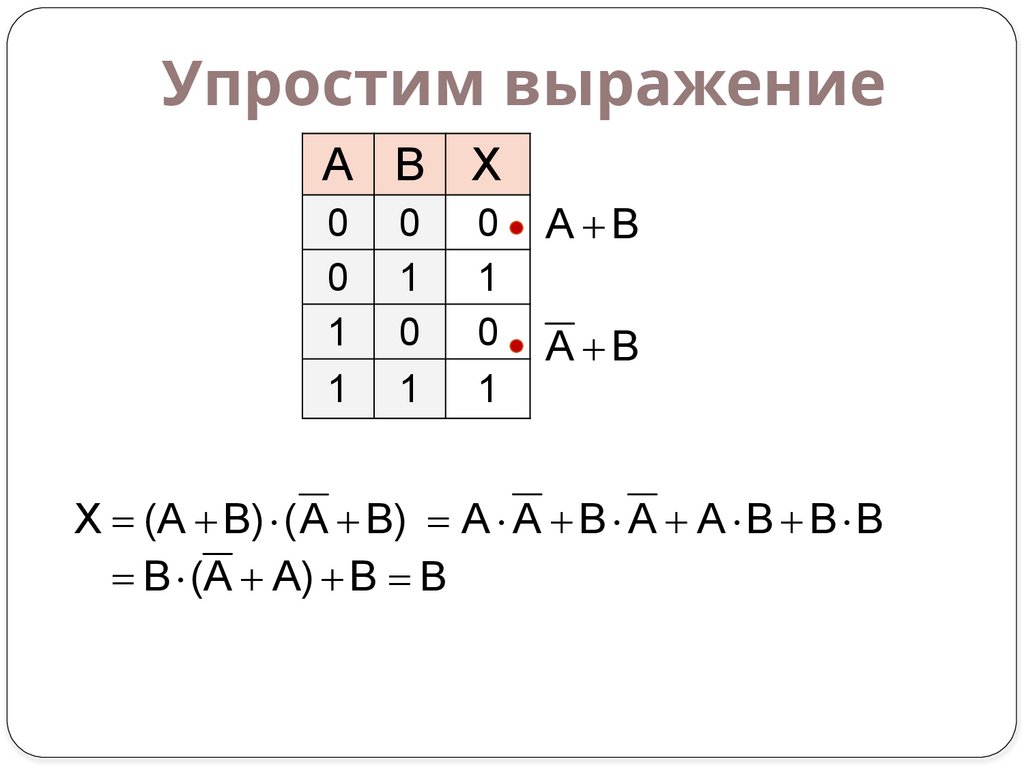
Упростим выражение
A B
X
0
0
1
1
0
1
0
1
0
1
0
1
A B
A B
X (A B) ( A B) A A B A A B B B
B (A A) B B

9.

Синтез логических
выражений
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
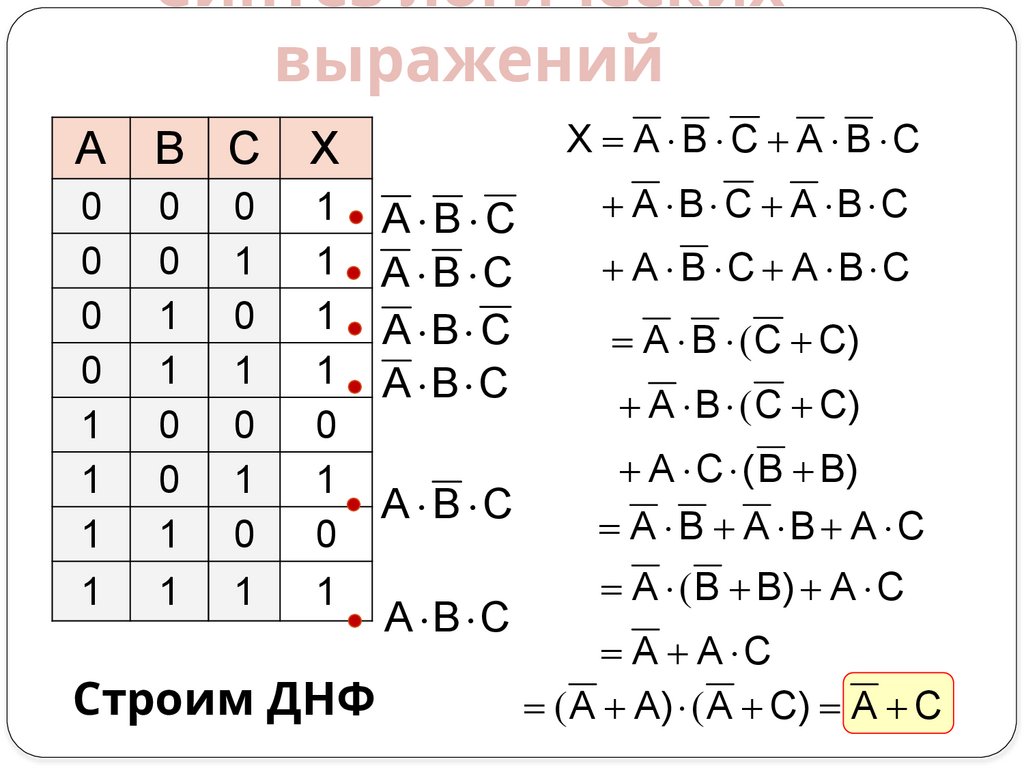
Строим ДНФ
X A B C A B C
A B C
A B C
A B C
A B C
A B C
A B C
A B C A B C
A B C A B C
A B ( C C)
A B ( C C)
A C ( B B)
A B A B A C
A (B B) A C
A A C
( A A) ( A C) A C

10.

Синтез логических выражений (2 способ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
X A B C A B C
A C ( B B)
A C
X A C A C
A B C
A B C

11.

Синтез логических выражений (3 способ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
Строим КНФ
X ( A B C) ( A B C)
( A C) B B
X A C
A B C
A B C

English Русский Правила