Функция полезности

1. Функция полезности

Аддитивная функция полезности:
U x p W x
n
a
i
j 1
j
j
i
Мультипликативная функция полезности:
U x W j xi
n
m
i
pj
j 1
n
где p j – вес j-го критерия, p j 1
j 1
W x – оценка полезности i-ой альтернативы
j
i
по j-ому критерию (единичная полезность)

2. Определение единичной полезности альтернативы

Первый подход (на основе идеального варианта с
эталонными характеристиками):
Для критерия на максимум:
y x
W x y
i
j
j
i
этал
Для критерия на минимум:
y
W x y
x
этал
j
i
j
i
где y j xi оценка i-ой альтернативы по j-му критерию;
y этал эталонное (максимальное или минимальное)
значение критерия

3. Определение единичной полезности альтернативы

Второй подход (на основе максимального и минимального
значений критериев по множеству рассматриваемых
альтернатив):
Для критерия на максимум:
y x y
W x y y
i
j
j
i
max
Для критерия на минимум:
min
min
y y x
W x y y
max
j
i
j
i
max
min
где y j xi оценка i-ой альтернативы по j-му критерию;
ymin , ymax минимальное и максимальное значения
критерия

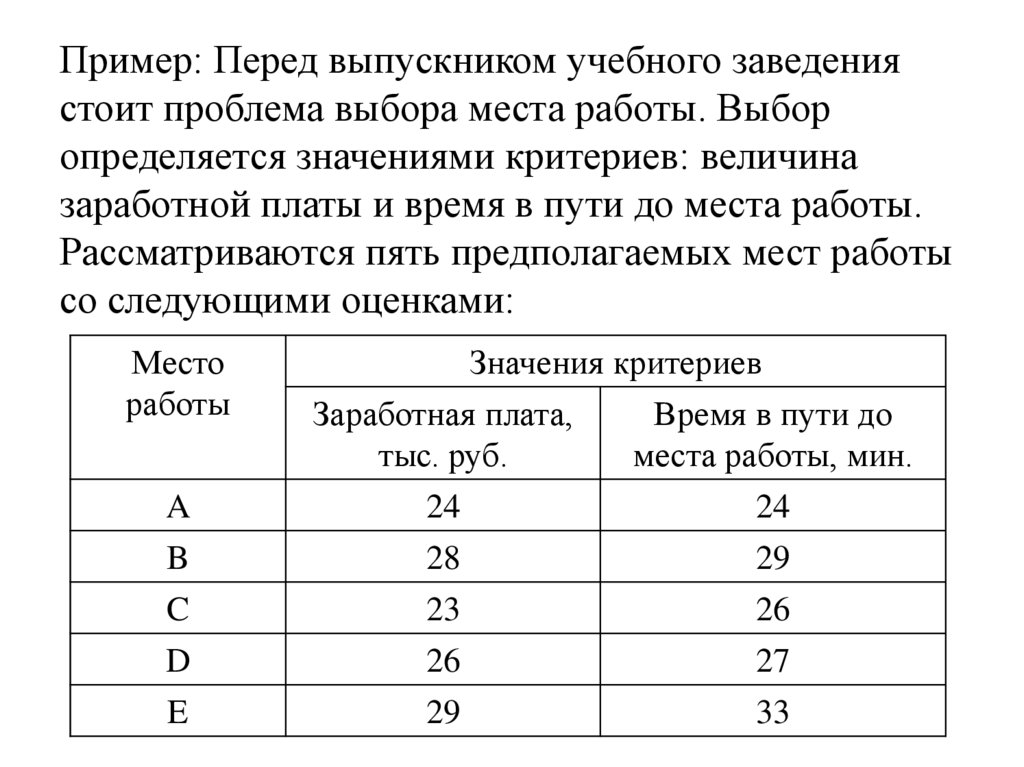
4. Пример: Перед выпускником учебного заведения стоит проблема выбора места работы. Выбор определяется значениями критериев:

величина
заработной платы и время в пути до места работы.
Рассматриваются пять предполагаемых мест работы
со следующими оценками:
Место
работы
A
B
C
D
E
Значения критериев
Заработная плата,
Время в пути до
тыс. руб.
места работы, мин.
24
24
28
29
23
26
26
29
27
33

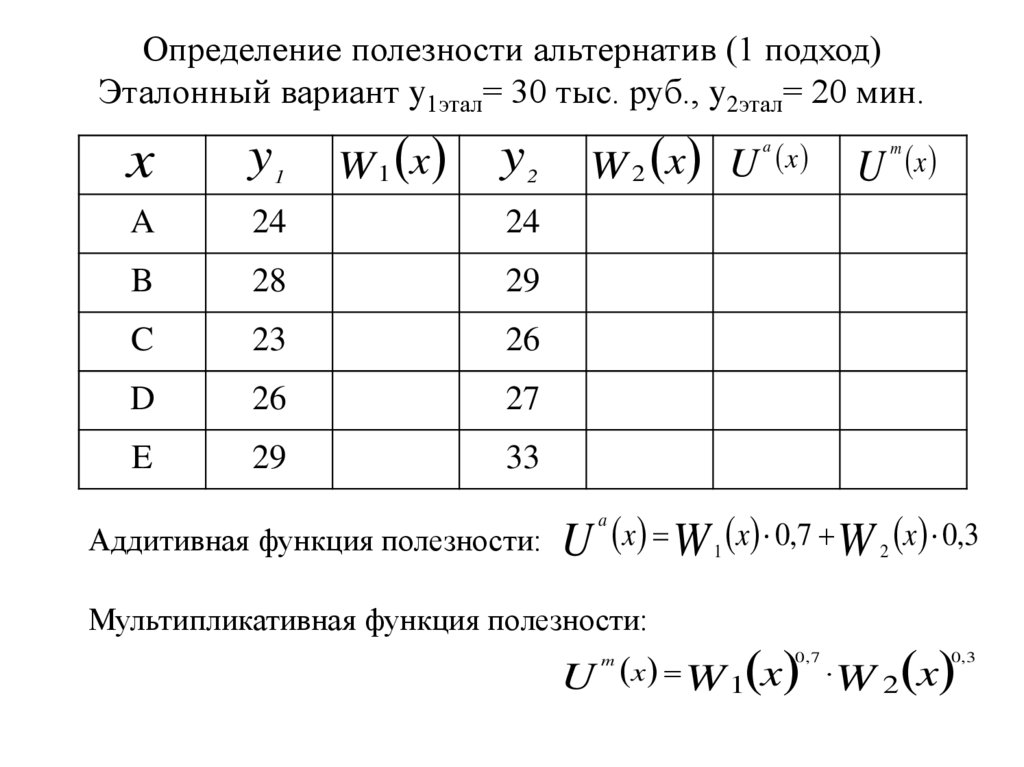
5. Определение полезности альтернатив (1 подход) Эталонный вариант y1этал= 30 тыс. руб., y2этал= 20 мин.

W 1 x
x
y
A
24
24
B
28
29
C
23
26
D
26
27
E
29
33
1
y
W 2 x U x U x
a
2
m
Аддитивная функция полезности: U x W 1 x 0,7 W 2 x 0,3
a
Мультипликативная функция полезности:
U x W 1 x
m
0, 7
W 2 x
0,3

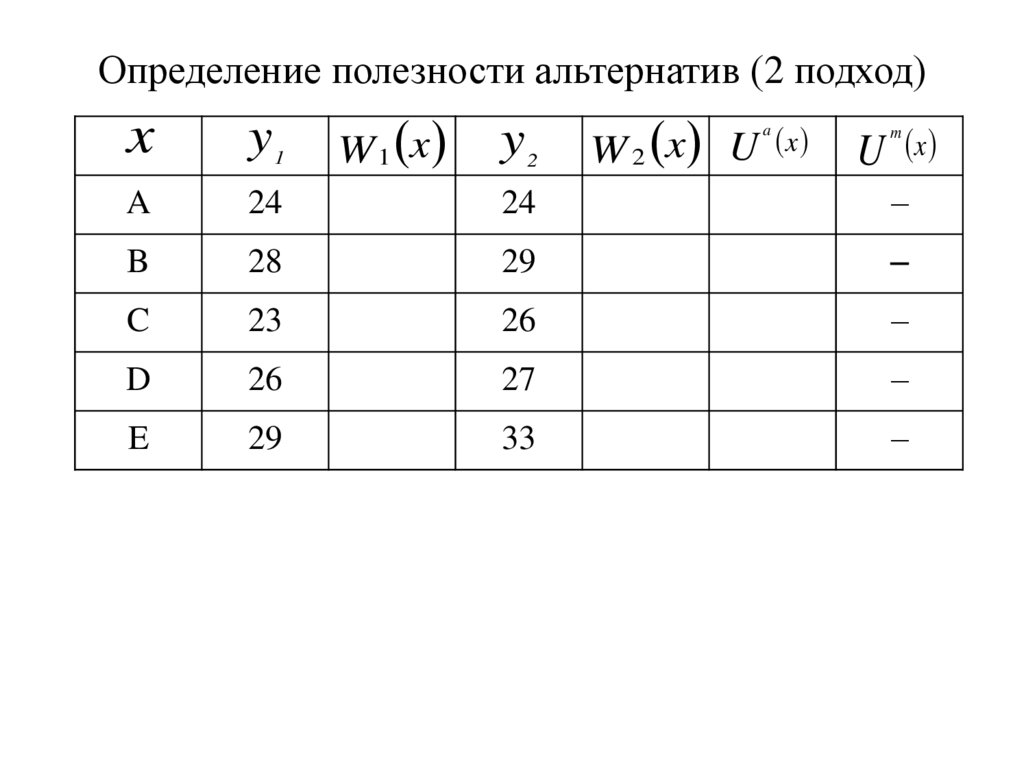
6. Определение полезности альтернатив (2 подход)

W 1 x
W 2 x U x U x
x
y
A
24
24
B
28
29
C
23
26
D
26
27
E
29
33
1
y
a
2
m