Похожие презентации:
Аппроксимация функции
1. АППРОКСИМАЦИЯ ФУНКЦИИ
2. Постановка задачи
1. Простейшая задача: в дискретные моментывремени
t1 , t2 ,...,tn ,...
наблюдаются значения
функции f ti , i 1, n ; требуется восстановить её
значения при других t .
16.08.2018
.
2
3.
2. Для функцииf x
известно её аналитическое
представление, но вычисление каждого значения
сопряжено с большим объёмом вычислений.
Например,
2 700
2
f x cos sin x cos kx , a x b
k
1
16.08.2018
3
4.
3. Функция задаётся своими значениями в узлахxi , i 1, n , из интервала a x b .
В вычислительном процессе используется эта
таблица.
16.08.2018
4
5.
4. Задача численного решенияопределённого
интеграла или дифференциального уравнения.
16.08.2018
5
6.
Области использования аппроксимации :моделирование;
планирование и статистическая обработка
данных;
определение значений функции при аргументах
отсутствующих в таблице;
табулирование функции;
представление сложной функции более простой в
определённых границах значений её аргументов;
во всех других случаях, где нужно выполнить
приближение одних функций другими, более
простыми, с допустимой для практики точностью.
16.08.2018
6
7.
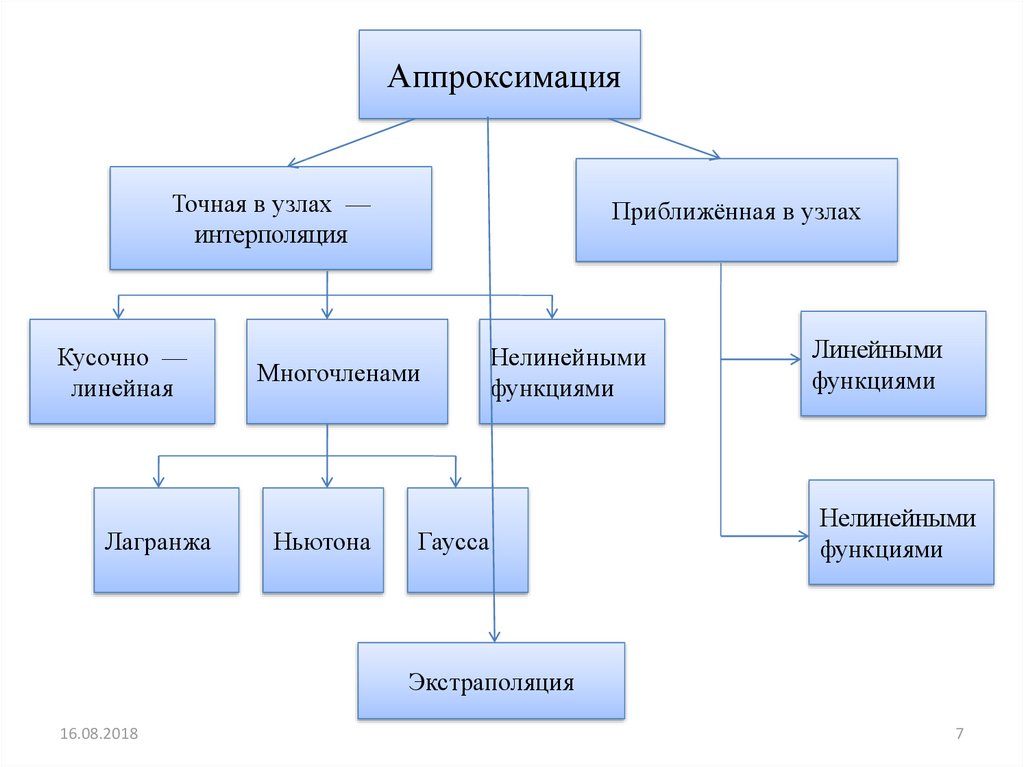
АппроксимацияТочная в узлах —
интерполяция
Кусочно —
линейная
Лагранжа
Приближённая в узлах
Многочленами
Ньютона
Нелинейными
функциями
Гаусса
Линейными
функциями
Нелинейными
функциями
Экстраполяция
16.08.2018
7
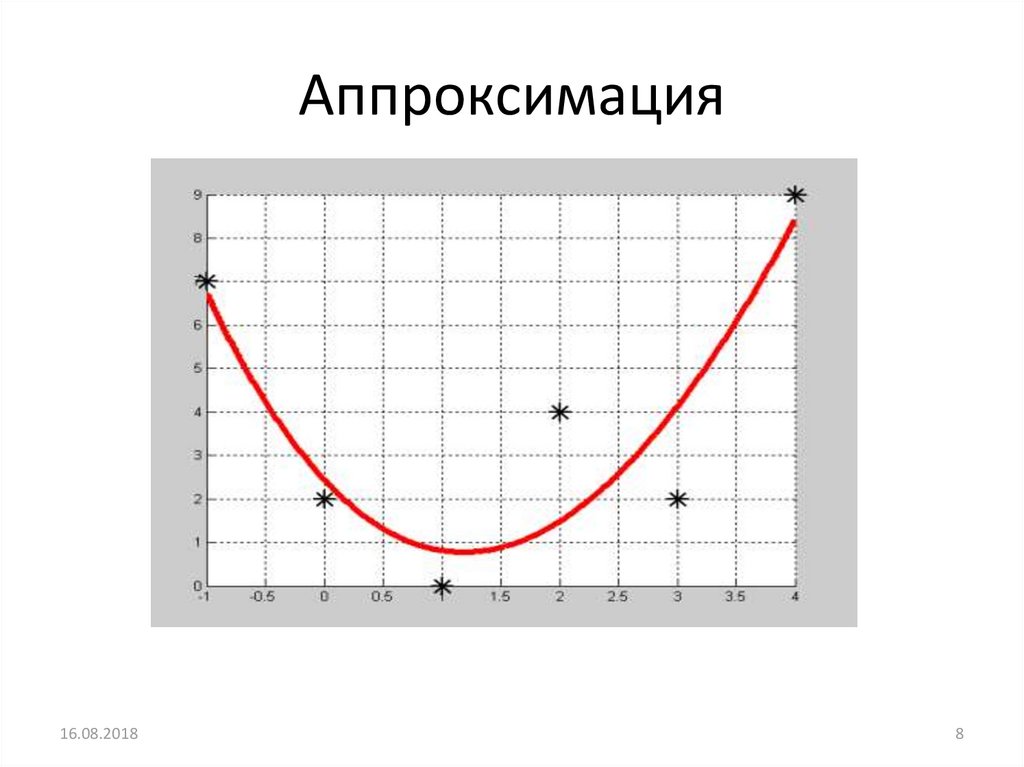
8. Аппроксимация
16.08.20188
9.
Если аппроксимация функции происходит впромежуточных узлах, т.е.
g xi f xi тогда
a x b
говорят
о
, причём
точной
интерполяции.
Интер – между.
16.08.2018
9
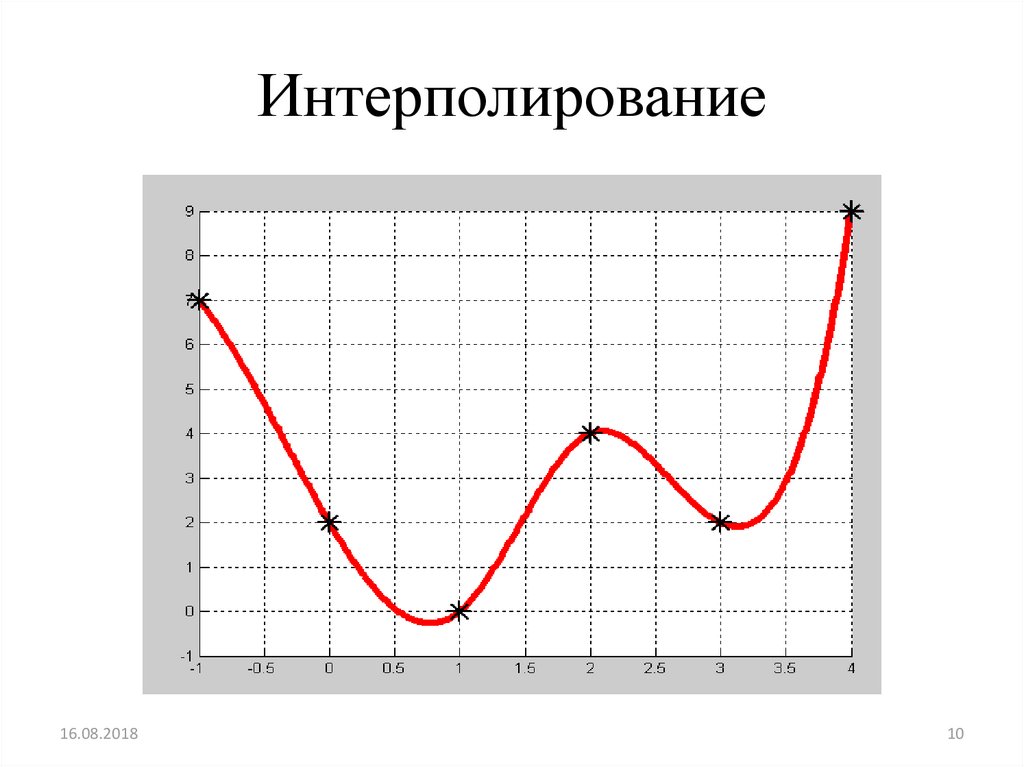
10. Интерполирование
16.08.201810
11.
Если аппроксимацияфункции происходит вне
рассматриваемого отрезка
~
x x0 , xn
, тогда
говорят об экстраполяции.
экстра – вне.
16.08.2018
11
12. ИНТЕРПОЛИРОВАНИЕ
Основные понятия.Задано множество точек x0 , x1 ,..., xn , принадлежащих
отрезку
a, b
и значения функции
f x0 , f x1 , ..., f xn
в этих точках.
Требуется найти функцию
этом отрезке такую, что
y x , определённую на
xi f xi
в указанных
точках
16.08.2018
12
13.
ОБОБЩЁННЫЙ ПОЛИНОМn
x C0 0 x C1 1 x ... Cn n x Ci i x
i 0
– числовые коэффициенты,
Ci
i x
n
0
– множество функций, определённых на
рассматриваемом отрезке и линейно независимых
на нём.
Такие функции называются БАЗИСНЫМИ.
16.08.2018
13
14.
1. Последовательность степенейx .
i
2. Последовательность тригонометрических
функций
cos ti x, sin ti x .
3. Последовательность экспонент
e .
i x
4. Последовательность дробно-рациональных
Pi x
функций
.
Qi x
16.08.2018
14
15.
Многочлен Тейлора m-ой степени:m
Tm x
f
k 0
Для
x0 0
k
x0 x x k
0
k!
можно использовать известные
разложения функций.
16.08.2018
15
16.
Погрешность метода — остаточный член формулыТейлора в форме Лагранжа:
c
m 1
x x0
Rm x
m 1 !
f
m 1
где c лежит между x и x0.
Если c
не принадлежит интервалу сходимости
ряда Тейлора, то погрешность не уменьшается.
16.08.2018
16
17. Существование и единственность интерполяционного многочлена
Теорема.Для таблично заданной функции f x на множестве
узлов xi , i 0, n существует единственный
интерполяционный многочлен степени
m n ,
удовлетворяющий условию Lm xi f xi , i 0, n.
Доказательство:
16.08.2018
17
18.
mБудем искать многочлен Lm x ak x
k
k 0
Нужно найти коэффициенты a0, a1, ..., an.
Они должны удовлетворять СЛУ
a0 a1 x0 a x ... a x f ( x0 ),
2
m
a0 a1 x1 a2 x1 ... am x1 f ( x1 ),
................................................
a a x a x 2 ... a x m f ( x ).
2 n
m n
n
0 1 n
2
2 0
m
m 0
В системе (m+1) неизвестных, (n+1) уравнение.
16.08.2018
18
19.
Если система крамеровская, то решениеСУЩЕСТВУЕТ и ЕДИНСТВЕННОЕ.
Пусть m+1 = n+1, т.е. m = n. Главный определитель
системы
1 x0 x02
1 x1 x12
1 xn xn2
x0n
x1n
— определитель Вандермонда.
xnn
( xi x j )
0 i j n
Если все узлы различны, то 0 .
Теорема доказана.
16.08.2018
19
20.
Метод нахождения коэффициентов,используемый при доказательстве теоремы,
называется
методом неопределённых коэффициентов.
16.08.2018
20
21.
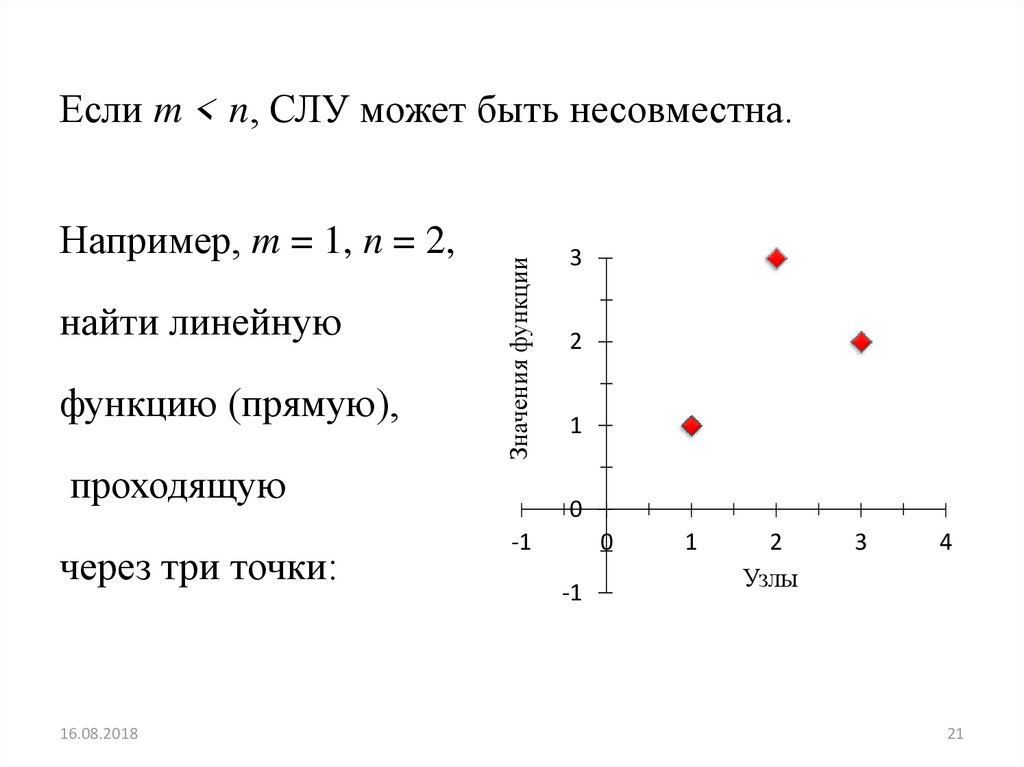
Например, m = 1, n = 2,найти линейную
функцию (прямую),
Значения функции
Если m < n, СЛУ может быть несовместна.
проходящую
через три точки:
16.08.2018
3
2
1
0
-1
0
-1
1
2
Узлы
3
4
21
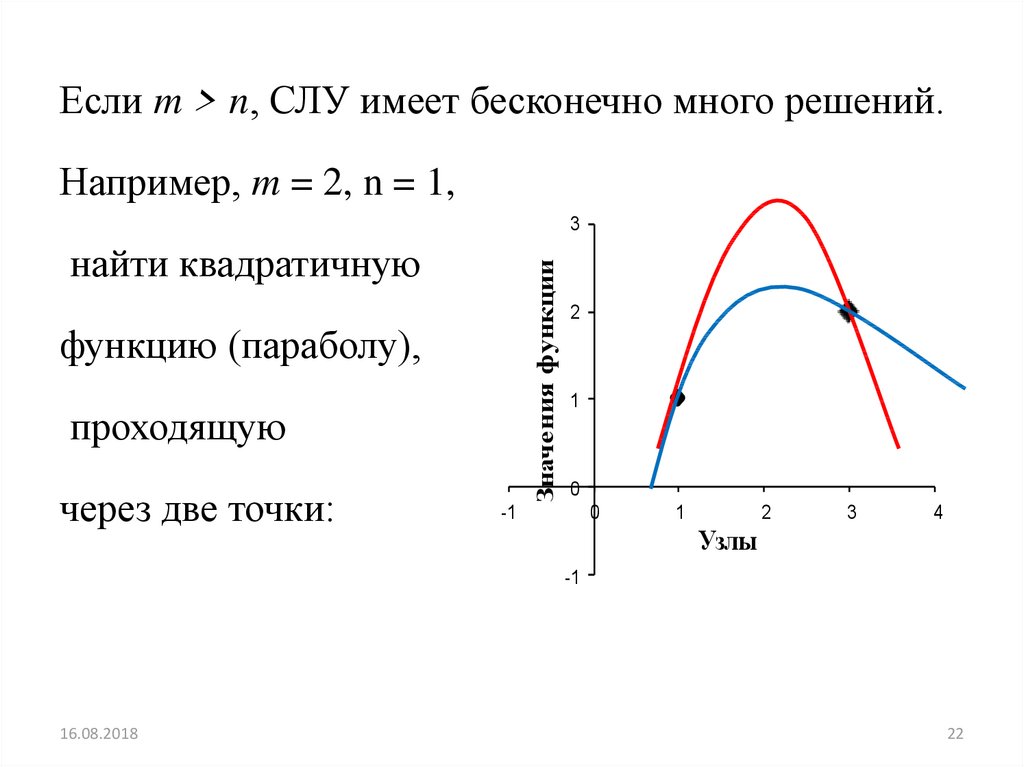
22.
Если m > n, СЛУ имеет бесконечно много решений.Например, m = 2, n = 1,
найти квадратичную
функцию (параболу),
проходящую
через две точки:
-1
Значения функции
3
2
1
0
0
1
2
3
4
Узлы
-1
16.08.2018
22
23. Интерполяционный многочлен Лагранжа
Выразим многочлен Ln(x) как линейнуюкомбинацию значений f0, f1, ..., fn:
Ln ( x) 0 ( x) f 0 1 ( x) f1 n ( x) f n
16.08.2018
23
24.
Рассмотрим в качестве подсказки частные случаи.1) n = 1:
x0, x1 — узлы, f0, f1 — значения в узлах
Найти 0 ( x) f 0 1 ( x) f1 f ( x)
при x0
f 0 1 f 0 0 f1
0 ( x0 ) 1, 1 ( x0 ) 0
при x1
f1 0 f 0 1 f1
0 ( x1 ) 0, 1 ( x1 ) 1
1
0 ( x) ( x x1 )
x 0 x1
16.08.2018
и
1
1 ( x) ( x x0 )
x1 x0
24
25.
2) n=2:Найти
x0, x1, x2 — узлы, f0, f1 , f2— значения в узлах
0 ( x) f 0 1 ( x) f1 2 ( x) f 2 f ( x)
при x0 f 0 1 f 0 0 f1 0 f 2
при x1 f1 0 f 0 1 f1 0 f 2
0 ( x1 ) 0, 1 ( x1 ) 1, 2 ( x1 ) 0
при x3 f 2 0 f 0 0 f1 1 f 2
( x x1 ) ( x x2 )
0 ( x)
;
x0 x1 x0 x2
0 ( x0 ) 1, 1 ( x0 ) 0, 2 ( x0 ) 0
0 ( x2 ) 0, 1 ( x2 ) 0, 2 ( x2 ) 1
( x x0 ) ( x x2 )
1 ( x)
;
x1 x0 x1 x2
( x x0 ) ( x x1 )
2 ( x)
x 2 x0 x2 x1
16.08.2018
25
26.
Опр. Интерполяционным многочленом Лагранжаn
называется полином
Ln ( x ) i ( x ) f i
i 0
.
Опр. Лагранжевы коэффициенты — i ( x)
для каждого i = 0, ..., n.
(x x j )
(x
0 j n
j i
i
xj)
Замечание:
Лагранжевы коэффициенты удовлетворяют тождеству
n
i 0
16.08.2018
i
( x ) 1 , т.к. обладают свойством:
1, i j
i ( x j )
0, i j
26
27.
Пример 1.Построить интерполяционный полином Лагранжа для
функции, заданной таблицей
xi
-1
2
3
5
f xi
-1
3
2
4
Так как задано 4 узла интерполяции, то степень полинома не
выше третьей.
x 2 x 3 x 5
x 1 x 3 x 5
L3 x 1
3
1 2 1 3 1 5
2 1 2 3 2 5
16.08.2018
27
28.
x 1 x 2 x 5x 1 x 2 x 3
2
4
.
3 1 3 2 3 5
5 1 5 2 5 3
Можно вычислить приближённое f x значение в
точке ~
x 2.5.
f 2.5 L3 2.5 2.4635
16.08.2018
28
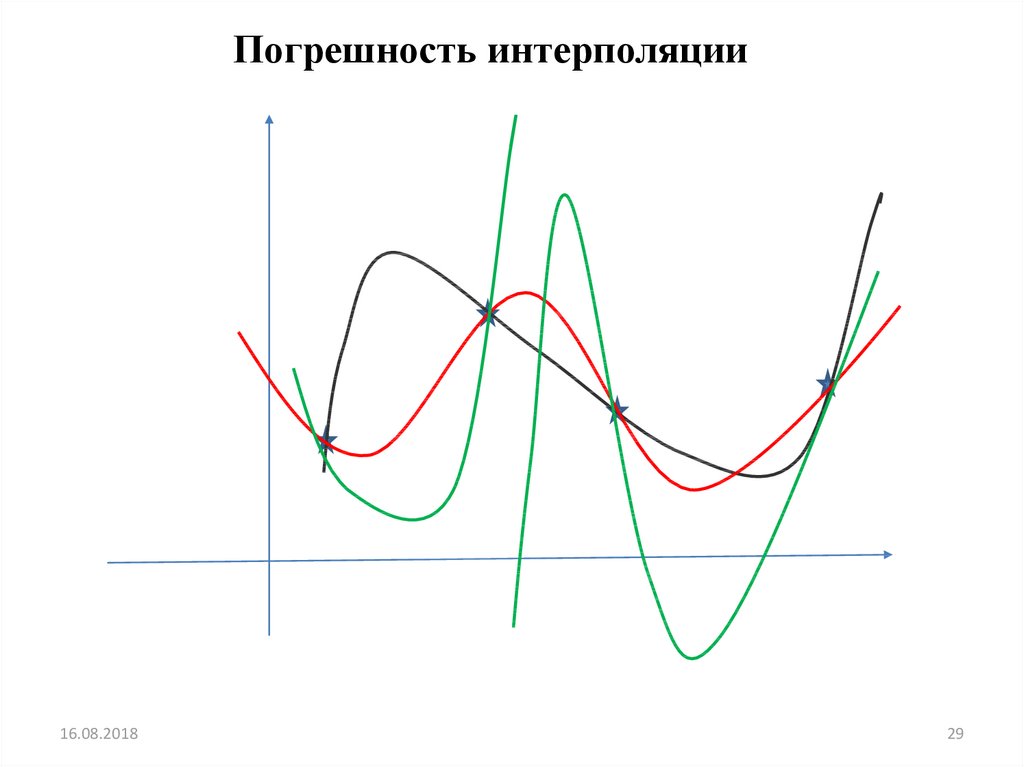
29.
Погрешность интерполяции16.08.2018
29
30.
Погрешность интерполяционного многочленаЛагранжа
Предполагаем, что
f ( x) C n 1 a, b .
Ln(x) — многочлен Лагранжа: Ln ( xi ) f ( xi ) для всех i=0,...,n
[a,b] — отрезок, содержащий узлы x0, x1, ..., xn.
Найдем оценку отличия значения f (x) от значения Ln(x) в
точке
~
x a, b , не совпадающей ни с одним из узлов,
иначе, величину остаточного члена
Rn ( ~
x ) f (~
x ) Ln ( ~
x)
16.08.2018
30
31.
Запишем равенствоf ( x) Ln ( x) R( x) Ln ( x) n 1 ( x) С
где
n 1 ( x) ( x x0 ) ( x xn ) – многочлен
определённый через узлы x0, x1, ..., xn
С – некоторая постоянная (параметр).
Подберём параметр С так, чтобы f (x) обращалась в
нуль в точке , для которой делаем оценку, т.е. ~x a, b и
~
x xi , i 0, n .
К функции f (x) на каждом из отрезков
xi , xi 1 ,
i 0, n
применима теорема Ролля
16.08.2018
31
32.
Введём в рассмотрение функцию(t ) Ln (t ) n 1 (t ) C f (t )
R( x)
(t ) 0
если t x0 , x1 ,..., xn , ~
x
всего (n+2) точки
(t ) 0
(n+1) точка на [a,b]
(t ) 0
n точек на [a,b]
...
( n 1) (t ) 0
16.08.2018
1 точка на [a,b]
по т. Ролля, если
функция в двух
точках равна 0,
то между этими
точками
существует
точка, в которой
производная
обращается в 0
32
33.
Итак, существует a, b :Тогда
( n 1)
n 1
( n 1) ( ) 0 .
0
( x) Ln ( x) n n 11 ( x) C f ( n 1) ( x)
и n ( n 1) ( x) (n 1) ! , т. к.
n 1 ( x) ( x x0 ) ( x xn )
получаем (n 1)! С f ( n 1) ( ) 0
Отсюда
16.08.2018
f ( n 1) ( )
С
(n 1)!
33
34.
f ( x) Ln ( x) Rn ( x) f ( x) Ln ( x) n 1 ( x) Cn 1
( )
f ( x) Ln ( x) n 1 ( x)
n 1 !
f
Для остаточного члена получаем выражение
f ( n 1) ( )
Rn ( x) n 1 ( x)
(n 1)!
16.08.2018
34
35.
Точное представлениеf (x) через её
интерполяционный многочлен Лагранжа Ln (x) :
f ( n 1) ( )
f ( x) Ln ( x) n 1 ( x)
(n 1)!
где a, b и зависит от x.
Можно оценить предельную абсолютную
погрешность интерполирования на отрезке a, b с
помощью формулы
max R( x) max n 1 ( x)
a ,b
16.08.2018
a ,b
max f ( n 1) ( x)
a ,b
(n 1)!
35
36.
Пример 2.Оценить с какой точностью можно вычислить по
формуле Лагранжа ln 100.5, если известны значения
ln 100, ln 101, ln 102, ln 103 .
f x ln x, n 3, a x0 100, xn b 103,
f
4
6
x 4 ,
x
max
a, b
f
4
6
x 4
100
6
9
ln 100.5 L 100.5
0
.5
0
.5
1
.5
2
.5 2.344 10
4
100 4!
4 x
16.08.2018
36



















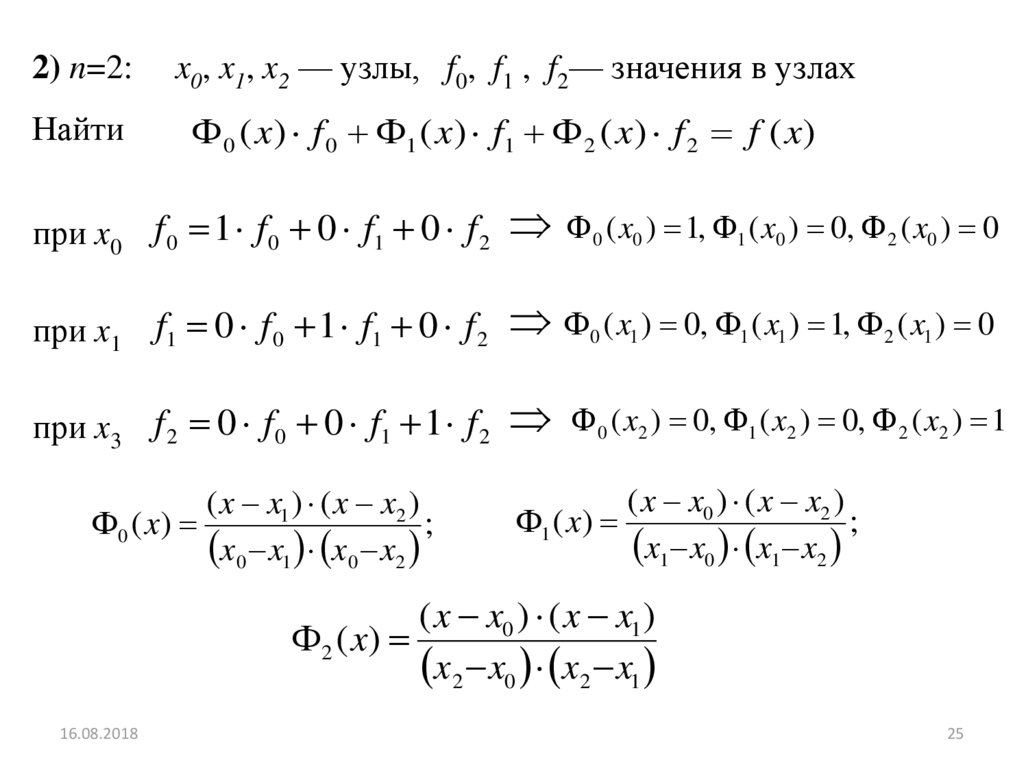










 Математика
Математика








