Применение PINN для решения уравнения Бесселя

1. Государственное бюджетное общеобразовательное учреждение города Москвы «Школа № 2117»

Применение PINN для
решения уравнения
Бесселя
Участники:
Ученики 10 «А» класса ГБОУ Школа №2117
Колганова Мария Ивановна, Командин
Артём Романович, Мищенко Александр
Сергеевич
Руководитель:
педагог ГБОУ Школа № 2117
Иванов Ярослав Анатольевич
Инженер НИЯУ МИФИ Ладыгин Станислав

2. Цель

Введени
е
Цель
Гипотеза
Исследовать влияние выбора функций активации (
Sigmoid, Tanh, Softplus, Sin)на точность и эффективность
нахождения функций Бесселя с помощью физически
информированных нейронных сетей (PINN).
Физически информированные нейронные сети (PINN)
демонстрируют высокую эффективность в решении уравнения
Бесселя, достигая точности, сравнимой с традиционными
численными методами. Это возможно при условии оптимального
подбора архитектуры сети, функции потерь и стратегии учёта
граничных условий.

3. Задачи

Задач
и
1.Изучение свойств и применений функций Бесселя
2.Изучение основ нейросетей в контексте PINN
3.Изучить алгоритм обучения PINN для решения
дифференциальных уравнений.
4.Разработать самообучающуюся нейросеть на основе физически
информированных нейронных сетей
(PINN) для решения уравнения Бесселя

4. Актуальность работы

Актуальность работы связана с развитием
физически информированных нейронных сетей
(PINN) как инструмента для численного
моделирования в физике и технике. Проект
направлен на тестирование PINN для решения
уравнения Бесселя, с фокусом на исследование их
эффективности при работе с уравнениями,
содержащими особенности и нелинейности.

5.

Свойства и
применения функций
Бесселя.
Функция Бесселя имеет следующий
вид:
Функции Бесселя широко применяются для
решения множества задач в различных областях
математической физики, а также для ответа на
актуальные технические вопросы
Наиболее распространенными
являются функции Бесселя первого и
второго рода.

6.

Основы
нейросетей в
контексте PINN
Физически информированные
нейронные сети (PINN) — это
подход в машинном обучении,
объединяющий нейронные сети с
физическими законами,
описывающими поведение системы.
Идея очень проста: добавить известные
дифференциальные уравнения
непосредственно в функцию потерь при
обучении нейронной сети.

7.

Функция потерь и ее
роль в обучении.
В сфере ИИ и МЛО функция потерь
является важнейшим компонентом
обучающих моделей.
Функция потерь измеряет расхождение между
предсказанными значениями модели и фактическими
данными. Чем выше значение потерь, тем хуже
производительность модели, а чем ниже — тем лучше
её результаты.

8.

Обучение без
учителя
Основная цель обучения без учителя —
группировок в данных и обнаружение скрытых
паттернов.
Обучение без учителя — это метод
машинного обучения, при котором система
самостоятельно обучается решать задачу
без прямого вмешательства или контроля со
стороны человека.

9.

Алгоритм обучения PINN для решения
дифференциальных уравнений.
1 Интервал решения :
Определить интервал изменения
независимой переменной x
2 Архитектура нейронной
сети:
Выбор архитектуры
Функция активации
Входные данные
3 Процесс обучения:
Генерация обучающих данных : Генерация
обучающих данных: создание набора точек внутри
интервала x, для которых вычисляются значения
функции потерь, включающей в себя уравнение
Бесселя.
Выходные данные

10.

Результаты работы и их проверка (испытания,
апробация)
В итоге разработана
программа на языке Python.
Программа состоит из несколько
файлов:
‘main.py’
‘pinn.py’
‘trainer.py’
‘loss.py’
‘activation_factory.py’
‘config.json’

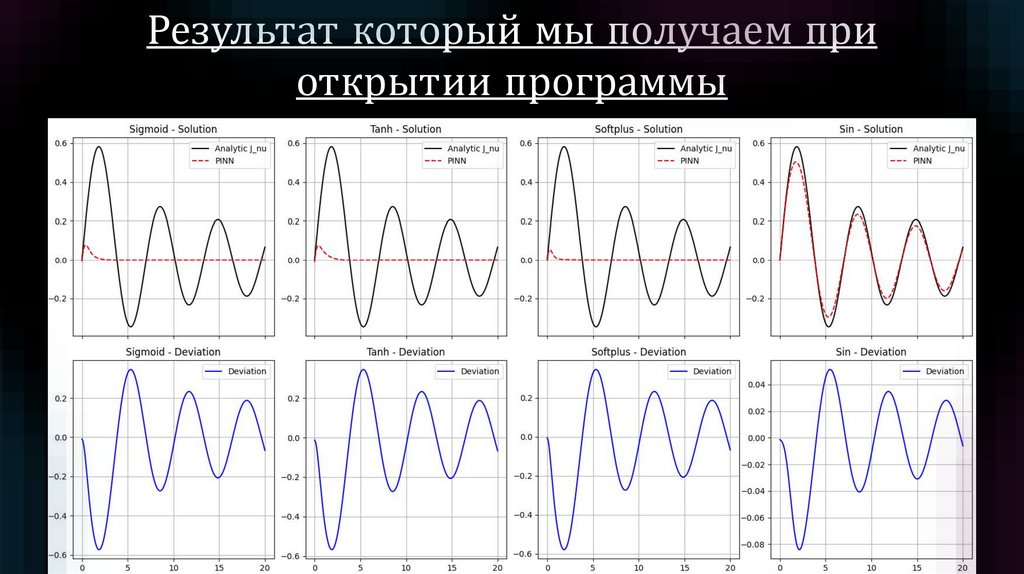
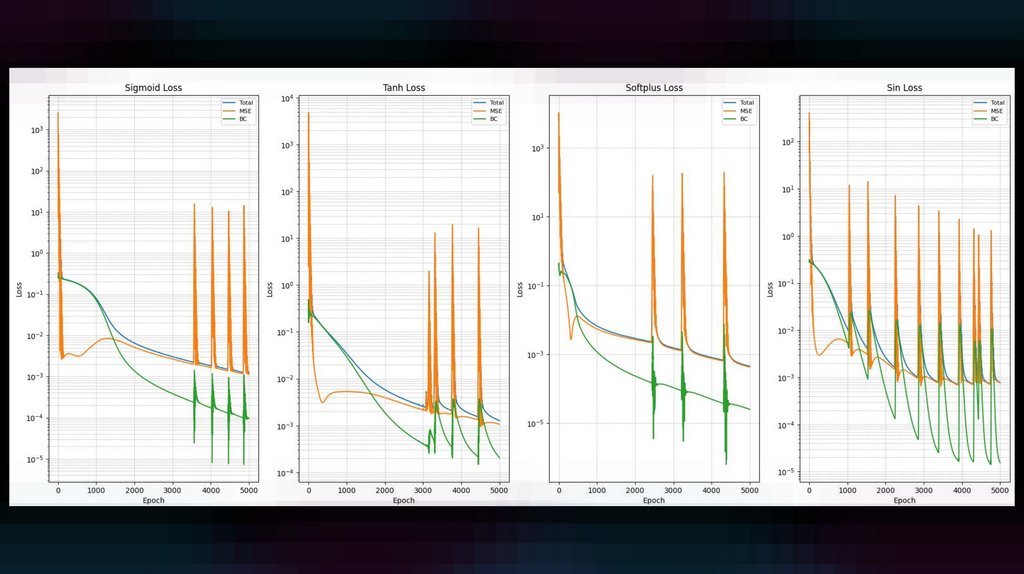
11.

Результат который мы получаем при
открытии программы

12.

13.

Вывод
1. Разработанная модель, основанная на методах PINN, демонстрирует
высокую точность в решении уравнения Бесселя, что подтверждается
её сопоставлением с аналитическими и численными решениями.
2. PINN гибок и устойчив, подходит для задач, где традиционные методы
менее эффективны.
3. Метод PINN интегрирует физические законы в обучение нейронной
сети, обеспечивая более точные и осмысленные результаты.

14.

Перспективы дальнейшей
работы
Оптимизация модели
Изучение потенциала ускорения процесса
обучения и улучшения точности модели
через оптимизацию архитектуры
нейронной сети и подбор оптимальных
гиперпараметров.
Расширение области применения
Адаптация модели для применения в
решении различных классов
дифференциальных уравнений.
Интеграция с реальными данными
Использование модели для решения прикладных
задач в физике, инженерии и других научных
областях, где необходимо нахождение решений
уравнения Бесселя.

15. Литература:

• Ватсон Г. . Теория бесселевых функций. — М.: ИЛ, 1949.
• Лагарис, I. Э., Ликас, А., и Фотиадис, Д. Я. (1998). Искусственные нейронные сети для решения обычных
и дифференциальных уравнений в частных производных. Транзакции IEEE по нейронным сетям.
• Зубов В. И. Функции Бесселя. Учебно-методическое пособие //М.: МФТИ. —2007.

16.

СПАСИБО
ЗА
ВНИМАНИ
Е