Полиномиальное и обратное полиномиальное хеширование. Лабораторная работа № 5

1.

Лабораторная
работа №5
ассистент кафедры ИТиСУ
Павлов Марк Владимирович
pavlov.mark@urfu.ru

2.

Общие вводные
В данной работе мы:
- применим полиномиальное и обратное полиномиальное хеширование
- разработаем свою хеш-таблицу
- применим ее для решения задачи
2

3.

Задача 1. Подстроки
Входной файл состоит из одной строки I, содержащей малые буквы английского алфавита.
Назовем подстроковой длиной L с началом S множество непрерывно следующих символов
строки.
Например, abcab содержит подстроки:
длины 1: a, b, c, a, b
длины 2: ab, bc, ca, ab
длины 3: abc, bca, cab
длины 4: abca, bcab
длины 5: abcab
В строках длины 1 есть два повторяющихся элемента — a и b. Назовем весом подстрок длины
L произведение максимального количества повторяющихся подстрок этой длины на длину L.
В нашем случае вес длины 1 есть 2 (2*1), длины 2 есть 4 (2*2), длины 3 — 3 (1*3), длины 4
— 4 и длины 5 — 5.
Требуется найти наибольший из всех весов различных длин.
3

4.

Задача 1. Подстроки
Стандартный ввод
Стандартный вывод
aabaabaabaabaa
24
abcab
5
4

5.

Задача 1. Подстроки
Полиномиальное хеширование (источник)
Если посчитать хеши для всех прификсов строки, то получение хеша любой подстроки будет занимать
константное время
5

6.

Задача 1. Подстроки
Полиномиальное хеширование (источник)
1. Определить некоторое большое простое: mod = 10**18 + 3
2. Определить некоторое простое, превышающее размер алфавита: p = 29
3. Завести массив для хранения хешей, а также отдельный массив для хранения степеней:
prefix_hash = [0] * (n + 1)
power = [1] * (n + 1)
4. Для каждого символа строки проводим хеширование через рекуррентную формулу:
for i in range(n):
prefix_hash[i+1] = (prefix_hash[i] * p + (ord(s[i]) - ord('a') + 1)) % MOD
power[i+1] = (power[i] * p) % MOD
5. Вычисление хеша для подстроки (i : i + k) :
h = (prefix_hash[i+k] - prefix_hash[i] * power[k]) % MOD
6

7.

Задача 1. Подстроки
План решения
1.
2.
3.
4.
5.
Предварительный расчет префиксных хешей
Осуществляем перебор всех длин подстрок, начиная с самой большой
Для каждой длины подстрок считаем частоты хешей (можно использовать словарь), а также
поддерживаем максимальную частоту
Вычисляем вес (максимальная частота, умноженная на длину подстроки)
Проверяем/обновляем максимум
7

8.

Задача 1. Подстроки
План решения
1.
2.
3.
4.
5.
Предварительный расчет префиксных хешей
Осуществляем перебор всех длин подстрок, начиная с самой большой
Для каждой длины подстрок считаем частоты хешей (можно использовать словарь), а также
поддерживаем максимальную частоту
Вычисляем вес (максимальная частота, умноженная на длину подстроки)
Проверяем/обновляем максимум
Возможность оптимизаций:
- если текущий возможный максимум (n - L + 1) * L меньше уже найденного max_weight, можно
выходить из цикла, так как дальнейшие L не улучшат результат.
- цикл в п. 3 можно вести до (n - L + 1), так как индекс (n - L) будет указывать на начала
последней подстроки
8

9.

Задача 9. Совпадения
Дана непустая строка S. Нужно найти такое наибольшее число k и строку
t, что s совпадает со строкой t, выписанной k раз подряд
Описание входных данных
Одна строка длины N, (1 ⩽ N ⩽ 6∗105), состоящая только из маленьких
латинских букв.
Описание выходных данных
Вывести k и строку t.
Входные данные: abcabcabcabc
Выходные данные: 4 abc
9

10.

Задача 9. Совпадения
План решения
1. Предварительный расчет префиксных хешей
2. В цикле проверяем периодичность строки, перебирая возможные длины периода (до n // 2
+1)
1. Период проверяем только у длин, кратных длине строки
2. Проверка периодичности периода d заключается в следующем:
1. Считаем начальный хеш подстроки (первой от начала строки)
2. В цикле считаем хеши последующих подстрок (d * i)
1. Если начальный хеш не совпадает с текущим, то периодичности нет
2. Иначе смотрим следующую подстроку
3. Если цикл завершился, то строка действительно периодична
3. Считаем, сколько раз делит исходную строку длина подстроки
4. Вывод количество, и саму подстроку
10

11.

Задача 10. Привидение Ваня
Привидение Ваня любит играть со своими плитками. Он любит выкладывать их в
ряд и разглядывать свое творение. Однако недавно друзья решили подшутить над
Ваней и поставили в его игровой комнате зеркало. Ведь всем известно, что
привидения не отражаются в зеркале! А плитки отражаются. Теперь Ваня видит
перед собой N цветных плиток, но не знает, какие из этих плиток настоящие, а какие
— всего лишь отражение в зеркале. Помогите Ване! Выясните, сколько плиток может
быть у Вани. Ваня видит отражение всех плиток в зеркале и часть плиток, которая
находится перед ним. Часть плиток может быть позади Вани, их он не видит.
11

12.

Задача 10. Привидение Ваня
12

13.

Задача 10. Привидение Ваня
Описание входных данных
Первая строка входного файла содержит число N (1⩽ N ⩽106) и количество различных цветов, в
которые могут быть раскрашены плитки — M (1⩽M⩽106). Следующая строка содержит N целых
чисел от 1 до M — цвета плиток
Описание выходных данных
Выведите в выходной файл все такие K, что у Вани может быть K плиток в порядке убывания.
13

14.

Задача 10. Привидение Ваня
# input
n, m = 6, 2
a = [1, 1, 2, 2, 1, 1]
# expected
ans = [6, 5,3]
14

15.

Задача 10. Привидение Ваня
План решения
1. Необходимо убедится, что Ваня видит палиндром
2. Для определения палиндрома, необходимо рассчитать прямой и обратные
префиксные хеши
3. Для всех вариантов до n // 2 + 1:
1. Берем исходный прямой хеш i (предполагаемое количество плиток)
2. Берем обратный хеш для следующего отрезка
1. Начало: n-2i
2. Конец n-i (обратная сторона)
3. Длина отрезка: i (n – i – n + 2i)
3. Если хеши совпадают, то добавляем n-i в результирующий список
15

16.

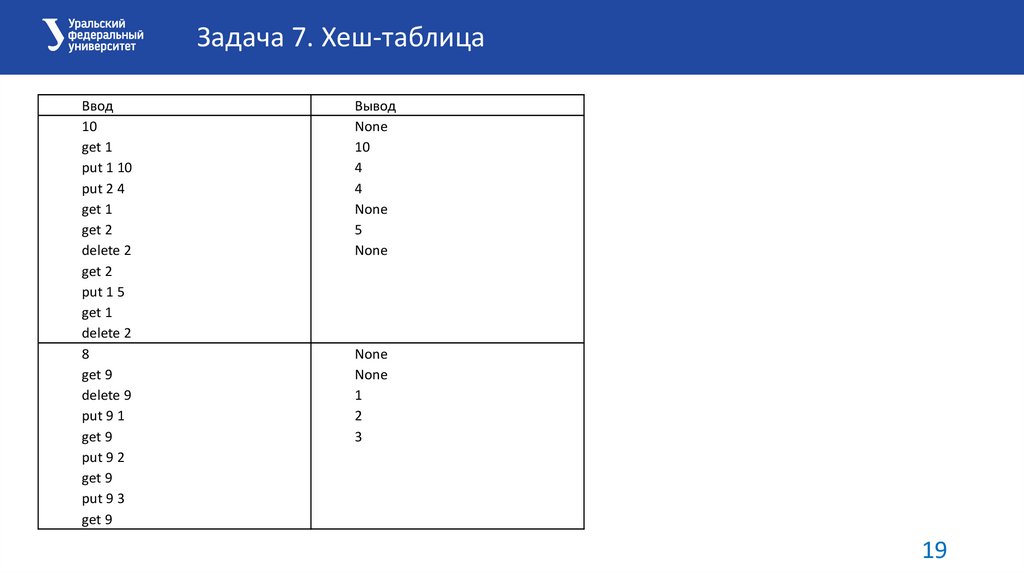
Задача 7. Хеш-таблица
Тимофей, как хороший руководитель, хранит информацию о зарплатах своих
сотрудников в базе данных и постоянно её обновляет. Он поручил вам написать
реализацию хеш-таблицы, чтобы хранить в ней базу данных с зарплатами
сотрудников.
Хеш-таблица должна поддерживать следующие операции:
put key value – добавление пары ключ-значение. Если заданный ключ уже есть в
таблице, то соответствующее ему значение обновляется.
get key – получение значения по ключу. Если ключа нет в таблице, то вывести
«None». Иначе вывести найденное значение.
delete key – удаление ключа из таблицы. Если такого ключа нет, то вывести
«None», иначе вывести хранимое по данному ключу значение и удалить ключ.
16

17.

Задача 7. Хеш-таблица
В таблице хранятся уникальные ключи.
Требования к реализации:
• Нельзя использовать имеющиеся в языках программирования реализации хештаблиц (std::unordered_map в C++, dict в Python, HashMap в Java, и т. д.)
• Число хранимых в таблице ключей не превосходит 105.
• Разрешать коллизии следует с помощью метода цепочек или с помощью
открытой адресации.
• Все операции должны выполняться за O(1) в среднем.
• Поддерживать рехеширование и масштабирование хеш-таблицы не требуется.
• Ключи и значения, id сотрудников и их зарплата, – целые числа. Поддерживать
произвольные хешируемые типы не требуется.
17

18.

Задача 7. Хеш-таблица
Формат ввода
В первой строке задано общее число запросов к таблице n (1 ≤