Похожие презентации:
Магнит резонансты әдістер эпр-спектроскопиясы 6-дәріс
1. МАГНИТ РЕЗОНАНСТЫ ӘДІСТЕР ЭПР-спектроскопиясы
6-дәріс.2.
3.
Магнитрезонансты әдістер көмегімен зат және сәуленің магниткомпонентасының
әрекеттесуін
зерттейді.
Оларға
радиоспектроскопияның екі әдісі жатады – ядролық магниттік
резонанас (ЯМР) және электрондық магниттік резонанас
(ЭПР). Осындай спектрлердегі ауысуларға сәйкес келетін
энергия айырымы өте кіші (жиіліктері 40 МГц-тен 10000 МГцке дейінгі радиодиапазонында жатады). Демек бұл әдістердің
айыру қабілеті және сипаттаушы уақыттары жоғары, бірақ
сезімталдықтары төмен. Бұдан басқа әрекеттесулерге
қатысатын энергия деңгейлері меншікті емес, себебі олар тек
сыртқы магнит өрісінде пайда болады, бұл деңгейлер
бөлшектердің химиялық құрылысына тәуелді. Магнит
резонанасты әдістердің физикалық негіздерін тұрақты магнит
моменті бар бөлшектер (атомдар, молекулалар, иондар) кіретін
жүйе мен айнымалы электромагнит өрісінің энергиясын
резонанасты жұту құрайды. Мұндай бөлшектер парамагнитті
бөлшектер деп аталады.
4.
Эффект жүйенің сыртқы магнит өрісіндегі энергия деңгейлерініңазғындауы жойылғандықтан болатын бөлшектердің магнит моменттерінің
кеңістікте әртүрлі бағытталу нәтижесінде байқалады. Бөлінген деңгейлер
арасында (Зееман деңгейлері) жұтудан пайда болатын ауысулар басталады.
Егер ауысулар атом ядроларының магнит моменттерімен байланысты
деңгейлер арасында жүретін болса, құбылыс ЯМР деп аталады. Ауысулар
электрондардың магнит моменттерінің әртүрлі бағытталуымен байланысты
деңгейлеріне негізделген болса, құбылыс ЭПР деп аталады.
Электрондардың магнит моменттері ядролардікінен бірнеше ондық ретке
үлкен, осы себептен ЭПР сигналы ЯМР сигналынан интенсивті. Бірақ
атомдардың электрон қабықшаларының толықтырылған жағдайында
электрондардың
магниттік
және
механикалық
моменттері
компенсацияланады. Демек, электрондардың магнит моменттерімен
байланысты резонанасты құбылыстар тек жұптаспаған электрондары бар
бөлшектерде байқалуы мүмкін.
5.
ЭПР құбылысының физикалық негіздері. g-факторжәне оның қасиеттері
ЭПР спектроскопиясы әртүрлі химиялық мәселелерді
шешуде кең қолданылады. Осы әдістің негізгі құндылығы –
жұптаспаған электрондары бар бөлшектердің өте кіші
концентрацияларын байқау, өлшеу және олардың энергиялық
күйлері мен локализациясын сипаттауына мүмкіндік
беретінімен байланысты. Үлгі осындай талдау әдісін
қолданғанда бұзылмайды да, өзгермейді де. Жұптаспаған
электрондары бар бөлшектер химиялық реакциялар өтетін
жүйелерде өте маңызды роль атқарады, себебі, олардың
химиялық активтігі өте жоғары. Сондықтан оларды байқау көп
жағдайда реакция механизмін анықтауға жол ашады. ЭПР
құбылысын Ресей ғалымы Е.К.Завойский 1944 жылы ашқан.
6.
Жұптаспаған электрондары бар бөлшектерге кейбір атомдар,иондар, бос радикалдар, триплетті күйдегі молекулалар
жатады, оларды екі топқа бөлуге болады:
1) жұптаспаған электроны бір атоммен байланысты: (Н, О,
галоген атомдары, Fen+, Con+, Nin+ ауыспалы элементтердің
иондары, жартылай өткізгіштер);
2) жұптаспаған электрон бүтіндей молекуламен немесе оның
үлкенірек бөлігімен байланысты (бос радикалдар, ионрадикалдар, триплетті қоздырылған молекулалар).
7.
g-фактор. Атомда бір жұптаспаған электроны бар, ядроның моменті нольгетең қарапайым жағдайды қарастырайық. Мұндай атомның магниттік
қасиеттері жұптаспаған электронның орбиталдық магниттік және
компенсацияланбаған спиндік магниттік моменттерімен анықталады.
Орбиталдық моменттің жартылай классикалық моделі ретінде ядроның
айналысында ω бұрыштық жиілігімен айналатын заряды е электронды
ұсынады, мұндай айналу магнит моментін тұғызатын i=eω/(2π) айнымалы
тоққа эквивалентті,
iS
eω
e
2
μ
πr
ωr 2
c
2 πc
2c
мұндағы с – жарық жылдамдығы; r – электрон орбитасының радиусы; S –
орбитамен қоршалатын аудан. Қозғалыс мөлшерінің механикалық моменті
Pl=mωr2, мұнда m – электронның массасы. Орбиталды магнит моментінің
механикалық моментіне қатынасы (гиромагнитті қатынас) gl немесе
орбиталдық магнетизмнің g-факторы (спектроскопиялық ыдырау факторы)
деп аталады:
l
e
gl
Pl
2mc
e/(2mc) бірлігінде gl =1 аламыз.
8.
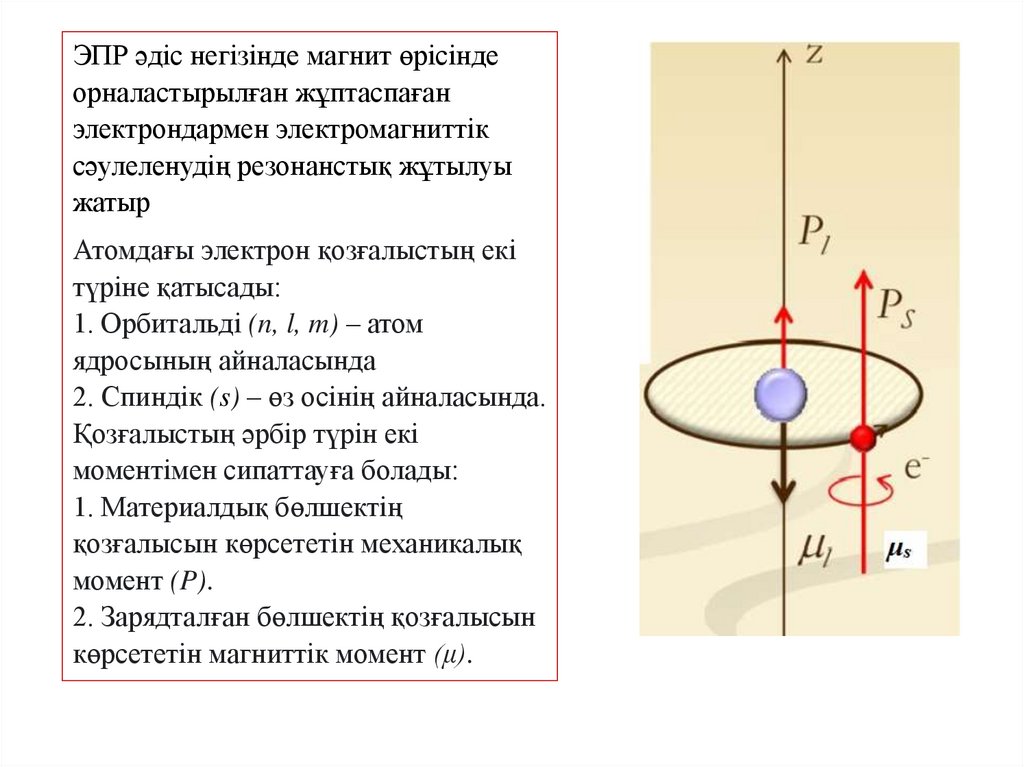
ЭПР әдіс негізінде магнит өрісіндеорналастырылған жұптаспаған
электрондармен электромагниттік
сәулеленудің резонанстық жұтылуы
жатыр
Атомдағы электрон қозғалыстың екі
түріне қатысады:
1. Орбитальді (n, l, m) – атом
ядросының айналасында
2. Спиндік (s) – өз осінің айналасында.
Қозғалыстың әрбір түрін екі
моментімен сипаттауға болады:
1. Материалдық бөлшектің
қозғалысын көрсететін механикалық
момент (P).
2. Зарядталған бөлшектің қозғалысын
көрсететін магниттік момент (μ).
9.
Кванттық механикаға сай:Pl l (l 1) ,
l l (l 1)
мұндағы l – орбиталық кванттық саны;
e 9,27 10 24 A m2
2mc
Бор магнетоны, оның мәні электронның орбиталдық
магниттік моментінің кіші мәніне, яғни сутек атомындағы
электронның бірінші Бор орбитасындағы моментіне тең;
2 -ге бөлінген Планк тұрақтысы. Осыдан:
l
e
gl
Pl
2mc
10.
Спиндік магнетизм үшін:s 2 s ( s 1) ;
Ps s(s 1)
мұнда s-спиндік кванттық сан (электрон үшін s=1/2).
S e
gS
PS mc
яғни (e/(2mc) бірлігінде) спиндік магнитизмнің g -факторы
gs =2 (дәлірек, релятивистік түзетуді ескергенде, бос электрон
үшін Ланде g -факторы тең болады 2,0023).
11.
Спин-орбитальді байланыс бар кезде атомның толық магнитмоменті құраушылардың екеуінің де векторлық қосындысының
нәтижесі болып табылады да, g -фактордың мәні аралық
болады.
Спин-орбиталды байланыс электронның спиндік магнит
моментінің осы электронның орбитальді қозғалысынан пайда
болатын магнит өрісімен әрекеттесуінің нәтижесі болып
табылады. Бір жұптаспаған электрон моделіне ядроның заряды
Ze үшін әрекеттесу энергиясы:
ze2
E 2 2 2 s l s l
mc r
Сонымен, Z өсуімен E өседі, Е орбиталді моментке және
орбиталы түріне, яғни r радиусіне тәуелді. λ-нің мәнін нақты
атомдық жүйесі үшін оптикалық спектрлерінен табуға болады.
12.
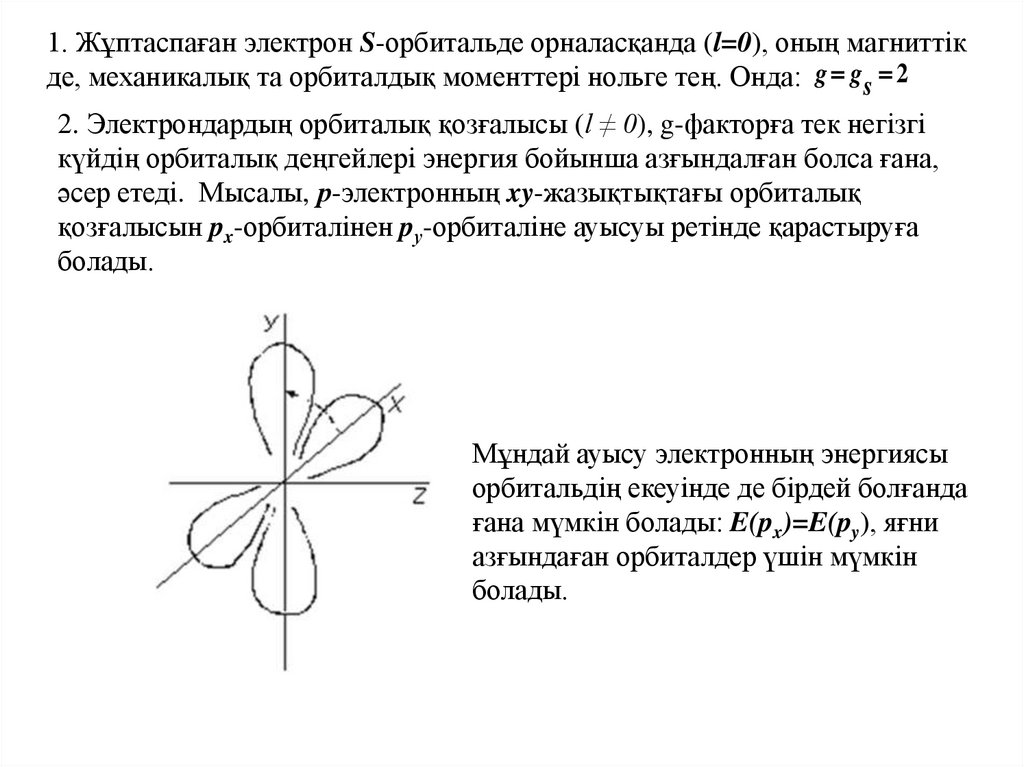
1. Жұптаспаған электрон S-орбитальде орналасқанда (l=0), оның магниттікде, механикалық та орбиталдық моменттері нольге тең. Онда: g g s 2
2. Электрондардың орбиталық қозғалысы (l ≠ 0), g-факторға тек негізгі
күйдің орбиталық деңгейлері энергия бойынша азғындалған болса ғана,
әсер етеді. Мысалы, р-электронның xy-жазықтықтағы орбиталық
қозғалысын px-орбиталінен pу-орбиталіне ауысуы ретінде қарастыруға
болады.
Мұндай ауысу электронның энергиясы
орбитальдің екеуінде де бірдей болғанда
ғана мүмкін болады: E(px)=E(py), яғни
азғындаған орбиталдер үшін мүмкін
болады.
13.
Спиндік және орбитальдік моменттер өзара әрекеттеседі, жұптаспағанэлектрондардың күйі толық спиндік S және орбитальдік L моменттерімен
және қорытқы J моментімен бейнеленеді (мұндағы J=L S, таңба электрон
қабықшаның толықтырылуына тәуелді). Бұл жағдайда g - фактордың мәні
1 мен 2-нің арасында жатады да, газды фазадағы бос атомдар үшін немесе
жұптаспаған электрондар ішкі қабықшаларда орналасқанда Ланде
формуласы арқылы есептеледі:
g 1
J ( J 1) S ( S 1) L( L 1)
2 J ( J 1)
Ланде формуласы жұптаспаған электрондар ішкі қабықшаларда
орналасқанда, мысалы, сирек элементтердің иондары үшін орындалады.
Мұндай электрондардың сипаттамасы, көп жағынан, ортамен
әрекеттеспейтін, бос электрондардікіндей болады.
14.
Егер парамагниттік бөлшектер қоршаған орта бөлшектерімен жасалғантөмен симметриялы электр өрістерінде болса (мысалы, Cu және Fe
тұздарында), онда орбиталдық азғындау жойылады да, g-фактордың мәні
gs =2, бұл жағдайда Ланде формуласын пайдалануға болмайды. Бірақ
орбиталдардың энергия айырымы өте үлкен болғанда да, орбиталдық
қозғалыстың ықпалы толық жойылмайды (бұл белгілі «туннель»
эффектісіне негізделеді). Сонымен, g -фактор спиндік мәніне тең
болмайды, оны келесі формула арқылы есептеуге болады:
a
g g s 1
E
мұнда λ– Рассел-Саундерстің спин-орбиталдық байланыс тұрақтысы,
Δ E– негізгі және оған ең жақын орбиталь күйлерінің энергия айырымы, а
– парамагниттік бөлшектің табиғатын және бөлшектің магниттік моменті
мен сыртқы магниттік өріс векторларының өзара бағытталуына тәуелді
көбейткіш.
15.
g -фактордың анизотропиясы.Магнит өрісі әртүрлі бағытталғанда
орбиталды қозғалысқа әртүрлі
орбиталдар қатысады да, g фактордың мәні магниттік өрістің
бағытына тәуелді болу керек. Бұл
құбылыс g -фактордың кеңістік
анизотропиясы деп аталады. Оны
нитроксил радикалының >N-O*
фрагменті мысалында қарастырайық.
g x g s (1 / E n * )
g y g s ( 1 λ / Eσπ )
g z = g s.
Сонымен, g-фактордың кеңістік
анизотропиясының маңызы – оның мәні В
индукцияның бағыты мен молекулалық
осьтерінің арасындағы бұрыштарына
тәуелді. Жалпы жағдайда:
g g x2 cos2 ( B x) g 2y cos2 ( B y) gz2 cos2 ( B z)
мұнда g - екінші рангты тензор; gX, gY, gZ - оның негізгі мәндері.
16.
Бөлшектердің g-факторының анизотропиясын реттелгенорталарда, мысалы, қатты матрицаларда, монокристалдарда
байқауға болады. Сұйықта бөлшектердің ретсіз жылулық
қозғалысына байланысты g факторының орташа мәні ғана
анықталады. g-фактордың тәжірибелік мәні парамагниттік
бөлшектің «сапасын» сипаттайтын болады.
17.
Егер g факторы 2,00232 болса, онда біз бос электрондарменжұмыс істейміз. Көптеген бос радикалдардағы жұптаспаған
электрон үшін g- факторы да осы мәнге жақын және одан тек
үтірден кейінгі екінші немесе үшінші таңбада ерекшеленуі
мүмкін. Ауыспалы элементтердің қосылыстарында
g- факторының мәні кең ауқымда өзгереді (бірнеше бірлікке
дейін). g - факторының ауытқуы оң немесе теріс болуы
мүмкін. Спин-орбиталық әрекеттесу неғұрлым күшті болса,
оның абсолютті мәні соғұрлым үлкен болады.
g-фактордың мәні мен таңбасы (изотропты жүйелерде) немесе
g-тензордың компоненттер (анизотропты ортада) бойынша
парамагниттік бөлшектің заряды мен электрон тығыздығының
таралуын бағалауға болады.
18.
Тіпті g факторы таза спиндік мәнге жақын органикалықрадикалдарда да оң және теріс радикал иондарын оның мәні
бойынша ажыратуға болады: g факторы теріс иондар үшін
көбірек.
KCl матрицасында молекулалық оттегі ионы үшін О2- g = 2,114,
ал О2+ ион-радикал үшін g = 2,018; азот диоксиді радикалы
үшін NaNO2 матрицасында NO2 g = 1,9994, ал KNO3
матрицасындағы NO2- ион-радикал үшін g = 2,007.
Эксперименттік деректер g факторының 1,9-дан 4,0-ге дейінгі
мәндерді қабылдай алатынын көрсетеді. Осылайша, gфактордың таза спиндік мәннен ауытқуы молекуланың
(парамагнитті бөлшек) құрылымына байланысты жоғары да,
төмен де болуы мүмкін. Мысалы, сутегі атомы үшін g =
2,00226; NO2 үшін g = 1,999, ал ClO2 үшін g = 2,01. Осылайша,
g факторының мәнін пайдалана отырып, белгілі бір дәрежеде
парамагниттік бөлшектерге сапалық талдау жүргізуге немесе
олардың кейбір қасиеттерін болжауға болады.
19.
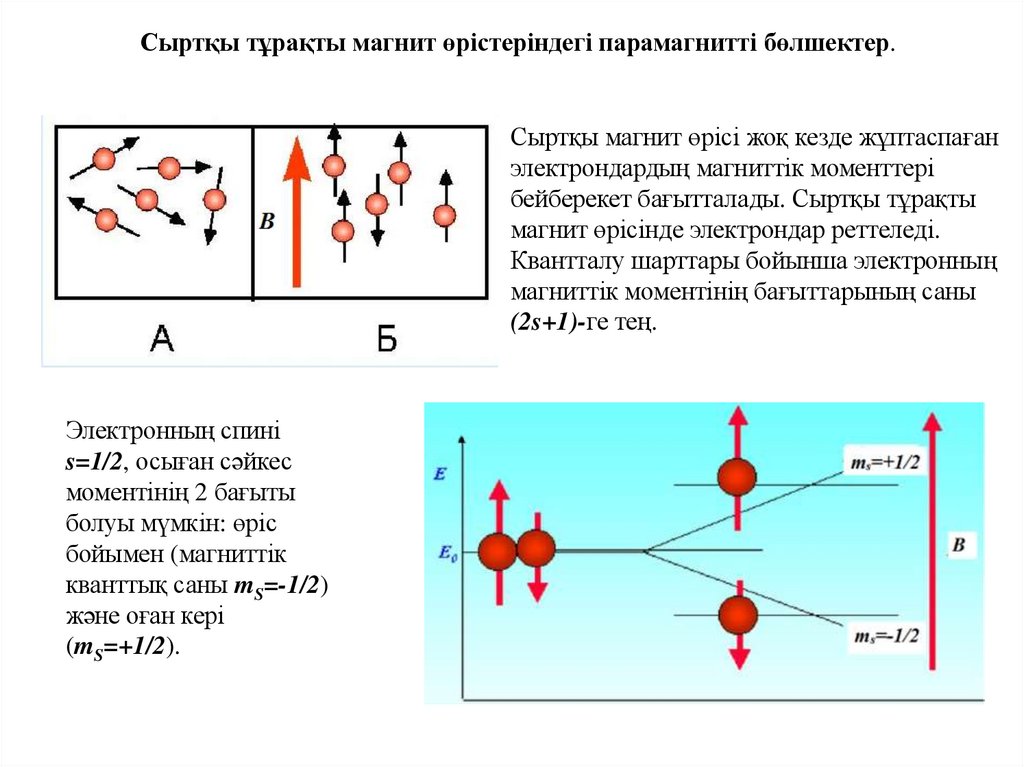
Сыртқы тұрақты магнит өрістеріндегі парамагнитті бөлшектер.Сыртқы магнит өрісі жоқ кезде жұптаспаған
электрондардың магниттік моменттері
бейберекет бағытталады. Сыртқы тұрақты
магнит өрісінде электрондар реттеледі.
Квантталу шарттары бойынша электронның
магниттік моментінің бағыттарының саны
(2s+1)-ге тең.
Электронның спині
s=1/2, осыған сәйкес
моментінің 2 бағыты
болуы мүмкін: өріс
бойымен (магниттік
кванттық саны mS=-1/2)
және оған кері
(mS=+1/2).
20.
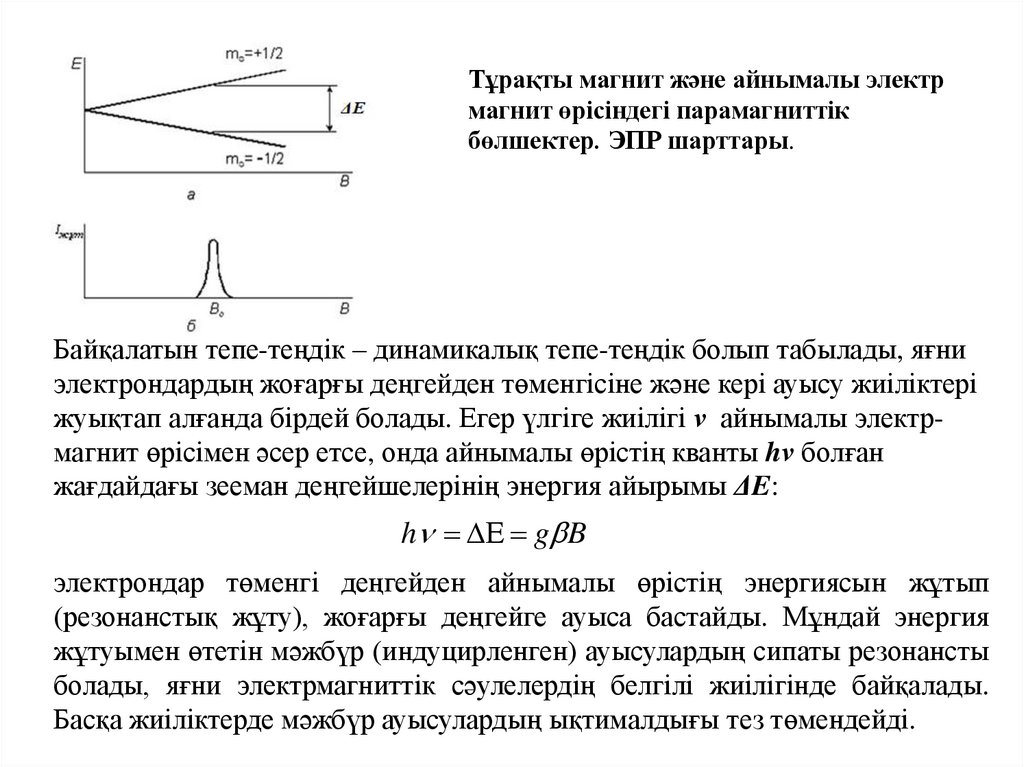
Өріс z-осі бойынша бағытталған болса, яғни ћ бірлігі квант санына ms теңP
болатын электронның толық механикалық моменті s орнына оның
проекциясын Pz есепке алу керек, электронның магниттік моменті пен
сыртқы магнит өрісі В-нің өзара әрекеттесу энергиясы үшін былай жазуға
болады:
E μ s B gβPz B gβBm s
E E2 E1 g B(mS 2 mS1 ) g B
21.
Өз бетінше қарау үшін қосымша материал:22.
Тепе-тендік күйде Больцман таралуы бойынша бөлшектің саныexp(E/kT)-ге пропорционалды. Төменгі E1 деңгейде спиндер өріске кері
бағытталған (яғни моменттері өріс бойымен), бұл деңгейдің толықтырылуы
былай жазылады:
1 g B
1 g B
N exp
N exp
2
kT
2 kT
Әдетте В=0,3 Тл, Т>10 К, ΔE <<kT.
Соңғы теңдіктегі экспонентаны қатарға жіктеп табамыз:
N
1
kT
N т т.
мұндағы, N = N+ + N- – парамагниттік бөлшектердің толық саны, n0=(N- - N+)т-т
– тепе-теңдіктегі деңгейлердің толықтырылу айырымын белгілеп, табамыз:




















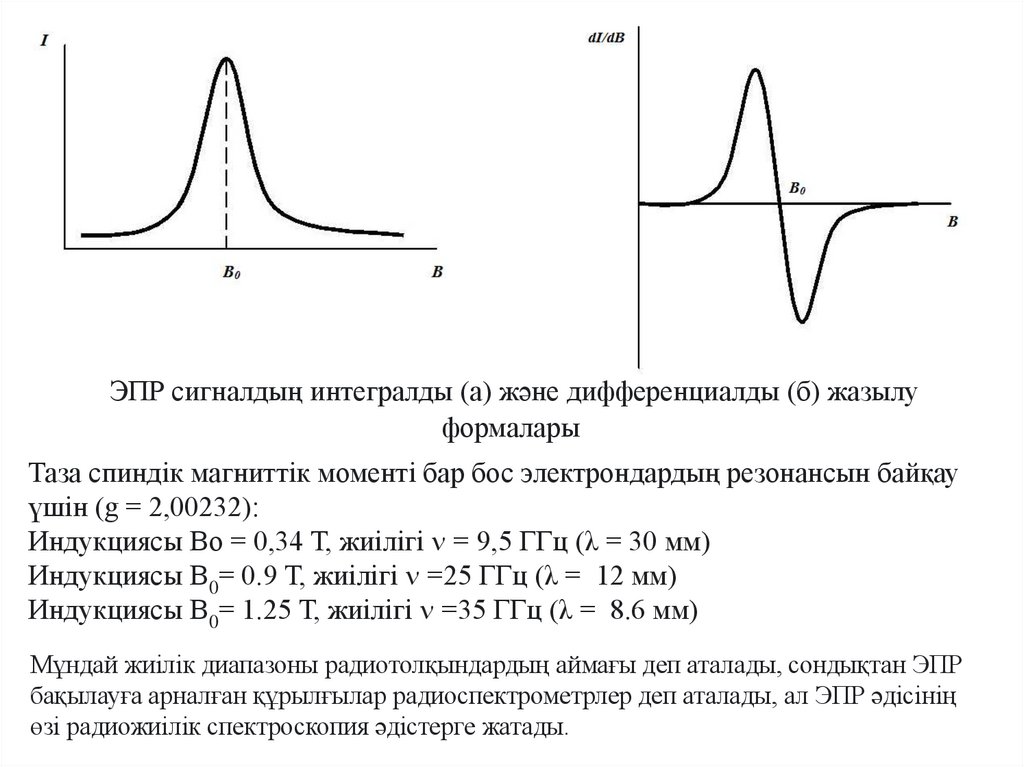






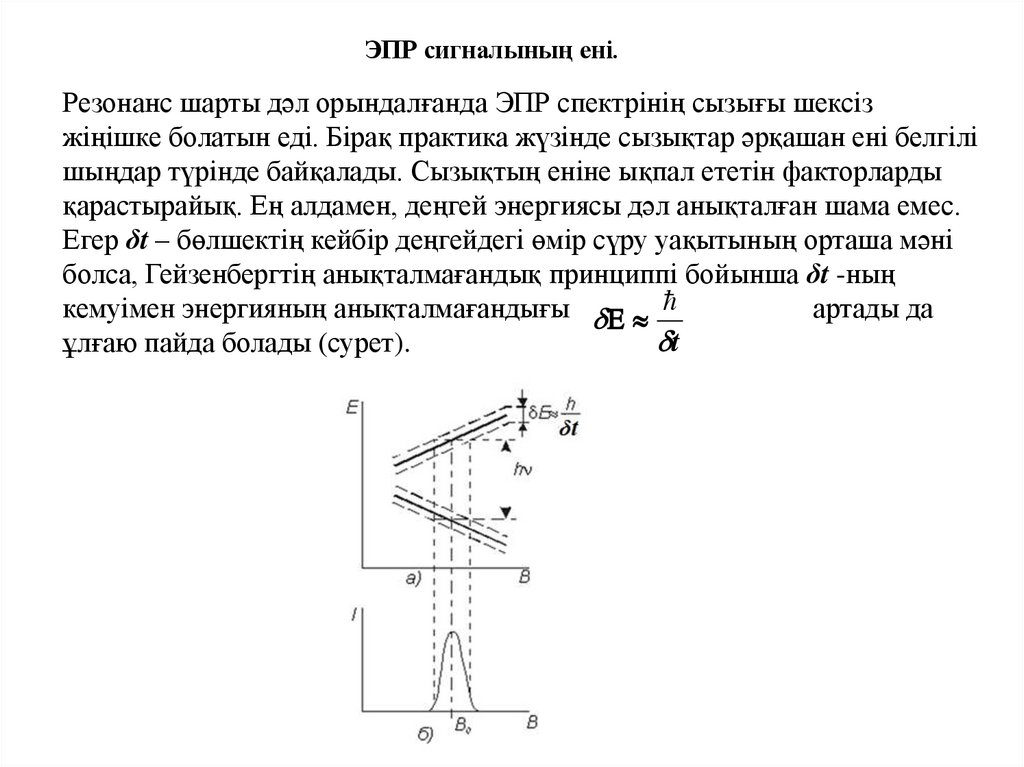


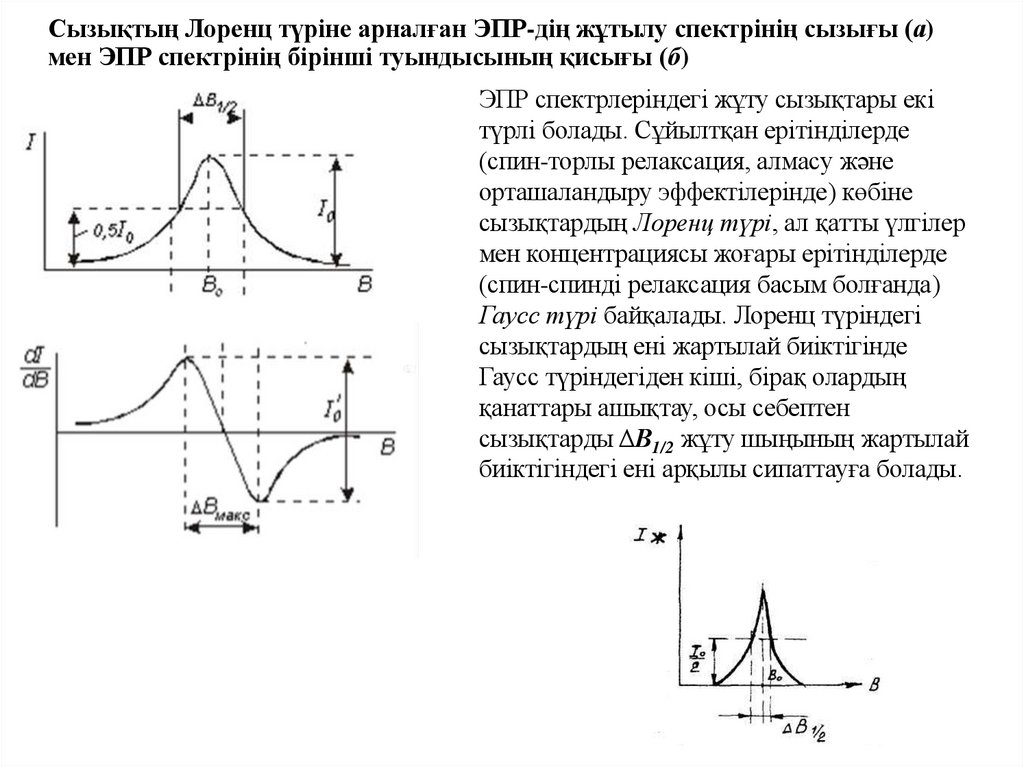




 Физика
Физика








