Магнит. Магнит өріс бағыты

1.

1. МАГНИТ
ӨРІСІ
1820 жылы дат физигі Х.Эрстед тогы бар
өткізгіштердің магнит стрелкасына әсерін
байқап, оны магнит өрісі деп атады. Магнит
өрісін тогы бар раманың көмегімен
зерттеуге болады. Нормальдің оң бағыты
Тогыережесі
бар раманы
магнит
токпен
оң бұрғы
бойынша
анықталады.
өрісіне енгізгенде, магнит өрісі
n
мен нормаль бағыттары бірбірімен дәл келмесе, контурды
тепе-теңдік
жағдайға әкелуге
тырысатын раманы
І
айналдыратын күш моменті
пайда болады. Айналу күш
моментінің
шамасы
нормаль
Бұл момент
болғанда,
максималь
мәнге
2
магнит өріс бағыты
ие болады. Mмен
max ~ І S .
арасындағы - бұрышына
Контурдың магнит моменті : P = І·S ,
тәуелді.
векторлық түрде
Pm IS n.
(1.1)
1

2.

Күштердің айналдыру моменті :
M Pm B ,
(1.2)
B
мұндағы
– магнит индукция векторы, ол
өрісті сандық мөлшер түрінде сипаттайды.
B M Pmконтурға
Берілген өріс нүктесінде әртүрлі
мөлшерлері әртүрлі айналдырушы моменттер
әсер етеді, бірақ та
қатынасы барлық
контурлар үшін бірдей шама, сондықтан ол
Магнит
өрісінің
берілген
нүктедегі магнит
шама
магнит
өрісінің
сипаттамасын
беретін
индукциясы
деп магнит
моменті бірге тең
магнит
индукциясы
деп аталады:
рамаға әсер етуші максималь айналдырушы
моментті айтады.
Магнит өрісі - күш өрісі болып табылады,
сондықтан оны
магнит индукция
сызықтарыменB өрнектеуге болады, ол
сызықтардың әр нүктелеріне жүргізілген
жанамалар
векторымен
Индукция сызықтарының
бағытын өзімізге бағыттас
болады.
белгілі бұрғы ережесі немесе оң қол
ережесі бойынша анықтауға болады.
A
B
C
2

3.

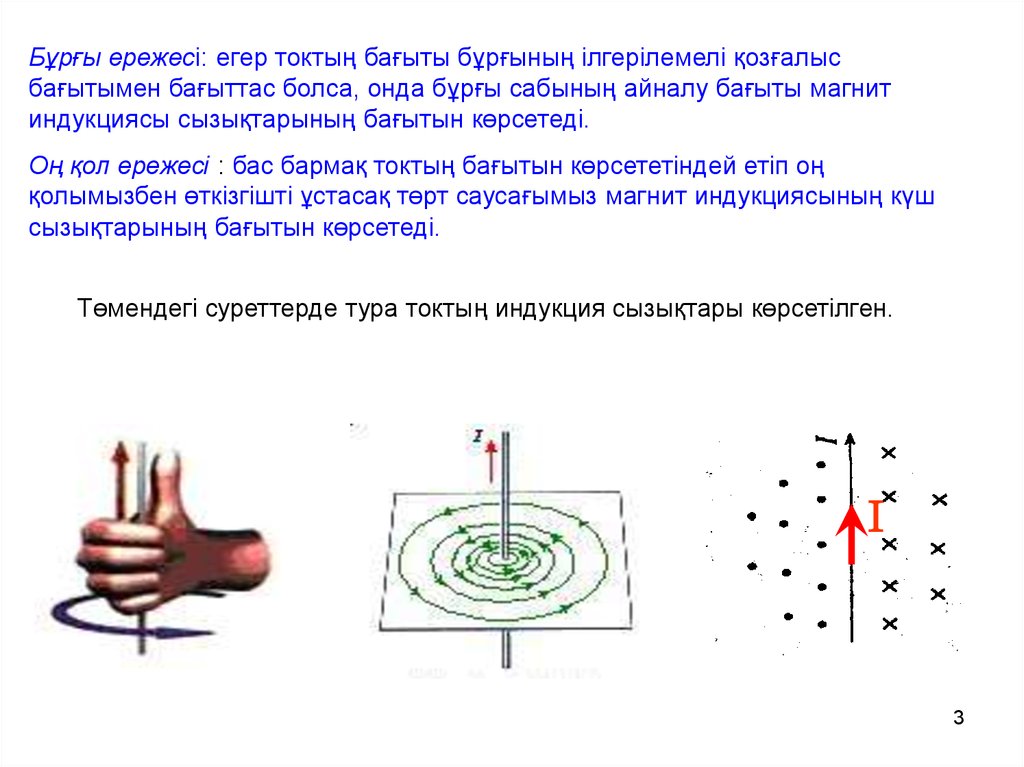
Бұрғы ережесі: егер токтың бағыты бұрғының ілгерілемелі қозғалыс
бағытымен бағыттас болса, онда бұрғы сабының айналу бағыты магнит
индукциясы сызықтарының бағытын көрсетеді.
Оң қол ережесі : бас бармақ токтың бағытын көрсететіндей етіп оң
қолымызбен өткізгішті ұстасақ төрт саусағымыз магнит индукциясының күш
сызықтарының бағытын көрсетеді.
Төмендегі суреттерде тура токтың индукция сызықтары көрсетілген.
3

4.

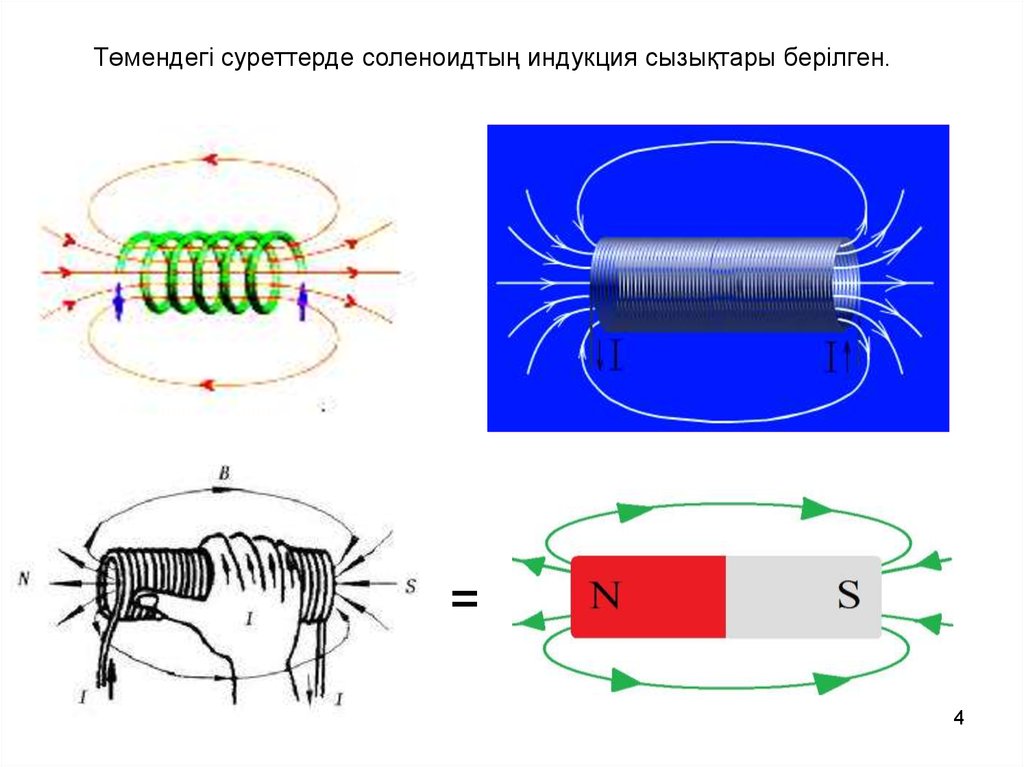
Төмендегі суреттерде соленоидтың индукция сызықтары берілген.
=
4

5.

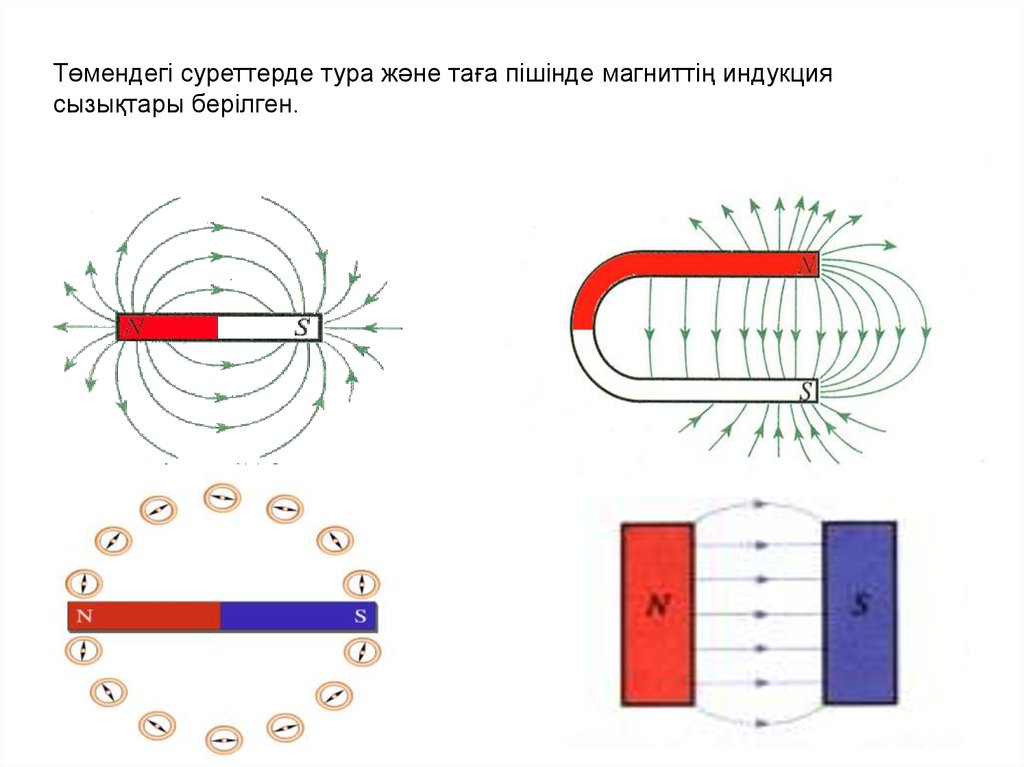
Төмендегі суреттерде тура және таға пішінде магниттің индукция
сызықтары берілген.
5

6.

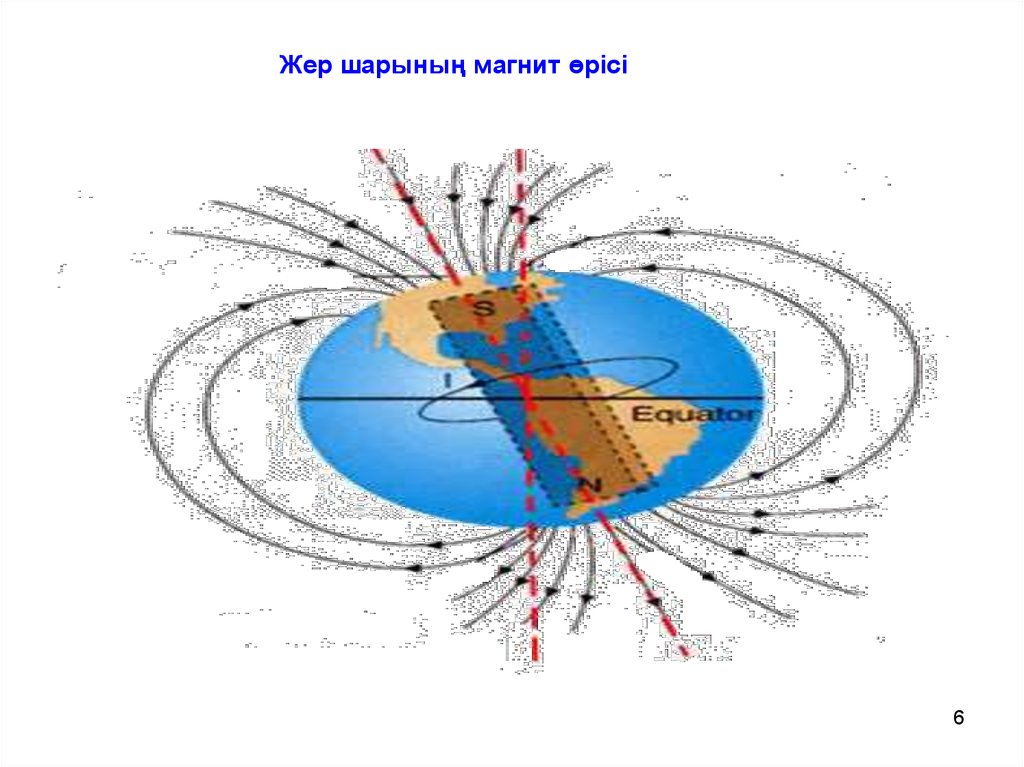
Жер шарының магнит өрісі
6

7.

Магнит өрісінің күш сызықтары тұйық болады, күш сызықтары тұйық өріс
құйынды өріс деп аталады. Электр өрісі – потенциалды өріс (электр өрісінің
сызықтары оң электр зарядтарында басталып, теріс зарядтарда аяқталады).
Магнит өрісінің күш сызықтарының тұйық болуы - табиғатта магнит
зарядтарының жоқ екенін көрсетеді.
Магнит өрісін сипаттау үшін магнит индукциясы векторымен бірге, магнит
өрісінің кернеулігі деп аталатын шама енгізіледі. Біртекті, изотроп орта үшін
олар мына өрнек бойынша байланысты:
B 0 H
(1.3)
H
7 Гн
4
10
м
А2
‒ ортаның магнит өтімділігі. Вакуум үшін = 1-ге тең.
7
мұндағы 0 ‒ магнит тұрақтысы, 0 4 10
7

8.

1.1 Био-Савар-Лаплас заңы және оны қолдану
1820 жылы француз ғалымдары Био және Савар әртүрлі пішінді токтардың
магнит өрістерін зерттеу арқылы, магнит өрісінің инукциясы B өрісті туғызатын
токқа І тура пропорционал болып, индукциясы анықталатын нүктеге дейінгі
арақашықтыққа тәуелді болатынын анықтады. Тәжірибеден алынған
нәтижелерді тұжырымдап, Лаплас ұзындығы dl ток элементі туғызатын өріс
индукциясын анықтайтын өрнекті тапты.
I dl r
0
dB
4
r3
I
dB
d
r
(1.1.1)
мұндағы d - токтың элементар бөлігімен
бірдей болатын және ток ағатын бағыт бойынша
бағытталған элементар ұзындық.
r
- магнит индукциясы анықталатын нүктеге
ток элементінен жүргізілген радиус-вектор .
8

9.

Магнит индикция векторын модулі бойынша жазатын болсақ:, онда
dB
мұндағы –
0 Idl
sin ,
2
4 r
(1.1.2)
dl мен r арасындағы бұрыш.
Био-Савар-Лаплас заңы тогы бар өткізгіштің маңындағы кез келген
нүктенің магнит өрісінің шамасын анықтайтын заң болып табылады.
Магнит индукция векторының B бағыты оң қол ережесі немесе бұрғы
ережесі бойынша анықталады.
Магнит өрісі үшін суперпозиция принципі: бірнеше токтар туғызған магнит
өрісінің қорытқы мәні әрбір ток туғызған өрістердің магнит индукцияларының
векторлық қосындысына тең:
n
B Bi
i 1
9

10.

1. Шексіз ұзын түзу тогы бар өткізгіш
туғызатын магнит өрісінің индукциясы
Тогы бар өткізгіштен R қашықтықта орналасқан А
нүктедегі индукцияны анықтайық. Индкуция векторы
бағыты тақта жазықтығына перпендикуляр (“бізге
қарай”) болады(оң қол ережесі бойынша).
R
r
,
sin
rd
dl
sin
0 I sin
dB
d
4 R
Өрнегін БиоСавар-Лаплас
теңдеуіне қойсақ,
және Шексіз ұзын,
тура токтың
барлық
элементтері
бұрышы 0 үшін
дейін
ден π-ге
0 2I
sin d
өзгереді,4 R
0
сондықтан:
0 I
B dB
4 R
Сонымен, тура токтың магнит индукциясы:
0 I
B
2 R
(1.1.3)
10

11.

2. Тогы бар дөңгелек өткізгіштің центріндегі магнит индукциясы
барлық ток элементтерінің дөңгелек ток центріне дейінгі
қашықтығы бірдей және ол R радиусқа тең.
Био-Савар-Лаплас заңы бойынша :
0 I
dB
dl ,
2
4 R
0 I 2 R
I
B dB
dl
0
2R
4 R 2 0
Дөңгелек ток центріндегі
магнит индукциясы:
I
B 0
2R
(1.1.4)
11

12.

1.2 Магнит өрісінің тогы бар
өткізгіштерге әсері (Ампер заңы)
Магнит өрісінің тогы бар өткізгішке әсер ететін күшін Ампер күші деп
атайды. Ампер заңының математикалық өрнегі:
d F I dl B
(1.2.1)
мұндағы І – ток күші, B – dl элементі
орналасқан нүктедегі магнит
индукциясы.
Ампер күші әруақытта dl және B
векторлары жатқан жазықтыққа
перпендикуляр болады.
Сол қол ережесі: Егер B векторы сол
қолдың алақанына перпендикуляр еніп,
төрт саусақ өткізгіштегі ток бағытымен
бағыттас болса, онда бас бармақ Ампер
күшінің бағытын көрсетеді.
Ампер күшінің модулі
былай
dF IdlB sin
болады:
dl
B
мұндағы және
арасындағы бұрыш.
(1.2.2)
векторлары
12

13.

Ампер заңының көмегімен екі параллель, шексіз ұзын тура токтардың әсерлесу
күшін анықтауға болады .
df 1 B2 I 1dl1
df 2 B1 I 2 dl 2
0 I2
B2
2 a
0 I1
B1
2 a
B2
Екі токтың dl элементар
бөлігіне әсер ететін
күштер df1 = df2
df1 0 I 1 I 2
dl1
2 a
0 I1 I 2
df 2
dl 2
2 a
Idl1
I1
a
df1
df 2
I2
Idl2
B1
13

14.

Ампер заңы сонымен бірге, магнит индукциясының (В) өлшем бірлігін
анықтауға мүмкіндік береді. Егер тогы бар өткізгіштің элементі магнит
өрісінің бағытына перпендикуляр болса, онда Ампер заңы былай
жазылады: dF=І⋅B⋅dl бұдан
B
dF
Idl
1Тл
1Н
( А м)
Магнит индукциясының өлшемі – тесла (Тл). 1 Тл - өріс бағытына
перпендикуляр орналасқан түзу сызықты өткізгіш арқылы 1А ток ағатын
болса, сол өткізгіштің әр метр ұзындығына 1Н күшпен әсер ететін біртекті
магнит өрісінің магнит индукциясы:
14

15.

1.3 Магнит өрісінің қозғалыстағы зарядқа әсері (Лоренц күші)
Индукциясы B магнит өрісінде жылдамдықпен қозғалатын зарядқа белгілі
бір бағытта күш әсер етеді.
Бұл әсер Лоренц күші деп
аталады. Бұл күш
және
зарядқа q, жылдамдыққа
индукция векторы B шамаларына тәуелді
болады, оның бағыты және B вектролары арқылы анықталады.
Fë q , B
(1.3.1)
Fë q B sin ,
(1.3.2)
Лоренц күшінің модулі:
мұндағы –
және B
векторларының арасындағы бұрыш.
Егер зарядталған бөлшек тыныштық қалыпта (ν =0) болса, онда оған
магнит өрісі тарапынан ешқандай күш әсер етпейді. Магнит өрісі тек қана
қозғалатын зарядтарға әсер етеді.
Лоренц күшінің бағыты сол қол ережесі бойынша анықталады (ток пен оң
заряд бағыты бірдей деп есептегенде). Зарядтың шамасы теріс болса,
Леренц күші басбармаққа қарама-қарсы бағытталған болады.
15

16.

f
v
v
f
v
f
v
f
16

17.

Зарядталған бөлшектің жылдамдығы индукция веторына перпендикуляр
болса, Лоренц күші бөлшектің траекториясына нормаль бағытталады да
центрге тартқыш үдеу пайда болады, бөлшек шеңбер бойлап қозғалады.
Траекторияның радиусы бұл күштердің теңдігімен анықталады:
Fë Fö .ò ,
m 2
q B
, R m
R
q B
(1.3.3)
Бөлшектің шеңбер бойымен қозғалысындағы айналу периоды:
T
2 R
2
m
qB
(1.3.4)
демек, айналу периоды жылдамдыққа тәуелсіз (v << c үшін), тек қана магнит
индукциясы мен меншікті зарядқа кері байланысты.
17

18.

Егер электр мен магнит өрістері бір мезетте болса, зарядталған бөлшекке
әсер ететін Лоренц күші былай болады:
Fë q E q , B
(1.3.5)
1.4 ХОЛЛ ЭФФЕКТІСІ
Сыртқы магнит өрісінің индукция
сызықтарына перпендикуляр
орналастырлыған өткізгіш
пластинаның бойымен тығыздығы j ток
жүргенде, пластинаның шеткі жақтары
арасында потенциалдар айырымы
пайда болады, яғни бағыттарына
перпендикуляр бағытта электр өрісі
пайда болады. Бұл құбылыс Холл
эффектісі деп аталады.
18

19.

Ток тығыздығының j бағыты суреттегідей белгілі болса, оңнан солға қарай
қозғалыс жасайтын электронға әсер ететін Лоренц күші жоғары қарай
бағытталады. Пластинаның жоғарғы жағында – электрондардың молдығы, ал
пластинаның төменгі жағында – электрондардың жетіспеушілігі болады.
Сонымен, пластиналардың арасында төменнен жоғары қарай бағытталған
көлденең электр өрісі пайда болады. Бұл өрістің кернеулігі төмендегідей:
eE
e
e B
a
Ba
немесе
(1.4.1)
мұндағы – Холл эффектісі нәтижесінде пайда болатын көлденең
потенциалдар айырмасы; a – пластинаның ені; – электрондардың
реттелген қозғалысының орташа жылдамдығы.
I a d n e ,
I
adne
(1.4.2)
мұндағы d – пластина қалыңдығы, n – электрондар концентрациясы.
Жылдамдықтың
бұл мәнін жоғарғы теңдеуге қоятын болсақ:
19

20.

IBa
1 IB
adne ne d
IB
R
d
(1.4.3)
1
R – затқа тәуелді Холл тұрақтысы .
ne
Көлденең потенциалдар айырымы ток күшіне І ,
магнит өрісі индукциясына B тура пропорционал
да, пластина қалыңдығына d кері пропорционал.
1.5 Вакуумдағы магнит өрісі үшін B векторының циркуляциясы.
Толық ток заңы.
Вакуумдағы
магнит өрісі үшін толық ток заңы: кез- келген тұйық контур
бойынша B векторының циркуляциясы магнит тұрақтысын 0 осы контурды
қамтитын токтардың алгебралық қосындысына көбейткенге тең болады:
n
Bd l 0 I k ,
(1.5.1)
k 1
мұндағы n – пішіні еркін алынған контур қамтитын тогы бар өткізгіштердің
жалпы саны.
20

21.

1.6 Магнит индукциясы векторының ағыны.
Магнит өрісі үшін Гаусс теоремасы
dS ауданы арқылы өтетін магнит индукциясының вектор ағыны:
dФ B d S Bn dS
(1.6.1)
мұндағы Bn = Bcos - векторы dS ауданының нормаль бағытына түсірілген
проекциясы,
Еркінше алынған бет S арқылы магнит индукциясы векторының ағыны:
Ô B d S Bn dS BdS cos .
S
S
S
Өріс біртекті болса (B=const), ал бет жазық болып және B векторына
перпендикуляр орналасса, онда
Ф В S
(1.6.2)
Ағын өлшеміне вебер (Вб) алынады: 1Вб –
индукциясы 1 Тл біртекті магнит өрісіне перпендикуляр орналасқан
ауданы 1м2 жазық бетті қиып өтетін магнит ағыны.
21

22.

Магнит өрісі үшін Гаусс теоремасы: кез келген тұйық бет арқылы магнит
индукциясы векторының ағыны нөлге тең:
B d S B dS 0
n
S
(1.6.3)
S
Бұл тұжырым табиғатта магнит зарядтарының жоқ екендігін және магнит
индукциясы сызықтарының тұйықтығын көрсетеді.
Магнит өрісінде тогы бар өткізгішті орын ауыстыруда
атқарылатын жұмыс
dA Fdh IB dh IBdS ,
(1.6.4)
Өткізгіш бөлігі dh-қа орын ауыстырғанда,
Ампер күші оң жұмыс атқарады. мұндағы
dS
dS dh
dФ –В dS
(суретте
штрихталған),
ауданын
қиып
өтетін магнит индукциясы векторының ағыны.
Магнит өрісінде тогы бар өткізгішті орын ауыстырғанда істелетін жұмыс - ток
күшін қозғалатын өткізгішті қиып өтетін магнит ағынына көбейткенге тең:
dA = ІdФ .
(1.6.5)
22

23.

1.7 ЗАТТАҒЫ МАГНИТ ӨРІСІ
Магнетиктер деп - магниттік қасиеттері қарастырылатын кез-келген
денелерді айтады .
Магнетиктің бірлік көлеміндегі магнит моментін магниттеліну деп атайды:
n
Pm
j
V
ð
i 1
V
mi
(1.7.1)
мұндағы P m – магнетиктің магнит моменті, ол сан жағынан жеке
молекулалардың магнит
моменттерінің қосындысына тең. Әлсіз өрістерде
магниттелу берілген сыртқы өрістерінің кернеулігіне тура пропорционал:
j æH
(1.7.2)
мұндағы æ – заттың магнит сезімталдығы, ол магнетикті сипаттайтын
өлшемсіз шама.
23

24.

B 0 (1 æ) H
B
H
0 (1 æ)
бұдан
(1.7.3)
( 1 æ ) өлшемсіз шаманы әрпімен белгілеу қабылданған, оны ортаның
магнит өтімділігі деп атайды. 1 æ -ті жоғарғы өрнекке қойсақ:
B 0 H .
(1.7.4)
Магнит сезімталдығы æ 0 және абсолют шамасы жағынан аз магнетиктер
диамагнетиктер деп аталады. Олар үшін <1.
Магнит сезімталдылығы æ 0 ( >1) және шама жағынан аз болатын
магнетиктер парамагнетиктер деп аталады.
Магнетиктердің тағы бір түрі – ферромагнетиктер, олар үшін æ 0 және
>>1 өте үлкен мәнге ие бола алады.
Диамагнетиктер деп - сыртқы магнит өрісі болмаған жағдайда атомдары мен
молекулаларының магнит моменттері нөлге тең заттарды айтады. Сыртқы
магнит өрісі болмаған кезде атомдардың магнит моменттері нөлге тең
болмаса парамагнетиктер деп аталады. Ферромагнетиктерге сыртқы магнит
өрісі жоқ болған кездің өзінде магниттелінуге ие болатын заттар жатады.
Ферромагнетиктің магниттік қасиеттері жоғалатын температура Кюри
температурасы деп аталады.
24