Постоянный электрический ток

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной физики и химии
Физика
Постоянный электрический ток
Рогожина Татьяна Сергеевна к.ф.-м.н., доцент
Дронов Владимир Михайлович к.ф.-м.н., доцент
Кирк Яна Геннадьевна к.п.н., доцент
Шабалин Владимир Владимирович д.б.н.,
Барашев Матвей Нестерович к.т.н.,

2.

2
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Понятия и определения
Электрический ток, сила и плотность тока
Закон Ома для однородного участка цепи. Сопротивление и проводимость проводника.
Зависимость сопротивления проводника от температуры. Сверхпроводимость. Закон Ома
в дифференциальной форме. Работа и мощность тока. Закон Джоуля – Ленца. Тепловое
действие тока. Сторонние силы. Напряжение и электродвижущая сила (ЭДС). Закон Ома
для неоднородного участка цепи в интегральной и дифференциальной форме
(обобщенный закон Ома). Цепи с источником тока. Разветвленные цепи, правила
Кирхгофа.
Вывод основных законов электрического тока в классической теории электропроводности
металлов

3.

3
1.Понятия и определения
Электрическим током называют упорядоченное движение зарядов.
При этом различают ток проводимости и конвекционный ток.
Ток проводимости представляет движение зарядов в проводниках, а конвекционный можно
рассматривать, как упорядоченное движение макроскопически заряженных тел.
Для возникновения и существования электрического тока необходимо:
1. наличие свободных носителей
упорядоченно,
2. наличие электрического поля
тока
—
заряженных
частиц,
способных
перемещаться
За направление тока условно принимают направление движения положительных зарядов.
В проводнике под действием приложенного электрического поля Е свободные электрические заряды
перемещаются: положительные — по полю, отрицательные — против поля.

4.

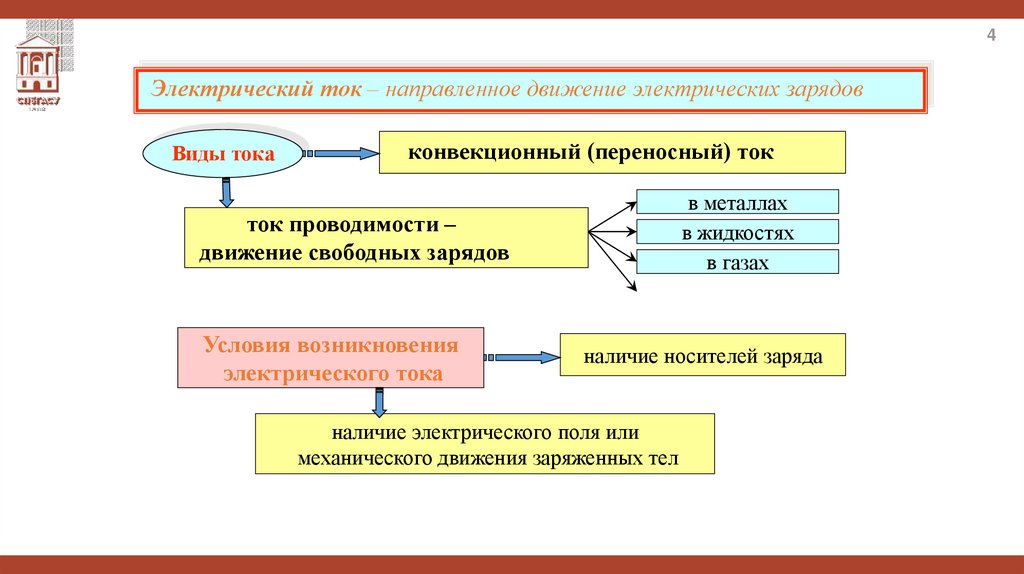
4
Электрический ток – направленное движение электрических зарядов
Виды тока
конвекционный (переносный) ток
в металлах
в жидкостях
в газах
ток проводимости –
движение свободных зарядов
Условия возникновения
электрического тока
наличие носителей заряда
наличие электрического поля или
механического движения заряженных тел

5.

5
2. Электрический ток, сила и плотность тока
Сила тока – скалярная величина, численно равная заряду, проходящему
через поперечное сечение проводника в единицу времени
dq
I
dt
1 Ампер = 1А=1 Кл/c
Единица измерения силы тока
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным
q
I
t
t2
Тогда следует, что
q Idt
t1
Если ток постоянный
q I t

6.

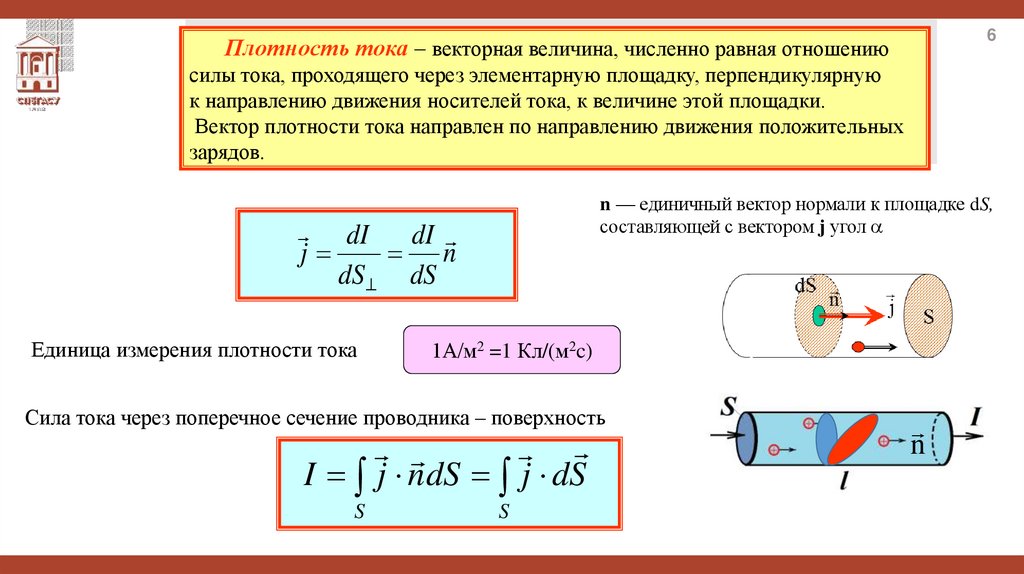
6
Плотность тока – векторная величина, численно равная отношению
силы тока, проходящего через элементарную площадку, перпендикулярную
к направлению движения носителей тока, к величине этой площадки.
Вектор плотности тока направлен по направлению движения положительных
зарядов.
n — единичный вектор нормали к площадке dS,
составляющей с вектором j угол
dI
dI
j
n
dS dS
Единица измерения плотности тока
1А/м2 =1 Кл/(м2c)
Сила тока через поперечное сечение проводника – поверхность
I j n dS j dS
S
S
n

7.

Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е (что не
обязательно для ионов), то за время dt через поперечное сечение S проводника переносится заряд
dQ=ne v S dt. Сила тока
I
n e v Sdt
n e v S
dt
плотность тока
7
I
j e n v
S
Анализ показывает, что для металлов средняя скорость упорядоченного движения свободных электронов
весьма мала и составляет величину порядка 10-3 м/с. Эта скорость называется скоростью дрейфа. Она
складывается со скоростью хаотического теплового движения, среднее значение модуля которой
значительно выше – при комнатной температуре оно равно 1,1·105 м/с. Однако вследствие хаотичности
среднее значение вектора скорости теплового движения равно нулю и поэтому это движение не может
привести к возникновению тока.
Комментарий 1. Если плотность тока во всех точках сечения одинакова, то сила тока
I jS const
Коментарий 2. В проводнике переменного сечения для сечений S1 и S2
j1S1 j2 S 2
- уравнение непрерывности тока (следствие закона сохранения заряда)

8.

3. Закон Ома для однородного участка цепи. Сопротивление и проводимость проводника
8
В 1826 году нем.физик Г.Ом экспериментально установил следующий закон, носящий его
имя: сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику,
в котором не действуют сторонние силы), пропорциональна напряжению U на концах
проводника
Закон Ома: сила тока в проводнике прямо пропорциональна приложенному напряжению и
обратно пропорциональна сопротивлению проводника
Г. Ом
(1787-1854)
U12 1 2
I
R
R
или
I GU 12
Коэффициент пропорциональности G называется Величина R называется электрическим сопротивлением
проводника.
электрической проводимостью проводника.
Единица измерения См (Сименс)
Единица измерения сопротивления – 1 Ом.

9.

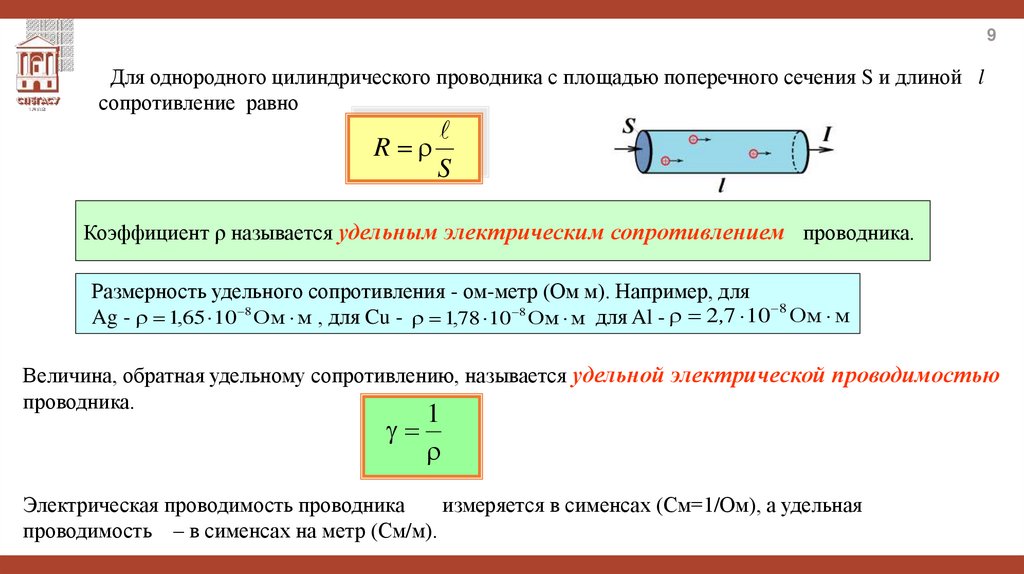
9
Для однородного цилиндрического проводника с площадью поперечного сечения S и длиной l
сопротивление равно
R
S
Коэффициент ρ называется удельным электрическим сопротивлением проводника.
Размерность удельного сопротивления - ом-метр (Ом м). Например, для
8
Ag - 1,65 10 8 Ом м , для Cu - 1,78 10 8 Ом м для Al - 2 ,7 10 Ом м
Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью
проводника.
1
Электрическая проводимость проводника
измеряется в сименсах (См=1/Ом), а удельная
проводимость – в сименсах на метр (См/м).

10.

10
удельные электрические
сопротивления некоторых
материалов

11.

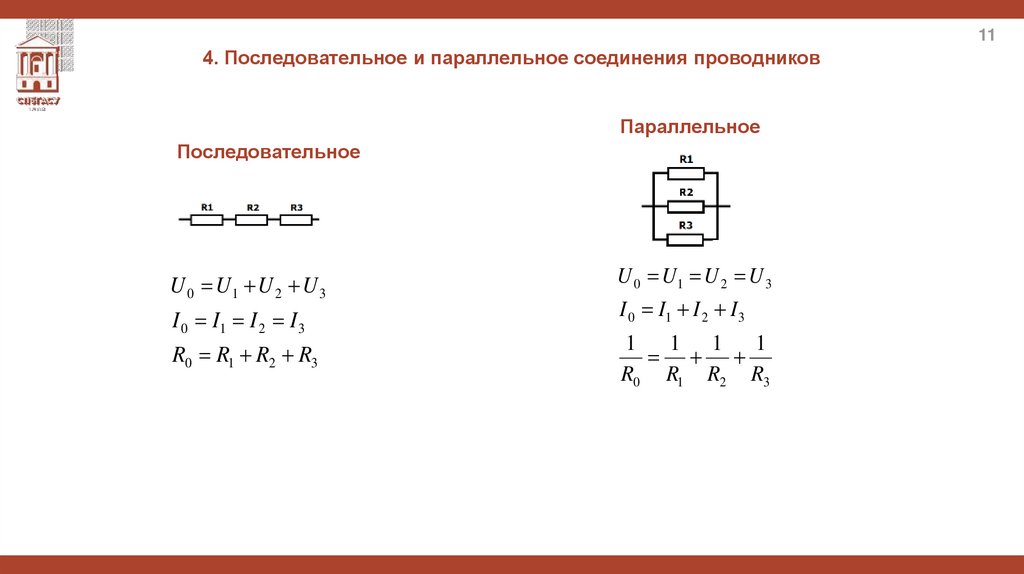
11
4. Последовательное и параллельное соединения проводников
Параллельное
Последовательное
U 0 U1 U 2 U 3
I 0 I1 I 2 I 3
R0 R1 R2 R3
U 0 U1 U 2 U 3
I 0 I1 I 2 I 3
1
1 1 1
R0 R1 R2 R3

12.

12
5. Зависимость сопротивления проводника от температуры.
Общая характеристика явления сверхпроводимости
Сопротивление вещества в общем случае зависит от температуры сложным образом.
Однако для многих проводников эта зависимость имеет простой вид:
R R 0 (1 t )
где t - температура проводника по Цельсию, R 0 - сопротивление проводника
при t 0o C , - температурный коэффициент сопротивления.
Для всех чистых металлов температурный коэффициент сопротивления примерно
равен 1/ 273 0,00367 . В этом случае зависимость может быть представлена
в виде:
R R 0 T
R
где T - термодинамическая температура.
T
0K Tкр
Рис.3

13.

Г.Камерлинг-Оннес
(1853-1926)
Ноб.пр. 1913
13
Это открытие было сделано в 1911 году нидерландским физиком Г.Камерлинг Оннесом , который обнаружил, что для большой группы металлов (Hg, Al, Pb, Zn и
ряда др), а также их сплавов при очень низких температурах (0,1 – 20 К), называемых
критическими, сопротивление вещества скачком уменьшается до нуля.
Это явление получило название сверхпроводимости Отметим, что в настоящее
время получены сверхпроводники с Tкр≈100 К.
•Явление сверхпроводимости объясняется на основе квантовой теории. Практическое
использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов,
в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур.
•На зависимости электрического сопротивления металлов от температуры основано
действие термометров сопротивления, которые позволяют по градуированной
взаимосвязи сопротивления от температуры измерять температуру с точностью до
0,003 К. Термометры сопротивления, в которых в качестве рабочего вещества
используются полупроводники, изготовленные по специальной технологии,
называются термисторами. Они позволяют измерять температуры с точностью до
миллионных долей кельвин.

14.

14
6. Закон Ома в дифференциальной форме
Ограничимся случаем изотропного проводника, в котором направления векторов j и Е совпадают.
Выделим мысленно в окрестности некоторой точки проводящей среды элементарный цилиндрический
объем с образующими, параллельными вектору j, а значит, и вектору Е. Если поперечное сечение цилиндра
dS, а его длина dl, то можно записать для такого элементарного цилиндра
dU
Ed
1
dI jdS
EdS
R ( d / dS )
откуда следует, что плотность тока линейно зависит от напряженности электростатического поля в проводнике:
1
j E E
В любой точке проводника вектор плотности тока направлен по вектору напряженности
электрического поля и по величине равен произведению напряженности поля на удельную
проводимость проводника в этой точке

15.

15
Под действием электростатического поля в проводнике возникает упорядоченное
движение зарядов, при этом установлено, что скорость дрейфа линейно зависит от
напряженности поля:
v E
Коэффициент μ называется подвижностью зарядов. Он имеет размерность м 2 / В с
3
2
(например, для электронов в Cu 3,2 10 3 м 2 / В с, в Ag 1,7 10 м / В с)
Из формул
j E
может быть получена удельная проводимость
j e n v
en

16.

16
7. Работа и мощность тока. Закон Джоуля - Ленца
Продолжим рассмотрение однородного и изотропного цилиндрического проводника,
к концам которого приложено постоянное напряжение
U U12 1 2
В этом случае за время dt через поперечное сечение проводника переносится заряд
dq Idt
и при этом совершается элементарная работа
A dq( 1 2 ) UIdt
Используя закон Ома в виде, представим эту работу в виде:
2
U
A UIdt I 2 Rdt
dt
R
Соответствующая мощность тока равна
2
A
U
P
UI I 2 R
dt
R

17.

Тепловое действие тока. Закон Джоуля - Ленца
17
Если проводник неподвижен, то, в соответствии с законом сохранения
энергии, вся работа по перемещению зарядов идет на его нагревание:
2
U
Q A I 2Rdt
dt
R
Этот закон теплового действия тока был экспериментально
открыт независимо друг от друга Джоулем и Ленцем и получил
название закона Джоуля-Ленца.
Д. Джоуль
(1818-1889)
Закон Джоуля – Ленца в дифференциальной форме
Рассмотрим неподвижный бесконечно малый элементарный объём
проводника с плотностью тока j, в виде цилиндрика, ограниченный
образующими, с поперечным сечением dS и длиной dl. Тогда количество
теплоты, выделившееся на этом участке за время dt
d
Q I Rdt ( jdS ) dt j 2 dVdt
dS
2
2
Э. Ленц
(1804-1865)

18.

Количество теплоты, выделяющееся за единицу времени в единице объема,
называется удельной тепловой мощностью тока.
18
Q
P
w j 2
dtdV dV
Для однородных и изотропных проводников, с учетом закона Ома в локальной форме j=γE получим
w j 2 jE E 2
Удельная тепловая мощность тока в любой точке
проводника равна произведению удельного сопротивления
на квадрат плотости тока в этой точке
А.Н.Лодыгин
(1847-1923)
Формула называется законом Джоуля-Ленца в дифференциальной форме.
Практическое значение и применение эффекта нагревания проводников электрическим
током. Лампы накаливания (А.Н.Лодыгин, создатель лампы накаливания – 1872 год, ему
принадлежит приоритет в применении вольфрама для нити накала).

19.

8. Сторонние силы. Напряжение и электродвижущая сила (ЭДС)
19
Для поддержания постоянного тока в цепи необходимо, чтобы на носители тока действовали не
только электростатические (кулоновские) силы, но также и другие, неэлектростатические силы.
Эти силы называются сторонними силами, а устройства, их создающие, - источниками
тока (гальванические элементы, генераторы и т.п.)
При перемещении заряда q между точками 1 и 2 проводника совершается
работа, которая в общем случае складывается из работы как кулоновских, так
и и сторонних сил:
A12 A12 кул A12 ст
Для характеристики работы сторонних сил на участке 1–2 вводится специальная физическая величина,
равная отношению работы этих сил к величине перемещаемого заряда:
Aст 1 2
Fст d
q
q1
Эта величина называется электродвижущей силой сокращенно ЭДС),
действующей на участке 1–2. ЭДС, как и напряжение, измеряется в вольтах.

20.

20
Aкул q Ed q( 1 2 )
Работа кулоновских сил на участке 1–2 равна
1
2
2
Работа сторонних сил по перемещению заряда q на участке цепи равна Aст Fст d q Eст d q
2
Тогда
A12 q 12 q( 1 2 )
1
1
Напряжением U на участке 1—2 называется физическая величина, определяемая работой, совершаемой суммарным
полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на
данном участке цепи. Таким образом
U12
A12
q
U12 ( 1 2 ) 12
Таким образом, понятие напряжения обобщает понятие обобщает понятие разности потенциалов: напряжение
на участке 1 – 2 совпадает с разностью потенциалов только в том случае, когда на участке 1 – 2 сторонние силы не
действуют. В этом случае участок цепи называется однородным, если на участке действуют
сторонние силы, то он называется неоднородным. Если цепь является замкнутой (точки 1 и 2 совпадают), то работа по
перемещению заряда равна
A qEd Fст d Fст d A ст q
так как электростатическое поле потенциально и первый интеграл в равен нулю. Это означает, что всю
работу по перемещению зарядов в замкнутой цепи осуществляют сторонние силы.

21.

9. Закон Ома для неоднородного участка цепи в интегральной
форме (обобщенный закон Ома)
21
Теперь рассмотрим неоднородный участок цепи, где действующую э.д.с. на участке 1—2 обозначим через ε12, а приложенную
на концах участка разность потенциалов — через 1 — 2.
Если ток проходит по неподвижным проводникам, образующим участок 1—2, то работа А12 всех сил (сторонних и
электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте,
выделяющейся на участке. Работа сил, совершаемая при перемещении заряда q на участке 1—2, согласно,
A12 q 12 q( 1 2 )
Если э.д.с. способствует движению положительных зарядов в выбранном направлении (в направлении 1—2), то ε12> 0.
Если э.д.с. препятствует движению положительных зарядов в данном направлении, то ε12< 0. За время t в проводнике
выделяется теплота
2
Q I Rt IR( It ) IRq
Из формул получим
IR ( 1 2 ) 12
( 1 2 ) 12
I
R
Сила тока на произвольном участке цепи равна отношению напряжения между его
начальной и конечной точками, к сопротивлению этого участка:
Выражение представляет собой закон Ома для неоднородного участка цепи в
интегральной форме, который является обобщенным законом Ома.

22.

22
Если на данном участке цепи источник тока отсутствует (ε12=0), то приходим к закону Ома для
однородного участка цепи:
I
( 1 2 ) U
R
R
при отсутствии сторонних сил напряжение на концах участка равно разности потенциалов. Если же электрическая цепь
замкнута, то выбранные точки 1 и 2 совпадают, 1= 2; тогда получаем закон Ома для замкнутой цепи:
I
R
где ε- э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае R=r+R1, где r —
внутреннее сопротивление источника тока, R1—сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи
будет иметь вид:
I
R r
Если цепь разомкнута и, следовательно, в ней ток отсутствует (I = 0), то из закона Ома получим, что ε12= 1— 2, т. е.
э.д.с., действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Следовательно, для того чтобы
найти э.д.с. источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

23.

10. Закон Ома для неоднородного участка цепи в дифференциальной
форме (обобщенный закон Ома)
23
2
Из обобщённого закона Ома
IR12 1 2 Eст d
1
для любого элементарного участка цепи dl
или
d
I
IdR d Eст d
S
I
d
( E ст )
S
d
Считая проводник однородным и изотропным, его площадь поперечного сечения проводника постоянной, а
напряженности полей и плотность тока – перпендикулярными этому сечению, закон можно записать в скалярном виде:
j ( E Eст )
которое представляет собой обобщенный закон Ома в дифференциальной форме.

24.

11. Цепи с источником тока
закон Ома для замкнутой цепи
24
I
R r
Напряжение на внешнем сопротивлении или источнике цепи
U Ir
Падение напряжения на внутреннем сопротивлении источника
U r Ir
Мощность во внешней цепи и коэффициент полезного действия источника тока
P UI I I 2 r
2
P I R
R
2
(R r)
2
2
P I R
R
2
(R r)
2
2 (( R r ) 2 R 2 ( R r ))
P' 0
R r
(R r)4
КПД цепи
Qполез Pполезt UI U
IR
R
Qзатр Pзатр t I I ( R r ) ( R r )
2
2
Pmax
r
4r
( r r )2

25.

12. Разветвлённые цепи. Правила Кирхгофа
Расчет разветвленных цепей, например, нахождение токов в отдельных ее ветвях, значительно упрощается, если
пользоваться двумя правилами Кирхгофа.
Узел – точка где сходится три и более проводов
Ветвь – участок цепи от узла до узла
Контур – замкнутый участок цепи
Первое правило Кирхгофа — оно относится к узлам цепи, т. е. к точкам ее разветвления:
алгебраическая сумма токов, сходящихся в узле, равна нулю
Ii 0
1 Правило Кирхгофа
I1 I 2 I 3 I 4 I 5 0
Второе правило Кирхгофа — оно относится к любому выделенному в разветвленной цепи замкнутому контуру:
алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивления
равна алгебраической сумме э.д.с, действующих в этом контуре
I1 I 2 I 3 0
I i Ri i
2 Правило Кирхгофа
I1R1 I 2 R2 2
I1R1 I 3 R3 1
25

26.

Разветвлённые цепи. Правила Кирхгофа
Рассмотрим случай, когда выделенный контур состоит из трех участков. Зададим направление
обхода, например, по часовой стрелке, как показано на рисунке. Затем применим к каждому из
трех участков закон Ома:
I1R1 2 3 1
I 2 R2 3 1 2
I 3 R3 1 2 3
Сложив эти равенства, приходим после сокращения всех потенциалов к формуле, т. е. ко второму правилу
Кирхгофа. Таким образом, уравнение является следствием закона Ома для неоднородных участков цепи.
Используя два правила Кирхгофа можно рассчитать все токи.
26

27.

Разветвлённые цепи. Правила Кирхгофа
27
Используя два правила Кирхгофа можно рассчитать все токи.
Алгоритм составления уравнений по правилам Кирхгофа.
1.Рассмотрим исследуемую цепь и находим все узлы. Произвольным образом расставляем
направление токов от узла до узла.
2.Записываем первое правило Кирхгофа для N-1 узла. Для узла А
I1 I 2 I 3 0
3.Выбираем контуры. (Контуром является любой замкнутый участок сложной цепи.)
Выбираем в каждом контуре произвольно направление обхода.
4.Записываем столько уравнений по 2 правилу Кирхгофа, чтобы общее число уравнений
было равно числу неизвестных.
Правило знаков для 2 правила Кирхгофа.
I1R1 I 2 R2 2
I 3 R3 I 2 R2 2 1
1. Если направление тока совпадает с направлением обхода, то +IR, иначе –IR
2. Если э.д.с. создает ток в направлении обхода (включен положительно, повышает потенциал),
то +ε, иначе –ε.

28.

13. Вывод основных законов электрического тока в классической теории
электропроводности металлов
28
Закон Ома.
Co стороны поля заряд е испытывает действие силы F = eE и приобретает ускорение a=F/m=eE/m.
скорость
vmax eE t / m
t — среднее время между двумя последовательными соударениями электрона с ионами решетки
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в
поле энергию, поэтому скорость его упорядоченного движения становится равной нулю
v 0 eE t
l eE l
v max
t
2
2m
u 2m u
Плотность тока в металлическом проводнике
удельная проводимость материала
ne 2 l
j ne v
E
2m u
ne2 l
2m u
но закон Ома в
дифференциальной форме
j E

29.

Вывод основных законов электрического тока в классической теории
электропроводности металлов
29
Закон Джоуля — Ленца
К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию.
2
mvmax
e2 l 2 2
Eк
E
2
2
2m u
При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней
энергии металла, т. е. на его нагревание. За единицу времени электрон испытывает с узлами решетки в среднем z
u
столкновений:
z
l
Если n — концентрация электронов, то в единицу времени
происходит п z столкновений и решетке передается энергия
тогда
w n z Eк
w E 2
u e 2 l 2 2 ne 2 l 2
w n
E
E
2
l 2m u
2m u
удельная проводимость материала
но закон Джоуля-Ленца в
дифференциальной форме
ne2 l
2m u

30.

Санкт-Петербургский государственный
архитектурно-строительный университет
Кафедра строительной физики и химии
Авторы:
Рогожина Татьяна Сергеевна к.ф.-м.н., доцент
Дронов Владимир Михайлович к.ф.-м.н., доцент
Кирк Яна Геннадьевна к.п.н., доцент
Шабалин Владимир Владимирович д.б.н.,
Барашев Матвей Нестерович к.т.н.,
vladi-dronov@mail.ru