Похожие презентации:
Постоянный электрический ток
1. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
2. Причины электрического тока
•Заряженные объекты являются причиной не толькоэлектростатического поля, но еще и электрического тока.
В этих двух явлениях, есть существенное отличие:
•Для возникновения электростатического поля требуются
неподвижные, каким-то образом зафиксированные в
пространстве заряды.
• Для возникновения электрического тока, требуется
наличие свободных, не закрепленных заряженных частиц,
которые в электростатическом поле неподвижных зарядов
приходят в состояние упорядоченного движения вдоль
силовых линий поля.
•Упорядоченное движение свободных зарядов вдоль
силовых линий поля - электрический ток.
3.
Распределение напряженности Е и потенциала φэлектростатического поля связано с плотностью
распределения зарядов
в пространстве
уравнением Пуассона:
1
E
И
Где
1
Δφ ρ,
ε
q
ρ - объемная плотность заряда.
V
4.
Если заряды неподвижны, то есть
распределение зарядов в
пространстве стационарно, то ρ не
зависит от времени, в результате чего
и Е, и φ являются функциями только
координат, но не времени. Поэтому
поле и называется
электростатическим.
5.
• Наличие свободных зарядов приводитк тому, что становится функцией
времени, что, порождает изменение
со временем и характеристик
электрического поля, появляется
электрический ток. Поле перестает
быть электростатическим.
6.
Количественной мерой тока служит силатока I - заряд, перенесенный через
поверхность S (или через поперечное сечение
проводника), в единицу времени, т.е.:
q
I
t
7.
• Если, однако, движение свободных зарядов таково, чтооно не приводит к перераспределению зарядов в
пространстве, то есть к изменению со временем
плотности зарядов ρ, то в этом частном случае
электрическое поле – снова статическое.
• Этот частный случай есть случай постоянного тока.
Ток, не изменяющийся по величине со временем –
называется постоянным током
q
I
t
- Отсюда видна размерность силы тока в СИ:
Кл
1A ;
с
8. Плотность тока
•Есть две основные характеристики электрическоготока – это сила тока I и плотность тока j .
•В отличие от силы тока, которая есть величина
скалярная и направления не имеет, плотность тока –
это вектор.
•Связь между этими двумя физическими величинами
такова:
I j S
s
9.
Или наоборот, модуль вектора плотности токачисленно равен отношению силы тока через
элементарную площадку, перпендикулярную
направлению движения носителей заряда, к ее
площади:
I
j
S
10.
• Плотность тока j - есть более подробнаяхарактеристика тока, чем сила тока I.
• j - характеризует ток локально, в каждой
точке пространства,
• а I – это интегральная характеристика,
привязанная не к точке, а к области
пространства, в которой протекает ток.
11.
•Плотность тока j связана с плотностьюсвободных зарядов ρ и со скоростью их движения
:
v
j ρv др.
12.
За направление
вектора j принимают направление
вектора v положительных носителей зарядов
• Если носителями являются как положительные, так и
отрицательные заряды, то плотность тока
определяется формулой:
где
j q n v др. q n v др.
q n и q n – объемные плотности зарядов.
13.
• Там, где носители только электроны,плотность тока определяется
выражением:
j env др.
14.
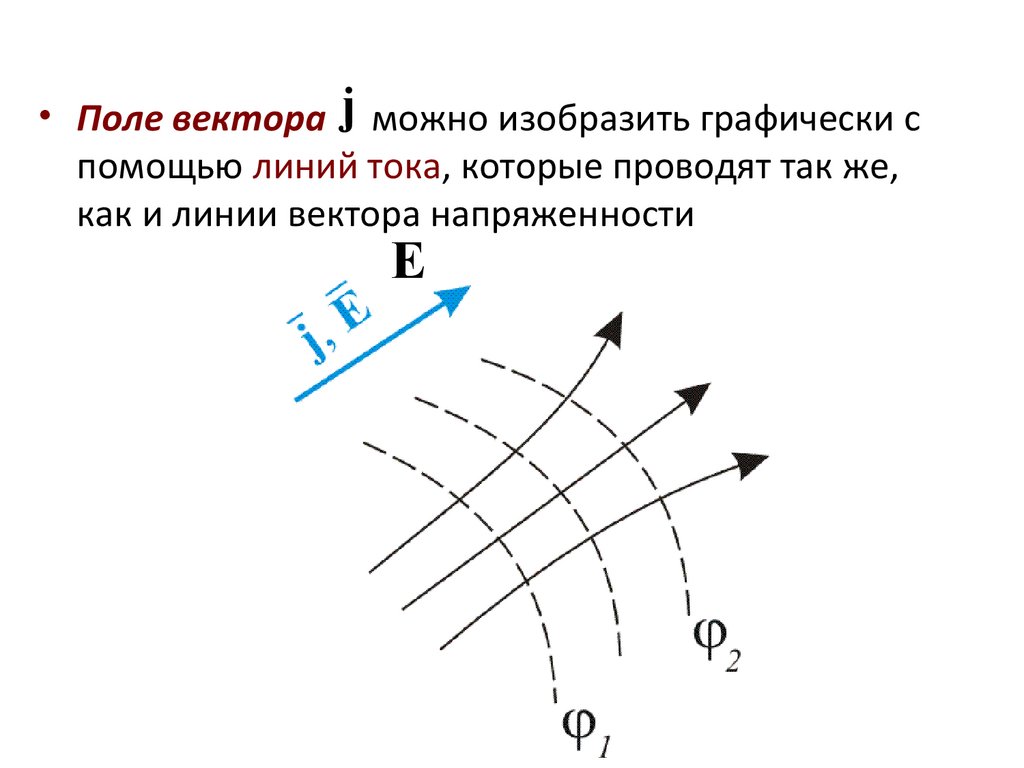
Поле вектора j можно изобразить графически с
помощью линий тока, которые проводят так же,
как и линии вектора
напряженности
E
15.
Зная j в каждой точке интересующей нас
поверхности S можно найти силу тока через
эту поверхность,
как поток вектора :
j
I j S.
S
16.
•Сила тока является скалярной величиной иалгебраической.
•А знак определяется кроме всего прочего,
выбором направления нормали к поверхности
S.
17. Уравнение непрерывности
• Представим себе, в некоторой проводящей среде,где течет ток, замкнутую поверхность S
• Для замкнутых поверхностей
векторы нормалей, а
следовательно, и векторы S принято брать наружу,
поэтому интеграл
j
S
S
дает заряд, выходящий в единицу времени
наружу из объема V, охваченного поверхностью
S.
18.
• Плотность постоянного электрическоготока одинакова по всему поперечному
сечению S однородного проводника.
• Поэтому для постоянного тока в
однородном проводнике с поперечным
сечением S сила тока:
I jS
19.
• Из этого следует, что плотностипостоянного тока в различных
поперечных сечениях 1 и 2 цепи обратно
пропорциональны площадям S1 и S2 этих
сечений :
j2 / j1 S1 / S 2
20.
• ПустьS
–
замкнутая
поверхность,
а
векторы
Sвсюду проведены по внешним нормалям n
• Тогда поток вектора j сквозь эту поверхность S
равен электрическому току I, идущему вовне из
области, ограниченный замкнутой поверхностью
S. Следовательно, согласно закону сохранения
электрического заряда, суммарный
электрический заряд q, охватываемый
поверхностью S, изменяется за время t на
q I t , тогда в интегральной форме можно
записать:
q
j S .
S
t
21.
• В интегральной форме можно записать:q
j S t
S
• Это соотношение называется уравнением
непрерывности.
• Оно является, по существу, выражением закона
сохранения электрического заряда.
• Дифференциальная форма записи уравнения
непрерывности.
ρ
j
t
22.
• В случае постоянного тока, распределениезарядов в пространстве должно оставаться
неизменным:
q
0,
t
• следовательно,
j
S
0
,
• это уравнение непрерывности для
постоянного тока (в интегральной форме).
23.
jв случае постоянного тока• Линии
нигде не начинаются и нигде не
заканчиваются.
• Поле вектора
не имеет источника.
j
• В дифференциальной форме
уравнение непрерывности для
постоянного тока:
j 0
24.
• Если ток постоянный, то избыточный заряд внутриоднородного проводника всюду равен нулю.
• Докажем это: т.к. для постоянного тока справедливо
уравнение
отсюда
j S 0
S
qi 0.
• Избыточный заряд может появиться только на
поверхности проводника в местах соприкосновения с
другими проводниками, а также там, где проводник
имеет неоднородности.
25. Сторонние силы и ЭДС
• Для того, чтобы поддерживать токдостаточно длительное время, необходимо
от конца проводника с меньшим
потенциалом непрерывно отводить, а к
другому концу – с большим потенциалом –
подводить электрические заряды.
• Т.е. необходим круговорот зарядов.
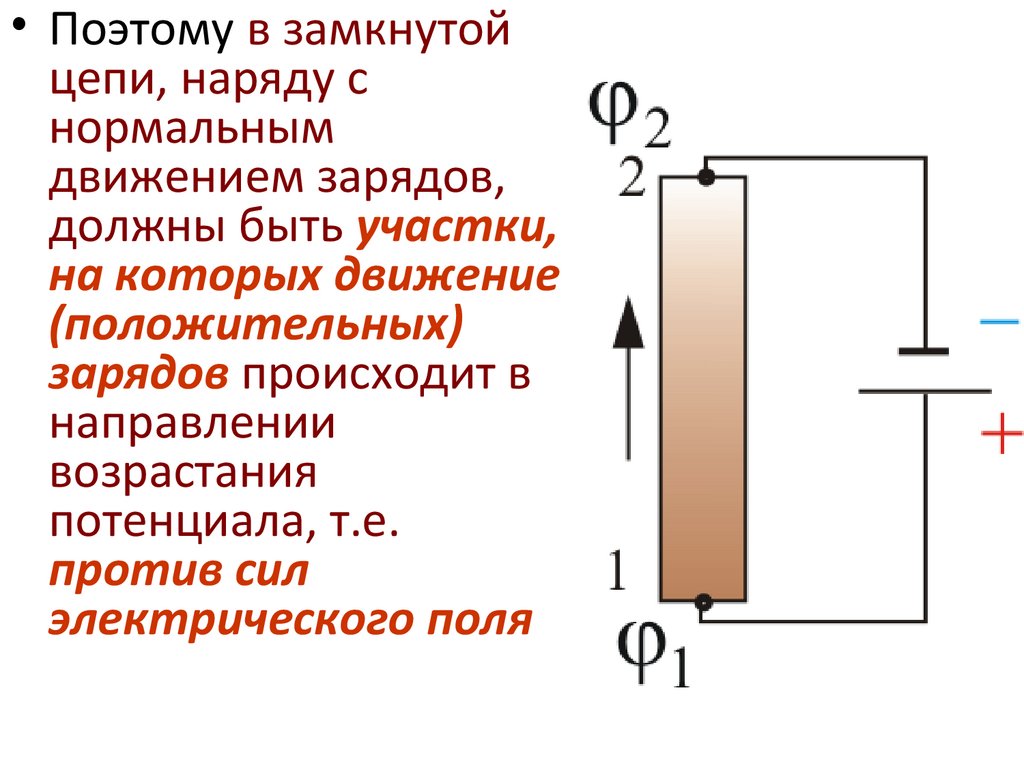
26.
• Поэтому в замкнутойцепи, наряду с
нормальным
движением зарядов,
должны быть участки,
на которых движение
(положительных)
зарядов происходит в
направлении
возрастания
потенциала, т.е.
против сил
электрического поля
27.
Перемещение заряда на этихучастках возможно лишь с
помощью сил
неэлектрического
происхождения (сторонних
сил): химические процессы,
диффузия носителей заряда,
вихревые электрические поля.
Аналогия: насос, качающий
воду в водонапорную башню,
действует за счет негравитационных сил (электромотор).
28.
• Сторонние силы можнохарактеризовать работой,
которую они совершают над
перемещающимися по
замкнутой цепи зарядами
29.
• Величина, равная работе сторонних силпо перемещению единичного
положительного заряда в цепи,
называется электродвижущей силой
(ЭДС), действующей в цепи:
A
E ;
q
Дж
В
Кл
30.
• Стороннюю силу, действующую назаряд, можно представить в виде:
Fст E ст q,
E ст – напряженность поля сторонних сил.
31.
• Работа сторонних сил на участке 1 – 2:2
2
A12 Fст d l q E ст d l ,
• Тогда ЭДС
1
1
2
A12
E12 E ст d l .
q 1
• Для замкнутой цепи:
E Ei E ст d l .
32.
E Ei E ст d l .• Циркуляция вектора напряженности сторонних сил
равна ЭДС, действующей в замкнутой цепи
(алгебраической сумме ЭДС).
• При этом необходимо помнить, что поле сторонних
сил не является потенциальным, и к нему нельзя
применять термин разность потенциалов или
напряжение.
33. Закон Ома для неоднородного участка цепи
Один из основных законов
электродинамики был открыт в 1826 г.
немецким учителем физики Георгом
Омом.
• Он установил, что сила тока в
проводнике пропорциональна разности
потенциалов:
φ1 φ 2
I
R
34.
• Георг Симон Ом (1787 – 1854) – немецкийфизик.
• В 1826 г. Ом открыл основной закон
электрической цепи. Этот закон не сразу
нашел признание в науке, а лишь после
того, как Э. X. Ленц, Б. С. Якоби, К. Гаусс,
Г. Кирхгоф и другие ученые положили его в
основу своих исследований.
• Именем Ома была названа единица
электрического сопротивления (Ом).
• Ом вел также исследования в области
акустики, оптики и кристаллооптики.
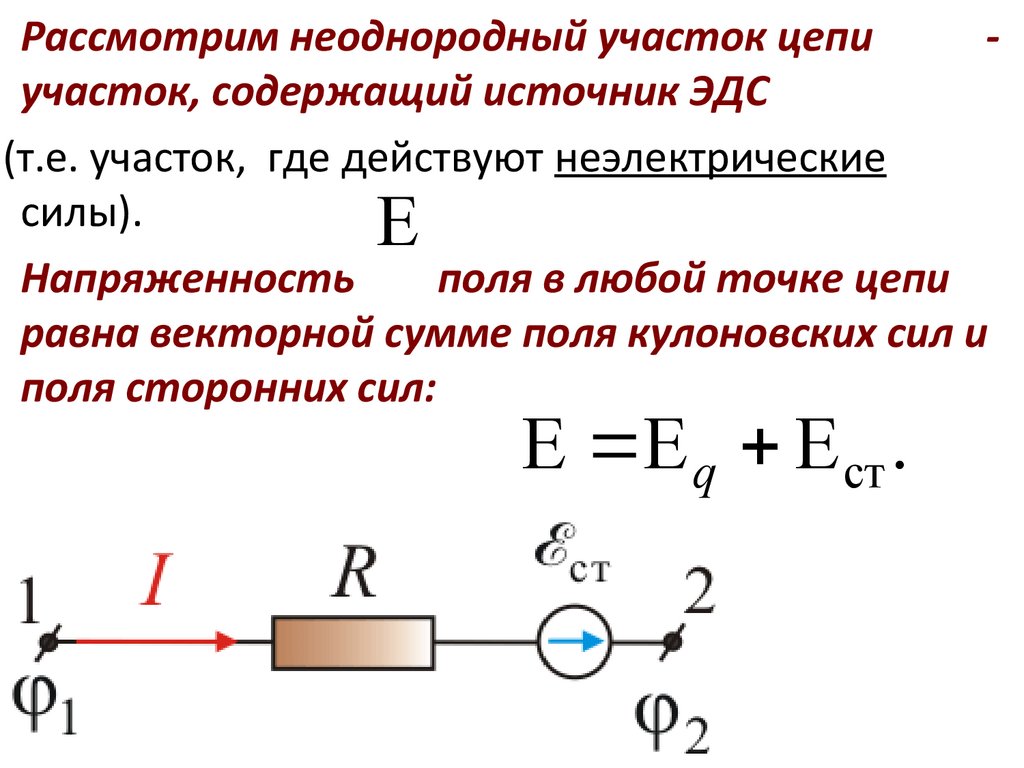
35.
Рассмотрим неоднородный участок цепиучасток, содержащий источник ЭДС
(т.е. участок, где действуют
неэлектрические
силы).
E
Напряженность
поля в любой точке цепи
равна векторной сумме поля кулоновских сил и
поля сторонних сил:
E E q E ст .
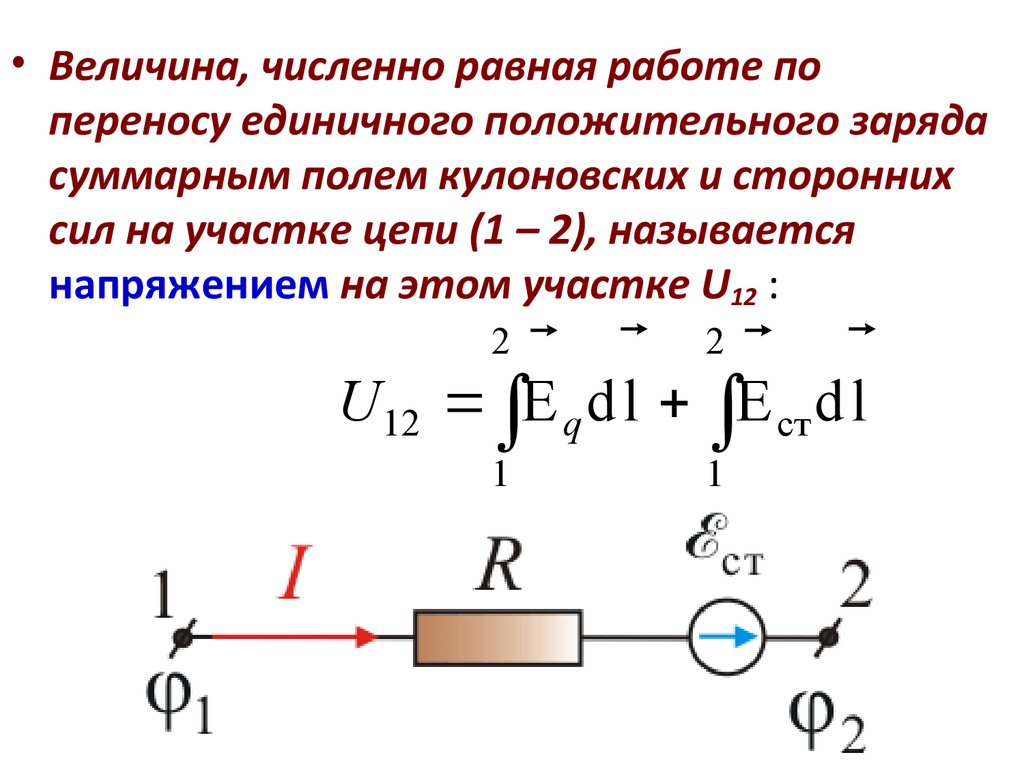
36.
• Величина, численно равная работе попереносу единичного положительного заряда
суммарным полем кулоновских и сторонних
сил на участке цепи (1 – 2), называется
напряжением на этом участке U12 :
2
U 12
2
E q d l E ст d l
1
1
37.
Т.к. E q d l dφ или2
E
d
l
φ
φ
q
1
2
1
тогда
U 12 (φ1 φ 2 ) E12 .
38.
U 12 (φ1 φ 2 ) E12 .• Напряжение на концах участка цепи совпадает с
разностью потенциалов только в случае, если на
этом участке нет ЭДС, т.е. на однородном
участке цепи.
• Обобщенный закон Ома для участка цепи
содержащей источник ЭДС:
IR12 (φ1 φ 2 ) E12 .
39.
• Обобщенный закон Ома выражает законсохранения энергии применительно к
участку цепи постоянного тока.
• Он в равной мере справедлив как для
пассивных участков (не содержащих
ЭДС), так и для активных.
40.
• В электротехнике часто используют терминпадение напряжения – изменение
напряжения вследствие переноса заряда
через сопротивление
U IR.
41.
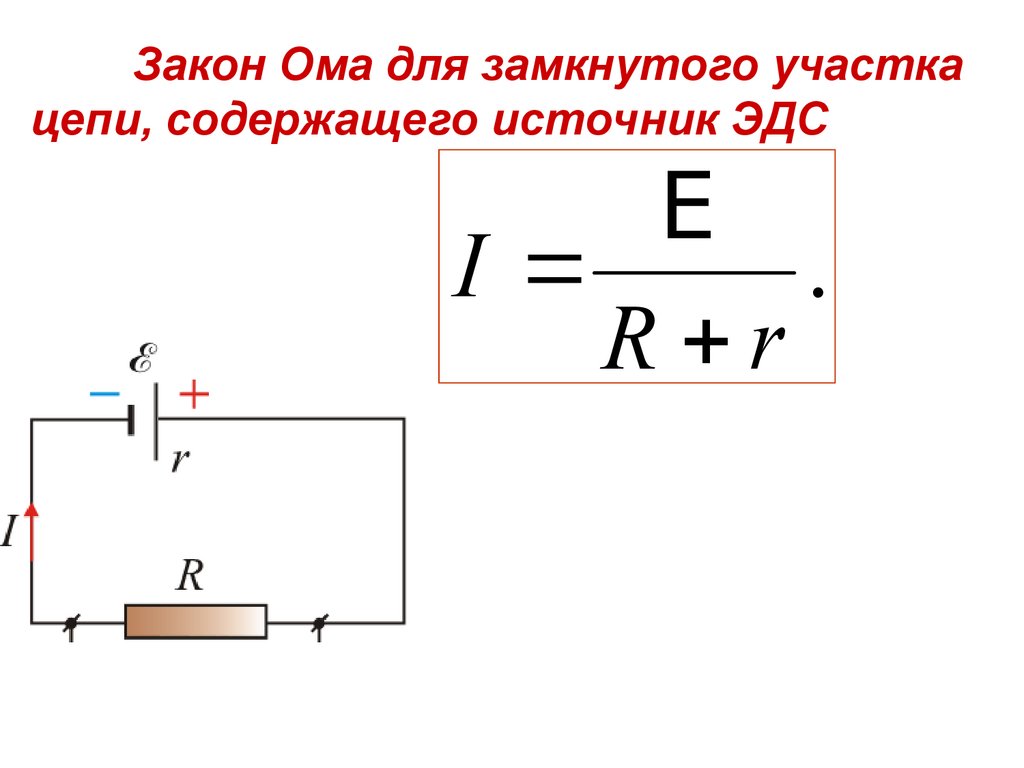
• В замкнутой цепи:E
• или
I ,
φ1 ;φ 2
IRΣ E
R
• где RΣ R ;r r – внутреннее сопротивление
активного участка цепи
• Тогда закон Ома для замкнутого участка цепи,
содержащего источник ЭДС запишется в виде
E
I
.
R r
42.
Закон Ома для замкнутого участкацепи, содержащего источник ЭДС
E
I
.
R r
43. Закон Ома в дифференциальной форме
• Закон Ома в интегральной форме дляоднородного участка цепи (не содержащего
ЭДС)
U
I
R
• Для однородного линейного проводника
выразим R через ρ:
l
R ρ
S
ρ – удельное объемное сопротивление;
• [ρ] = [Ом·м].
44.
• Найдем связь между j иE в бесконечномалом объеме проводника – закон Ома в
дифференциальной форме.
45.
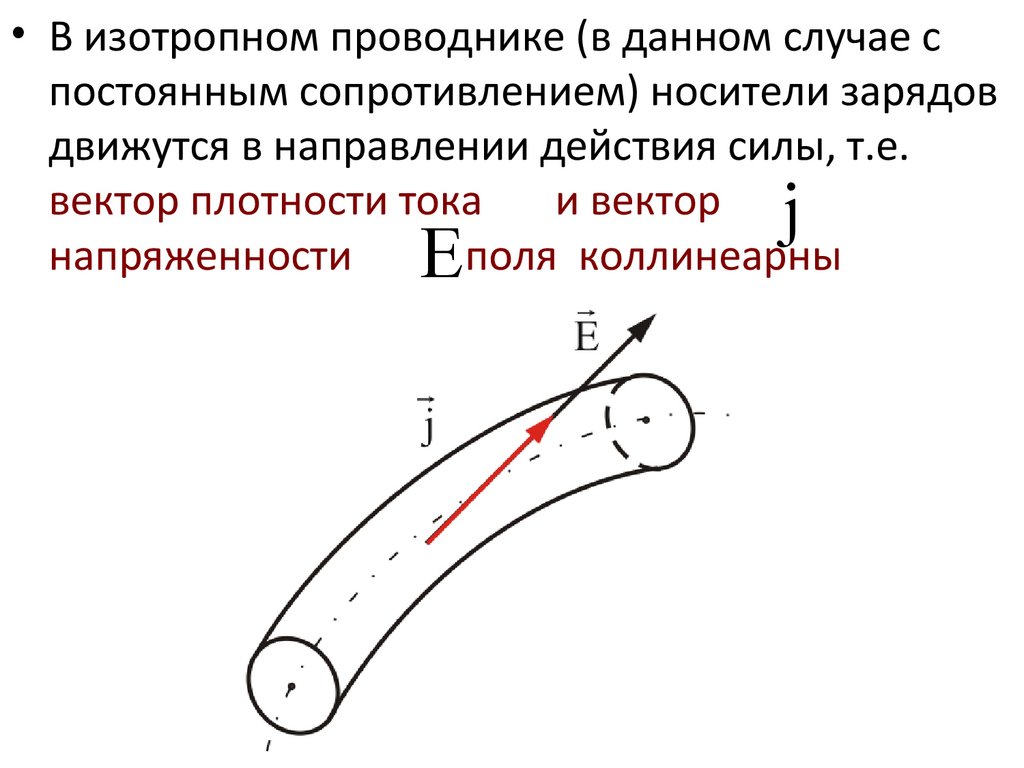
• В изотропном проводнике (в данном случае спостоянным сопротивлением) носители зарядов
движутся в направлении действия силы,
т.е.
вектор плотности тока
и вектор j
напряженности
поля коллинеарны
E
46.
• Исходя из закона Ома , имеем:U Edl EdS
I
R ρ dl
ρ
dS
d
I
1
• А мы знаем, что
j
dS ρ
• Отсюда
E
j σE
• это запись закона Ома в дифференциальной
форме.
σ 1 / ρ – удельная
• Здесь
электропроводность.
47.
• Плотность тока можно выразить через зарядэлектрона е, количество
зарядов
n
и
дрейфовую скорость υ :
j enυ
• Обозначим b υ , тогда
E
j enbE
υ bE
;
48.
• Теперь, если удельнуюэлектропроводность σ выразить через е, n
и b:
σ enb,
то вновь получим выражение закона Ома в
дифференциальной форме:
j σE
49. Работа и мощность тока. Закон Джоуля – Ленца
Рассмотрим произвольный участок цепи, к
концам которого приложено напряжение U. За
время dt через каждое сечение проводника
проходит заряд
dq Idt.
При этом силы электрического поля,
действующего на данном участке, совершают
dA Udq UIdt.
работу:
Общая работа:
A IUt
50.
• Разделив работу на время, получим выражение длямощности:
dA
N
dt
UI .
• Полезно вспомнить и другие формулы для мощности и
работы:
2
N RI ;
2
A RI t.
• В 1841 г. манчестерский пивовар Джеймс Джоуль и в
1843 г. петербургский академик Эмилий Ленц
установили закон теплового действия электрического
тока.
51.
• Джоуль Джеймс Пресскотт (1818 – 1889) –английский физик, один из первооткрывателей
закона сохранения энергии. Первые уроки по
физике ему давал Дж. Дальтон, под влиянием
которого Джоуль начал свои эксперименты.
Работы посвящены электромагнетизму,
кинетической теории газов.
• Ленц Эмилий Христианович (1804 – 1865) –
русский физик. Основные работы в области
электромагнетизма. В 1833 г. установил правило
определения электродвижущей силы индукции
(закон Ленца), а в 1842 г. (независимо от Дж.
Джоуля) – закон теплового действия
электрического тока (закон Джоуля-Ленца).
Открыл обратимость электрических машин. Изучал
зависимость сопротивление металлов от
температуры. Работы относятся также к геофизике.
52.
• При протекании тока, в проводникевыделяется количество теплоты:
2
Q RI t.
• Если ток изменяется со временем:
2
2
Q RI dt
1
• Это закон Джоуля – Ленца в интегральной
форме.
53.
• Отсюда видно, что нагревание происходит засчет работы, совершаемой силами поля над
зарядом.
• Соотношение имеет интегральный характер и
относится ко всему проводнику с сопротивлением
R, по которому течет ток I.
• Получим закон Джоуля-Ленца в локальнойдифференциальной форме, характеризуя
тепловыделение в произвольной точке.
54.
Тепловая мощность тока в элементепроводника Δl, сечением ΔS, объемом
ΔV Δl ΔS равна:
2
N I R I φ j SE l j E V
Тепловая мощность тока
N j E V
Удельная мощность тока
N
ω
jE
V
55.
• Согласно законув
дифференциальной
форме
Ома
j σE
• получим
закон Джоуля - Ленца в дифференциальной форме,
2
характеризующий плотность выделенной
энергии.
ω E
• Так как выделенная теплота равна работе сил
электрического поля
A IUt
• то мы можем записать для мощности тока:
N UI RI
2
56.
• Мощность, выделенная в единицеобъема проводника .
ω ρj
2
• Приведенные формулы справедливы для
однородного участка цепи и для
неоднородного.
57.
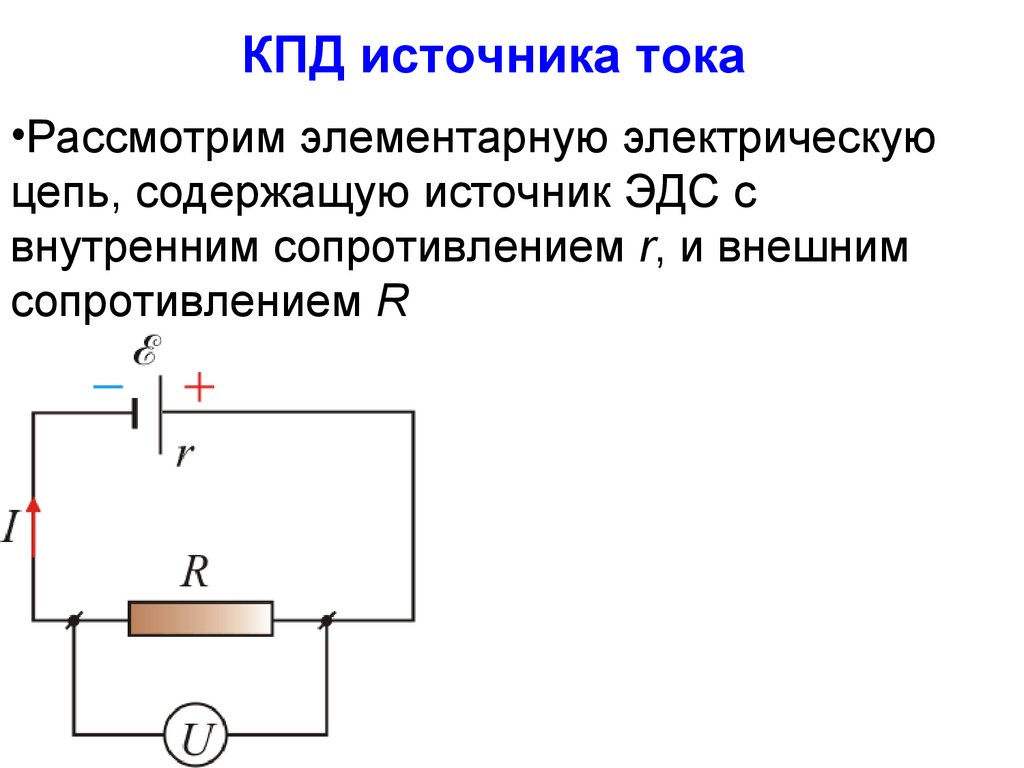
КПД источника тока•Рассмотрим элементарную электрическую
цепь, содержащую источник ЭДС с
внутренним сопротивлением r, и внешним
сопротивлением R
58.
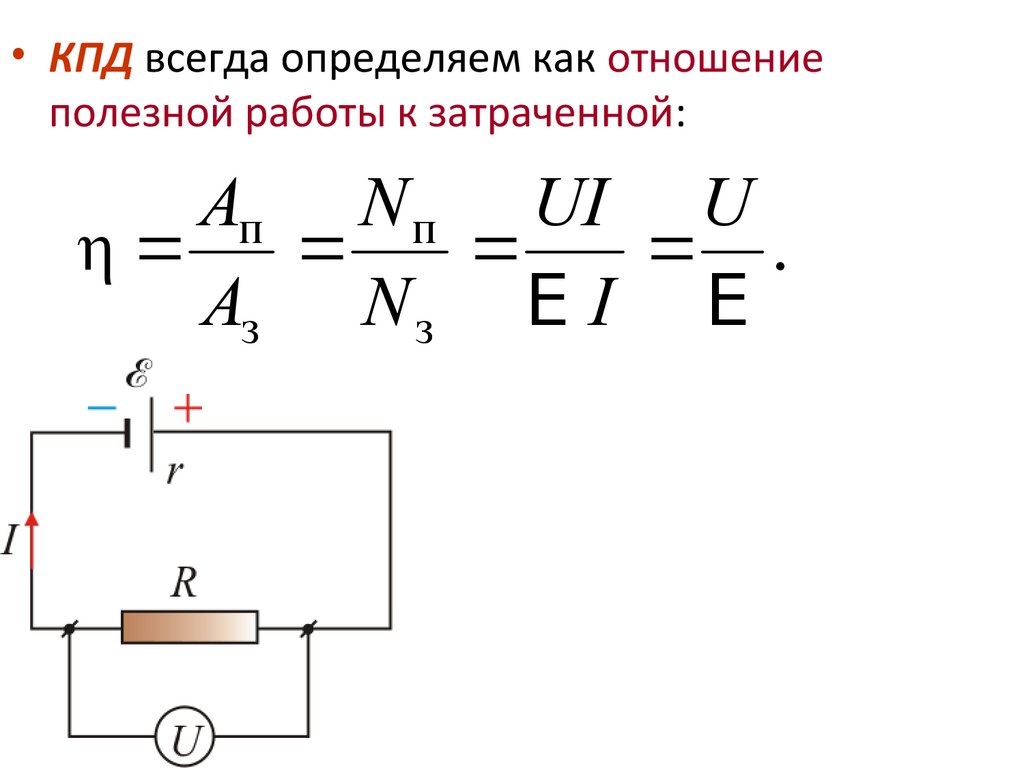
• КПД всегда определяем как отношениеполезной работы к затраченной:
Aп N п UI U
η
.
Aз N з E I E
59.
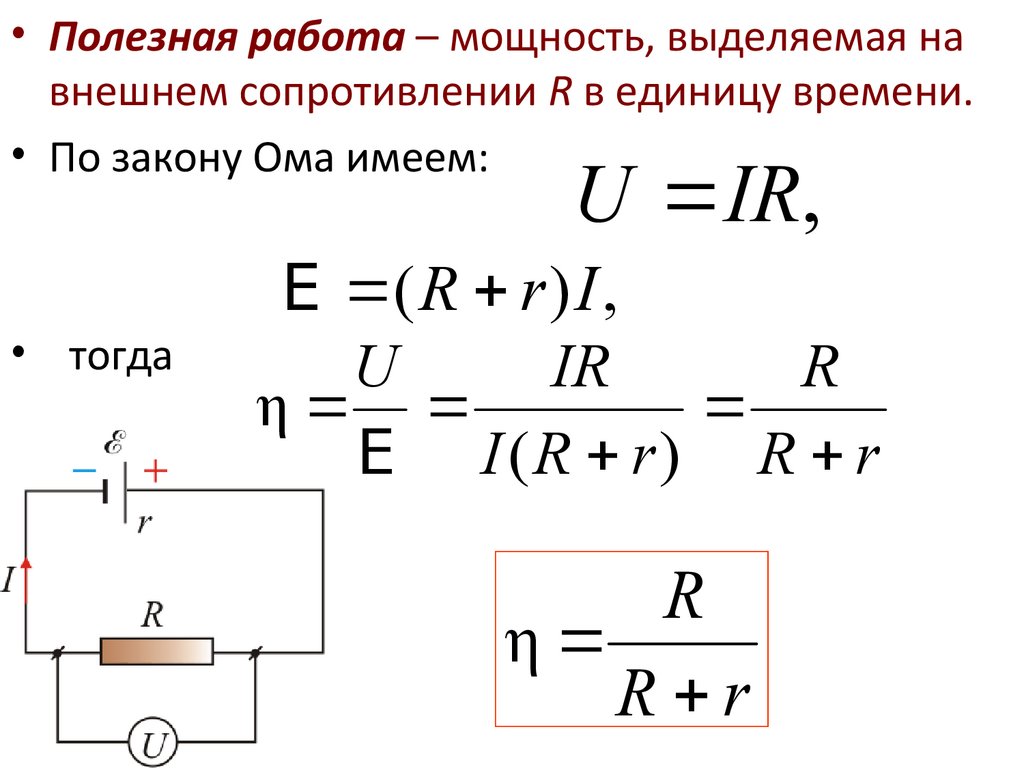
• Полезная работа – мощность, выделяемая навнешнем сопротивлении R в единицу времени.
• По закону Ома имеем:
U IR,
• тогда
E ( R r ) I ,
U
IR
R
η
E I (R r) R r
R
η
R r
60.
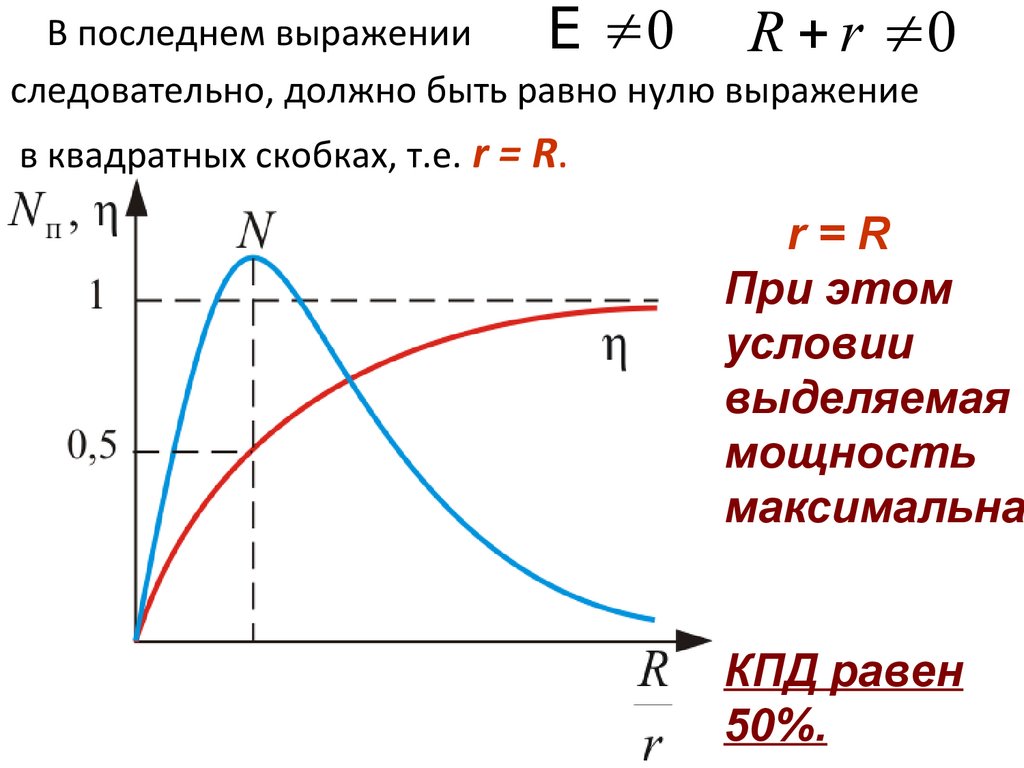
• Таким образом, имеем, что при R ,η 1, но при этом ток в цепи мал и полезная
мощность мала.
• Вот парадокс – мы всегда стремимся к
повышенному КПД, а в данном случае нам это
не приносит пользы.
Найдем условия, при которых
полезная мощность будет максимальна.
• Для этого нужно, чтобы
dN п
0.
dR
61.
22
E R
N
2
r R
E
N п I R
R
R r
2
2
2
2
dN п E R r 2 r R E R
0
4
dR
R r
E
2
R r
Это возможно при R = r
2 R 0
62.
В последнем выраженииE 0 R r 0
следовательно, должно быть равно нулю выражение
в квадратных скобках, т.е. r = R.
r=R
При этом
условии
выделяемая
мощность
максимальна
КПД равен
50%.
63. Правила Кирхгофа для разветвленных цепей
• Расчет разветвленных цепей с помощьюзакона Ома довольно сложен.
• Эта задача решается более просто с
помощью двух правил немецкого физика Г.
Кирхгофа (1824 – 1887).
64.
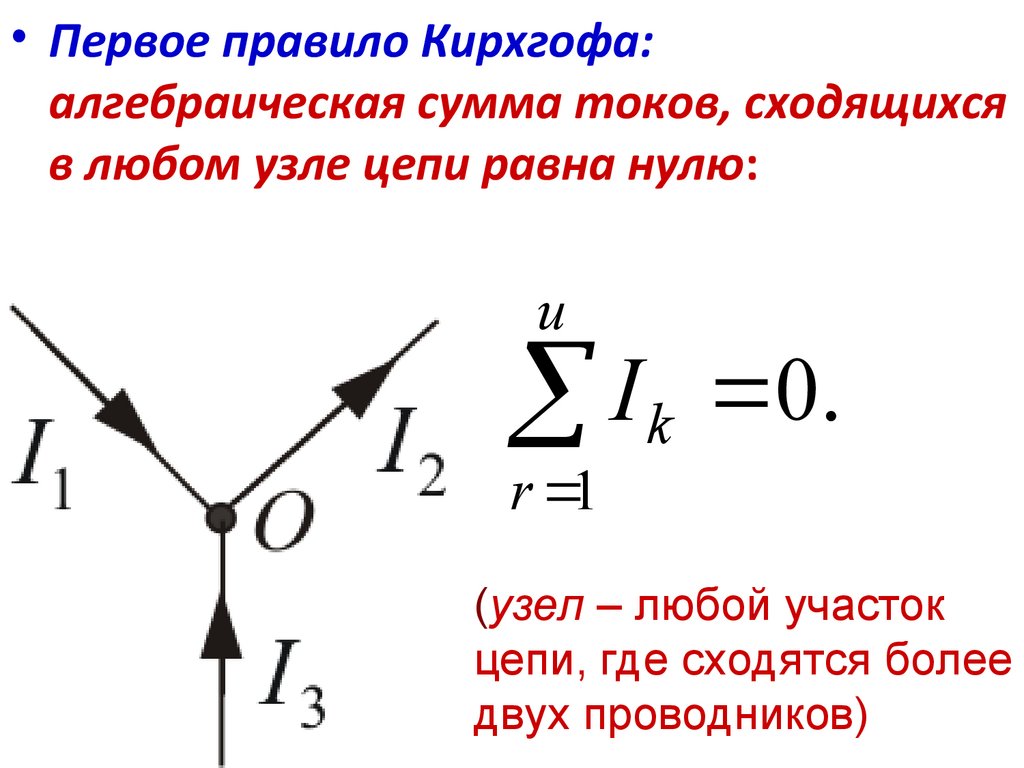
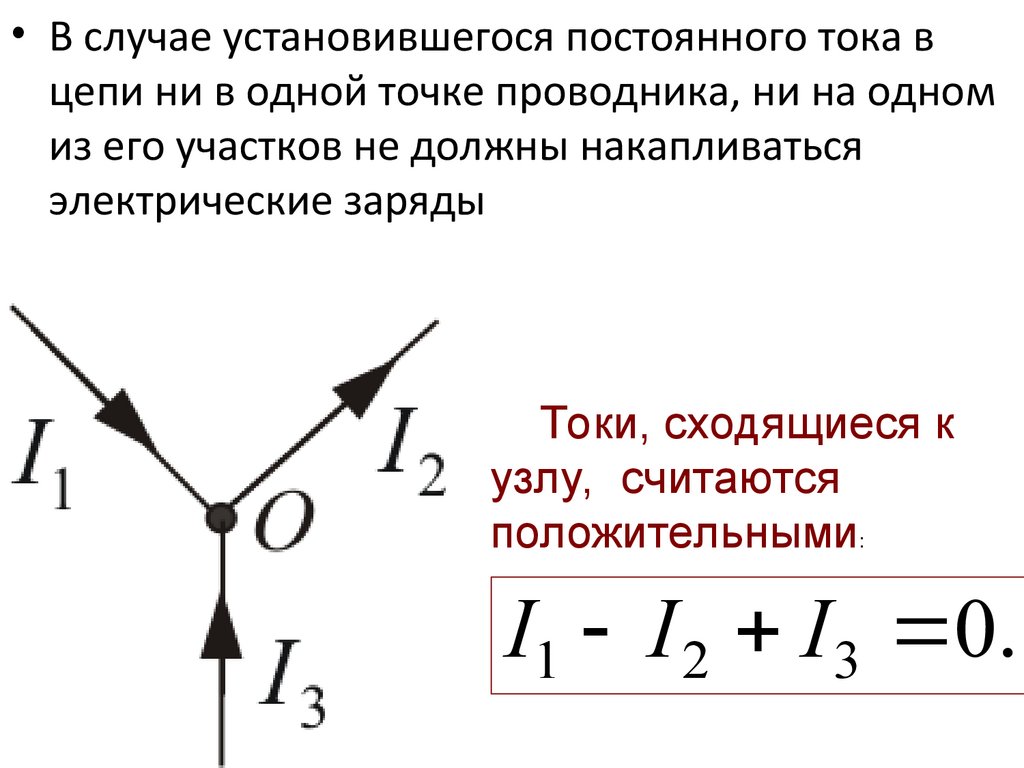
• Первое правило Кирхгофа:алгебраическая сумма токов, сходящихся
в любом узле цепи равна нулю:
u
I
0
.
k
r 1
(узел – любой участок
цепи, где сходятся более
двух проводников)
65.
• В случае установившегося постоянного тока вцепи ни в одной точке проводника, ни на одном
из его участков не должны накапливаться
электрические заряды
Токи, сходящиеся к
узлу, считаются
положительными:
I1 I 2 I 3 0.
66.
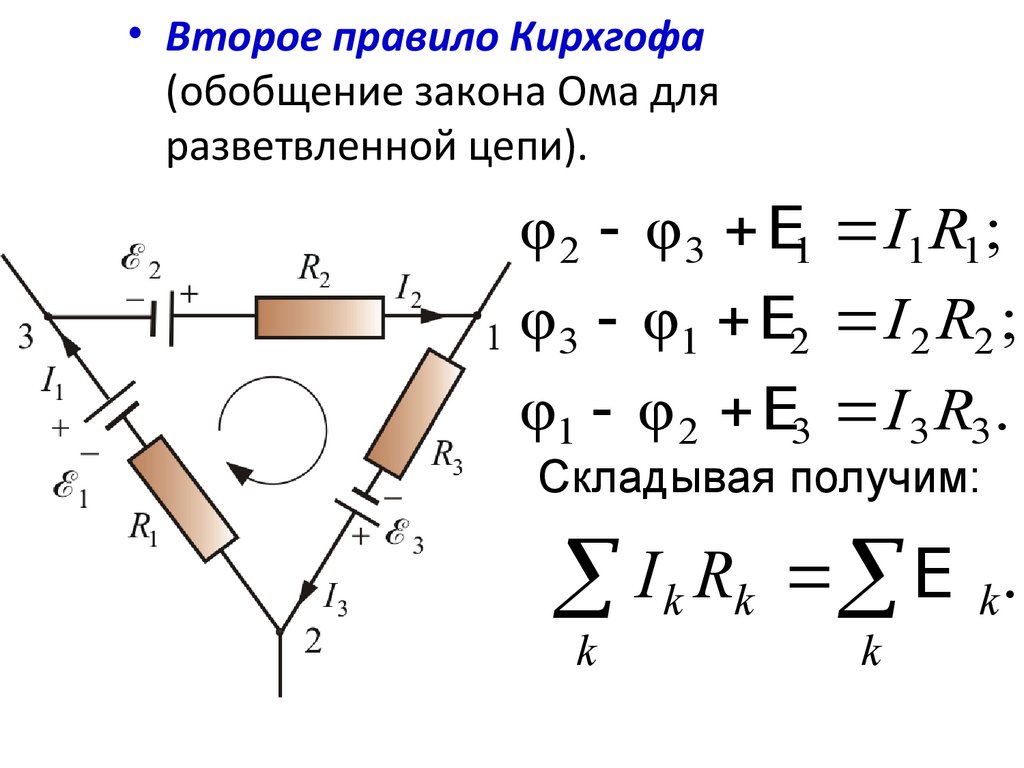
• Второе правило Кирхгофа(обобщение закона Ома для
разветвленной цепи).
φ 2 φ 3 E1 I1 R1 ;
φ 3 φ1 E2 I 2 R2 ;
φ1 φ 2 E3 I 3 R3 .
Складывая получим:
I k Rk E k .
k
k
67.
• В любом замкнутом контуре электрическойцепи алгебраическая сумма произведения
тока на сопротивление равна алгебраической
сумме ЭДС, действующих в этом же контуре.
I k Rk E k .
k
k
• Обход контуров осуществляется по часовой
стрелке, если направление обхода совпадает с
направлением тока, то ток берется со знаком
«плюс».
68.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутомконтуре, равна алгебраической сумме падений напряжения на всех
резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС
так и величина падения напряжения на элементах может быть как со
знаком «+» так и со знаком «-». При этом определить знак можно по
следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой,
либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по
правилам:
- ЭДС, создающие ток в контуре, направление которого совпадает с
направление обхода контура записываются со знаком «+», в противном
случае ЭДС записываются со знаком «-».
- напряжения, падающие на элементах цепи записываются со знаком «+»,
если ток, протекающий через эти элементы совпадает по направлению с
обходом контура, в противном случае напряжения записываются со
знаком «-».
































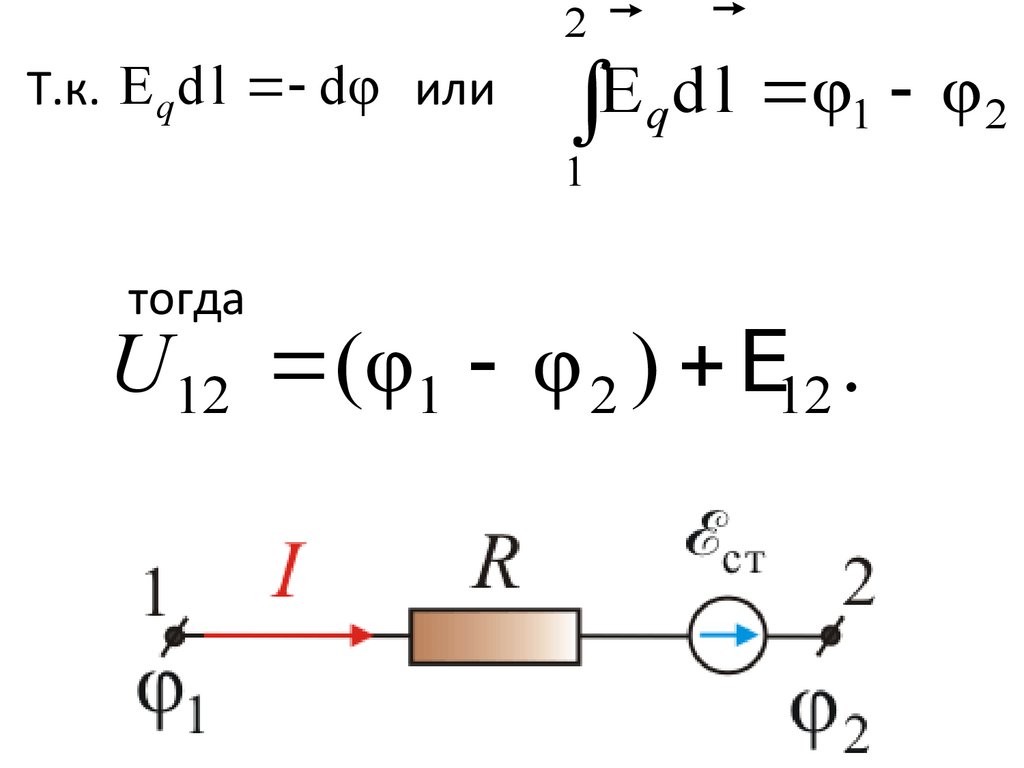






















 Физика
Физика








