Способы решения задач на смеси и сплавы. Арифметический. Применение уравнения. Применение систем уравнений

1.

ЕГЭ
ЗАДАЧИ
НА СМЕСИ И СПЛАВЫ
золото
серебро
В 13

2.

Способы решения задач
на смеси и сплавы
Арифметический
Применение уравнения
Применение систем уравнений

3.

В сосуд, содержащий 5 литров 12 процентного
водного раствора некоторого вещества, добавили
7 литров воды. Сколько процентов составляет
концентрация получившегося раствора?
способ
I способIII
II способ
5 7 12( л.)
Объем раствора увеличился
раза
p1V1 p2вV2,4
2
(было 5 л., стало
12 л. 12:5
=
2,4),
p
0,6л.
12 % 0,6л +
5
0
,
12
0
,
6
(
л
.)
=
V
V
содержание вещества
не
изменилось,
поэтому
0%
1
2
процентная концентрация
12 5 0 7 получившегося
60 0,6
100
5
%
p 7 л.
5
(%)
5 л.
раствора
уменьшилась
в122,4
раза.
л.
12
5
7
12
12:2,4=5(%)
Ответ: 5%
Ответ:
Ответ:5%
5%
Решение

4.

Сколько литров воды нужно добавить в 2 л водного
раствора, содержащего 60% кислоты, чтобы
получить 20 процентный раствор кислоты?
Объем чистой кислоты в растворе не меняется,
процентное содержание кислоты в растворе
уменьшится в 3 раза (60:20=3)
Объем раствора увеличится в 3раза:2·3=6(л)
6 – 2 = 4 (л) воды нужно добавить
Ответ: 4 л.
Решение

5.

Смешали 4 литра 15 процентного водного раствора
с 6 литрами 25 процентного водного раствора
этого же вещества. Сколько процентов составляет
концентрация получившегося раствора?
p1V1 p2V2 4 6 10( л.)
0,15 4 0,6( л.)
p
V1 V2
0,25 6 1,5( л.)
2,1л.
25%
1,5л.
15 4= 25 6 210 0,6 1,5 2,1( л.)
15% 0,6л. +
p
221
,1 (%)
4 6
10
100 21%
4л.
Решение
6л.
10л. 4 л.
Ответ:
10
Ответ : 21%

6.

Влажность сухой цементной смеси на складе
составляет 18%. Во время перевозки из-за дождей
влажность смеси повысилась на 2%. Найдите
массу привезенной смеси, если со склада было
отправлено 400 кг.
Было
Стало
Вода
18% 72кг.
Вода
20%
328кг.
Цемент
80%
328кг.
Цемент
400кг.
?
Решение
400 0,18 72(кг.) воды
400 72 328(кг.) цем.
100 20 80(%) 328кг.
328 : 0,8 410(кг.) масса
проивезенной смеси
Ответ : 410кг.

7.

Сколько надо взять 5 процентного и
25 процентного раствора кислоты, чтобы
получить 4 л 10 процентного раствора кислоты?
5%
0,05х
10%
0,4л
25%
+ 0,25(4-х)л= (1-0,2х)л
хл
(4-х) л
4л
Получим уравнение 1 - 2х = 0,4
хвтором
=
3 растворе
0,05+0,25(4-х)=(10,10,25
· 40,05
=· 0,4
(4х -(лх)
л–0,2х)
)–
лкислоты
–кислоты
кислоты
л – кислоты
в полученном
в во
первом
в полученном
растворе
растворе
3л – надо взять 5процентного раствора
4 – 3 = 1(л) – 25 процентного
Ответ: 1л; 3л.
Решение

8.

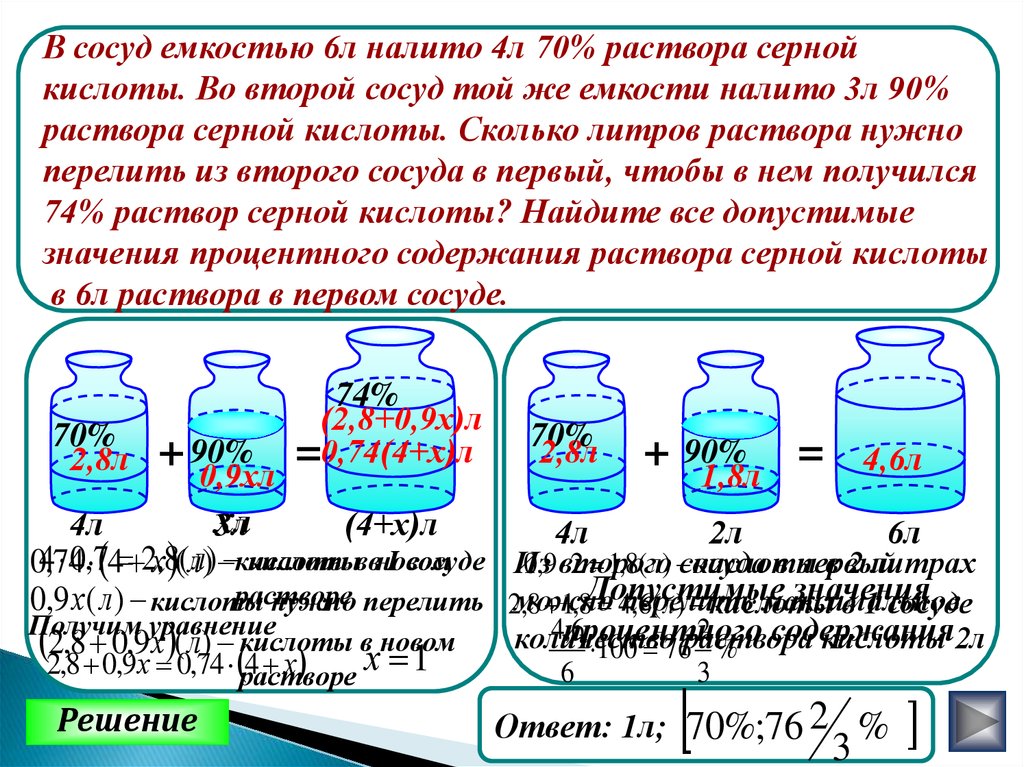
В сосуд емкостью 6л налито 4л 70% раствора серной
кислоты. Во второй сосуд той же емкости налито 3л 90%
раствора серной кислоты. Сколько литров раствора нужно
перелить из второго сосуда в первый, чтобы в нем получился
74% раствор серной кислоты? Найдите все допустимые
значения процентного содержания раствора серной кислоты
в 6л раствора в первом сосуде.
70%
2,8л
+ 90%
0,9хл
74%
(2,8+0,9х)л
=0,74(4+х)л
70%
2,8л
+
90%
1,8л
=
4,6л
х3лл
4л
(4+х)л
4л
2л
6л
0, 7 4 2х,8 ((лл)) кислоты
кислотыввновом
I сосуде Из
04,74
кислоты
в первый
в 2 литрах
0,9 второго
2 1,8( л) сосуда
значения
растворе
0,9 х( л) кислоты
максимальное
нужно перелить 2можно
в 1 сосуде
,8 1,8Допустимые
4перелить
,6( л) кислоты
Получим уравнение
4процентного
,6
2
содержания
количество
раствора
кислоты 2л
22,,88 00,9,9хх (0л,74
) кислоты вхновом
100
76
%
1
4 х
растворе
Решение
6
3
Ответ: 1л; 70%;76 2 %
3

9.

Первый сплав содержит 10% меди, второй – 40% меди.
Масса второго сплава больше массы первого на 3кг.
Из этих двух сплавов получили третий сплав, содержащий
30% меди. Найдите массу третьего сплава.
Ответ дайте в килограммах.
0,1х кг
х кг.
0,4(х+3)кг
(х+3) кг.
0,3(2х+3)кг
(х+(х+3)) кг.
Получим Масса
уравнение
меди в первом сплаве
0,5 х 0,1х(кг)
0,6 х 0,9 1,2
0,1х 0,4 Во
х втором
3 0,3– 20,4(х+3)(кг)
х 3
0,1х 0,4Вх третьем
1,2 0,–6 х0,3(2х+3)(кг)
0,9
Решение
Ответ: 9 кг.
х 3
2 3 3 9(кг )

10.

Имеется два сплава золота и серебра: в одном массы этих
металлов находятся в отношении 2:3, а в другом – в
отношении 3:7. Сколько килограммов нужно взять от
каждого сплава, чтобы получить 8 кг нового сплава, в
котором золото и серебро находились бы в отношении 5:11?
серебро
серебро
золото
золото
серебро
серебро
золото
золото
золото
серебро
х кг
(8 – х)кг
8кг
2
3
8 х 2,5
х
Получим уравнение
5
10 3 2 5
Масса
Масса
в первом
новом куске
сплаве
куске 1
8
8х-от
кг
кгх2. , 15кг
0,1хзолота
2золота
,4 2во
,5 втором
кг
сплава
16
10
5
8 1 7( кг )-от
х 1
2 сплава
Решение
Ответ:1 кг. и 7 кг.

11.

Имеется два сплава. Первый содержит 10% никеля, второй30% никеля. Из этих двух сплавов получили третий сплав
массой 200 кг, содержащий 25% никеля. На сколько
килограммов масса первого сплава меньше массы второго?
х кг
у кг
200 кг
х 200 у; х 200 у;
х у 200;
0,1х 0,3 у 50. х 3 у 500. 200 у 3 у 500.
в первом
сплавепервого
0,1х кг сплава.
50 кг - масса
х 50никеля
;
Масса
Масса никеля во150
втором
сплаве
0,3у кг.сплава.
кг - масса
второго
у 150
.
Масса
никеля в новом
150 – 50
сплаве
= 100200·0,25=50
(кг)
(кг).
Решение
Ответ: на 100 кг.

12.

При смешивании 30 процентного раствора серной кислоты с
10 процентным раствором серной кислоты получилось 400 г
15 процентного раствора. Сколько граммов 30 процентного
раствора было взято?
30%0,3х г
хг
+
10%0,1у г
уг
=
15% 60 г
х у 400;
0,3х 0,1у 60.
400г.
400
( гх); кислоты в новом
100;
у 0
храстворе
400
,
15
60
400 х в первом
60. растворе
0,03,х3 х ( г0),1 кислоты
у 300.
0,100
1у ( гг) – 30%
кислоты
раствора
во втором
было взято.
растворе
Решение
Ответ: 100 г.

13.

Имеются два слитка сплава серебра и олова. Первый слиток
содержит 360г серебра и 40г олова, а второй слиток – 450г
серебра и 150г олова. От каждого слитка взяли по куску,
сплавили их и получили 200г сплава, в котором оказалось
81% серебра. Определите массу (в граммах) куска, взятого
от второго слитка.
400г
олово
олово
серебро
олово
олово
серебро
серебро
серебро
олово
600г
серебро
хг
уг
200 г
х 450
у360
200; 0,9 0,9 х 0,9 у 180; х 80;
0,75у(г)серебра
серебра
ввпервом
втором
слитке
слитке
куске
100
100
75
90
%
%
200
0
,
81
162
(
г
)
0,9х(г)
серебра
- серебра
вво
новом
первом
сплаве
куске
0,9 х600
0,75 у 162.
400
0,9 х 0,75 у 162.
у 120.
Решение
Ответ:120 г.

14.

Первый раствор содержит 40% кислоты, а второй - 60%
кислоты. Смешав эти растворы и добавив 5 л воды,
получили 20 процентный раствор. Если бы вместо воды
добавили 5 л 80 процентного раствора, то получился бы
70 процентный раствор. Сколько литров 60 процентного
раствора кислоты было первоначально?
80%
60% + 0%
4л
0,6у л
70%
20%
0,7(х+у+5)
0,2(х+у+5) л
л
40% +
=
0,4х 0,6 у 0,2 х у 5 ;
0,4х л
хл
ул
(х+у+5) л 0,4х 0,6 у 4 0,7 х у 5 .
5л
х 0,6 у 0,2 х 0,2 у 1;
0,40,2(х+у+5)
х 1;
0
,
2
х
0
,
4
у
1
;
0,6у
0,7(х+у+5)
(л)
кислоты
(л)
(л)
кислоты
кислоты
во
втором
в
в
новом
новом
растворе
растворе
растворе
кислоты
растворе
0,4х (л) 0-,8
кислоты
в 5 литрах
5 4( л)в первом
0,4 х 0,6 у 4 0,7 х 0,7 у 3,5. 0,3х 0,1у 0,5. у 2.
Решение
Ответ: 2 л

15.

Литература и интернет-ресурсы
1. Денищева Л.О., Глазков Ю.А. и др. Единый
Государственный экзамен 2008. Математика.
Учебно-тренировочные материалы для подготовки
учащихся / ФИПИ – М.: Интеллект-Центр, 2007.
2. Шевкин А.В. Текстовые задачи в школьном курсе
Математики. М.: Педагогический университет
«Первое сентября», 2006.
3. Открытый банк заданий ЕГЭ 2012
http://www.nado5.ru/materials/novoe-v-yege-po-matematike