Сущность формализации

1.

Сущность формализации
1
Определение
Формализация – это процесс
2
Исключение
неоднозначности
3
Автоматизация и
точность
абстрагирования от конкретного
Правильная формализация
Формализация обеспечивает
содержания задачи и построения
позволяет исключить
возможность автоматизации
её математической или
неоднозначность интерпретации
решения схожих задач и
логической модели. При этом
условий задачи и применить
получение точных, проверяемых
сохраняются только те свойства и
строгие методы решения
результатов.
отношения объектов, которые
(алгоритмы, формулы,
существенны для решения
теоремы).
поставленной задачи.

2.

Этапы формализации
Анализ задачи и выделение ключевых объектов
На этом этапе определяются основные сущности, их свойства и отношения между ними. Важно отделить существенные аспекты от
несущественных.
Выбор математического аппарата
В зависимости от природы задачи выбирается адекватный математический аппарат: алгебра, геометрия, математический анализ, теория графов,
теория вероятностей и т.д.
Построение математической модели
Формулировка задачи на языке выбранного математического аппарата с введением переменных, констант, функций, отношений и ограничений.
Решение формализованной задачи
Применение математических методов для получения решения в рамках построенной модели.
Интерпретация результата и валидация модели
Перевод полученного математического решения обратно на язык исходной задачи и проверка адекватности полученного решения.

3.

Пример 1: Оптимизация транспортных
перевозок
Исходная задача
Формализация
Компания имеет три склада и четыре магазина.
Определение переменных: x₍ᵢⱼ₎ – количество товара,
Необходимо минимизировать затраты на перевозку товаров
перевозимого со склада i в магазин j; c₍ᵢⱼ₎ – стоимость
со складов в магазины, учитывая стоимость перевозки
перевозки; a₍ᵢ₎ – запас товара на складе i; b₍ⱼ₎ –
единицы товара между каждым складом и магазином, а
потребность магазина j.
также ограничения по запасам на складах и потребностям
магазинов.
Целевая функция: Z = ∑₍ᵢ=₁₎³ ∑₍ⱼ=₁₎⁴ c₍ᵢⱼ₎ × x₍ᵢⱼ₎ → min

4.

Пример 1: Оптимизация транспортных
перевозок (продолжение)
Ограничения модели
Метод решения
По запасам: ∑₍ⱼ=₁₎⁴ x₍ᵢⱼ₎ ≤
Данная задача относится к классу
a₍ᵢ₎ для всех i = 1,2,3
задач линейного программирования
По потребностям: ∑₍ᵢ=₁₎³ x₍ᵢⱼ₎
и может быть решена симплекс-
= b₍ⱼ₎ для всех j = 1,2,3,4
методом или методом потенциалов.
Неотрицательность: x₍ᵢⱼ₎ ≥ 0
Преимущества
формализации
Задача сводится к стандартной
математической модели
Существуют эффективные
алгоритмы решения
для всех i, j
Решение гарантированно будет
оптимальным
Модель легко масштабируется

5.

Пример 2: Классификация клиентов банка
Исходная задача
Определение
переменных
Построение модели
процесс принятия решений о
X = (x₁, x₂, ..., xₙ) –
Задача формализуется как
случайный лес, градиентный
выдаче кредитов,
вектор характеристик клиента;
задача бинарной
бустинг или другие методы
классифицируя клиентов на
Y ∈ {0, 1} – целевая
классификации. Необходимо
машинного обучения для
"надежных" и "ненадежных"
переменная; D = {(X₁, Y₁),
найти функцию f: X → {0,
задач классификации.
на основе их характеристик.
(X₂, Y₂), ..., (Xₙ, Yₙ)} –
1}, которая для новых
обучающая выборка.
клиентов будет предсказывать
Банк хочет автоматизировать
Методы решения
Логистическая регрессия,
их надежность.

6.

Пример 2: Классификация клиентов банка
(продолжение)
Автоматическое принятие решений
Формализация позволяет автоматизировать процесс оценки кредитоспособности клиентов, что значительно ускоряет работу банка.
Объективность оценки
Математическая модель обеспечивает объективность оценки кредитоспособности, исключая субъективные факторы.
Масштабируемость
Модель может обрабатывать большое количество заявок одновременно, что невозможно при ручной обработке.
Возможность улучшения
Модель можно постоянно улучшать на основе новых данных, повышая точность классификации.

7.

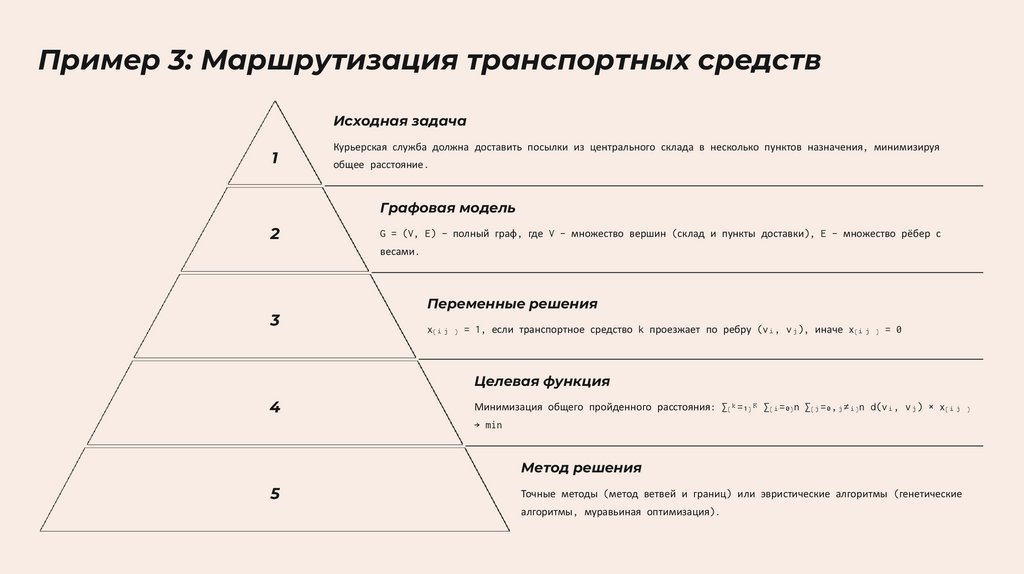
Пример 3: Маршрутизация транспортных средств
Исходная задача
1
Курьерская служба должна доставить посылки из центрального склада в несколько пунктов назначения, минимизируя
общее расстояние.
Графовая модель
2
G = (V, E) – полный граф, где V – множество вершин (склад и пункты доставки), E – множество рёбер с
весами.
3
Переменные решения
x₍ᵢⱼ ₎ = 1, если транспортное средство k проезжает по ребру (vᵢ, vⱼ), иначе x₍ᵢⱼ ₎ = 0
Целевая функция
4
Минимизация общего пройденного расстояния: ∑₍ᵏ=₁₎ᴷ ∑₍ᵢ=₀₎ⁿ ∑₍ⱼ=₀,ⱼ≠ᵢ₎ⁿ d(vᵢ, vⱼ) × x₍ᵢⱼ ₎
→ min
Метод решения
5
Точные методы (метод ветвей и границ) или эвристические алгоритмы (генетические
алгоритмы, муравьиная оптимизация).

8.

Пример 3: Маршрутизация
транспортных средств (продолжение)
1
Ограничения модели
Каждый пункт должен быть
2
Преимущества
оптимизации
3
Практическое
применение
посещен ровно один раз.
Возможность найти оптимальные
Данная формализация
Каждое транспортное средство
или близкие к оптимальным
применяется в логистических
должно начинать и заканчивать
маршруты. Учёт всех
компаниях, службах доставки,
маршрут на складе. Вместимость
ограничений задачи.
при планировании маршрутов
транспортного средства не
Возможность быстрой
общественного транспорта и в
должна быть превышена.
перепланировки при изменении
других областях, где требуется
Должны отсутствовать подциклы,
условий. Снижение
оптимизация перемещений.
не включающие склад.
операционных расходов за счёт
оптимизации.

9.

Пример 4: Составление расписания
1
Исходная задача
Университет должен составить расписание занятий с учетом доступности преподавателей, аудиторий и требований к проведению занятий
различных типов.
2
Определение множеств
P = {p₁, p₂, ..., pₙ} – множество преподавателей; R = {r₁, r₂, ..., rₙ} – множество аудиторий; C = {c₁, c₂, ..., cₙ} –
множество курсов; T = {t₁, t₂, ..., tₙ} – множество временных слотов; G = {g₁, g₂, ..., gₙ} – множество групп студентов.
3
Переменные решения
x₍ᵖ,ᶜ,ᵍ,ʳ,ᵗ₎ = 1, если преподаватель p ведет курс c для группы g в аудитории r во временной слот t, иначе 0.
4
Ограничения
Конфликты расписания преподавателей, групп и аудиторий. Соответствие аудиторий типам занятий. Доступность преподавателей в
определенные временные слоты. Требование определенного количества часов для каждого курса.

10.

Пример 4: Составление расписания
(продолжение)
Целевая функция
Метод решения
Минимизация различных штрафов,
Данная задача может быть решена
например, за "окна" в расписании
методами целочисленного
преподавателей и студентов, за
линейного программирования или с
неравномерное распределение
помощью эвристических алгоритмов
нагрузки и т.д.
(генетические алгоритмы, метод
Преимущества
формализации
Возможность учета всех
ограничений и предпочтений
имитации отжига и др.).
Автоматизация процесса
составления расписания
Быстрая адаптация при
изменении условий
Оптимизация использования
ресурсов университета

11.

Пример 5: Прогнозирование временных
рядов
Исходная задача
Построение модели ARIMA
Компания хочет прогнозировать объем продаж на
ARIMA(p,d,q): (1 - Σᵖᵢ₌₁ φᵢL^i)(1 - L)^d yₙ = (1 +
следующий месяц на основе исторических данных для
Σᵍᵢ₌₁ θᵢL^i)ε
оптимизации закупок и управления запасами.
Определение временного ряда
{y₁, y₂, ..., yₙ} – наблюдаемые значения объема продаж
за последние t периодов.
где p – порядок авторегрессионной части, d – порядок
разности, q – порядок скользящего среднего, L – оператор
лага, φᵢ и θᵢ – параметры модели, ε – белый шум.

12.

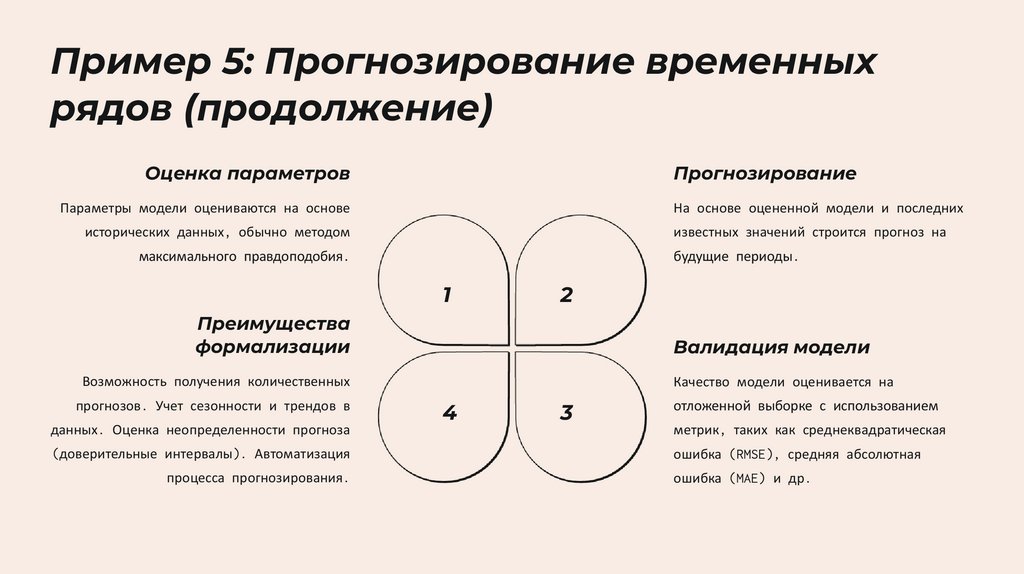
Пример 5: Прогнозирование временных
рядов (продолжение)
Оценка параметров
Прогнозирование
Параметры модели оцениваются на основе
На основе оцененной модели и последних
исторических данных, обычно методом
известных значений строится прогноз на
максимального правдоподобия.
будущие периоды.
1
2
Преимущества
формализации
Валидация модели
Возможность получения количественных
прогнозов. Учет сезонности и трендов в
данных. Оценка неопределенности прогноза
(доверительные интервалы). Автоматизация
процесса прогнозирования.
Качество модели оценивается на
4
3
отложенной выборке с использованием
метрик, таких как среднеквадратическая
ошибка (RMSE), средняя абсолютная
ошибка (MAE) и др.

13.

Пример 6: Кластеризация клиентов
Исходная задача
1
Компания хочет сегментировать своих клиентов для разработки таргетированных маркетинговых кампаний.
Определение пространства признаков
2
X = {x₁, x₂, ..., xₙ} – множество клиентов, каждый представлен вектором признаков.
Постановка задачи кластеризации
3
Разбить множество X на k непересекающихся подмножеств (кластеров).
Алгоритм k-средних
4
Итеративный алгоритм, минимизирующий сумму квадратов расстояний
от объектов до центров их кластеров.
Формализация задачи кластеризации позволяет объективно сегментировать клиентов на основе их характеристик, выявлять скрытые закономерности в
данных и автоматизировать процесс сегментации.

14.

Общие принципы формализации: Ясное
понимание задачи
Определение целей и критериев успеха
Перед началом формализации необходимо четко определить, какие цели должны быть достигнуты и по каким критериям будет
оцениваться успешность решения.
Выявление всех существенных ограничений
Важно выявить все ограничения, которые должны быть учтены при решении задачи, включая технические, экономические,
временные и другие ограничения.
Понимание доступных ресурсов и данных
Необходимо иметь ясное представление о том, какие данные и ресурсы доступны для решения задачи, и учитывать их
ограничения при формализации.
Выявление заинтересованных сторон и их ожиданий
Следует учитывать интересы и ожидания всех заинтересованных сторон, которые могут влиять на постановку задачи и
оценку результатов.

15.

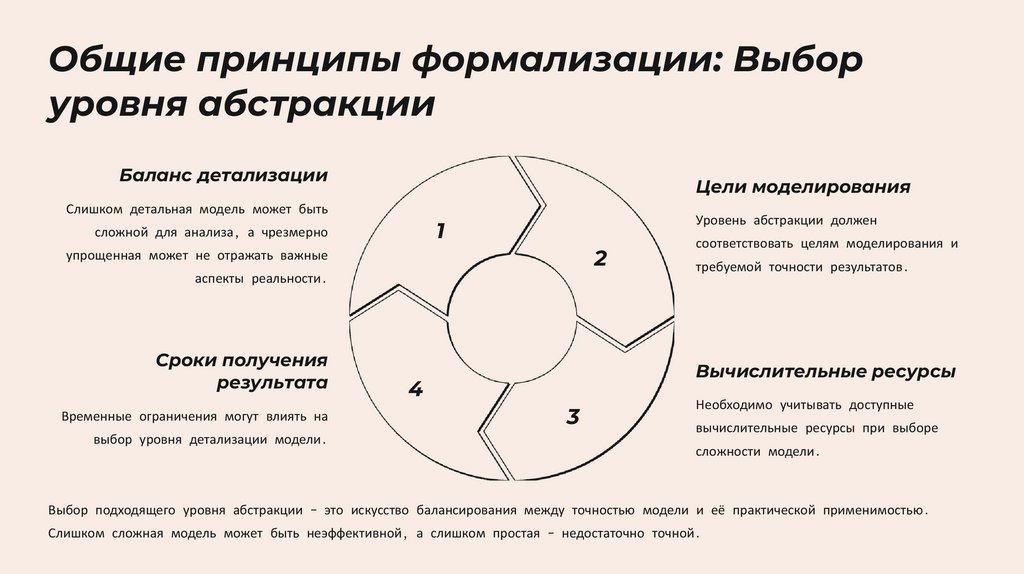
Общие принципы формализации: Выбор
уровня абстракции
Баланс детализации
Цели моделирования
Слишком детальная модель может быть
Уровень абстракции должен
1
сложной для анализа, а чрезмерно
2
упрощенная может не отражать важные
аспекты реальности.
Сроки получения
результата
Временные ограничения могут влиять на
выбор уровня детализации модели.
соответствовать целям моделирования и
требуемой точности результатов.
Вычислительные ресурсы
4
3
Необходимо учитывать доступные
вычислительные ресурсы при выборе
сложности модели.
Выбор подходящего уровня абстракции – это искусство балансирования между точностью модели и её практической применимостью.
Слишком сложная модель может быть неэффективной, а слишком простая – недостаточно точной.

16.

Общие принципы формализации:
Стандартные математические
структуры
Линейное
программирование
Сетевые модели
(графы)
Классификация и
регрессия
Оптимизация линейной целевой
Представление объектов и связей
Построение моделей зависимости
функции при линейных
между ними в виде вершин и
между переменными. Применяются
ограничениях. Применяется в
рёбер графа. Используются в
в задачах прогнозирования, оценки
задачах распределения ресурсов,
задачах маршрутизации, анализа
рисков, анализа данных.
планирования производства,
социальных сетей, планирования
транспортных задачах.
проектов.

17.

Общие принципы формализации: Валидация
модели
Соответствие модели исходной задаче
Необходимо проверить, насколько точно формализованная модель отражает суть исходной задачи и учитывает все её важные аспекты.
Учет всех существенных ограничений
Следует убедиться, что в модели учтены все существенные ограничения, которые могут влиять на решение задачи.
Реалистичность сделанных допущений
Важно оценить, насколько реалистичны допущения, сделанные при построении модели, и как они могут повлиять на результаты.
Согласованность с эмпирическими данными
Необходимо проверить, согласуются ли решения модели с эмпирическими данными или экспертными оценками.

18.

Общие принципы формализации:
Итеративное улучшение
1
2
3
4
Начало с
простой модели
Проверка
адекватности
Постепенное
уточнение
Рекомендуется начинать с
Необходимо проверить,
На основе результатов
Баланс
сложности и
качества
простой модели, которая
насколько адекватно
проверки модель
На каждом этапе
отражает только
простая модель отражает
постепенно уточняется,
уточнения необходимо
ключевые аспекты
реальную задачу и даёт
добавляются новые
поддерживать баланс
задачи, но может быть
полезные результаты.
аспекты и ограничения,
между сложностью
легко проанализирована
которые оказались
модели и качеством
и проверена.
существенными.
получаемого решения.

19.

Типичные проблемы при формализации: Неполнота
исходных данных
Проблема
Часто при формализации оказывается, что доступных данных недостаточно для
полного описания задачи. Это может приводить к неточностям в модели и снижать
качество получаемых решений.
Решения
Использование экспертных оценок для заполнения пробелов
Применение методов обработки неполных данных
Анализ чувствительности модели к неопределенностям в данных
Построение нескольких сценариев в зависимости от предположений о
недостающих данных

20.

Типичные проблемы при формализации:
Сложность математической модели
Проблема
Решения
Пример
Формализованная модель может
Вместо точного решения задачи
Декомпозиция задачи на подзадачи
оказаться слишком сложной для
эффективного решения, что делает её
маршрутизации транспортных средств,
непрактичной для реального
применения.
Применение аппроксимационных
которая является NP-трудной, можно
методов
использовать эвристические
Использование эвристических
алгоритмов
Упрощение модели с сохранением
ключевых свойств
алгоритмы, дающие близкие к
оптимальным решения за приемлемое
время.

21.

Типичные проблемы при формализации:
Противоречивые требования
Проблема
Различные заинтересованные стороны могут иметь противоречивые цели и
требования, что затрудняет формулировку единой целевой функции и ограничений.
Решения
Использование методов многокритериальной оптимизации
Поиск компромиссных решений (Парето-оптимальность)
Анализ чувствительности решения к изменению весов критериев
Применение теории игр для моделирования взаимодействия заинтересованных
сторон

22.

Типичные проблемы при формализации:
Динамический характер реальных систем
Проблема
Использование
динамических моделей
Периодическое обновление
параметров
временем, что затрудняет их
Вместо статических моделей можно
Регулярное обновление параметров модели
формализацию в виде статических
использовать динамические, которые
на основе новых данных позволяет
моделей. Параметры системы могут
учитывают изменение системы во времени,
поддерживать её актуальность даже при
меняться, появляются новые ограничения и
например, дифференциальные уравнения
изменении системы.
возможности.
или системы с дискретным временем.
Многие реальные системы изменяются со
Применение адаптивных алгоритмов
Адаптивные алгоритмы способны автоматически подстраиваться под изменения в системе, что делает их более устойчивыми к динамическим
изменениям.

23.

Вопрос 1: Выбор математического аппарата
Как выбрать подходящий математический
аппарат для формализации конкретной
задачи?
При выборе математического аппарата следует учитывать природу задачи,
доступные данные, требуемую точность решения и вычислительные
ресурсы. Для задач оптимизации с линейными ограничениями подходит
линейное программирование, для задач с сетевой структурой – теория
графов, для моделирования неопределенности – теория вероятностей или
нечеткая логика.
Часто полезно начать с простой модели и постепенно её усложнять,
добавляя новые аспекты и ограничения по мере необходимости.

24.

Вопрос 2: Оценка
адекватности модели
Адекватность модели можно оценить путем сравнения её предсказаний с
эмпирическими данными или результатами экспертных оценок. Для
статистических моделей используются метрики качества (точность,
полнота, F1-мера и др.), для оптимизационных моделей – соответствие
решения реальным ограничениям и достижение поставленных целей.
Также полезно проводить анализ чувствительности модели к изменению
входных параметров, чтобы понять, насколько устойчивы получаемые
решения.

25.

Вопрос 3: Компромиссы при формализации
Точность vs Сложность
1
2
Баланс между точностью модели и её сложностью.
Полнота vs Эффективность
Баланс между полнотой учета всех факторов и вычислительной эффективностью.
Универсальность vs Специализация
3
Баланс между универсальностью модели и её специализацией под конкретную задачу.
Противоречивые критерии
4
Баланс между различными, иногда противоречивыми, критериями
оптимальности.
Основные компромиссы при формализации связаны с необходимостью балансировать между различными, часто противоречивыми требованиями. Выбор
конкретного компромисса зависит от специфики задачи и доступных ресурсов.

26.

Вопрос 4: Учет неопределенности и
стохастичности
1
Вероятностные модели
Для учета неопределенности могут
4
2
Теория нечетких
множеств
3
Робастная оптимизация
использоваться вероятностные
В нечетких моделях используются
В робастной оптимизации ищутся
модели, в которых случайные
функции принадлежности, которые
решения, устойчивые к
величины описываются их
позволяют моделировать
неопределенности в параметрах.
распределениями. Это позволяет
неопределенность, не связанную со
Это особенно важно, когда
моделировать различные сценарии и
случайностью, а с нечеткостью
последствия неправильного решения
оценивать их вероятности.
понятий и критериев.
могут быть критическими.
Сценарный анализ
Сценарный анализ предполагает разработку нескольких сценариев развития ситуации и поиск решений, которые будут
эффективны в большинстве сценариев.

27.

Вопрос 5: Роль вычислительных
ограничений
Влияние на выбор
модели
Компромиссы
Вычислительные ограничения могут
ограничений приходится искать
Развитие вычислительной техники и
существенно влиять на выбор
компромиссы: использовать
алгоритмов постоянно расширяет
модели и методов решения.
приближенные методы, упрощать
класс задач, которые могут быть
Некоторые математически
модель, декомпозировать задачу на
эффективно решены. Однако для
элегантные формализации могут
подзадачи или применять
многих практических задач
оказаться неприменимыми на
эвристические алгоритмы.
вычислительные ограничения
практике из-за их вычислительной
сложности.
В условиях вычислительных
Современные
тенденции
остаются актуальными.

28.

Практические рекомендации по
формализации
1
Тщательный анализ задачи
2
Изучение существующих подходов
Перед началом формализации проведите тщательный
анализ задачи, выявите все существенные аспекты,
Изучите литературу и существующие подходы к
ограничения и цели. Обсудите задачу с экспертами в
решению аналогичных задач. Часто можно
предметной области.
адаптировать уже известные модели к вашей
конкретной ситуации.
3
Начинайте с простого
4
Регулярная проверка
Начинайте с простой модели, которая отражает только
Регулярно проверяйте адекватность модели, сравнивая
ключевые аспекты задачи. Постепенно усложняйте её,
её предсказания с реальными данными или
добавляя новые детали и ограничения.
экспертными оценками. Корректируйте модель при
необходимости.

29.

Практические рекомендации по
формализации (продолжение)
Документируйте
процесс
Общайтесь с
заинтересованным
и сторонами
Будьте гибкими
процесс формализации,
Поддерживайте постоянную
первоначальная модель
Используйте современные
включая все сделанные
коммуникацию с
оказывается неадекватной или
программные инструменты для
допущения, ограничения и
заинтересованными
слишком сложной.
построения и анализа
обоснования выбора
сторонами, объясняйте им
моделей, которые могут
конкретной модели.
суть модели и получайте
значительно упростить процесс
обратную связь.
формализации.
Тщательно документируйте
Будьте готовы изменить
подход к формализации, если
Используйте
современные
инструменты

30.

Применение формализации в различных
областях
Бизнес и экономика
Инженерия и производство
Оптимизация бизнес-процессов, управление
Проектирование технических систем,
запасами, финансовое моделирование,
оптимизация производственных процессов,
Диагностика заболеваний, планирование
прогнозирование спроса, ценообразование,
контроль качества, планирование
лечения, оптимизация работы медицинских
анализ рисков, планирование инвестиций.
технического обслуживания, управление
учреждений, эпидемиологическое
цепочками поставок.
моделирование, разработка лекарств.
Медицина и
здравоохранение

31.

Применение формализации в различных
областях (продолжение)
Формализация находит применение в таких областях, как городское планирование (оптимизация транспортных потоков,
размещение объектов инфраструктуры), экология (моделирование экосистем, оценка воздействия на окружающую среду),
социология (анализ социальных сетей, моделирование общественного мнения) и искусственный интеллект (машинное обучение,
компьютерное зрение, обработка естественного языка).

32.

Будущее формализации
Искусственный
интеллект
Большие данные
Методы искусственного интеллекта
Развитие методов работы с большими
позволяют автоматизировать процесс
данными открывает новые
1
возможности для формализации
формализации и находить
2
сложных систем на основе
данных.
эмпирических данных.
Междисциплинарный
подход
Интеграция методов из различных
областей науки обогащает
инструментарий формализации и
расширяет сферу её применения.
неочевидные закономерности в
4
Рост вычислительных
мощностей
3
Увеличение доступных вычислительных
ресурсов позволяет решать всё более
сложные формализованные задачи.