Разработка программных модулей

1.

Разработка
программных модулей

2.

Оценка сложности алгоритма
Для разогрева:
Оцените сложность данного алгоритма:
var count = 0;
for (int i = 0; i < 1000000; i += n)
count++;
2

3.

Оценка сложности алгоритма
Как считается временная сложность алгоритма?
Возьмем в качестве примера обычный цикл
for (int i=0; i < n; i++)
count++;
3

4.

Оценка сложности алгоритма
Посчитаем количество элементарных операций:
• 1 для int i = 0
• n+1 для i < n
• 2n для i++ (что эквивалентно i = i + 1, а это две операции: присваивание и
сложение)
• 2n для сount++
Получаем, что временную сложность алгоритма C(n) = 2 + 5n
4

5.

Оценка сложности алгоритма
Оценим уровень сложности для этого алгоритма:
int i = 0;
while (i < n)
{
for(int j=0; j<n; j++)
count++;
i++;
}
5

6.

Оценка сложности алгоритма
i = 0 выполнится лишь однажды
i<n внутри while выполнится n+1 раз
i+=1 выполнится n раз (+= это две элементарные операции)
цикл for начнет выполняться n раз и каждый раз:
j=0 выполнится один раз
j<n выполнится n+1 раз
j++ выполнится 2n раз (++ это две элементарные операции)
count++ выполнится 2n раз (++ это две элементарные операции)
6

7.

Оценка сложности алгоритма
Для реального кода вычислительная сложность может быть крайне сложной
функцией.
Кроме того, легко ошибиться в расчетах и забыть какое-нибудь из слагаемых.
С другой стороны, есть множество причин, почему нет смысла считать
точный вид функции сложности:
• Некоторые «элементарные» операции, такие как sin или квадратный
корень более дорогие, а функция сложности это не учитывает.
• Стоимость элементарных операций разная на разных процессорах.
• Стоимость элементарной операции зависит от контекста выполнения (от
кэширования, переключения контекстов, работы конвейера команд у
процессора, ...).
• Когда код написан на языке высокого уровня (C#, Python, JavaScript, ...)
есть скрытая стоимость: выделение памяти, сборка мусора, JIT7
компиляция и т.п.)

8.

Оценка сложности алгоритма
Если кратко и грубо, то получить асимптотическую оценку можно так:
отбросьте в функции сложности все слагаемые, кроме одного с самой
быстрой скоростью роста. А потом отбросьте все константы. То что
получится и будет асимптотической оценкой сложности.
Обычно время работы алгоритма нас интересует на больших данных, когда
алгоритм может существенно замедлиться. Асимптотическая оценка как раз
отвечает на вопрос, как сильно деградирует производительность с ростом
размера входа.
Не все задачи можно решить алгоритмически!!!
8

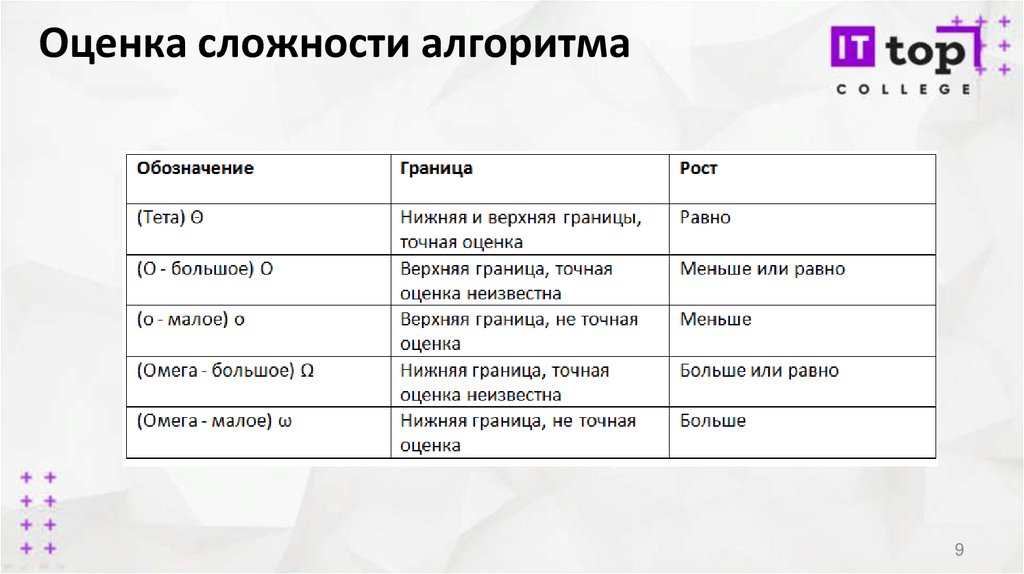
9.

Оценка сложности алгоритма
9

10.

Оценка сложности алгоритма
Если очень кратко — O(n²) означает, что самое быстро растущее слагаемое в
функции сложности — это n в степени не более 2.
Говоря математическим языком, f(n)=O(g(n)) тогда и только тогда, когда
∃C>0,∃n0 : ∀n>n0→t(n)<=Cg(n).
Существует такая константа C больше нуля и такое n0, что для всех n > n0
значение функции t(n) меньше или равно значению С g(n).
В таком случае говорят что, t принадлежит классу функций, которые растут не
быстрее, чем функция g (n) с точностью до постоянного множителя.
10

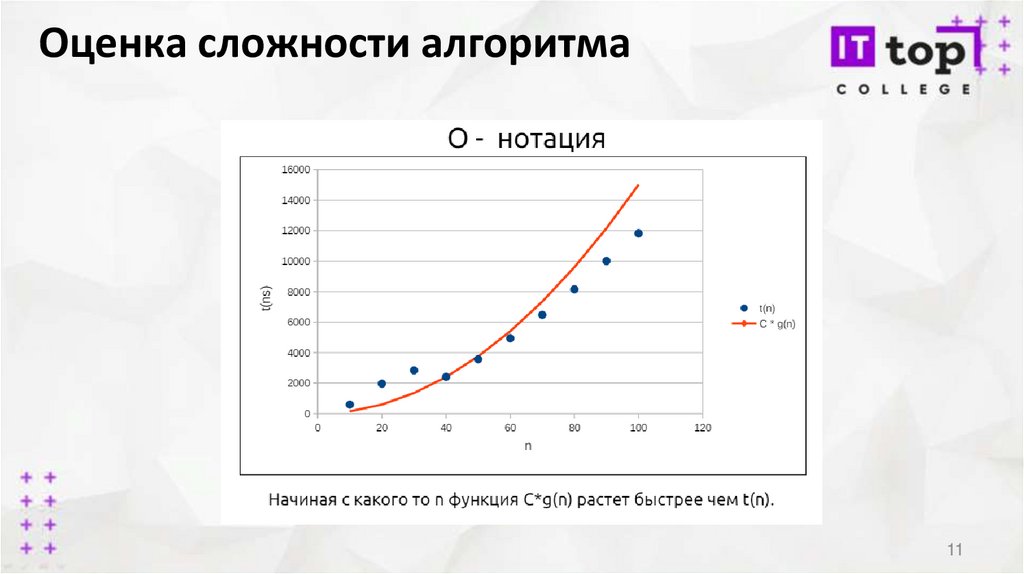
11.

Оценка сложности алгоритма
11

12.

Оценка сложности алгоритма
о-малое - это не просто "меньше". Когда пишут, что сложность алгоритма о(f), то хотят сказать, что с ростом параметра алгоритма сложность растёт
медленнее, чем f.
О-большое - это не просто "меньше или равно". Это означает, что где-то там,
на бесконечности, сложность алгоритма ведёт себя примерно как f. Если
совместить масштабы, то может быть даже совпадут. Ну или могут быть
выбросы соответствующего размера. В случае о-малого как масштаб ни
растягивай, всё равно мелко будет.
12

13.

Оценка сложности алгоритма
Пример:
s=0
for i in range(0, n):
for j in range(0, n):
s += i * j
В случае с o-малым нужно предъявить такую формулу, что сложность
алгоритма будет строго меньше этой формулы. Например сложность этого
алгоритма есть o(n^3) - он работает быстрее чем любой кубический
алгоритм. Или o(n^2.1), o(n^2+ε) для любого ε > 0, или o(n^2log(n)), или ещё
бесконечное число вариантов из которых нельзя выбрать один "самый
подходящий".
13

14.

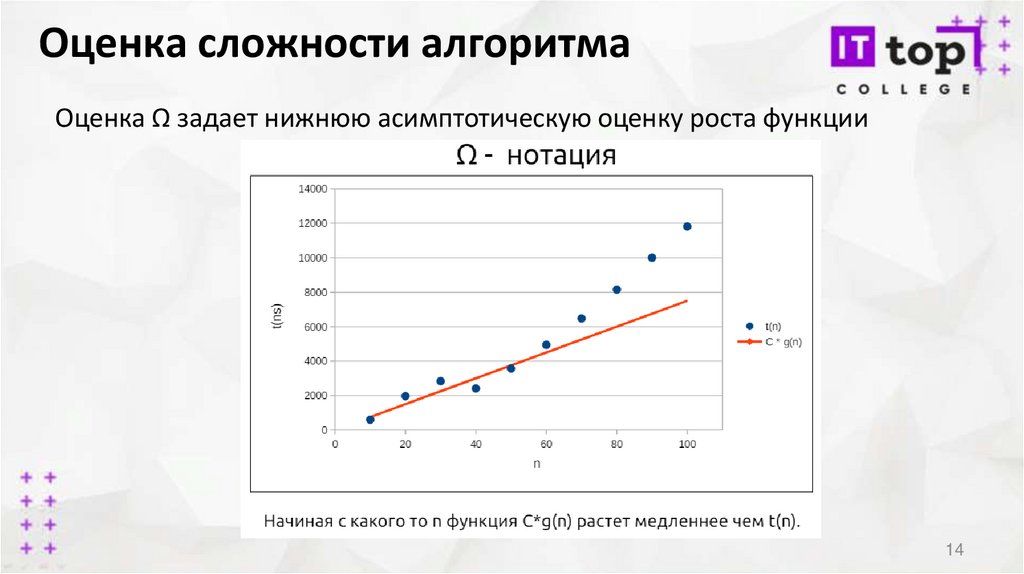
Оценка сложности алгоритма
Оценка Ω задает нижнюю асимптотическую оценку роста функции
14

15.

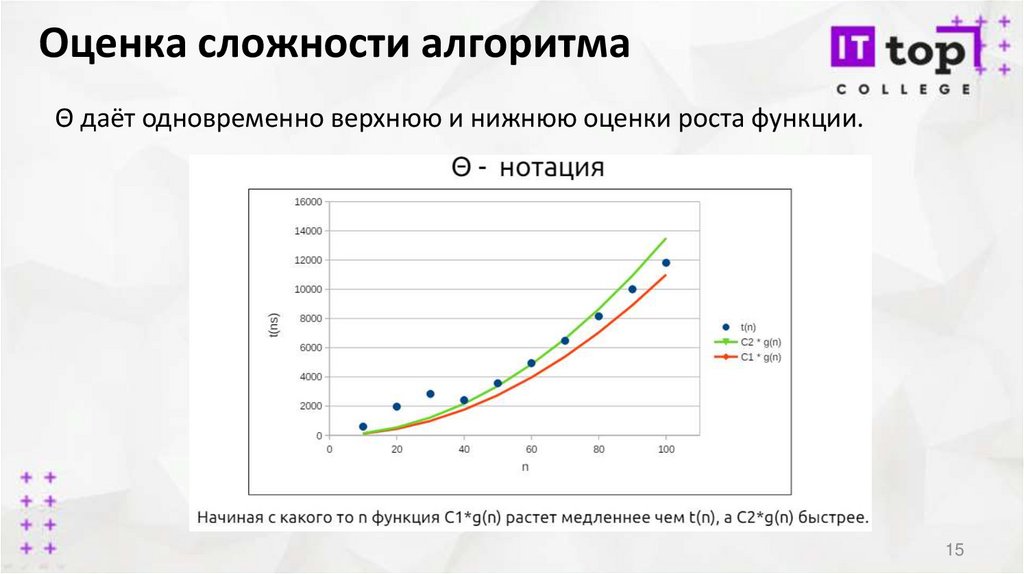
Оценка сложности алгоритма
Θ даёт одновременно верхнюю и нижнюю оценки роста функции.
15

16.

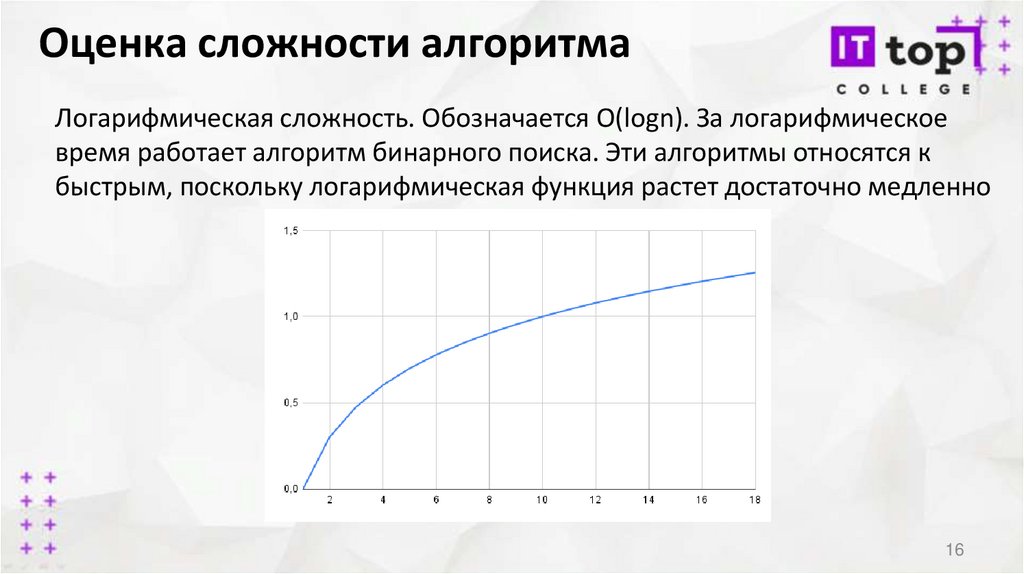
Оценка сложности алгоритма
Логарифмическая сложность. Обозначается О(logn). За логарифмическое
время работает алгоритм бинарного поиска. Эти алгоритмы относятся к
быстрым, поскольку логарифмическая функция растет достаточно медленно
16

17.

Оценка сложности алгоритма
Удвоение переменной цикла делает его логарифмическим по сложности. В
таких случаях для оценки сложности помогают основные свойства
логарифмов.
1) При смене основания добавляется константный множитель:
log