Основы теории Максвелла для электромагнитного поля

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной физики и химии
Основы теории Максвелла для
электромагнитного поля
Рогожина Татьяна Сергеевна
к.ф.-м.н., доцент

2.

1. Вихревое электрическое поле
2. Ток смещения
3. Уравнения Максвелла для электромагнитного
поля в интегральной форме
4. Свойства векторных полей
5. Уравнения Максвелла для электромагнитного
поля в дифференциальной форме
6. Дифференциальное уравнение электромагнитной
волны
7. Энергия и импульс электромагнитной волны
Максвелл Джеймс Клерк (1831—1879) – британский физик шотландского происхождения, специалист в области механики,
математики и оптики. Основоположник статистической физики и классической электродинамики. Автор закона распределения
молекул по скоростям, названный в его честь “распределением Максвелла”. Опубликовав в 1865 году «Динамическую теорию
электромагнитного поля», Максвелл продемонстрировал, что электрические и магнитные поля распространяются в пространстве в
виде волн, движущихся со скоростью света. Он предположил, что свет - это колебание в той же среде, которое является причиной
электрических и магнитных явлений. Объединение световых и электрических явлений привело к его предсказанию существования
радиоволн.

3.

1. Вихревое электрическое поле
i
d
dt следует, что любое изменение сцепленного с
Из закона Фарадея
контуром потока магнитной индукции приводит к возникновению
электродвижущей силы индукции, вследствие чего и появляется индукционный
ток. Следовательно возникновение ЭДС электромагнитной индукции возможно
и в неподвижном контуре, находящемся в переменном магнитном поле. Однако
ЭДС в любой цепи возникает только тогда, когда на носители тока действуют
сторонние силы – т.е. силы неэлектростатического происхождения. Опыт
показывает, что эти сторонние силы не связаны ни с тепловыми, ни с
химическими процессами в контуре, не вызваны силами Лоренца, т.к. силы
Лоренца действуют на движущиеся заряды, а эти неизвестные силы сами
заставляют частицы двигаться.
Джеймс Максвелл высказал гипотезу, что всякое переменное магнитное
поле возбуждает в окружающем пространстве электрическое поле, которое и
является причиной возникновения индукционного тока в контуре. Согласно
представлениям
Максвелла
контур
играет
лишь
роль
прибора
обнаруживающего это поле.

4.

Известно, что ЭДС индукции равна циркуляции вектора E по контуру
El dl
L
Гипотеза Максвелла гласит, что изменяющееся во времени магнитное поле порождает
электрическое поле, EB циркуляция которого:
d
L EB dl L EBl dl dt
где E Bl – проекция вектора EB на направление dl
Поставив в это выражение
получим
d
EB dl dt BdS
L
S

5.

Считая поверхность интегрирования S, образованную неподвижным контуром L, неподвижной, операции
дифференцирования и интегрирования можно поменять местами:
B
EB dl t dS
L
S
(символ частной производной подчеркивает тот факт, что интеграл
является функцией только от
времени).
Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю:
EQ dl EQl dl 0
Сравнивая выражения
B
EB dl t dS
L
S
E dl EQl dl 0
и Q
L
L
L
L
видим, что между рассматриваемыми полями
имеется принципиальное различие: циркуляция вектора
в отличие от циркуляции вектора
не равна пулю. Следовательно, электрическое поле
возбуждаемое
магнитным, как и само магнитное поле является вихревым.

6.

2. Ток смещения
Рассмотрим цепь переменного тока, содержащую конденсатор. Между обкладками заряжающегося и
разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу,
через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.
Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. По
Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле,
как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда
можно утверждать, что токи проводимости I и смещения Iсм равны.

7.

Ток проводимости вблизи обкладок конденсатора:
I
dQ d
d
dD
dS dS dS
dt dt S
S dt
S dt
(поверхностная плотность заряда на обкладках равна электрическому смещению D в конденсаторе.
Подынтегральное выражение в можно рассматривать как частный случай скалярного произведения
Подынтегральное выражение можно рассматривать как частный случай скалярного произведения
когда
D
t
и
dS
взаимно параллельны. Поэтому для общего случая можно записать
dD
dS .
S dt
I
jсмещ
Это выражение было названо Максвеллом плотностью тока смещения.
D
t
D
dS
t

8.

9.

10.

Из всех физических свойств, присущих току проводимости, Максвелл приписал току
смещения лишь одно — способность создавать в окружающем пространстве магнитное поле.
В диэлектриках ток смещения состоит из двух слагаемых.
D 0 E P
где - Е напряженность электростатического поля, а Р - поляризованность, тогда плотность тока смещения
E P
jсмещ 0
,
t t
где —
0
E
плотность тока смещения в вакууме;
t
P
— плотность тока поляризации — тока,
t
обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в
неполярных молекулах или поворот диполей в полярных молекулах).

11.

Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по
своей природе не отличаются от токов проводимости. Однако то, что и другая часть плотности
E
тока смещения
не связана с движением зарядов, а обусловлена только изменением
0
t
электрического поля во времени, но также возбуждает магнитное поле, является принципиально
новым утверждением Максвелла.
Даже в вакууме всякое изменение во времени электрического поля приводит к возникновению в
окружающем пространстве магнитного поля. Следует отметить, что название «ток смещения» является
условным, а точнее исторически сложившимся, так как ток смещения по своей сути — это изменяющееся
со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или
диэлектриках, но и внутри проводников, по которым проходит переменный ток. Однако в данном случае он
пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено
экспериментально А.А.Эйхенвальдом, изучавшим магнитное поле тока поляризации, который, как следует
является частью тока смещения.
E P
jсмещ 0
.
t t

12.

Максвелл ввел понятие полного тока, равного сумме токов проводимости (а также
конвекционных токов) и смещения. Плотность полного тока
D
jполн j
.
t
Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рассмотрению
замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т.е. на концах проводника
обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется
ток смещения, который замыкает ток проводимости.
Максвелл обобщил теорему о циркуляции вектора
H
Hdl I
L
введя в ее правую часть полный ток I полн jполн dS сквозь поверхность S, ограниченную замкнутым контуром L.
S

13.

Тогда обобщенная теорема о циркуляции вектора
H
запишется в виде:
D
Hdl j t dS
L
S
Это выражение справедливо всегда, что подтверждается полным соответствием теории и опыта.

14.

3. Уравнения Максвелла для электромагнитного поля в интегральной форме
Введение Максвеллом понятия тока смещения привело его к завершению созданной им
макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только
объяснить электрические и магнитные явления, но и предсказать новые, существование которых
было впоследствии подтверждено. В основе теории Максвелла лежат рассмотренные выше два
уравнения и теорема Гаусса для электрического и магнитного полей:
1. Электрическое поле может быть как потенциальным ( E ), так и вихревым ( EB ), поэтому
Q
напряженность суммарного поля
циркуляция вектора
E EQ EB . Так как циркуляция вектора EQ равна нулю, а
EB определяется выражением
B
L EB dl S t dS

15.

то циркуляция вектора напряженности суммарного поля
B
Edl t dS
L
S
Это уравнение показывает, что источниками электрического поля могут быть не
только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора
H
D
Hdl j t dS
L
S
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами
(электрическими токами), либо переменными электрическими полями.

16.

3. Теорема Гаусса для поля
D
DdS Q
S
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то
формула запишется в виде:
DdS dV
S
V
Уравнение показывает, что линии вектора D могут начинаться и заканчиваться на зарядах.

17.

4. Теорема Гаусса для поля
B
BdS 0
S
Это уравнение отражает то свойство магнитного поля, что его линии замкнуты и магнитных
зарядов не существует.

18.

Полная система уравнений Максвелла в интегральной форме.
B
Edl t dS
L
S
– Закон электромагнитной индукции Фарадея.
DdS dV
– Теорема Гаусса для электрического поля.
S
V
D
Hdl j t dS
L
S
– Закон полного тока.
BdS 0
– Теорема Гаусса для магнитного поля
S

19.

Величины, входящие в левые части уравнений Максвелла, не являются независимыми, и между ними
существует связь, которая для изотропных несегнетоэлектрических и неферромагнитных сред будет
иметь вид:
D 0 E
B 0 H
j E

20.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть
либо электрические заряды, либо изменяющиеся во времени магнитные поля, а
магнитные поля могут возбуждаться либо движущимися электрическими зарядами
(электрическими токами), либо переменными электрическими полями. Уравнения
Максвелла не симметричны относительно электрического и магнитного полей. Это
связано с тем, что в природе существуют электрические заряды, но отсутствуют
магнитные.
Если поля не изменяются с течением времени (они называются стационарными полями), то уравнения Максвелла в
пустом пространстве (вакууме) примут вид:
Edl 0
L
DdS Q
S
Hdl I
L
BdS 0
S
т.е. источниками электрического поля в данном случае
являются только электрические заряды, а источниками
магнитного — только токи проводимости. В данном случае
электрические и магнитные поля независимы друг от друга,
что
и
позволяет
изучать
электрическое и магнитное поля.
отдельно
постоянные

21.

4. Описание свойств векторных полей
Поток вектора через некоторую поверхность и циркуляция вектора по заданному контуру
позволяют судить о характере векторного поля. Однако эти величины дают среднюю
характеристику поля в пределах объёма, охватываемого поверхностью, через которую
определяется поток, или в окрестности контура по которому берется циркуляция. Уменьшая
размеры поверхности или контура (стягивая их в точку), можно прийти к величинам, которые
будут характеризовать векторное поле в данной точке. Для того, чтобы ввести эти величины нам
придётся глубоко вникнуть в смысл понятий дивергенции и ротора.

22.

Диверге́нция —дифференциальный оператор, отображающий векторное поле на
скалярное
(то
есть,
в
результате
применения
к
векторному
полю
операции
дифференцирования получается скалярное поле), который определяет (для каждой
точки), «насколько расходится входящее и исходящее из малой окрестности данной точки
поле», точнее, насколько расходятся входящий и исходящий потоки.
Определение дивергенции выглядит так:
A
divA lim
V 0 V
в пределе при стремлении объёма к нулю, т.е. при стягивании объёма к точке, выражение
дает истинную удельную мощность источников в точке, которую и называют дивергенцией
вектора А.
В трёхмерном декартовом пространстве дивергенция будет определяться выражением
Ax Ay Az
divA A
x
y
z

23.

С точки зрения физики дивергенция векторного поля является показателем того, в какой
степени данная точка пространства (точнее достаточно малая окрестность точки) является
источником или стоком этого поля:
divА>0
divА<0
divА=0
-
точка поля является источником;
-
точка поля является стоком
- стоков и источников нет, либо они компенсируют друг друга.
Зная дивергенцию вектора в каждой точке пространства, можно вычислить поток этого вектора через любую
поверхность конечных размеров с помощью теоремы Остроградского-Гаусса.
AdS divAdV
S
V

24.

Ротор — это векторный дифференциальный оператор над векторным полем.
Ротор поля A обозначается символом rotA, определяется векторным произведением
rotA A
где — векторный дифференциальный оператор набла.
i
j k
x
y
z
Результат действия этого оператора на конкретное векторное поле А представляет собой новое
векторное поле.
Физически поле ротора А, т.е. длина и направление вектора rot А в каждой точке
пространства, характеризует в некотором смысле вращательную составляющую поля А
соответственно в каждой точке. Или по-другому показывает, насколько и в каком направлении
закручено поле в каждой точке.

25.

Математически ротор векторного поля А — есть вектор, проекция которого rotnА на
каждое направление n равна пределу отношения циркуляции векторного поля по замкнутому
контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной к этому
направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама
площадка стягивается в точку:
Adr
rotAn lim L
S 0
S
В теории поля между циркуляцией векторного поля и его ротором установлена связь, доказанная
теоремой Стокса, которая формулируется следующим образом: циркуляция вектора силы поля по
замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого
вектора через поверхность, ограниченную этой кривой, в направлении нормали.
Adl rotA n dS
L
S

26.

5. Уравнения Максвелла в дифференциальной форме
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса:
Adl rotAdS
L
S
AdS divAdV
S
V
можно представить полную систему уравнений Максвелла в дифференциальной форме
(характеризующих поле в каждой точке пространства):

27.

Cистема уравнений Максвелла в дифференциальной форме
B
rotE
t
divD
D
rotH j
t
divB 0

28.

Дифференциальные операторы ротор (rot) и дивергенция (div) можно
рассчитать по формулам:
E x E y E z
divE E
x
y
z
i
rotE E
x
Ex
j
y
Ey
k
E z E y i E z E x j E y E x k
z y
z x
z x
y
Ez

29.

Спроецировав уравнение
B
rotE ;
t
на координатные оси, получим вместо векторного уравнения три скалярных.
Bx
Ez E y
y
z
t
.
By
Ex Ez
z
x
t
E y
Ex
Bz
x
y
t

30.

Спроецировав уравнение
D
rotH j
;
t
на координатные оси, получим вместо векторного уравнения следующие три скалярных.
Dx
H z H y
jx
y
z
t
.
Dy
H x H z
jy
z
x
t
H y
H x
Dz
jz
x
y
t

31.

Уравнение
divD
можно переписать в виде:
Dx Dy Dz
x
y
z
Уравнение
divB 0
можно переписать в виде:
Bx By Bz
0
x
y
z

32.

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений
Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются
поверхности разрыва — поверхности, на которых свойства среды или полей меняются
скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в
пространстве
и
времени
изменяются
непрерывно.
Чтобы
достичь
математической
эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют
граничными условиями, которым должно удовлетворять электромагнитное поле на границе
раздела двух сред.
Dn1 Dn 2 ;
E 1 E 2 ;
Bn1 Bn 2 ;
H 1 H 2

33.

Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в
покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в
механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с
порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым
им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют
единое электромагнитное поле.
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, не
только смогла объяснить уже известные экспериментальные факты, что также является важным ее
следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось
существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование
электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве
с конечной скоростью.
В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля
(не связанного с зарядами и токами) в вакууме равна скорости света с = 3 108 м/с.

34.

Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к
созданию электромагнитной теории света, согласно которой свет представляет собой также
электромагнитные волны.
Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894),
доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями
Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена. К
электромагнитному полю применим принцип относительности Эйнштейна, так как факт
распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой
скоростью с не совместим с принципом относительности Галилея. Согласно принципу
относительности Эйнштейна, механические, оптические и электромагнитные явления во всех
инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми
уравнениями.

35.

36.

Таким образом, теория Максвелла, ее экспериментальное подтверждение, а
также принцип относительности Эйнштейна приводят к единой теории
электрических,
магнитных
и
оптических
представлении об электромагнитном поле.
явлений,
базирующейся
на

37.

6. Дифференциальное уравнение электромагнитной волны
Существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в
пространстве с конечной скоростью, — вытекает из уравнения Максвелла. Решающую роль для
утверждения максвелловской теории сыграли опыты Генриха Герца (1888), согласно которым
электрические и магнитные поля действительно распространяются в виде волн, поведение которых
полностью описывается уравнениями Максвелла. Источником электромагнитных волн в действительности
может быть любой электрический колебательный контур или проводник, по которому течет переменный
электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве
переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако
излучающая способность источника определяется его формой, размерами и частотой колебаний.
Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором создается
переменное электромагнитное поле. Поэтому для получения электромагнитных волн непригодны закрытые
колебательные контуры, так как в них электрическое поле сосредоточено между обкладками конденсатора,
а магнитное — внутри катушки индуктивности.

38.

Г. Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а
также раздвигая их, совершил переход от закрытого колебательного контура к открытому
колебательному контуру (вибратору Герца), представляющему собой два стрежня, разделенных
искровым промежутком.
Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри
конденсатора, то в открытом оно заполняет окружающее контур пространство, что существенно повышает
интенсивность электромагнитного излучения. Колебания в такой системе поддерживаются за счет источника
ЭДС, подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы
увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

39.

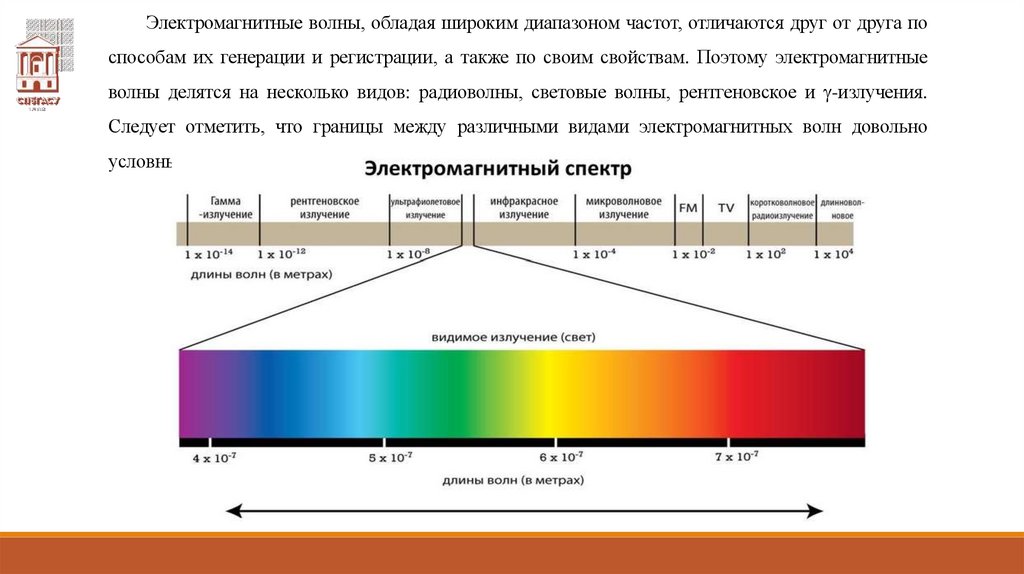
Электромагнитные волны, обладая широким диапазоном частот, отличаются друг от друга по
способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные
волны делятся на несколько видов: радиоволны, световые волны, рентгеновское и -излучения.
Следует отметить, что границы между различными видами электромагнитных волн довольно
условны.

40.

Из уравнений Максвелла следует, что для однородной и изотропной среды вдали от зарядов
и токов, создающих электромагнитное поле, векторы напряженностей Е и Н переменного
электромагнитного поля удовлетворяют волновому уравнению типа
1 E
E 2 2
v t
2
2
2
2
2 2 2
x
y
z
1 H
H 2 2
v t
2
- оператор Лапласа, v – фазовая скорость.

41.

Всякая
функция,
удовлетворяющая
этим
уравнениям,
описывает
некоторую волну. Следовательно, электромагнитные поля действительно
существуют в виде электромагнитных волн.
Фазовая скорость электромагнитных волн определяется выражением
v
1
1
0
0
1
0 0
n
c
1
0 0
3 108 м / с
с
с
n
1
1

42.

В вакууме (при =1 и =1) скорость распространения электромагнитных волн совпадает со
скоростью с. В веществе > 1, поэтому скорость распространения электромагнитных волн в
веществе всегда меньше, чем в вакууме. При вычислении скорости распространения
электромагнитного поля по вышеприведенной формуле получается результат, достаточно хорошо
совпадающий с экспериментальными данными, если учитывать зависимость и от частоты.
Совпадение же размерного коэффициента со скоростью распространения света в вакууме
указывает
на
глубокую
связь
между
электромагнитными
и
оптическими
явлениями,
позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет
представляет собой электромагнитные волны.

43.

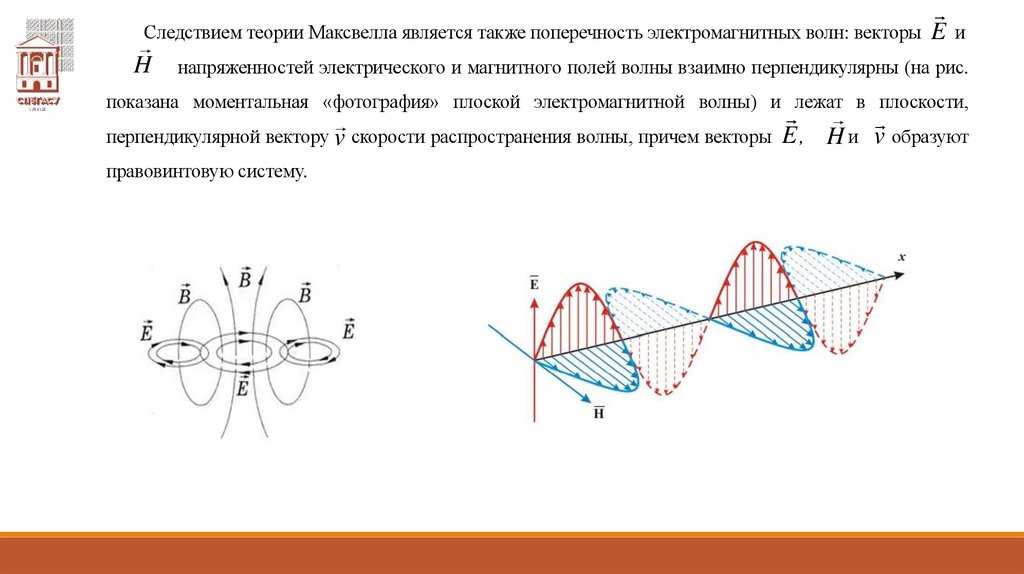
Следствием теории Максвелла является также поперечность электромагнитных волн: векторы E и
H
напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис.
показана моментальная «фотография» плоской электромагнитной волны) и лежат в плоскости,
перпендикулярной вектору v скорости распространения волны, причем векторы E ,
правовинтовую систему.
H и v образуют

44.

Из уравнений Максвелла следует также, что в электромагнитной волне
векторы
E
и
H
всегда колеблются в одинаковых фазах, причем
мгновенные значения в любой точке связаны соотношением
0 E 0 H .
Следовательно, E и H одновременно достигают максимума, одновременно обращаются в нуль и т. д.
От уравнений
1 2E
E 2 2 ,
v t
1 2H
H 2 2 ,
v t
можно перейти к уравнениям
2 E
1 2 E
2
,
2
2
x
v t
Векторы
E и H
2 H
1 2 H
2 2
2
x
v t
направлены вдоль взаимно перпендикулярных осей у и z.

45.

Этим уравнениям удовлетворяют, в частности, плоские монохроматические
электромагнитные волны (электромагнитные волны одной строго определенной
частоты), описываемые уравнениями
E y E0 cos t kx ,
H z H 0 cos t kx ,

46.

7. Энергия и импульс электромагнитной волны
Объемная плотность энергии w электромагнитной волны складывается из
объемных плотностей wэл электрического и wм магнитного полей:
w wэл wм
Учитывая связь векторов
0 E 2
2
0 H 2
2
E и H , получим, что плотности энергии электрического и магнитного
полей в каждый момент времени одинаковы, т. е. wэл= wМ
Следовательно, плотность энергии электромагнитного поля можно представить в виде:
w 2wэл 0 0 EH

47.

Если умножить плотность энергии W на скорость электромагнитной волны в среде:
c
v
,
то получим модуль плотности потока энергии:
1
S w v EH v EH
v

48.

Следовательно, вектор плотности потока электромагнитной энергии имеет вид:
S w v E H [ EH ]
Вектор
S
называют вектором Умова – Пойнтинга, он показывает
направление распространения электромагнитной волны, а его модуль равен
энергии, переносимой электромагнитной волной за единицу времени через
единичную площадку, перпендикулярную направлению распространения волны.

49.

Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены
опытами Г. Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела
давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны
заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного
поля волны действию сил Лоренца. Однако значение этого давления ничтожно мало. Можно оценить, что
при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно
поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших
классическими, П. Н. Лебедев в 1899 г. доказал существование светового давления на твердые тела, а в 1910
г. — на газы. Опыты Петра Николаевича Лебедева имели огромное значение для утверждения выводов
теории Максвелла о том, что свет представляет собой электромагнитные волны. Существование давления
электромагнитных волн приводит к выводу о том, что им присущ механический импульс.
Электромагнитная волна, несущая энергию W, обладает импульсом
p
W
c

50.

Санкт-Петербургский государственный
архитектурно-строительный университет
Кафедра строительной физики и химии
https://youtu.be/kbkhg3BeOUI
волны 3 мин.
Авторы:
Рогожина Татьяна Сергеевна
-
Электромагнитные