Математика. Тема 23. Цилиндр

1.

Математика
Преподаватели:
Кормилицына Елена Анатольевна,
Федотова Екатерина Алексеевна

2.

Тема 23.
Цилиндр

3. План лекции

1. Понятие цилиндра.
2. Осевое сечение цилиндра.
3. Виды цилиндра.
4. Площадь и объём.

4.

5.

6.

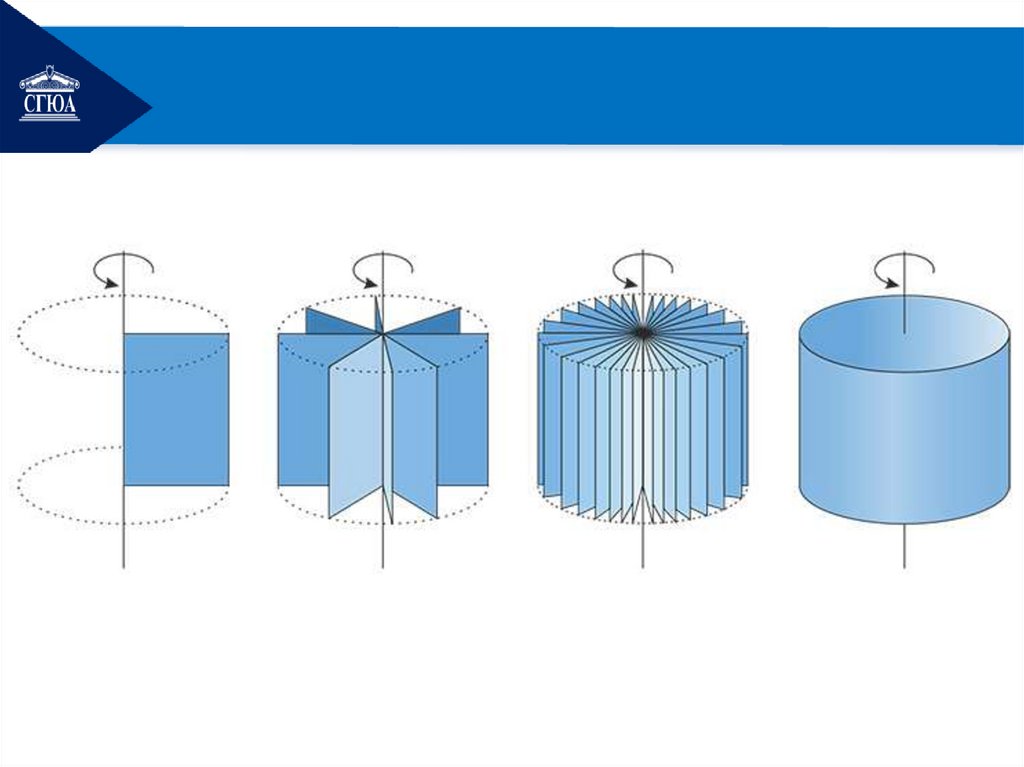
1.Понятие цилиндра
Опр. Цилиндром называется
геометрическое тело
вращения, которое
получается при вращении
прямоугольника вокруг его
стороны.

7.

8.

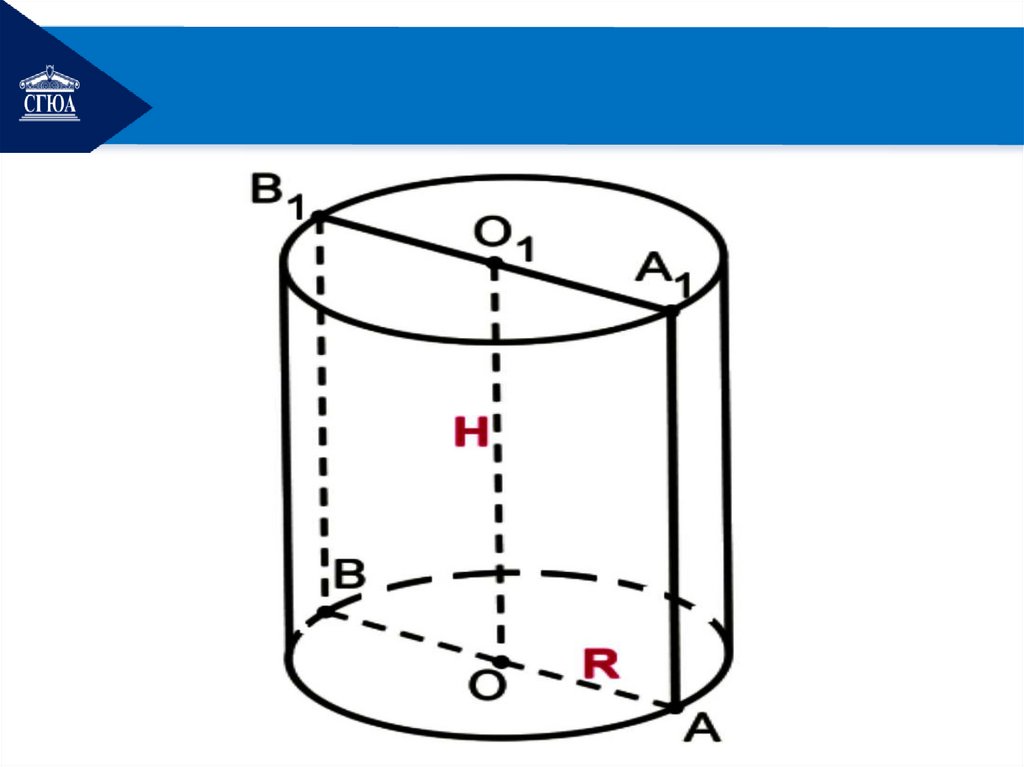
• Прямоугольник AOO A
1 1
вращается вокруг
стороны OO ;
1
• OO1 ось
симметрии цилиндра
и высота цилиндра;

9.

•AA образующая
1
цилиндра, длина
которой равна длине высоты
цилиндра, то есть ОО AA ;
1
1
•AO — радиус цилиндра, то
есть AO=R.

10.

Полученная цилиндрическая
поверхность
называется боковой
поверхностью цилиндра, а
круги – основаниями
цилиндра.

11.

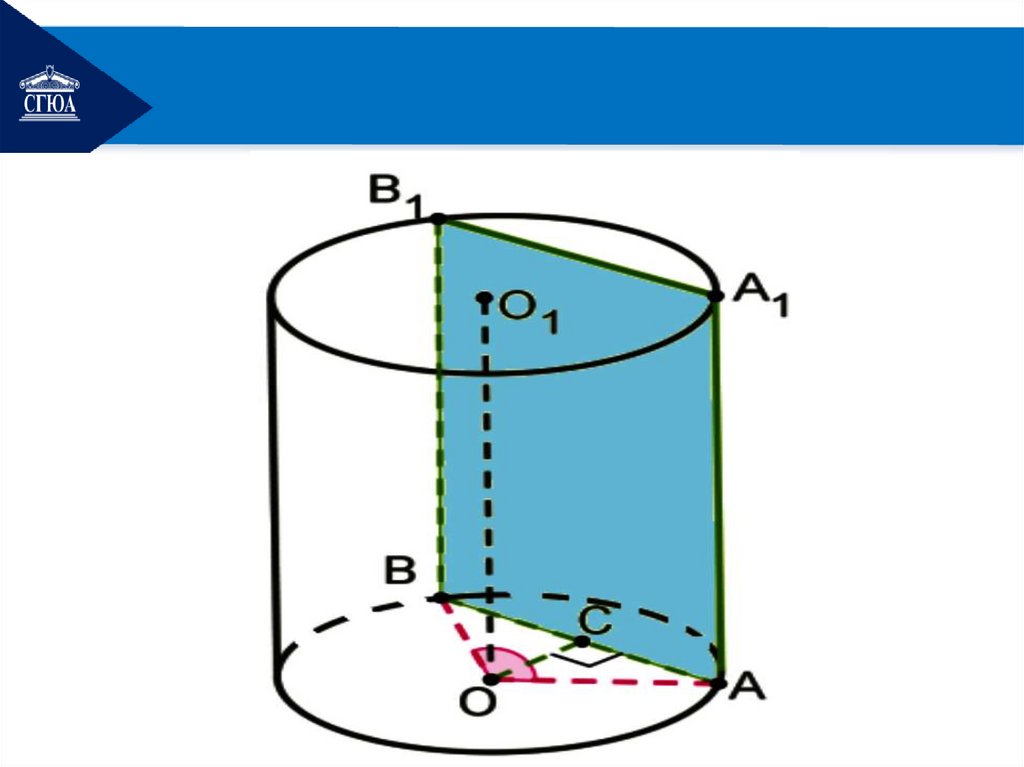
2. Осевое сечение.
Опр. Осевое сечение
цилиндра – это сечение
цилиндра плоскостью,
которая проходит через ось
цилиндра. Это сечение
является прямоугольником.

12.

При сечении цилиндра
плоскостью, параллельной
оси цилиндра (т. е.
перпендикулярной
основанию), также
получается прямоугольник.

13.

14.

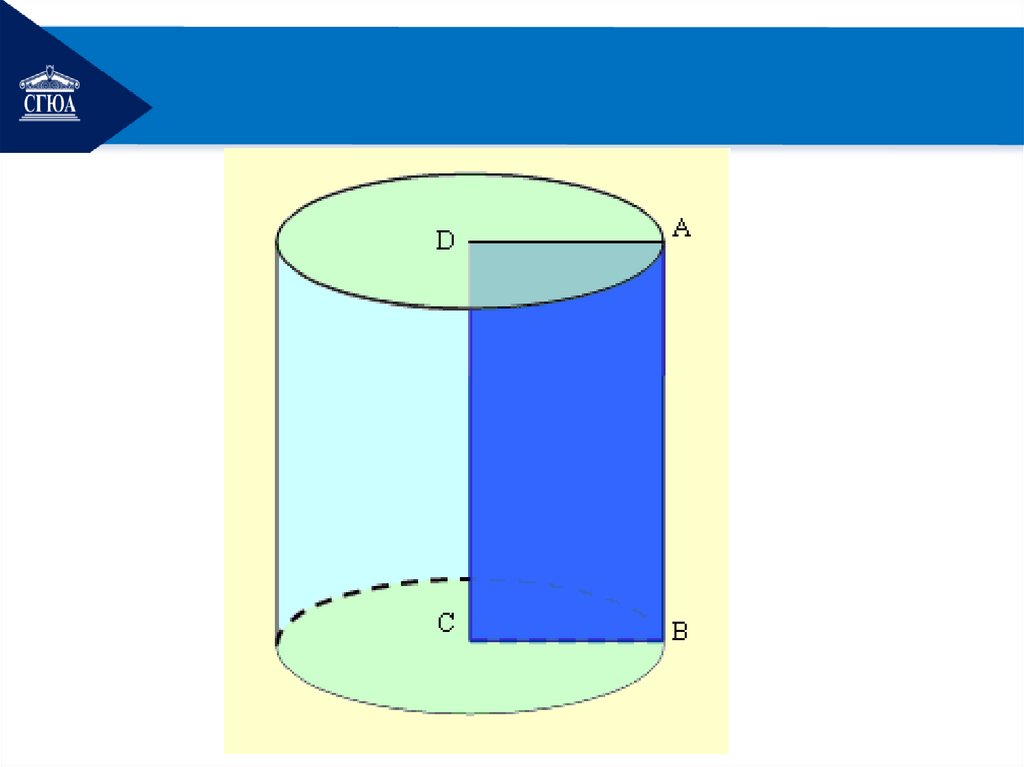
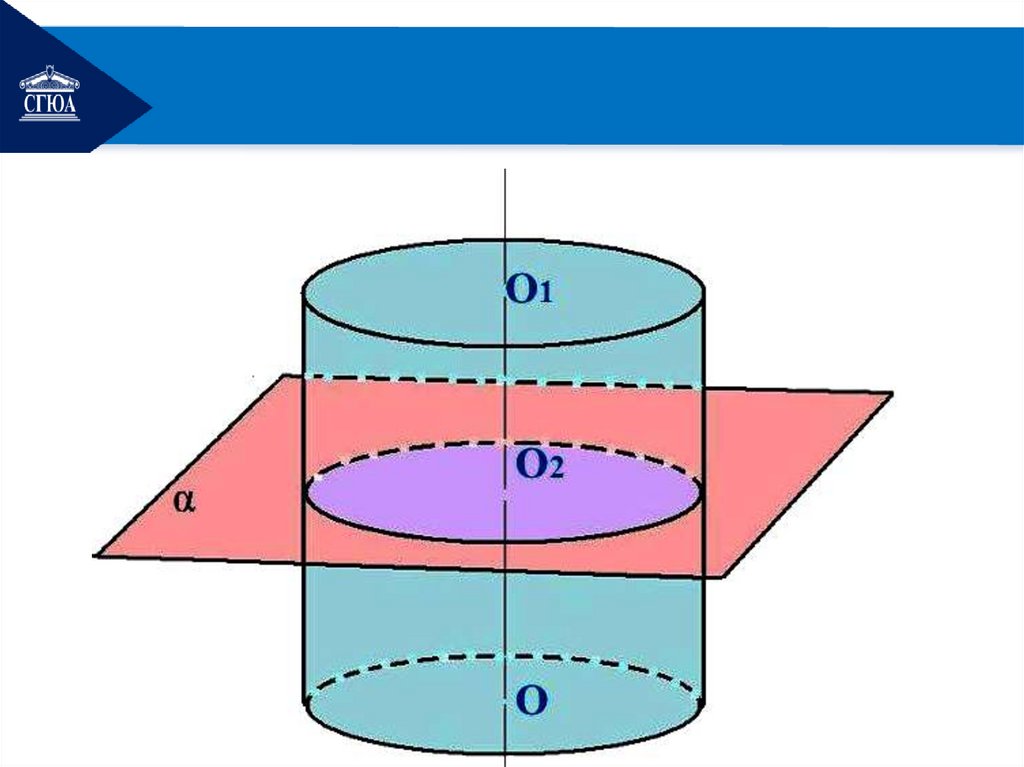
На рисунке изображён
цилиндр, пересечённый
плоскостью, которая
параллельна оси
цилиндра – OO .
1
ABB1 A1 прямоугольник.
OA=OB=R — радиусы.

15.

OC — расстояние от
оси цилиндра до плоскости
сечения.
При сечении цилиндра
плоскостью, параллельной
основанию, в сечении
получаем круг, равный
основаниям цилиндра.

16.

17.

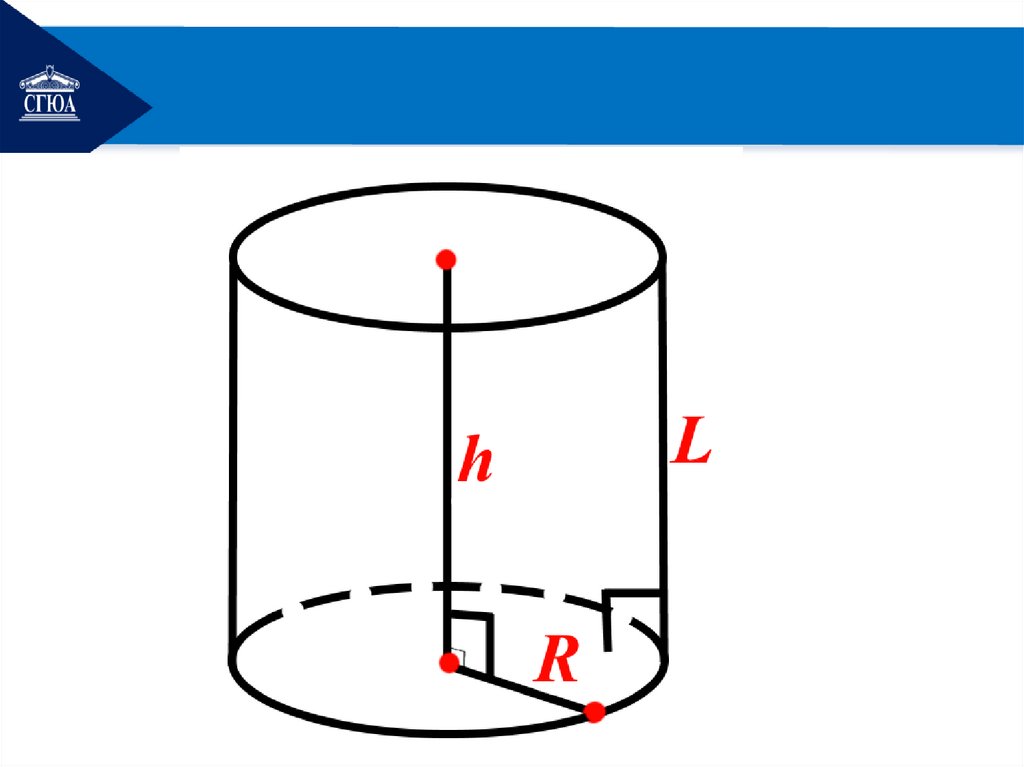
3. Виды цилиндра
Прямой круговой цилиндр.
Цилиндр называется прямым,
если его образующая
перпендикулярна основаниям.
Прямой круговой
цилиндр определяется радиусом
основания R и образующей L,
равной высоте H.

18.

19.

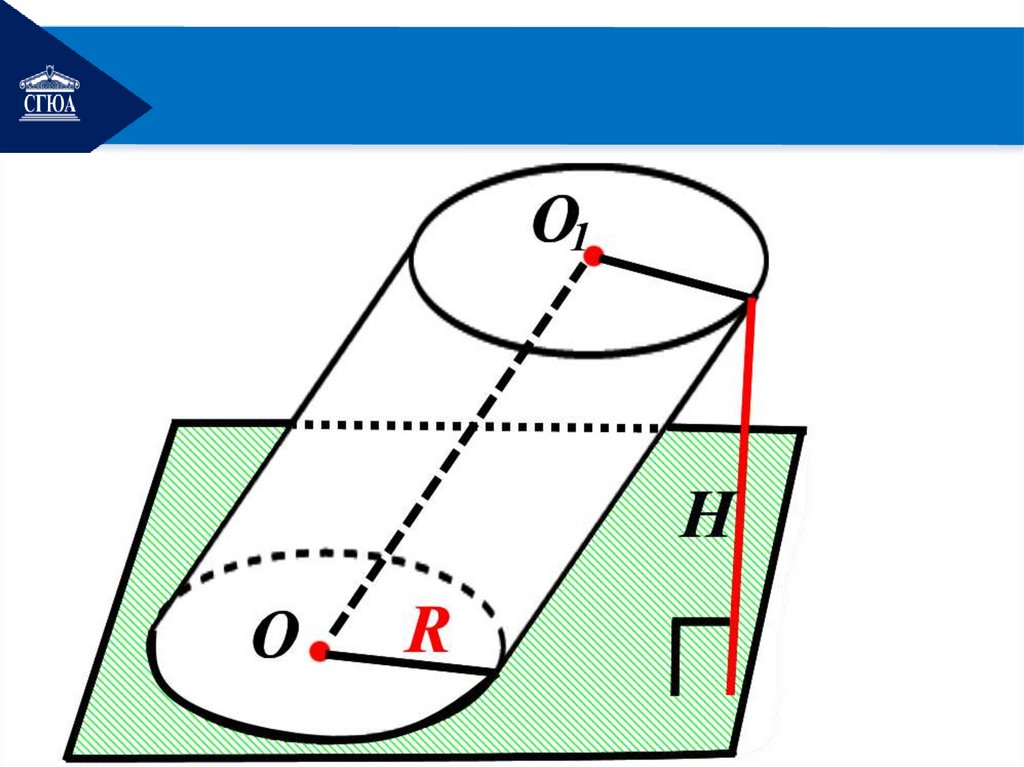
Наклонный цилиндр.
Цилиндр называется
наклонным, если его
образующие не
перпендикулярны основаниям
цилиндра, то есть образуют
угол не равный 90º .

20.

21.

4. Площадь и объём
Если представить, что боковая
цилиндрическая поверхность
разрезана по образующей
AA1
и развёрнута, получаем
прямоугольник.

22.

23.

Длину окружности основания
легко посчитать зная
определение числа π :
l
l
l 2 R
d
2R

24.

25.

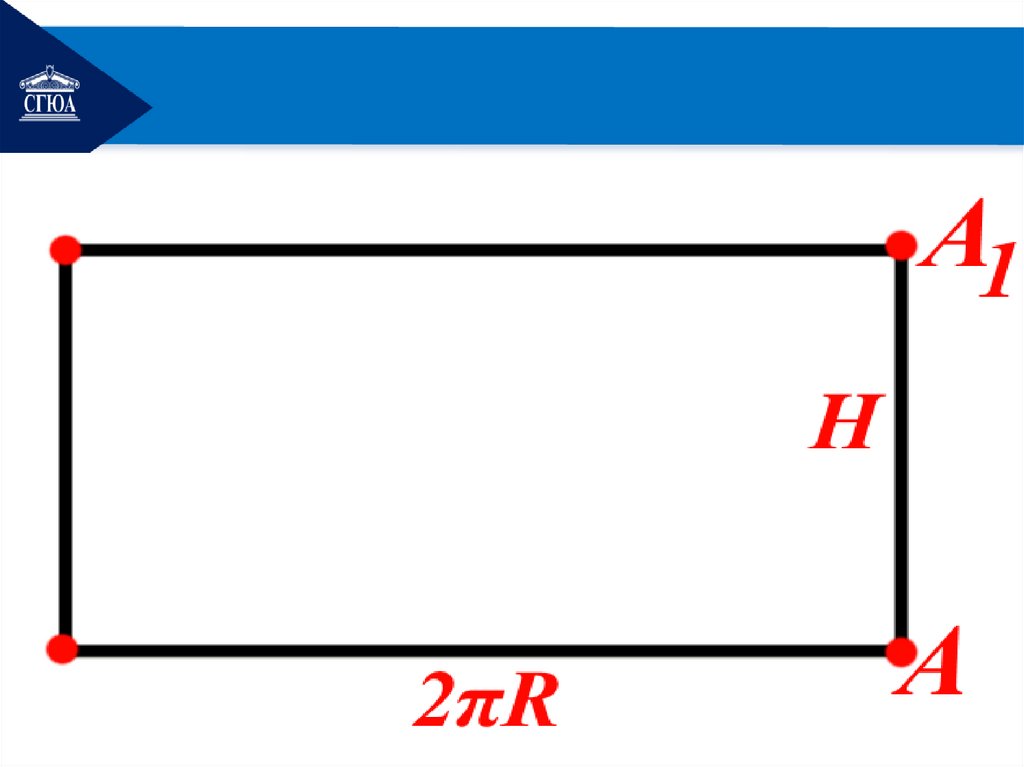
Сторона AA равна высоте H,
1
а другую сторону образует
развёрнутая окружность
основания длиной 2πR.
Так как развёртка —
прямоугольник, то площадь
легко вычислить использую
формулу площади
прямоугольника.

26.

Теорема(Площадь боковой
поверхности).Площадь
боковой поверхности
цилиндра вычисляется по
формуле:
Sбок 2 R H

27.

Основания цилиндра — два
круга. Площадь одного круга
2
равна
, следовательно
R
общая площадь двух кругов
2
будет равняться
2
R
.
Тогда справедлива теорема:

28.

29.

Теорема(Площадь полной
поверхности).Площадь полной
поверхности цилиндра
вычисляется по формуле:
S полн 2 R H 2 R
2

30.

Теорема(Объём цилиндра).
Объём цилиндра вычисляется
по формуле:
V R H
2