Похожие презентации:
Цилиндр
1.
Цилиндр2. Цилиндр
Определение цилиндра какгеометрического тела
Прямой цилиндр
Элементы цилиндра (поверхность,
высота, радиус, ось)
Определение цилиндра как тела
вращения
Свойства цилиндра
Сечения цилиндра плоскостями
Вписанная и описанная призма
Площадь цилиндра
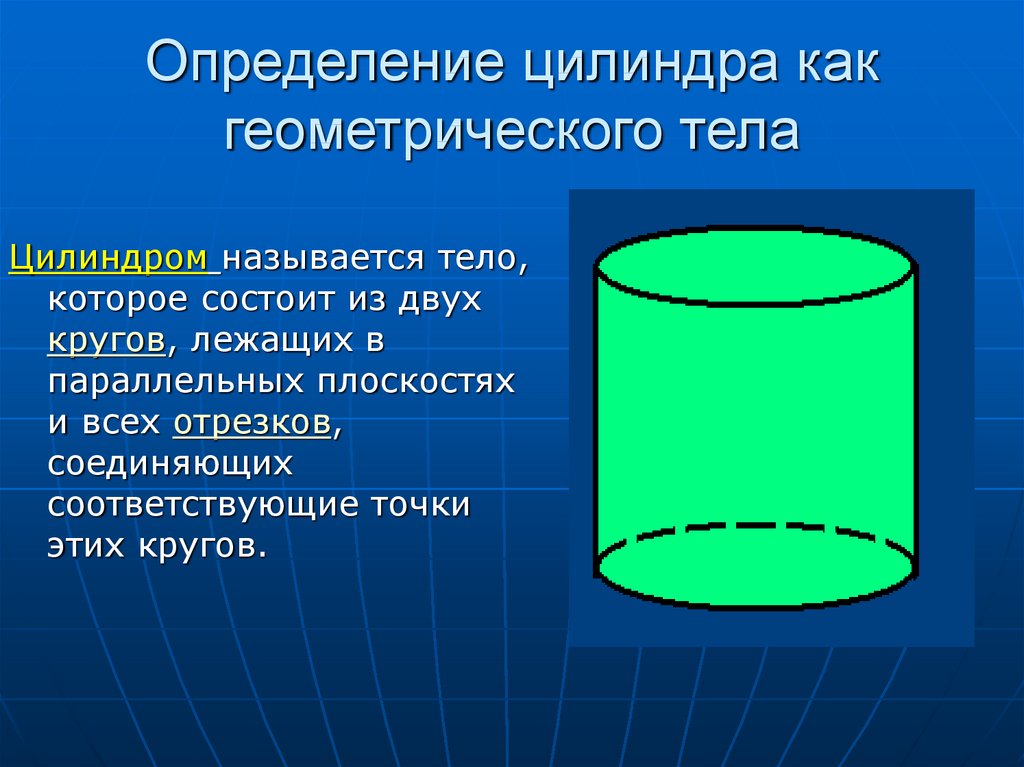
3. Определение цилиндра как геометрического тела
Цилиндром называется тело,которое состоит из двух
кругов, лежащих в
параллельных плоскостях
и всех отрезков,
соединяющих
соответствующие точки
этих кругов.
4.
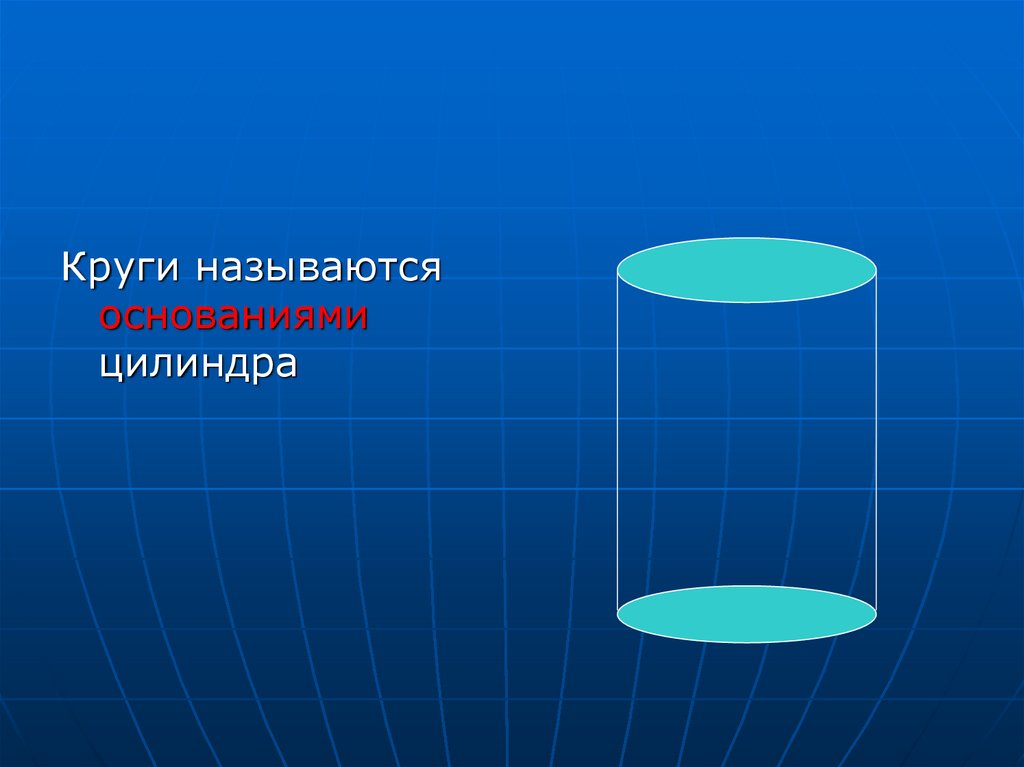
Круги называютсяоснованиями
цилиндра
5.
Отрезки,соединяющие
соответствующие
точки
окружностей
кругов
называются
образующими
цилиндра
6.
Цилиндр называется прямым, еслиего образующие перпендикулярны
плоскостям оснований.
7. Элементы цилиндра
Поверхность цилиндраВысота цилиндра
Ось цилиндра
Радиус цилиндра
8.
Поверхность цилиндра состоит изоснований и боковой поверхности.
Боковая поверхность составлена
из образующих.
9.
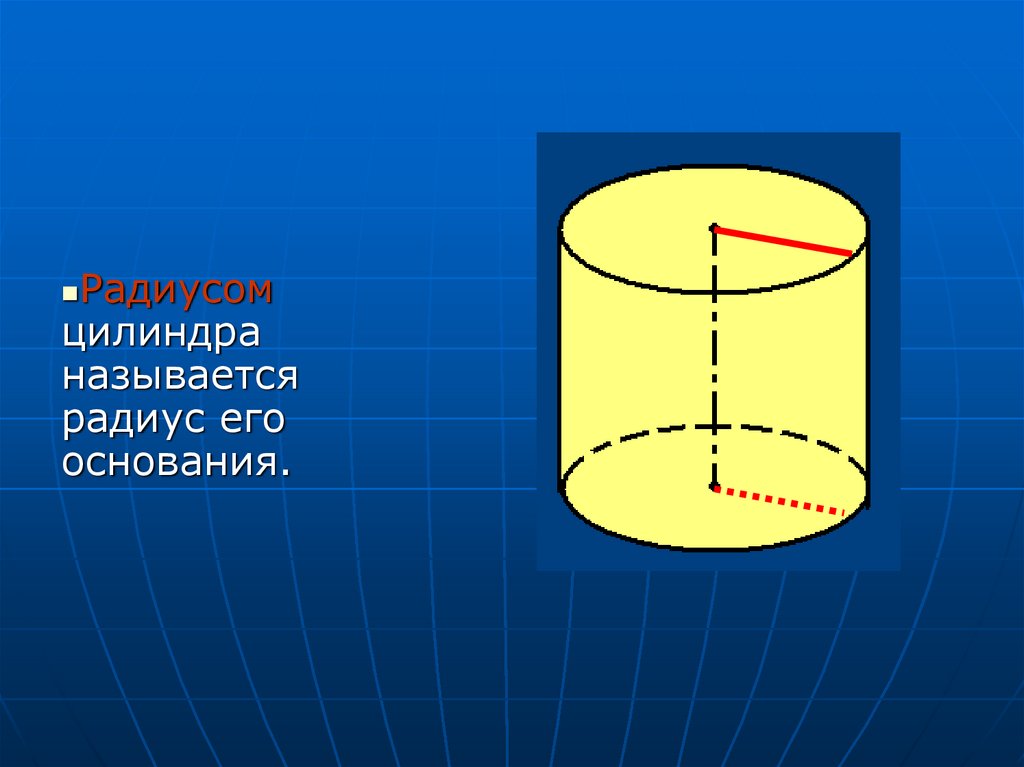
Радиусомцилиндра
называется
радиус его
основания.
10.
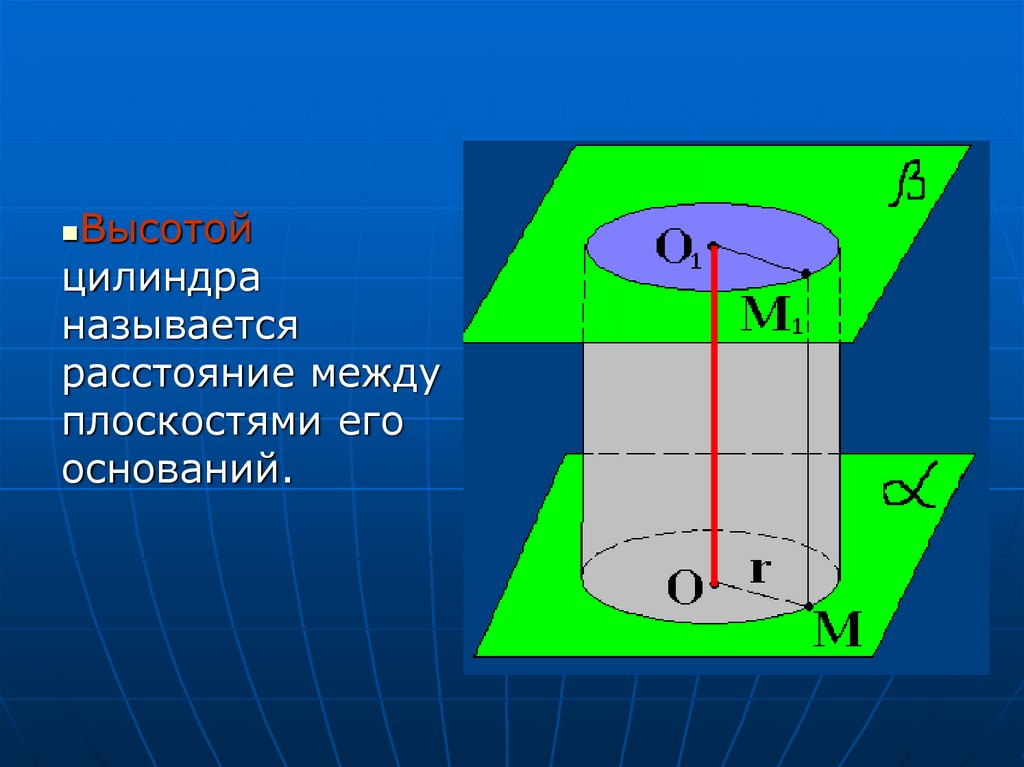
Высотойцилиндра
называется
расстояние между
плоскостями его
оснований.
11.
Осью цилиндраназывается
прямая,
проходящая
через центры
оснований. Она
параллельна
образующим.
12. Цилиндр как тело вращения
Цилиндр может бытьполучен вращением
прямоугольника
вокруг одной из его
сторон.
13.
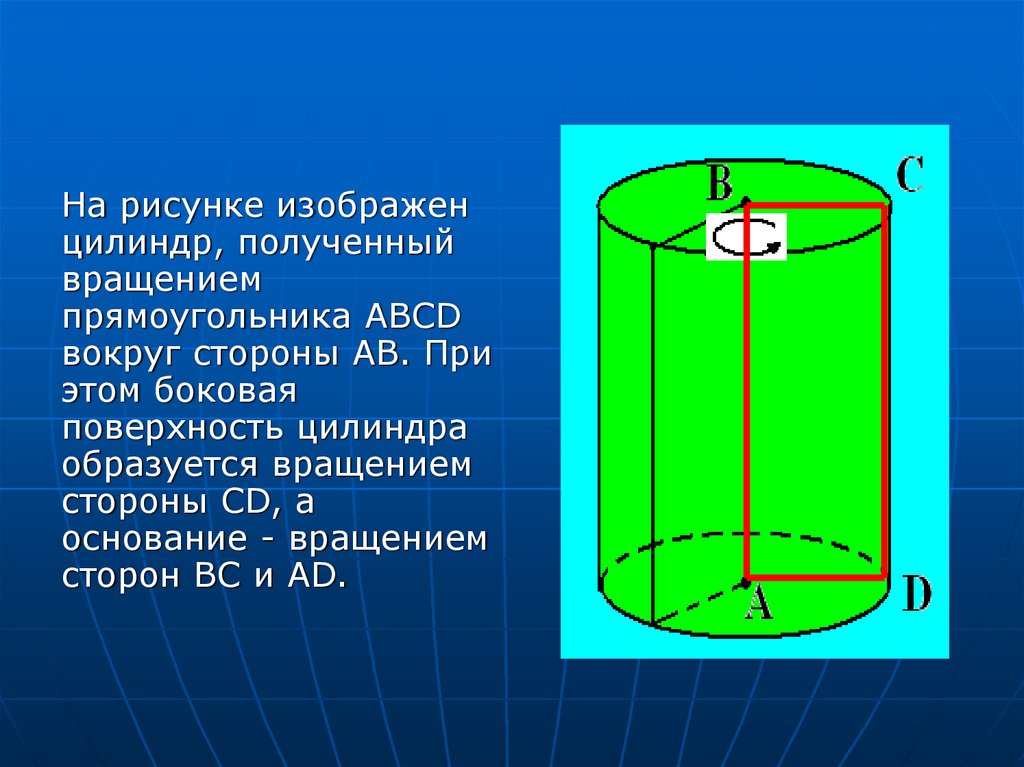
На рисунке изображенцилиндр, полученный
вращением
прямоугольника ABCD
вокруг стороны AB. При
этом боковая
поверхность цилиндра
образуется вращением
стороны CD, а
основание - вращением
сторон BC и AD.
14. Свойства цилиндра
Основания цилиндра равны.Основания цилиндра лежат в
параллельных плоскостях.
Образующие цилиндра
параллельны и равны
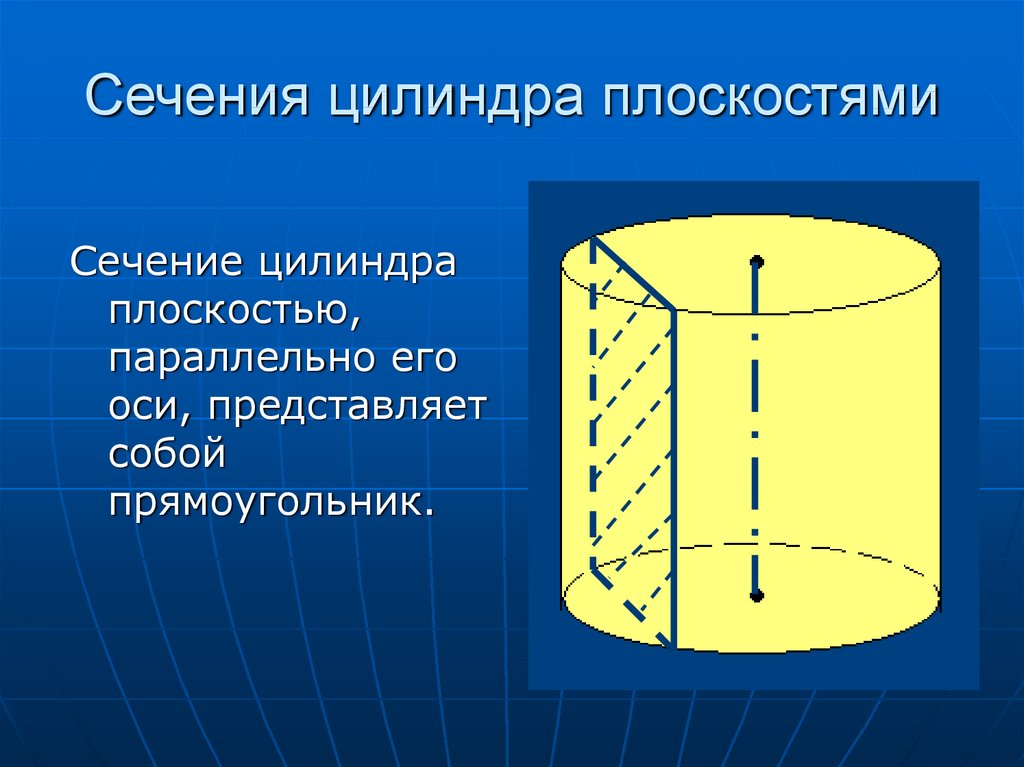
15. Сечения цилиндра плоскостями
Сечение цилиндраплоскостью,
параллельно его
оси, представляет
собой
прямоугольник.
16.
Если секущая плоскостьпроходит через ось
цилиндра, то сечение
представляет собой
прямоугольник, две
стороны которого –
образующие, а две
другие - диаметры
оснований цилиндра.
Такое сечение
называется осевым
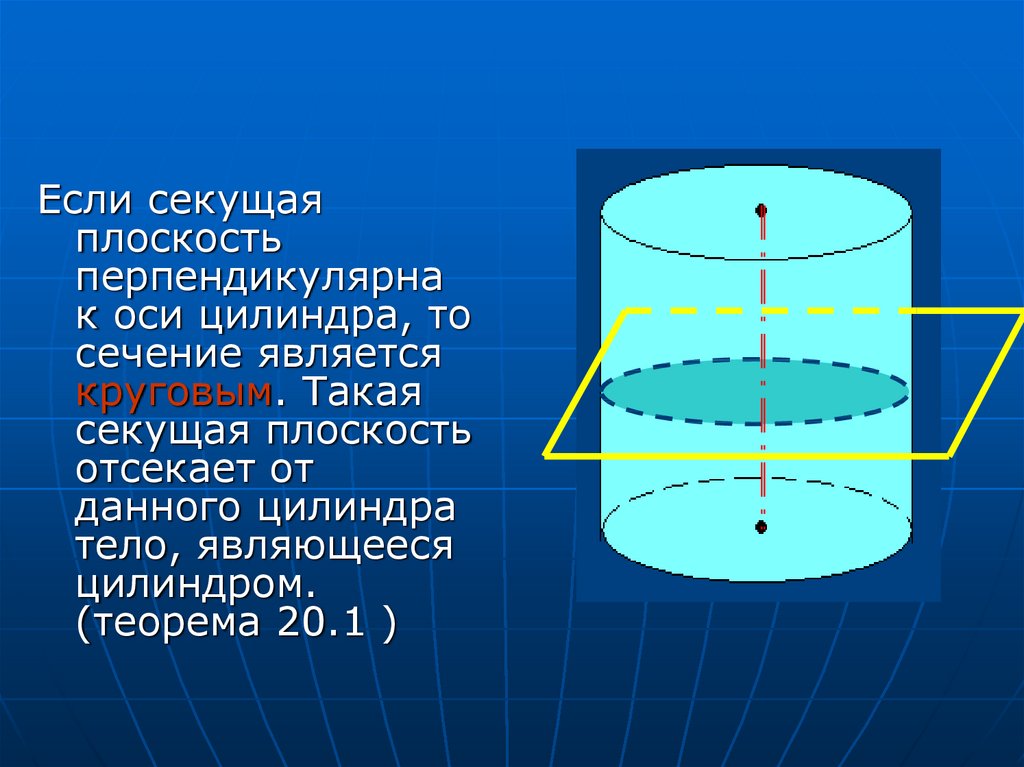
17.
Если секущаяплоскость
перпендикулярна
к оси цилиндра, то
сечение является
круговым. Такая
секущая плоскость
отсекает от
данного цилиндра
тело, являющееся
цилиндром.
(теорема 20.1 )
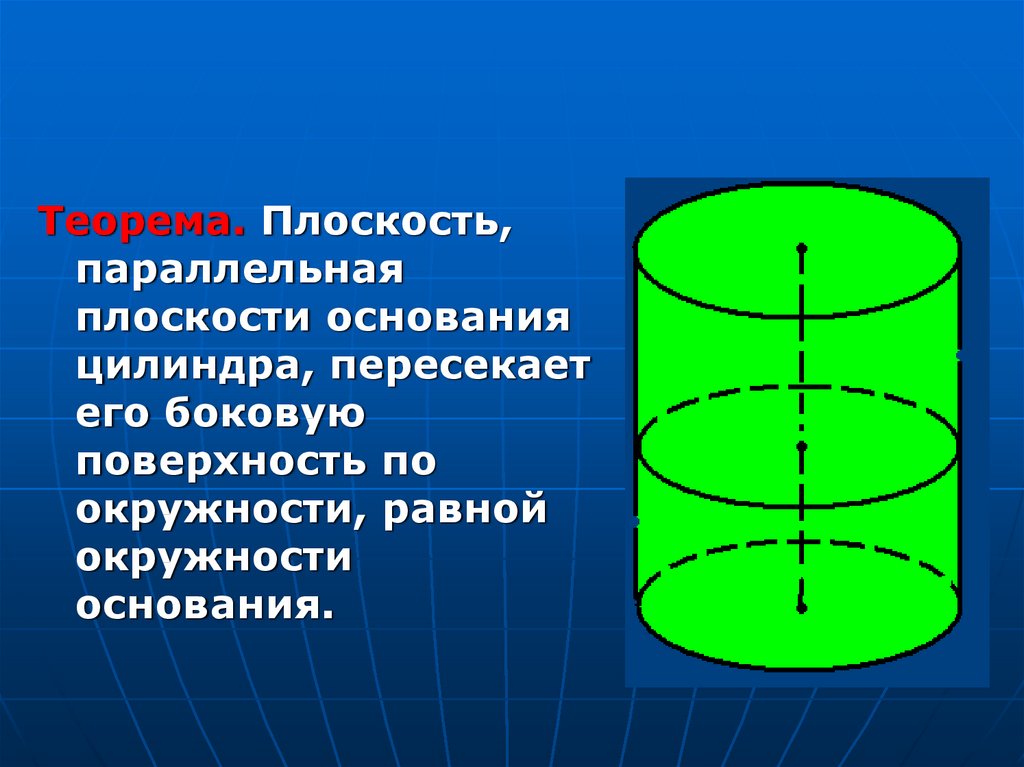
18.
Теорема. Плоскость,параллельная
плоскости основания
цилиндра, пересекает
его боковую
поверхность по
окружности, равной
окружности
основания.
19.
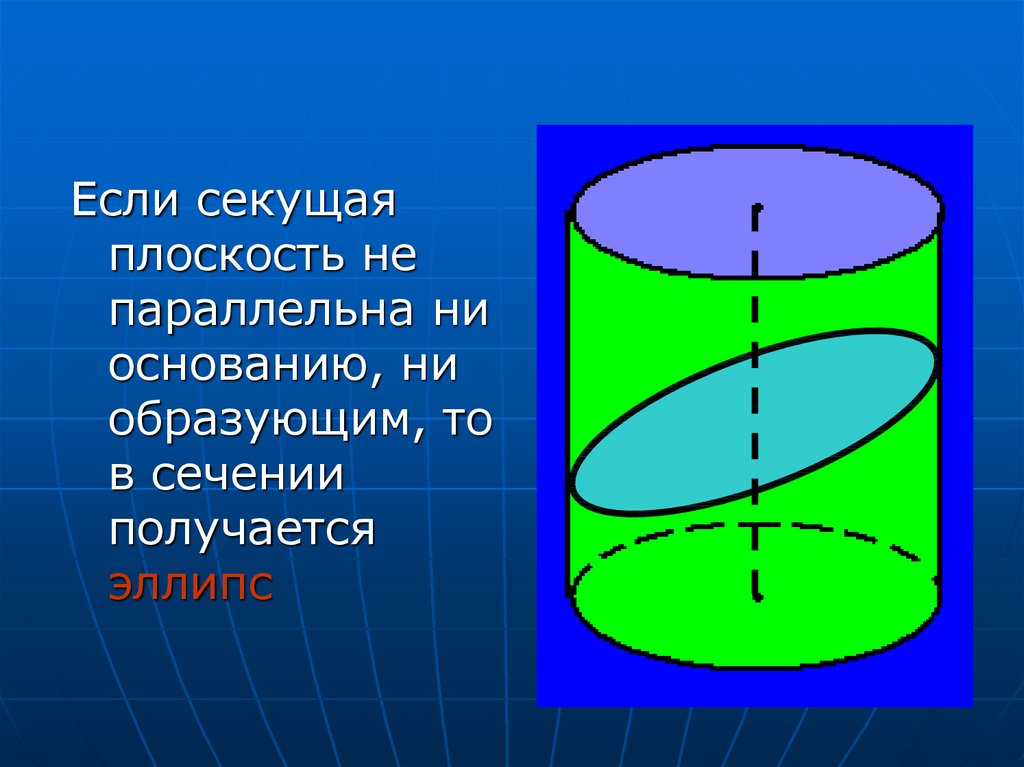
Если секущаяплоскость не
параллельна ни
основанию, ни
образующим, то
в сечении
получается
эллипс
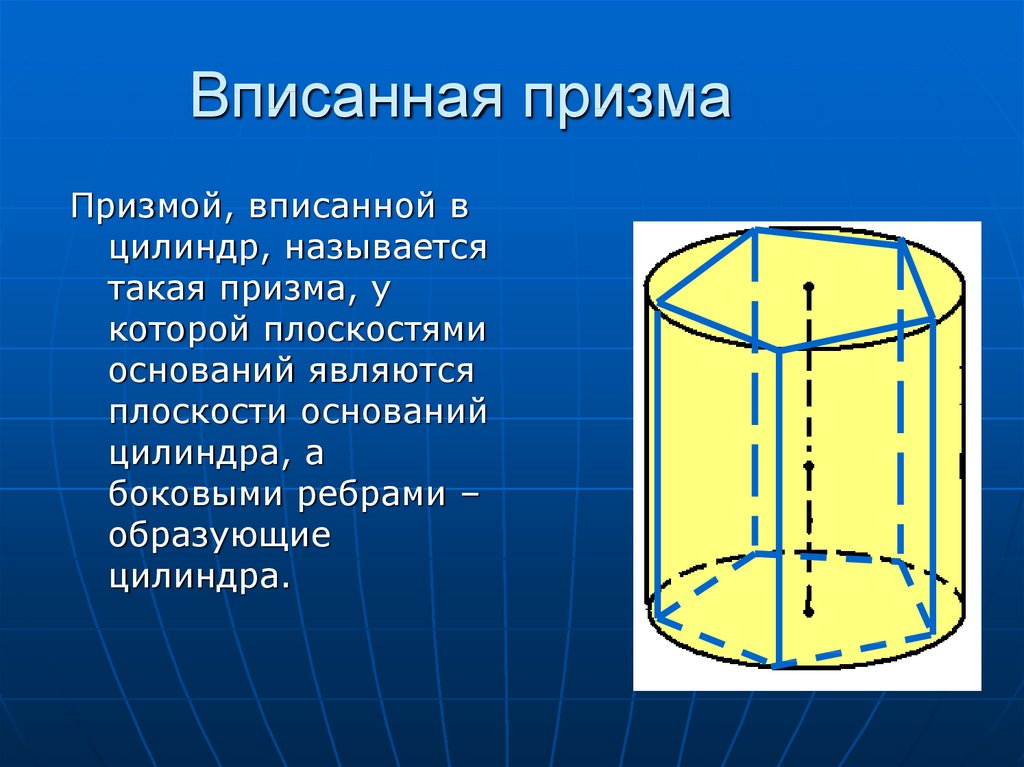
20. Вписанная призма
Призмой, вписанной вцилиндр, называется
такая призма, у
которой плоскостями
оснований являются
плоскости оснований
цилиндра, а
боковыми ребрами –
образующие
цилиндра.
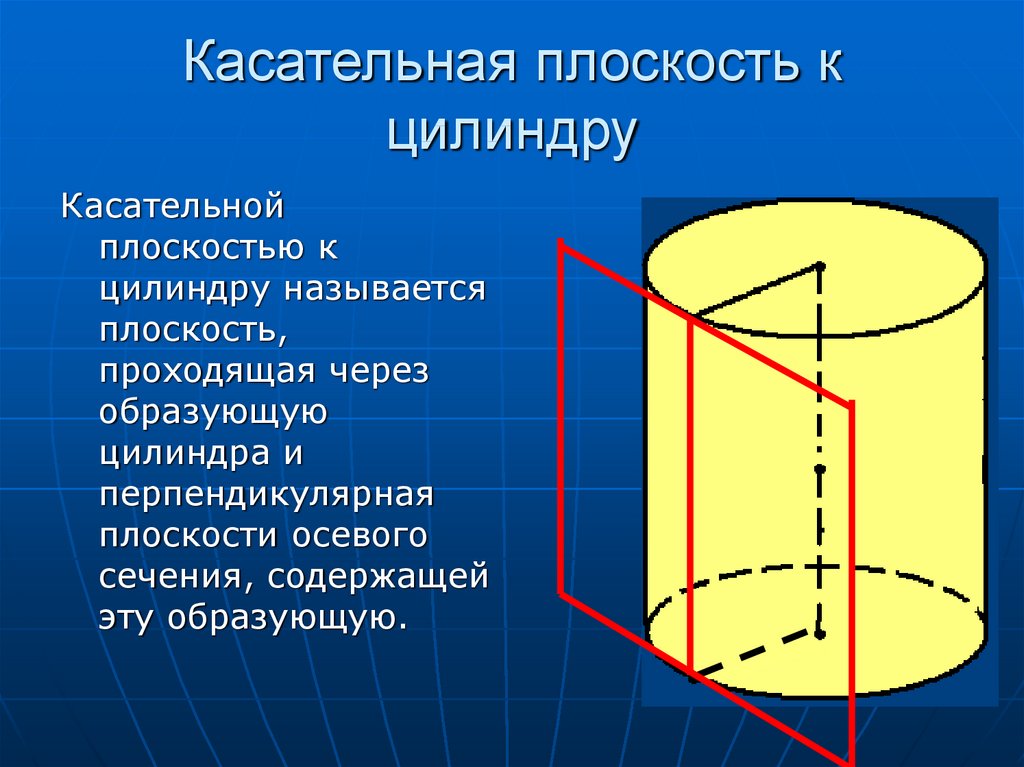
21. Касательная плоскость к цилиндру
Касательнойплоскостью к
цилиндру называется
плоскость,
проходящая через
образующую
цилиндра и
перпендикулярная
плоскости осевого
сечения, содержащей
эту образующую.
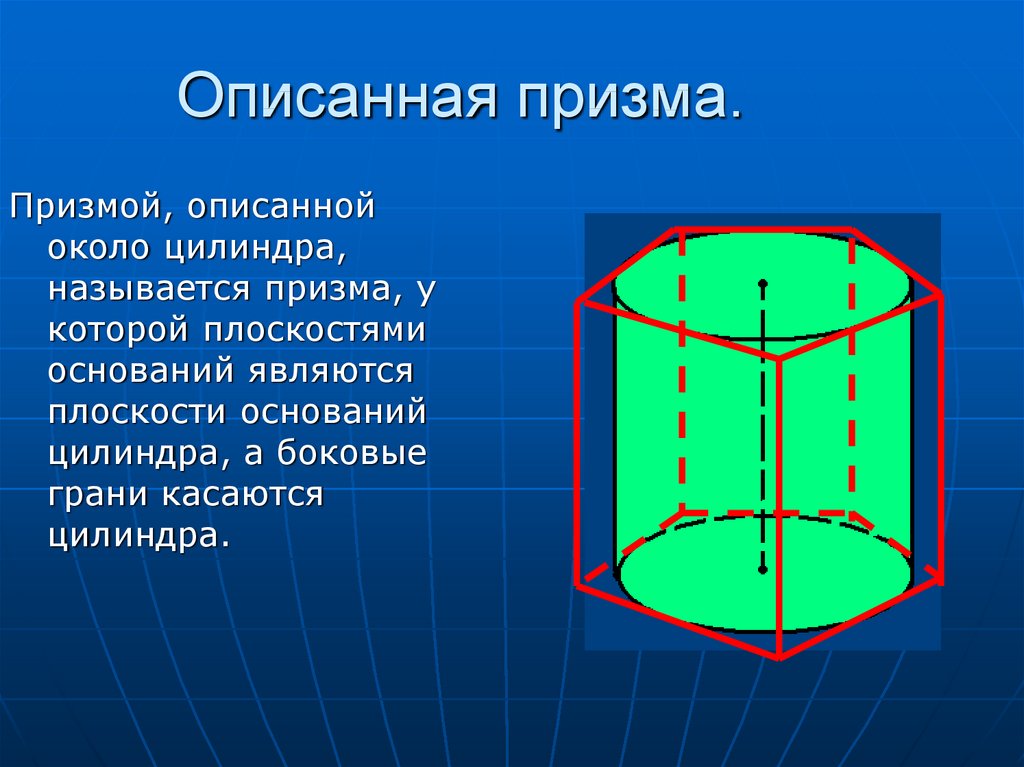
22. Описанная призма.
Призмой, описаннойоколо цилиндра,
называется призма, у
которой плоскостями
оснований являются
плоскости оснований
цилиндра, а боковые
грани касаются
цилиндра.
23. Площадь полной поверхности цилиндра
Площадь боковой поверхности+
Две площади основания
24.
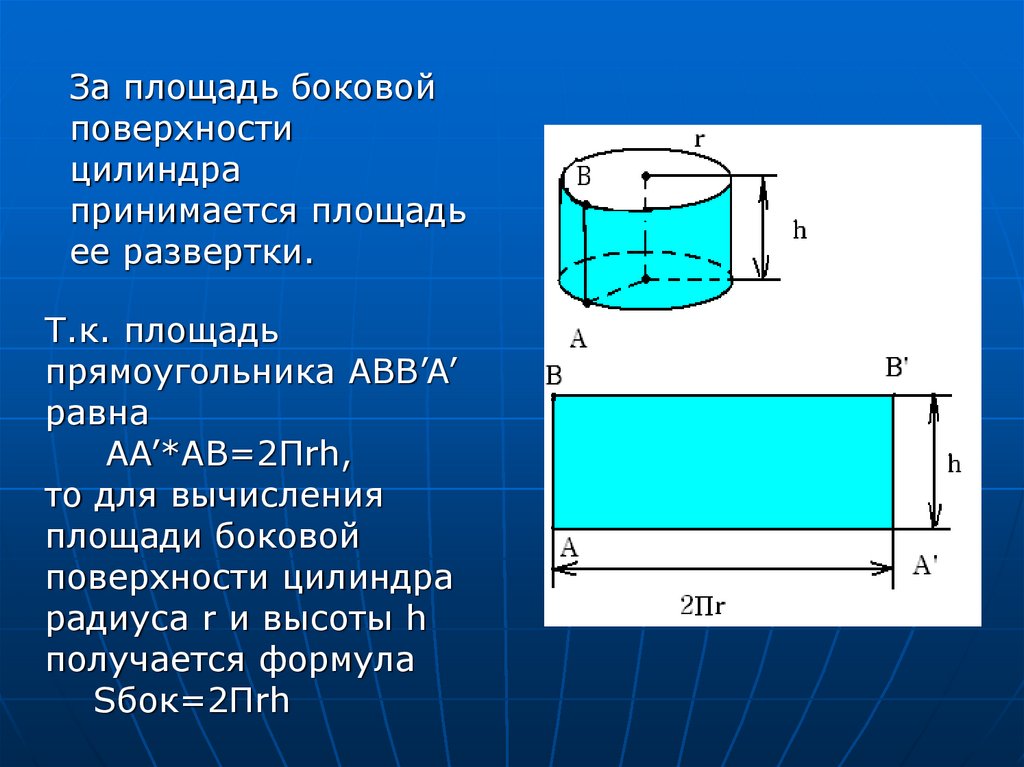
За площадь боковойповерхности
цилиндра
принимается площадь
ее развертки.
Т.к. площадь
прямоугольника ABB’A’
равна
AA’*AB=2Пrh,
то для вычисления
площади боковой
поверхности цилиндра
радиуса r и высоты h
получается формула
Sбок=2Пrh
25. Площадь основания
Площадь каждогооснования равна
26.
Площадь полнойповерхности цилиндра
вычисляется по формуле
27.
Объём цилиндравычисляется по формуле
28. Найти площадь полной поверхности цилиндра
В5
А
45º
r
С
АВС
-
прямоугольный
АВС
-
равнобедренный
ВС=АС=5
r=2,5
S=2πr(h+r)
S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5π
29.
Площадь осевого сечения цилиндра равна 10 м2, аплощадь основания равна 5 м2. Найдите высоту
цилиндра.
R 5,
2 R H 10
2
В
O1
С
H
А
R
O
R=
D
H=
2
5
5
H
5
H
5
м
30.
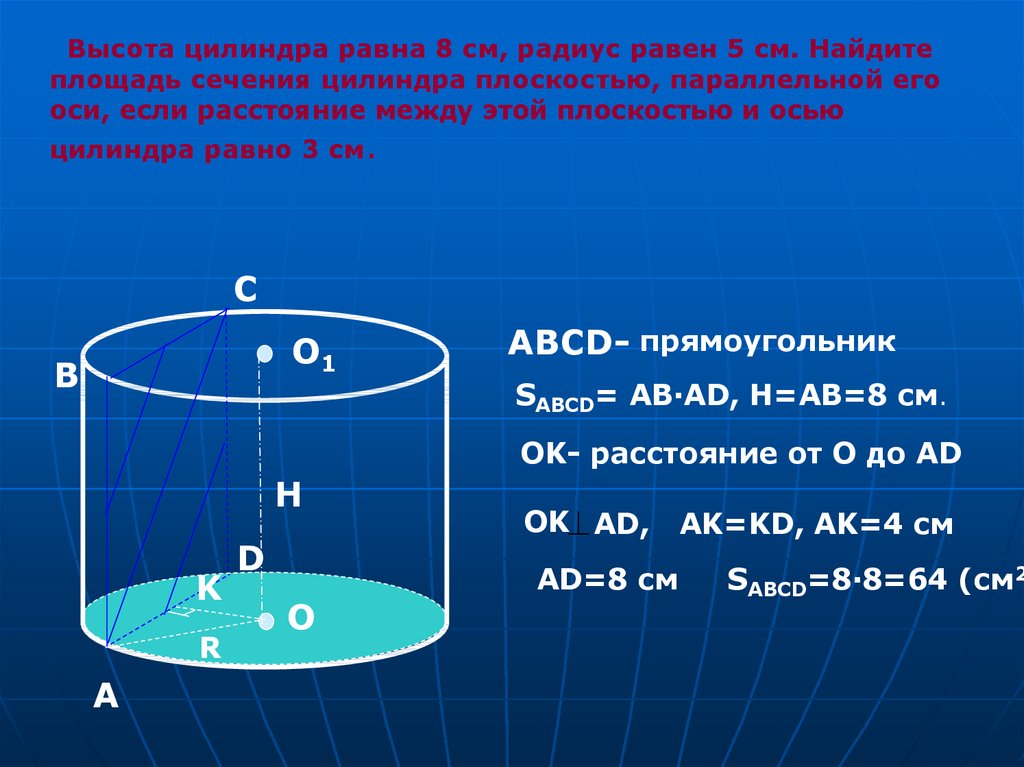
Высота цилиндра равна 8 см, радиус равен 5 см. Найдитеплощадь сечения цилиндра плоскостью, параллельной его
оси, если расстояние между этой плоскостью и осью
цилиндра равно 3 см.
C
O1
B
ABCD- прямоугольник
SABCD= AB·AD, H=AB=8 см.
OK- расстояние от О до AD
H
K
R
A
D
O
OK AD,
AD=8 см
AK=KD, AK=4 см
SABCD=8·8=64 (см2
31. Дано: цилиндр, Н= 8 см . R= 5 см, ОК= 3 см. Сечение АВСД параллельно оси цилиндра. Найти: площадь сечения АВСД.
.Дано: цилиндр, Н= 8 см . R= 5 см, ОК= 3 см.
Сечение АВСД параллельно оси цилиндра.
Найти: площадь сечения АВСД.
Ответ: 64 см².
32. Осевое сечение - квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) площадь основания цилиндра.
Ответ: 10 см, 50π см².33.
Спасибо завнимание!



















 Математика
Математика








