Introduction to Finance: Chapter 9. Time Value of Money

1. Introduction to Finance: Chapter 9. Time Value of Money

The Time Value of Money (TVM) states that money today
is worth more than the same amount in the future due to
its earning potential. Compounding grows money by
earning interest on both principal and past interest,
while discounting finds the present value of future cash
flows. Annuities involve periodic payments, with
formulas to determine their present and future values,
interest rates, and payment amounts. TVM also applies
to shorter time intervals, influencing consumer credit
costs and investment decisions. Understanding these
concepts is key to making informed financial choices in
savings, loans, and investments.
by Rustem Karimov, SDU University, BS, Kaskelen, 2025

2. Overview

Future Value
Present Value
Finding I and N
Annuities
Rates of Return
Amortization

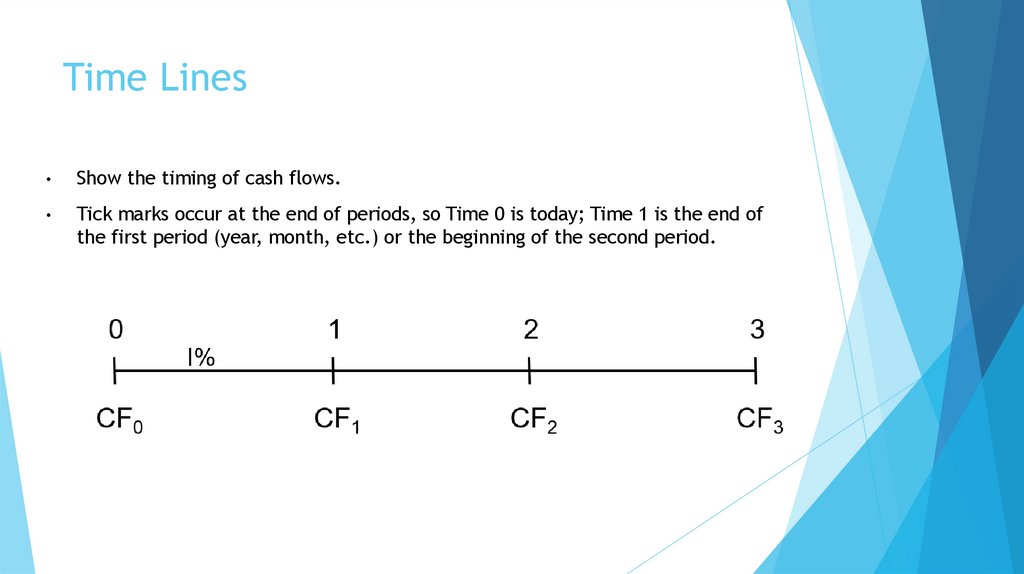
3. Time Lines

Show the timing of cash flows.
Tick marks occur at the end of periods, so Time 0 is today; Time 1 is the end of
the first period (year, month, etc.) or the beginning of the second period.

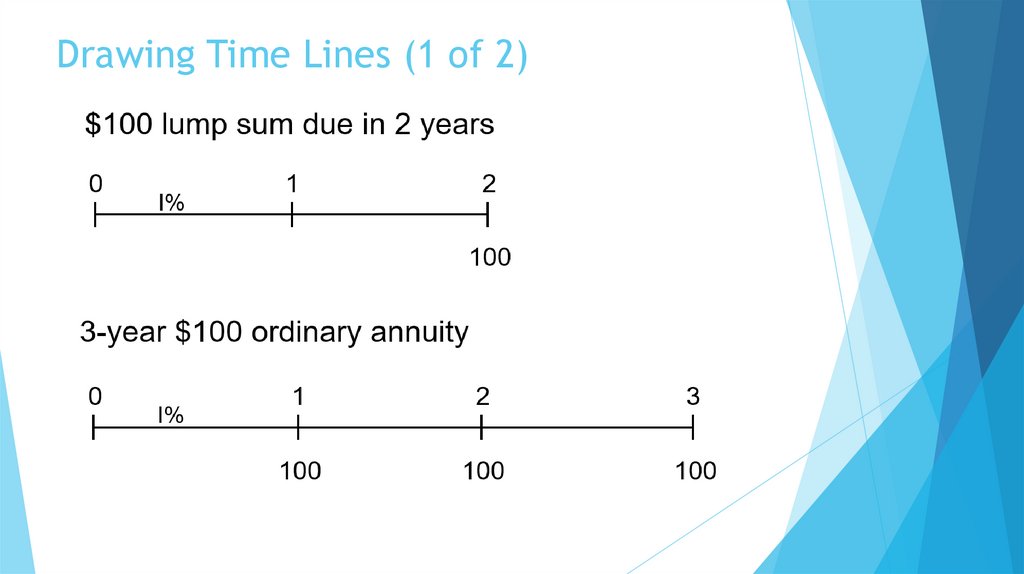
4. Drawing Time Lines (1 of 2)

5. Drawing Time Lines (2 of 2)

Uneven cash flow stream - refers to a series of cash flows that vary in
amount over time.
These types of cash flow streams are common in many real-world
financial situations, such as business investments, project evaluations, or
irregular loan payments.
Characteristics of Uneven Cash Flow Streams
1.Irregular Amounts: Each cash flow may differ in size.
2.Unpredictable Timing: Cash flows may not occur at regular intervals.
3.Positive or Negative: Cash flows can be both inflows (positive) or
outflows (negative).

6. Drawing Time Lines (2 of 2)

Practical Examples
1.Capital Investments: A company invests in a new project
that generates different revenue and cost amounts each year.
2.Start-Up Cash Flows: A start-up may have negative cash
flows at the beginning (expenses) and fluctuating positive
cash flows as it grows.
3.Irregular Loan Repayments: A borrower may make irregular
payments based on their financial situation.

7. The Future value (FV)

Future Value (FV) – is the amount to which a cash flow or series of
cash flows will grow over a given period of time when compounded
at a given interest rate.
Future Value (FV) is a way to understand how much money will be
worth in the future if you invest it today at a certain interest
rate.

8. The Future value (FV)

Example:
If you invest $1,000 (PV) at an interest rate of 5% (0.05) for 3 years
(n), the calculation would look like this:
So, the Future Value of your investment would be approximately
$1,157.63 after 3 years.

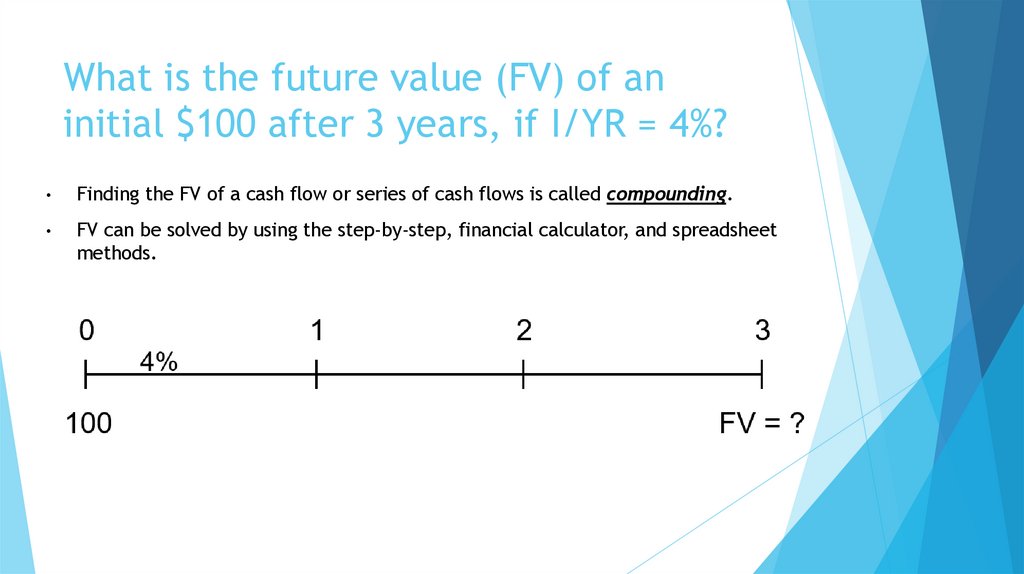
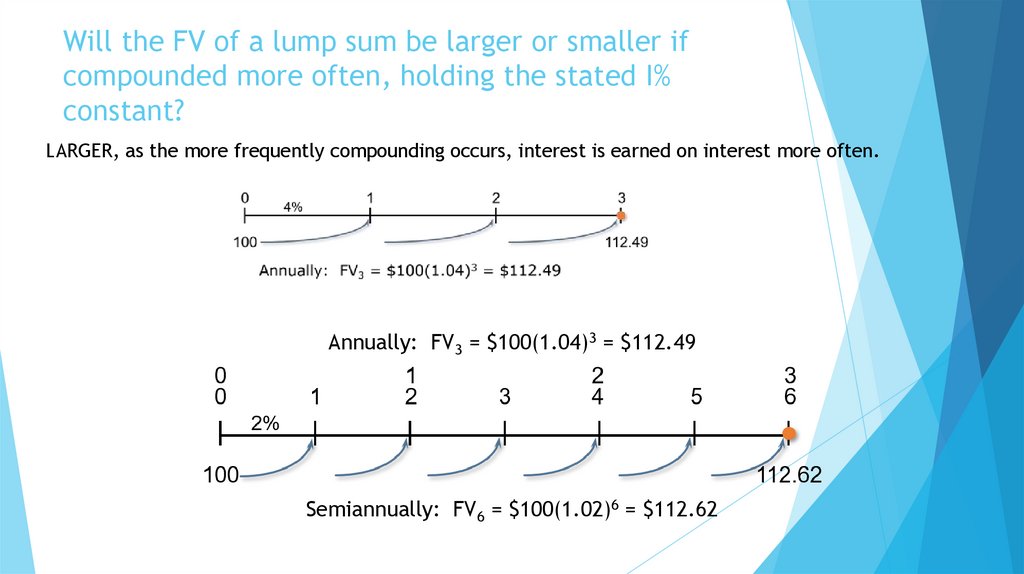
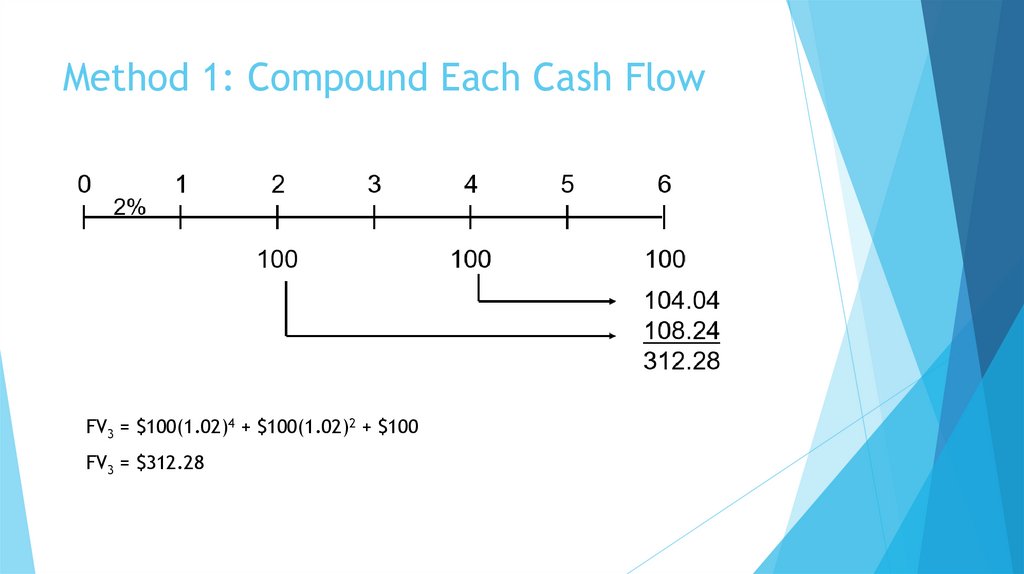
9. What is the future value (FV) of an initial $100 after 3 years, if I/YR = 4%?

Finding the FV of a cash flow or series of cash flows is called compounding.
FV can be solved by using the step-by-step, financial calculator, and spreadsheet
methods.

10. Solving for FV: The Step-by-Step and Formula Methods

After 1 year:
FV1 = PV(1 + I) = $100(1.04) = $104.00
After 2 years:
FV2 = PV(1 + I)2 = $100(1.04)2 = $108.16
After 3 years:
FV3 = PV(1 + I)3 = $100(1.04)3 = $112.49
After N years (general case):
FVN = PV(1 + I)N

11. Financial Calculator

A financial calculator is a specialized calculator designed to perform financial
calculations quickly and efficiently.
Key Functions
1. Time Value of Money (TVM) Calculations:
1. PV: Calculate the present value of a future cash flow.
2. FV: Calculate the future value of an investment based on periodic
payments and interest rates.
3. Interest Rate (I/Y): Calculate the interest rate for a given investment or
loan.
4. Number of Periods (N): Determine how long it will take to reach a
certain amount of money.
2. Loan Calculations:
1. PMT: Calculate the payment amount for a loan based on the principal,
interest rate, and number of payments.
3. Cash Flow Analysis:
1. NPV (Net Present Value): Calculate the present value of a series of
cash flows.
2. IRR (Internal Rate of Return): Find the interest rate that makes the net
present value of cash flows equal to zero.

12. Financial Calculator

Financial Calculator is beneficial for anyone involved in financial decision-making:
1. Finance Professionals
• Financial Analysts: Use financial calculators for time value of money (TVM) calculations,
bond valuation, net present value (NPV), internal rate of return (IRR), and investment
analysis.
• Accountants: Utilize them for cash flow analysis, depreciation calculations, and
budgeting.
• Investment Bankers: Use them for mergers and acquisitions (M&A) valuation, financial
modeling, and capital budgeting.
• Financial Advisors and Planners: Employ them to develop financial plans for clients,
including retirement planning, mortgage calculations, and investment strategies.
2. Students and Academics
• Finance and Economics Students: Use financial calculators to understand concepts
such as present value, future value, annuities, and amortization schedules.
• MBA Students: Find them essential for solving case studies involving financial modeling,
valuation, and risk assessment.
• CFA, CPA, and CFP Candidates: Require these calculators for exams and practical
applications of complex financial formulas and investment management scenarios.
Other users of financial calculator: Real Estate Professionals, Business Owners and Entrepreneurs,
Loan Officers and Mortgage Brokers, Individuals Making Personal Financial Decisions

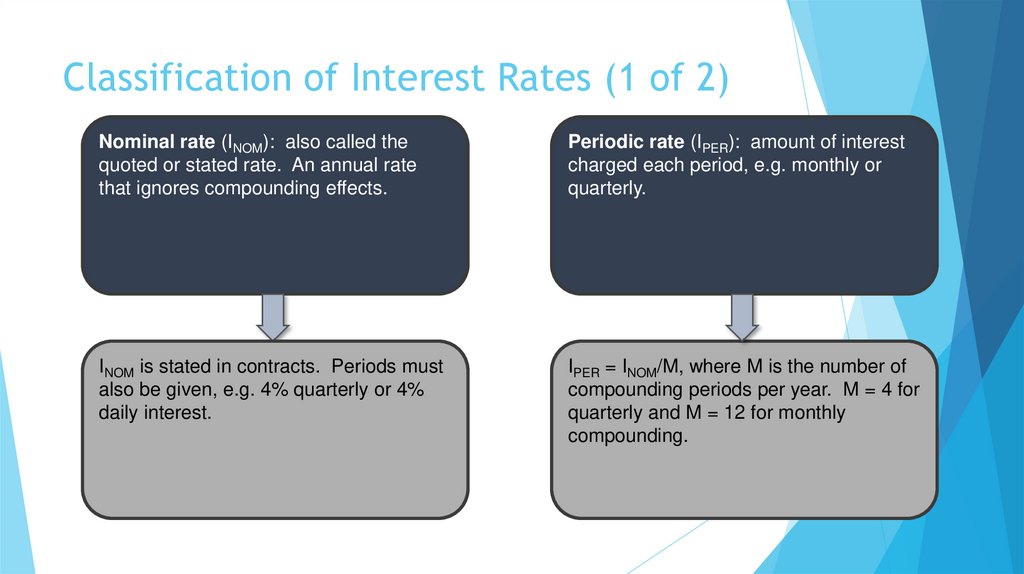
13. Solving for FV: Calculator and Excel Methods

Solves the general FV equation.
Requires 4 inputs into calculator, and will solve for the fifth. (Set to P/YR = 1 and
END mode.)
Excel: =FV(rate,nper,pmt,pv,type)

14. The Present Value (PV)

Present Value (PV) – is the value today of a future cash flow or series of
cash flows.
Present Value (PV) is the current worth of a sum of money that you expect
to receive in the future, discounted back to today’s value using a specific
interest rate. It helps you understand how much a future cash flow is worth
in today’s terms.

15. The Present Value (PV)

Example:
If you expect to receive $1,157.63 (FV) in 3 years at an interest rate of 5%
(0.05), the calculation for Present Value would be:
So, the Present Value of receiving $1,157.63 in 3 years at a 5% interest rate is
approximately $1,000 today. This means if you invest $1,000 today at a 5%
interest rate, it will grow to $1,157.63 in 3 years.

16. Present Value

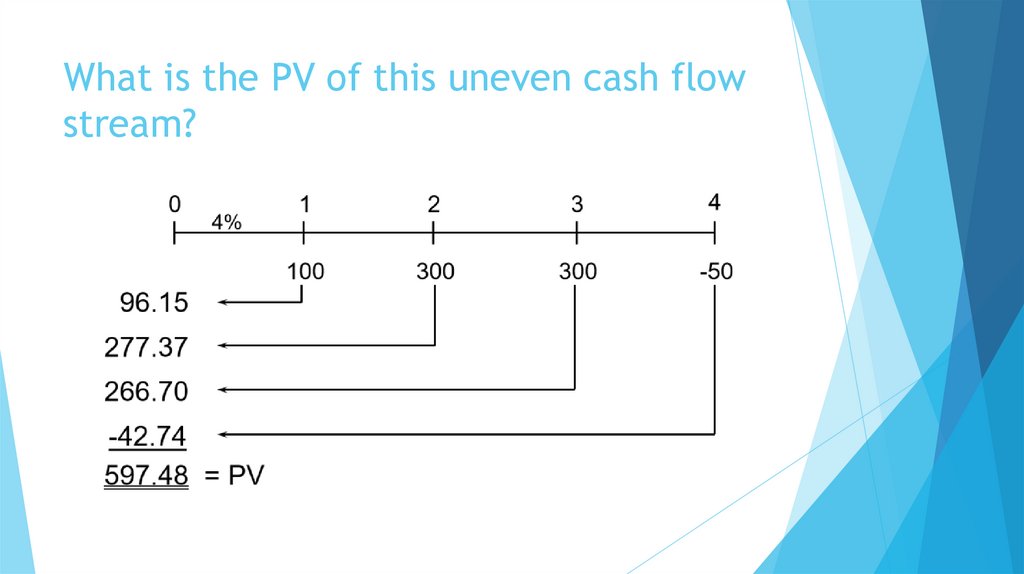
What is the present value (PV) of $100 due in 3 years, if I/YR = 4%?
Finding the PV of a cash flow or series of cash flows is called discounting (the reverse of
compounding).
The PV shows the value of cash flows in terms of today’s purchasing power.

17. Solving for PV: The Formula Method

Solve the general FV equation for PV:
PV = FVN /(1 + I)N
PV = FV3 /(1 + I)3
= $100/(1.04)3
= $88.90

18. Solving for PV: Calculator and Excel Methods

Solves the general FV equation for PV.
Exactly like solving for FV, except we have different input information and are solving for a different
variable.
Excel: =PV(rate,nper,pmt,fv,type)

19. Using the Financial Calculator

Steps to Calculate PV:
1. Clear Previous Entries:
• Turn on the calculator.
• Press [2nd] and then [CLR TVM] (above the FV button) to clear any previous time value of
money (TVM) entries. This ensures that no old data interferes with the new calculation.
2. Set the Number of Periods (N):
• Press 3, then press the [N] button.
• This sets the total number of periods to 3.
3. Set the Interest Rate (I/YR):
• Press 4, then press the [I/YR] button.
• This sets the annual interest rate to 4%.
4. Set the Payment (PMT):
• Press 0, then press the [PMT] button.
• This sets the payment amount to zero since there are no periodic payments involved in
this calculation.
5. Set the Future Value (FV):
• Press 100, then press the [FV] button.
• This sets the future value to 100, which is the amount you want in 3 periods.
6. Compute the Present Value (PV):
• Press [CPT] (Compute), and then press [PV].
• The calculator will display the present value.
The calculator should display -88.90 as the present value, which corresponds to a cash
outflow (negative sign) indicating the amount that must be invested today.

20. Solving for I

What annual interest rate would cause $100 to grow to $119.10 in 3 years?
Solves the general FV equation for I/YR.
Hard to solve without a financial calculator or spreadsheet.
Excel: =RATE(nper,pmt,pv,fv,type,guess)

21. Solving for I

To find the annual interest rate that would cause $100 to grow to $119.10 in 3
years, we can use the Future Value (FV) formula for compound interest:
The annual interest rate that would cause
$100 to grow to $119.10 in 3 years is
approximately 6.00%.

22. Solving for N

If sales grow at 10% per year, how long before sales double?
Solves the general FV equation for N.
Hard to solve without a financial calculator or spreadsheet.
Excel: =NPER(rate,pmt,pv,fv,type)

23. Solving for N

If sales grow at 10% per year, how long before sales double?
The calculation uses the future value (FV) equation:
Where:
FV is the future value (2 in this case, since sales are doubling).
PV is the present value (1 or -1, representing the current sales).
r is the growth rate per period (10% or 0.10 in this case).
N is the number of periods (years in this case), which is the unknown.
This calculation is based on the formula:

24. The Annuities

• An annuity is a financial product or a structured series of payments made at
equal intervals over time.
• The payments can be made or received either on a regular basis (such as
monthly, quarterly, or annually).
• Applications of Annuities
Annuities are used for various financial purposes, including:
Retirement Planning: Many individuals use annuities to save for or receive
income during retirement.
Loans and Mortgages: Annuities help calculate regular loan payments.
Investments: Annuities can be investment vehicles that offer periodic returns
based on capital contributions.

25. The Annuities: Ordinary Annuity

Definition: An ordinary annuity is a series of equal payments made at the end of
each period over a specified number of periods.
Example: If you have a retirement plan that pays you $1,000 at the end of each
year for 5 years, that is an ordinary annuity. You receive your payments at the end
of each year.

26. The Annuities: Annuity Due

Definition: An annuity due is a series of equal payments made at the beginning of
each period over a specified number of periods.
Example: If you rent an apartment and pay $1,000 at the start of each month for 12
months, that is an annuity due. You pay at the beginning of each month.
Formula to calculate the present value (PV) of an annuity due:
*The variables have the same meaning as in the ordinary annuity formula.

27. What is the difference between an ordinary annuity and an annuity due?

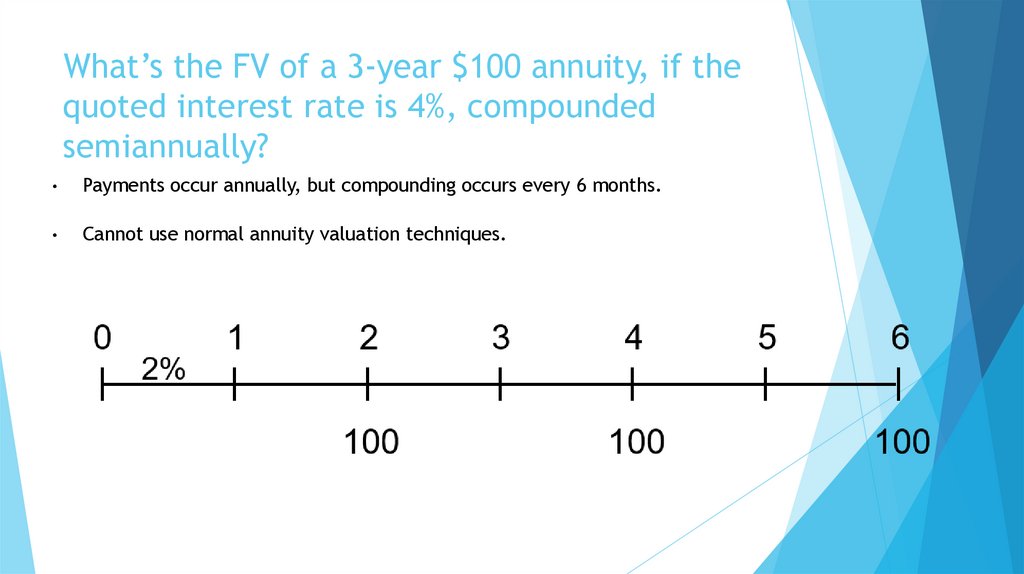
28. Solving for FV (1 of 3)

Given a 3-Year Ordinary Annuity of $100 at 4%
$100 payments occur at the end of each period, but there is no PV.
Excel: =FV(rate,nper,pmt,pv,type)
Here type = 0.

29. Solving for FV (1 of 3)

Given a 3-Year Ordinary Annuity of $100 at 4%.
The formula for the future value (FV) of an ordinary annuity is:
Where:
PMT is the payment per period (in this case, -100 since payments are outflows).
r is the interest rate per period (in this case, 4% or 0.04).
N is the number of periods (3 years).
Now, applying the formula:
So, the future value of the 3-year ordinary annuity with $100 payments at 4%
interest is $312.16.

30. Solving for PV

Given a 3-year Ordinary Annuity of $100 at 4%
100 payments still occur at the end of each period, but now there is no FV.
Excel: =PV(rate,nper,pmt,fv,type)
Here type = 0.

31. Solving for FV: 3-Year Annuity Due of $100 at 4%

Now, $100 payments occur at the beginning of each period.
FVAdue= FVAord(1 + I) = $312.16(1.04) = $324.65
Alternatively, set calculator to “BEGIN” mode and solve for the FV of the annuity due:
Excel: = FV(rate,nper,pmt,pv,type)
Here type = 1.

32. Solving for PV: 3-Year Annuity Due of $100 at 4%

Again, $100 payments occur at the beginning of each period.
PVAdue = PVAord(1 + I) = $277.51(1.04) = $288.61
Alternatively, set calculator to “BEGIN” mode and solve for the PV of the annuity due:
Excel: = PV(rate,nper,pmt,fv,type)
Here type = 1.

33. PV Calculation

What is the present value of a 5-year $100 ordinary annuity at 4%?
Be sure your financial calculator is set back to END mode and solve
for PV:
N = 5, I/YR = 4, PMT = -100, FV = 0.
PV = $445.18.

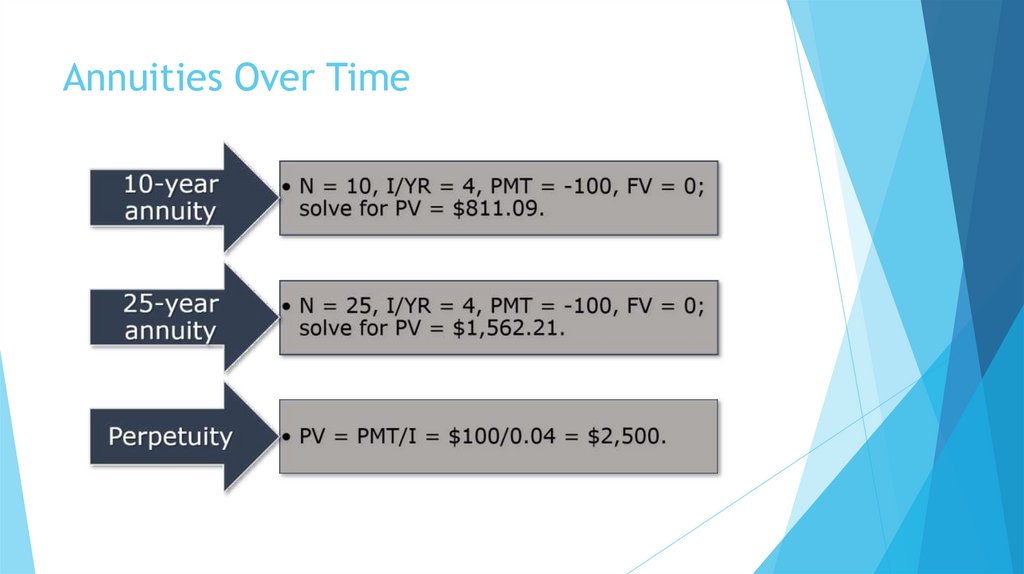
34. Annuities Over Time

35. Annuities Over Time

36. Annuities Over Time

37. The Power of Compound Interest

A 20-year-old student wants to save $5 a day for her
retirement. Every day she places $5 in a drawer. At the
end of the year, she invests the accumulated savings
($1,825) in a brokerage account with an expected annual
return of 8%.

38. Solving for FV (2 of 3)

If she begins saving today, how much will she have when she is 65?
If she sticks to her plan, she will have $705,373 when she is 65.
Excel: = FV(.08,45,-1825,0,0)

39. The Power of Compound Interest

Since she invests the amount annually at the end of the
year, we can use the Future Value of an Ordinary Annuity
formula:
Where:
FV = Future value of the investment
P = Annual savings = $1,825