Химия. Тема 1. Строение атома

1.

Химия – теоретический курс ОСНОВЫ ОБЩЕЙ ХИМИИ
В лекциях и Учебн.пособ.1 (УП 1) Основы общей химии
Анатолий Анатольевич БАРУНИН - лектор
ЛИТЕРАТУРА (основная – 1-2; дополнительная - 3-6):
Основная (1-2) – 1. Основы общей химии А.П.КИСЕЛЕВ и др.
-Учебн.пос.2012 г (УП 1). № в библиотеке БГТУ- (1262) есть в
текст. (книга) и электронном виде, а также в Курсе химии в папке
ЛИТЕРАТУРА → ОСНОВНАЯ ЛИТ-РА_Уч. пособ. кафедры: - книга под № 1
2. Другие учебные пособия и метод.указания кафедры – есть в
книжном и электронном виде в библиотеке БГТУ и в Курсе химии в
папке ЛИТЕРАТУРА → ОСНОВНАЯ ЛИТ-РА_Уч. пособ. каф.: - книги № 2-11
Дополнительная (3-6) – учебники химии различных авторов:
3. А.И. Горбунов, А.А. Гуров и др. Теоретические основы общей
химии; 4. А.В. Суворов, А.Б. Никольский; 5. В.В. Фролов; 6. Н.В.
Коровин, а также книги других авторов – см.в библиотеке БГТУ

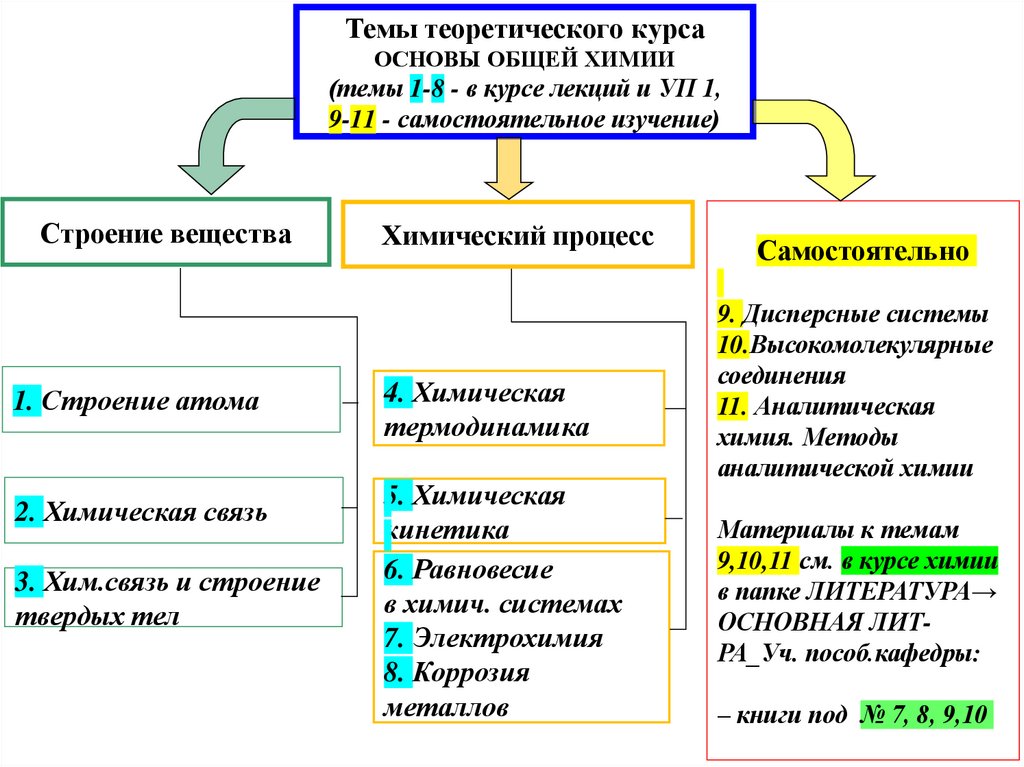
2. Темы теоретического курса ОСНОВЫ ОБЩЕЙ ХИМИИ (темы 1-8 - в курсе лекций и УП 1, 9-11 - самостоятельное изучение)

Строение вещества
1. Строение атома
2. Химическая связь
3. Хим.связь и строение
твердых тел
Химический процесс
4. Химическая
термодинамика
5. Химическая
кинетика
6. Равновесие
в химич. системах
7. Электрохимия
8. Коррозия
металлов
Самостоятельно
9. Дисперсные системы
10.Высокомолекулярные
соединения
11. Аналитическая
химия. Методы
аналитической химии
Материалы к темам
9,10,11 см. в курсе химии
в папке ЛИТЕРАТУРА→
ОСНОВНАЯ ЛИТРА_Уч. пособ.кафедры:
– книги под № 7, 8, 9,10

3.

Экзаменационные вопросы
1. Строение атома
1. Развитие представлений о строении атома. Физические модели. Корпускулярно-волновой дуализм
электромагнитного излучения. Формула Планка и Эйнштейна.
2. Гипотеза и уравнение де Бройля. Корпускулярно-волновые свойства материи. Опыты по дифракции
электрона.
3. Принцип неопределенности Гейзенберга. Понятия волновой механики. Уравнение стоячей волны. Уравнение
Шредингера. Физический смысл волновой функции.
4. Электрон в потенциальном ящике. Дискретность энергетических состояний электрона.
5. Квантово-механическое описание атома водорода в основном состоянии. Радиальное распределение
электронной плотности в атоме водорода. Понятие электронной орбитали.
6. Возбужденные состояния атома водорода. Квантовые числа. Их физический смысл. Пространственные
конфигурации электронных орбиталей. Энергетическая диаграмма орбиталей в атоме водорода. Понятие
энергетического вырождения.
7. Радиальное распределение электронной плотности для различных энергетических состояний атома
водорода. Многоэлектронный атом. Зависимость энергии орбиталей от заряда ядра атома и от различия
радиального распределения электронной плотности s, p и d-орбиталей (проникающей способности).
8. Электронные конфигурации многоэлектронных атомов. Правила заселения электронами атомных орбиталей
(АО). Связь электронной конфигурации атома с его положением в периодической таблице элементов.
9. Периодический закон Д.И. Менделеева и его связь с электронным строением атомов.
10. Физико-химические характеристики атомов – радиус атома и иона, энергия ионизации, энергия сродства к
электрону, электроотрицательнось (по Малликену и Полингу).

4. I. Строение атома УП 1 с.23-64 1.1 Развитие представлений о строении атома

3 этапа развития учения о строении атома
1 – Натурфилософские представления об атомном строении материи.
(5 в.до н.э.) Демокрит – понятие «атом». Эпикур, Аристотель.
2 – Химическая гипотеза об атоме (16-17 в.), как наименьшей частице хим.
элемента. Атомы отличаются массой. Парацельс, Бойль, Берцелиус.
До конца 19 в. атом рассматривался как неделимая частица.
3 – Физические модели строения атома (появились на рубеже 19-20 в.)
Описывают сложное строение атома. Появились на основании открытий, исслед.:
Исследование электролиза(1832) Майкл Фарадей
Открытие каналовых (1886) и катодных лучей (1896) Уильям Крукс
Открытие и измерение свойств электрона (1897) Джозеф Джон Томсон
Открытие естественной радиоактивности (1896) Анри Беккерель
Основной вывод из исследований и открытий 3-го этапа - атомы содержат
разноименно заряженные частицы (имеют сложное строение)

5. Физические модели строения атома

Эрнест Резерфорд - планетарная модель атома (1911 г.)
Атом - сложная частица, состоящая из положительно заряженного ядра (~10-15
м, почти вся масса атома в ядре малого размера) и отрицательно заряженных
электронов вращающихся вокруг ядра на расстоянии ~10-10 м (по характеру
рассеяния α-частиц тонкими Pt, Ag и Cu металлическими фольгами)
Нильс Бор – теория (модель) строения атома водорода (постулаты) (1913г.)
En = - 2π2e4k2m / h2 ∙ 1/n2 (n=1 E1= -13,6 эВ; En = - E1 / n2
rn = h2 / 4π2e2km ∙ n2 n = 1,2,3… Позволила рассчитать Е эл-на (объясняла
оптический линейчатый спектр атома водорода) и радиус rn электронных орбит.
Не объясняла тонкую структуру оптических спектров, образование хим.связи
Луи де Бройль, Вернер Гейзенберг, Макс Борн, Эрвин Шредингер и др. квантово-механическая модель (1925-27 г.г. по настоящее время). Создана на
положениях квантовой (волновая) механики - теории, устанавливающей
способ описания и законы движения микрочастиц. Базируется на 2-х
основных гипотезах-постулатах Л. де Бройля (корпускулярно-волновой дуализм
свойств материи) и В. Гейзенберга (принцип неопределенности для
микрочастиц)

6. Корпускулярно-волновой дуализм свойств материи [проблема природы лучистой энергии - эл.магн.излучения(ЭМИ)]

Частица (корпускула): m – масса, v -скорость
p = mv - импульс
E= mv2/2 - кинетическая энергия
Волна: l - длина волны
n- частота
Т - период
Электромагнитное излучение
Макс Планк E = h n h n – энергия кванта ЭМИ нагретого
1900 г.
тела (дискретная порция, квант, частица)
h = 6,6262 10-34 Дж с - постоянная Планка
n- частота излучения [с–1]
квант энергии любого ЭМИ– частица –
фотон (объяснение фотоэффекта)
Альберт Эйнштейн
1905 г.
m - масса фотона, кг; c = 2,99 79 108 м/сек - скорость света
E = m c2
mc2 = hn n с
Корпускулярно- l
h
m
cl
h
l
m c
волновой дуализм ЭМИ - связь характеристики фотона
(масса, импульс частицы) и характеристики волны
(частота, длина волны). ЭМИ: фотон - частица и/или волна
h
l
p
p = m c –
импульс фотона

7. 1.2 Луи де Бройль (1925)

(дуализм-общее свойство материи,
а не только ЭМИ) - гипотезапостулат о связи импульса P любого
движущегося матер.объекта
с длиной волны λ, представляющей
волновой характер его движения
Если электрон
обладает волновыми
свойствами должна
наблюд.дифракция:
Материальный объект
(частица): m - масса, v –
скорость, λ –длина волны
(наз. волна де Бройля)
h h
l
m v
p
m v2
Кинетическая энергия - E k
2
h
Длина волны - l
m = 9,11 10-31 кг
2 m Ek
Для эл-на при Ek=100 эВ(1эВ=1,602 10-19Дж), l = 1.2 Å (1 Å =10-10 м)
Дифракционная
l= 1.2 Å (Ni фольга)
решетки для электрона α- постоянная решетки
- кристалл.плоскости
ширина щели +
Ме монокристаллов
промежуток между
щелями

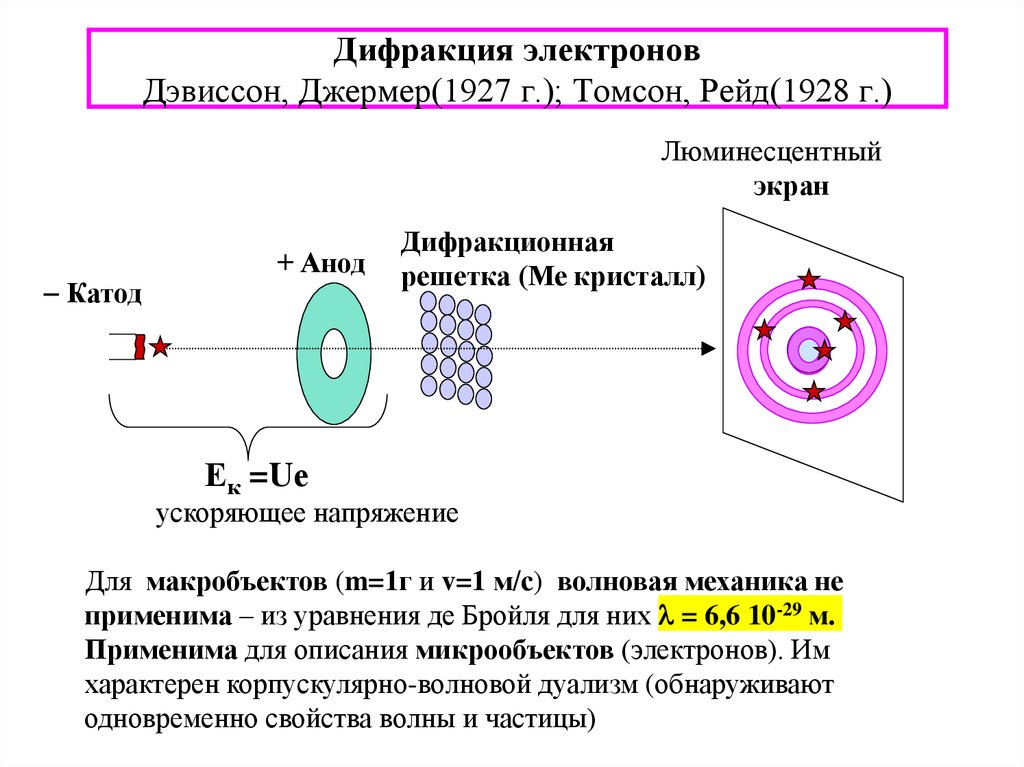
8. Дифракция электронов Дэвиссон, Джермер(1927 г.); Томсон, Рейд(1928 г.)

Люминесцентный
экран
Катод
+ Анод
Дифракционная
решетка (Ме кристалл)
Ек =Uе
ускоряющее напряжение
Для макробъектов (m=1г и v=1 м/с) волновая механика не
применима – из уравнения де Бройля для них l = 6,6 10-29 м.
Применима для описания микрообъектов (электронов). Им
характерен корпускулярно-волновой дуализм (обнаруживают
одновременно свойства волны и частицы)

9. Принцип неопределенности [для микрочастиц(электрона)]

Вернер Гейзенберг постулировал этот принцип в 1927 г.
(для одномерного пространства в виде неравенства):
∆х, ∆р х – неопределенность координаты частицы и
соответствующего ей импульса по оси х (аналогично по
оси y и z в 3-х мерном пространстве)
h
x p x
2
Одновременное точное определение координат частицы и ее импульса
невозможно. Заменяется определением вероятности нахождения частицы
в какой-то области пространства
Эрвином Шредингером и др. – на базе 2-х основных гипотез-постулатов Л.Де
Бройля и В.Гейзенберга [корпускул.-волновой дуализм микрочастиц и
неопределенность в точном измерении корпускулярных свойств микрочастиц
(координат и импульса)] разработана квантовая (волновая) механика,
устанавливающая способ описания и законы движения микрочастиц на
основе которой предложена квантово-механическая модель строения атома

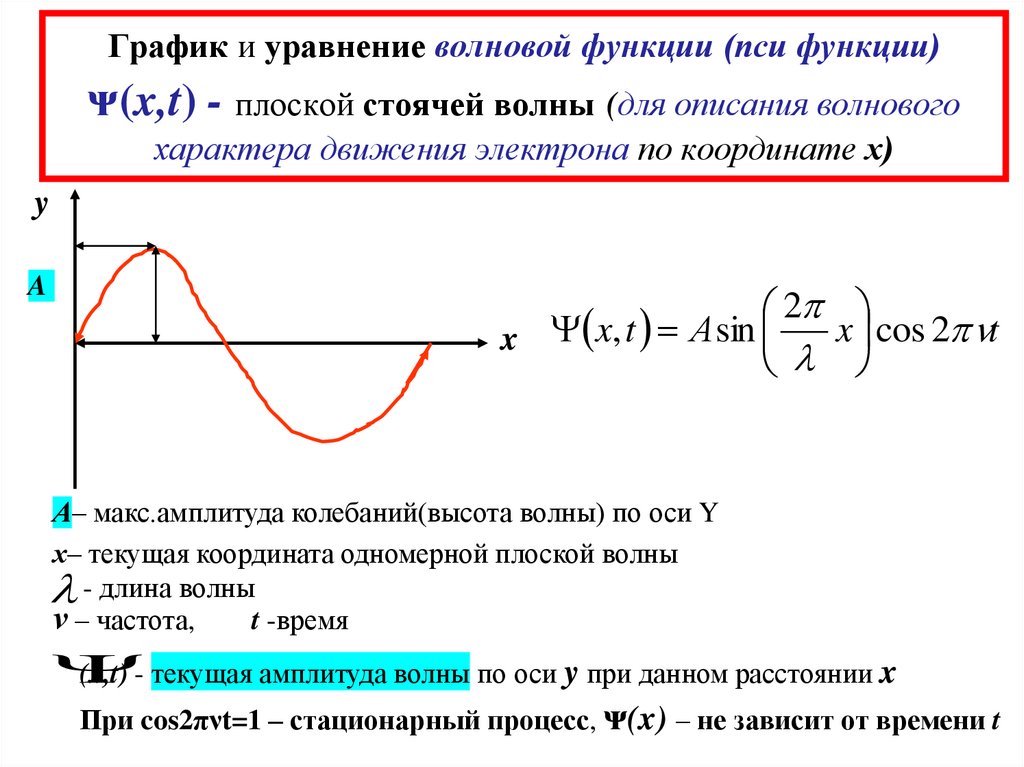
10. График и уравнение волновой функции (пси функции) ᴪ(x,t) - плоской стоячей волны (для описания волнового характера движения

электрона по координате х)
y
A
2
x cos 2 nt
x x, t А sin
l
А– макс.амплитуда колебаний(высота волны) по оси Y
х– текущая координата одномерной плоской волны
l - длина волны
ν – частота,
t -время
(x,t) - текущая амплитуда волны по оси y при данном расстоянии x
При cos2πνt=1 – стационарный процесс, ᴪ(x) – не зависит от времени t

11. Уравнение Шредингера

1. Для отображения волнового характера движения электрона в 3-х мерном
пространстве использ. уравнение с координатами (x,y,z) - (x,y,z,t)
(x,y,z,t) - волновая функция - пси функция (стоячая волна) - текущая амплитуда, функция координат (x,y,z) и времени (t);
(x,y,z) – (стоячая волна) для стационарн. процесса не зависит от времени t
– текущая амплитуда, функция координат (x,y,z);
(cos2πνt=1)
Дифф.уравнение 2-го порядка стоячей волны для стационарного процесса
в 3-х мерном пространстве с координатами (x,y,z) (*):
2 (x, y, z) 2 (x, y, z) 2 (x, y, z) 4 2
2 (x, y, z) 0
2
2
2
x
y
z
l
2
2
2
2
x
y
z
2
2
2
где l - длина волны
2 - оператор Лапласа (набла два) –
двойное дифференцирование функции
(здесь ) по координатам x, y и z (для
удобства записи уравнений используют)

12. 2. Уравнение должно содержать в себе характеристики электрона как волны - , так и частицы - m (дуализм микромира)

2. Уравнение должно содержать в себе характеристики электрона как
волны - l, так и частицы - m (дуализм микромира)
l m, Ek = mv 2 / 2 = m 2 v 2 / 2m
Длина волны де Бройля
l
mv = √2mE k
h
h
h
p m v
2 m Ek
2
h
λ2
2 m Ek
l 2 в (*) → Волнов.уравнен.движения свободного электрона (потенц.эн U=0):
8 2 m
(x, y, z)
E k (x, y, z) 0
2
h
2
Т.к. E = Ek + U, где E - полная энергия U- потенциальная Е k – кинетич.энергия
Подставляем Е k , получаем Волновое уравнение микрочастицы в
потенциальном поле [U ≠ 0], в частности, для
описания состояния электрона в квантовомеханической модели атома [в атоме U ≠ 0]
Уравнение Эрвина
Шрeдингера (1926 ): →
2
8
m
2
(x, y, z) 2 (E U) (x, y, z) 0
h

13. Физический смысл волновой функции

Макс Борн, 1926 г.
(x,y,z) - пси функция - волновая функция
• (x,y,z) - волновая (амплитудная) функция и физического смысла не имеет
• 2(x,y,z) - квадрат волновой функции пропорционален вероятности
(dP) нахождения частицы в элементарном объеме (dV) dV = dxdydz
dP = 2(x,y,z) dV
(**)
Из (**) → вероятность Pv
PV 2 (x, y, z)dV
нахождения частицы в объеме V:
V
Из (**) → плотность вероятности (или электронная
плотность для электрона) - вероятность нахождения
dP микрочастицы в элементарном объеме dV:
dP
2 (x, y, z)
dV
Принцип нормирования волновых функций Ψ(x,y,z)
PV = ∫v A2 |Ψ(x,y,z) |2 dV = 1,
А –нормирующий множитель

14. Электрон в одномерном потенциальном ящике(яме). Решение ур. Шредингера. Нахождение энергии электрона

Потенциальная яма (ящик) - область пространства, вне которой
потенциальная энергия U электрона обращается в бесконечность, т.е
электрон не может выйти за границы ящика (связанное состояние)модель для электрона в атоме
U
a
0
•Одномерный потенциальный ящик
Граничные условия (*) :
внутри ящика: 0<х<а потенц.энергия U= 0 →
на границах ящика: в (‧) 0 и (‧) а
U= →
x
(x)
(0)=0, (а)=0
Уравнение Шредингера для электрона в потенц.ящике:
d 2 (x) 8 2m
E (x) 0
dx 2
h2
Решение ур. Шредингера – нахождение так наз. собственных волновых
функций (x) ( должны быть конечны, однозначны, непрерывны) и расчет
соответствующих этим функциям (x) собственных значений энергий Е

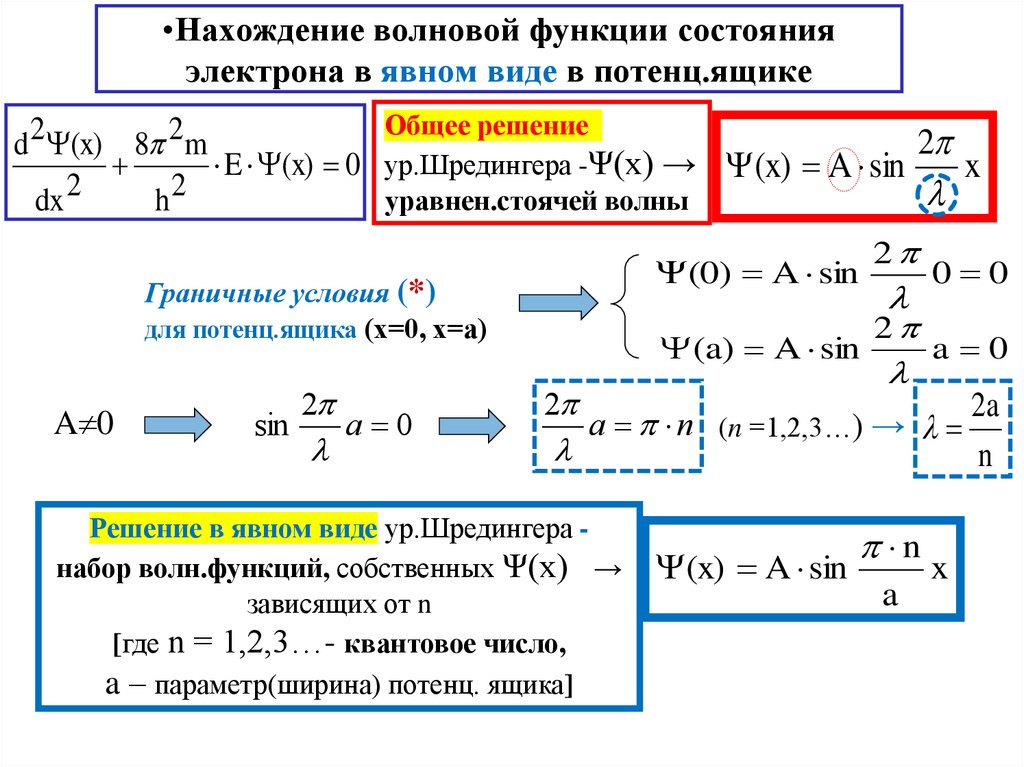
15. Нахождение волновой функции состояния электрона в явном виде в потенц.ящике

•Нахождение волновой функции состояния
электрона в явном виде в потенц.ящике
Общее решение
2
2
2
d (x) 8 m
E (x) 0 ур.Шредингера -Ψ(х) → (x) A sin
x
2
2
l
уравнен.стоячей волны
dx
h
Граничные условия (*)
для потенц.ящика (х=0, х=а)
A 0
sin
2
l
a 0
(0) A sin
2
0 0
l
2
(a) A sin
a 0
l
2
2a
a n (n =1,2,3…) → l
l
n
Решение в явном виде ур.Шредингера набор волн.функций, собственных Ψ(х) →
зависящих от n
[где n = 1,2,3…- квантовое число,
a – параметр(ширина) потенц. ящика]
(x) A sin
n
a
x

16. Нахождение энергии электрона в потенц.ящике [подстановка ᴪ(x) в ур.Шредингера]

•Нахождение энергии электрона в потенц.ящике
[подстановка
(x) A sin
n
a
x 0
d 2 (x)
2 n2
n
A
( sin
x)
2
2
dx
a
a
2 n2
n
2 n2
8 2 m
E 0
2
h
ᴪ(x) в ур.Шредингера]
d (x)
n
n
A
cos
x
dx
a
a
d 2 (x) 8 2m
E (x) 0
2
2
dx
h
8 2 m
n
A
( sin
x)
E A sin
x 0
2
2
a
a
h
a
n
2 n 2 8 2 m
A (sin
x) [
E] 0
2
2
a
a
h
a2
h2
E 2
n2
8a m
Набору собственных волн.функций ᴪ(x) соответствует набор собственных
значений Е, n = 1,2,3…- квантовое число

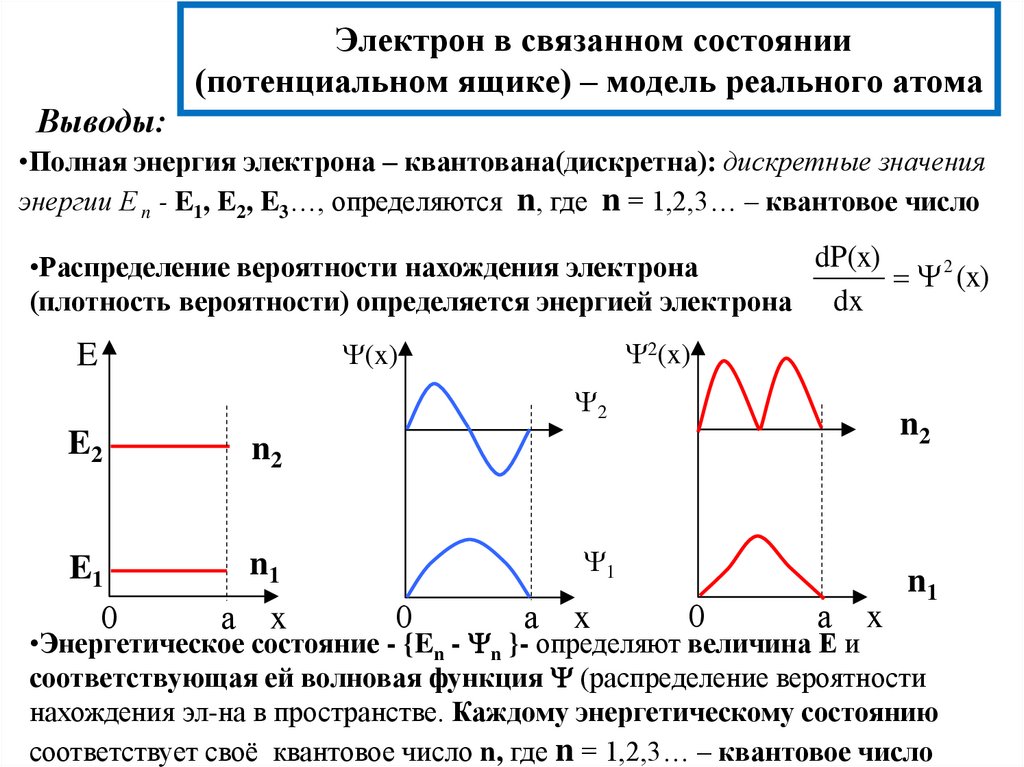
17. Электрон в связанном состоянии (потенциальном ящике) – модель реального атома

Выводы:
•Полная энергия электрона – квантована(дискретна): дискретные значения
энергии Е n - E1, E2, E3…, определяются n, где n = 1,2,3… – квантовое число
dP(x)
•Распределение вероятности нахождения электрона
2 (x)
(плотность вероятности) определяется энергией электрона dx
2(x)
(x)
E
2
E2
n2
E1
0
n1
а
x
n2
1
0
а
x
0
а
x
n1
•Энергетическое состояние - {En - n }- определяют величина Е и
соответствующая ей волновая функция (распределение вероятности
нахождения эл-на в пространстве. Каждому энергетическому состоянию
соответствует своё квантовое число n, где n = 1,2,3… – квантовое число

18. Электрон в трехмерном потенциальном ящике

Решение: электрон описывается
•Набором собственных волновых функций Ψ(х,y,z) в явном виде :
n y
8
n x
n
(x, y, z)
sin(
x) sin(
y) sin( z z)
a b c
a
b
c
где a,b,c – параметры потенц.ящика;
nx, ny, nz(1,2,3,4… – квантовые числа по осям x, y, z)
2
•Набором энергий: (**)
2
2
ny
h2 nx
nz
E
( 2 2 2 )
8m a
b
c
Выводы:
1. Энергия электрона дискретна (квантована). [Дискретность энергетических
состояний распространяется и на реальный атом].
2. Энергетическое состояние определяется набором целочисленных
параметров - трех квантовых чисел nx. ny, nz.

19. Вырожденные энергетические состояния

Одно значение энергии – при нескольких наборах квантовых чисел
(нескольких наборах волновых функций). Пример вырождения Е2, Е3, Е4
Если в (**) а = b = c
h2
Е, 8m a 2
h2
2
2
2
E
(n
n
n
x
y
z )
2
8m a
Е5 = 12
Е4 = 11
[2,2,2]
[3,1,1] [1,3,1] [1,1,3]
Е3 = 9
[2,2,1] [1,2,2] [2,1,2]
Е2 = 6
[2,1,1] [1,2,1] [1,1,2]
Е1 = 3
[1,1,1] (nx = 1, ny = 1, nz = 1; Е1 =12+12+12=3)
Трехкратная
степень
вырождения

20. Квантово-механическая модель атома. Основное состояние атома водорода [k=1/4πε0] - константа в з-не Кулона. Ур.Шредингера:

-ē
+ē
k e2
U
r
z
(x, y, z)
r
8 2 m
k e2
(x, y, z) 2 (E
) (x, y, z) 0
h
r
Основное состояние - Еmin
(r, , )
(r)
2
r
x
2 (r) 2 (r) 8 2 m
k e2
(E
) (r) 0
2
2
r
r r
h
r
y
x = r sin cos
y = r sin sin
z = r cos
(r) A e a r
Ψ(r) – волновая функция (собственная функция - конечна,
однозначна, непрерывна), явл. решением ур.Шредингера; а –
const, А – нормирующий коэффициент; Ψ(r)→0 при r→∞

21. Подставив собственную волн.функцию являющуюся решением в ур. Шредингера для сферически симметричной системы координат (ᴪ

Подставив собственную волн.функцию (r) A e a r
являющуюся решением в ур. Шредингера для сферически
симметричной системы координат (ᴪ зависит от r), можно
рассчитать Е – энергию электрона в атоме водорода в
основном состоянии:
2 2 m k 2 e4
E
h2
4 2 m k e 2
a
h2
ВЫВОД: Сходимость значений расчетной и
экспериментальной величин энергии Е электрона (-13,6
эВ в основном состоянии для атома водорода) –
квантово-механическая модель имеет право на
существование

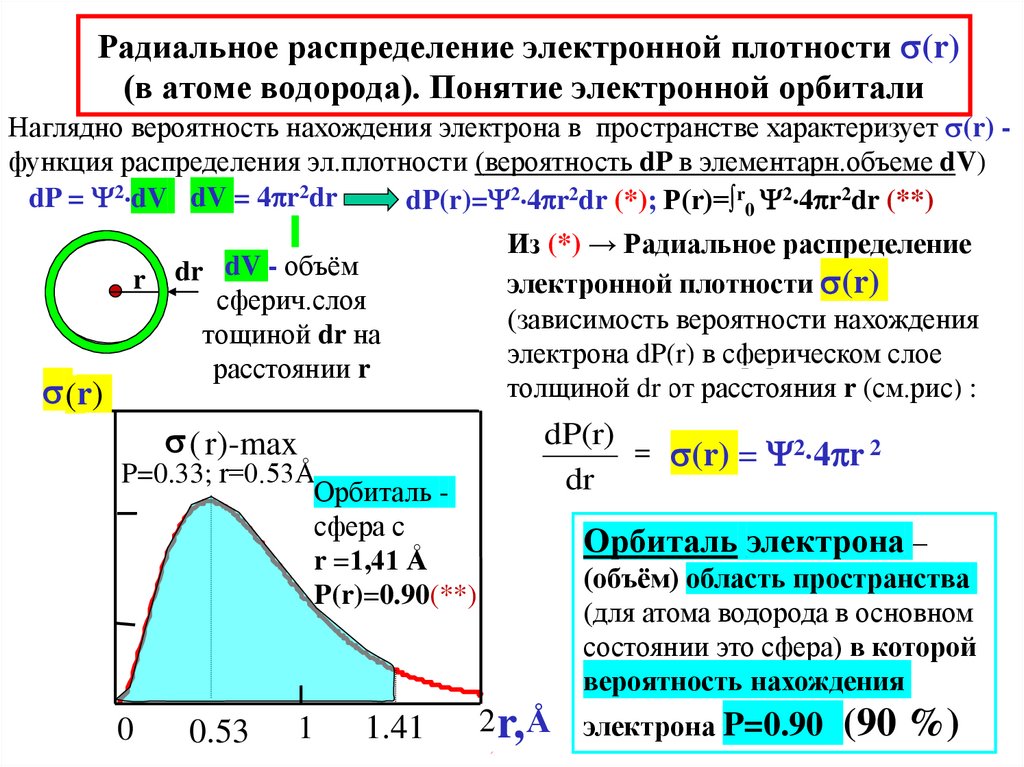
22. Радиальное распределение электронной плотности (r) (в атоме водорода). Понятие электронной орбитали

Радиальное распределение электронной плотности (r)
(в атоме водорода). Понятие электронной орбитали
Наглядно вероятность нахождения электрона в пространстве характеризует (r) функция распределения эл.плотности (вероятность dP в элементарн.объеме dV)
dP = 2 dV dV = 4 r2dr
dP(r)= 2 4 r2dr (*); P(r)=∫r0 2 4 r2dr (**)
(r)
dr dV - объём
сферич.слоя
тощиной dr на
расстоянии r
( r)-max
P=0.33; r=0.53Å
Орбиталь сфера с
r =1,41 Å
P(r)=0.90(**)
0
0.53
1
1.41
dP(r)
dr
=
r
Из (*) → Радиальное распределение
электронной плотности (r)
(зависимость вероятности нахождения
электрона dP(r) в сферическом слое
толщиной dr от расстояния r (см.рис) :
(r) = 2 4 r 2
Орбиталь электрона –
(объём) область пространства
(для атома водорода в основном
состоянии это сфера) в которой
вероятность нахождения
2 r, Å электрона P=0.90 (90 %)

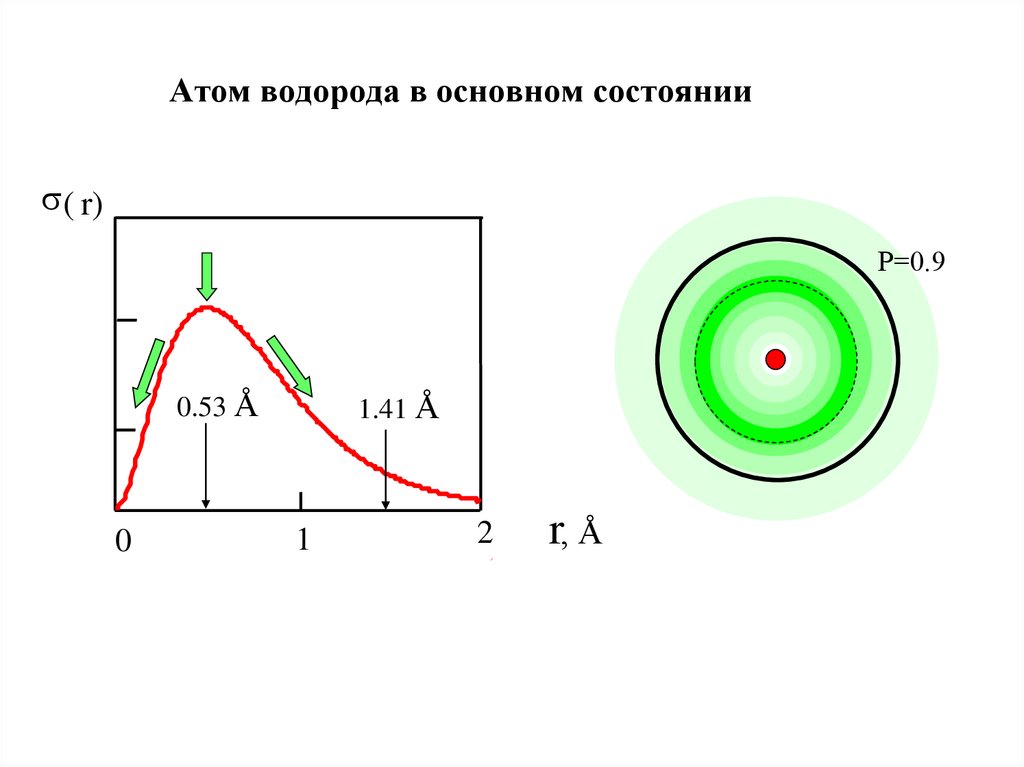
23. Атом водорода в основном состоянии

( r)
Р=0.9
0.53 Å
0
1.41 Å
1
2
r, Å

24. Возбужденные состояния атома водорода –более сложный вид волновых функций, чем (r)

Возбужденные состояния атома водорода –
более сложный вид волновых функций, чем (r)
Общий вид таких волновых функций - (r, , ). Используя метод разделения
переменных (r, , ) представляют в виде произведения функций R(r) Y( , )
R(r)n, l -функция радиального распределения электронной плотности в
явном виде (получают при решении ур. Шреденгера) содержит n и l
Y( , )l,m -функция углового распределения электронной плотности в
явном виде (получают при решении ур. Шреденгера) содержит l и m, где
n, l, m - целочисленные параметры волновых функций R(r)n, l и Y( , )l,m в
явном виде – наз. квантовыми числами
Квант.числа определяют набор собственных волн.функций (решений
ур.Шредингера) и соответствующий им набор энергетических состояний{En n,l,m} в атоме водорода
Квантовые числа:
главное – n = 1,2,3,4…
орбитальное – l = 0,1,2,3...(n -1)
магнитное – m = -l, (-l+1),...,0,...,(+l–1), +l
спиновое – ms =±1/2 (1933 г.) Поль Дирак, модель Уленбека и Гаудсмита

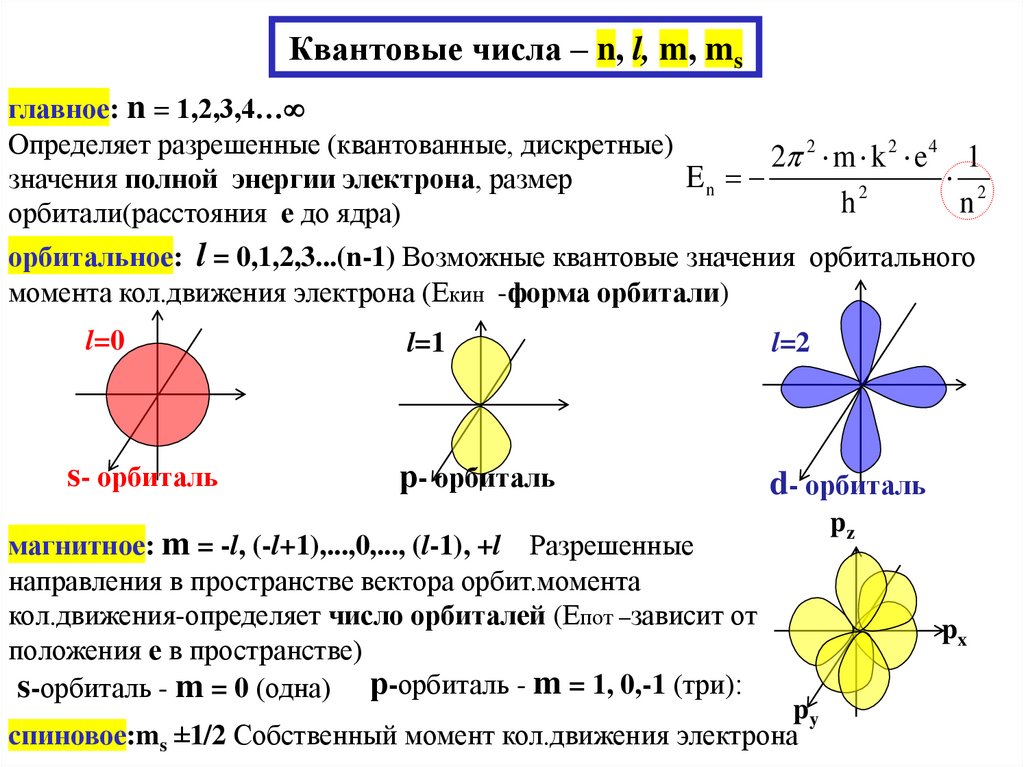
25. Квантовые числа – n, l, m, ms

главное: n = 1,2,3,4…
Определяет разрешенные (квантованные, дискретные)
2 2 m k 2 e 4 1
En
2
значения полной энергии электрона, размер
2
h
n
орбитали(расстояния е до ядра)
орбитальное: l = 0,1,2,3...(n-1) Возможные квантовые значения орбитального
момента кол.движения электрона (Екин -форма орбитали)
l=0
l=1
l=2
s- орбиталь
р- орбиталь
d- орбиталь
магнитное: m = -l, (-l+1),...,0,..., (l-1), +l Разрешенные
направления в пространстве вектора орбит.момента
кол.движения-определяет число орбиталей (Епот –зависит от
положения е в пространстве)
s-орбиталь - m = 0 (одна) р-орбиталь - m = 1, 0,-1 (три):
py
cпиновое:ms ±1/2 Собственный момент кол.движения электрона
pz
px

26.

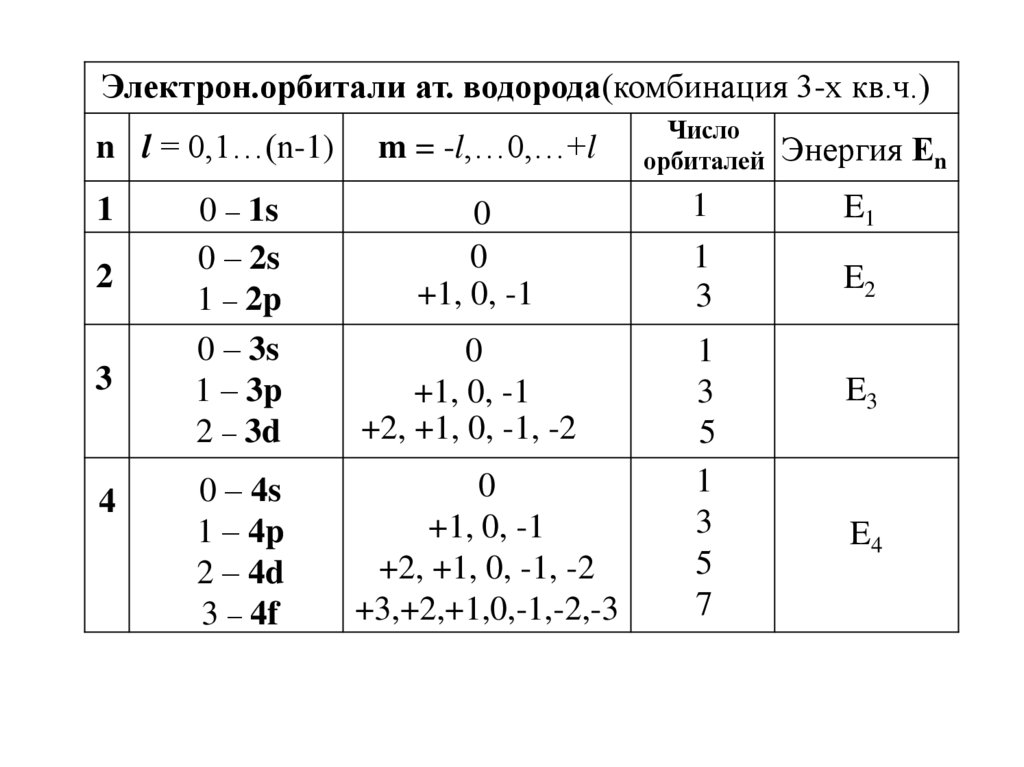
Электрон.орбитали ат. водорода(комбинация 3-х кв.ч.)
Число
орбиталей Энергия Еn
n l = 0,1…(n-1)
m = -l,…0,…+l
0 – 1s
0 – 2s
1 – 2p
0 – 3s
1 – 3p
2 – 3d
0
0
+1, 0, -1
1
E1
1
3
E2
0
+1, 0, -1
+2, +1, 0, -1, -2
0 – 4s
1 – 4p
2 – 4d
3 – 4f
0
+1, 0, -1
+2, +1, 0, -1, -2
+3,+2,+1,0,-1,-2,-3
1
3
5
1
3
5
7
1
2
3
4
E3
E4

27. Энергетическая диаграмма орбиталей в атоме водорода

Е
n=4
n=3
n=2
n=1
4s
4p
4d
3s
3p
3d
2s
2p
4f
1s
E1s < E2s = E2p< E3s = E3p = E3d < E4s = E4p = E4d = E4f < E5s …
(вырождение энергии по орбит.кв.ч. l и по магн.кв.ч.m . Энергия
Е электрона зависит только от значения главного кв.ч. n)

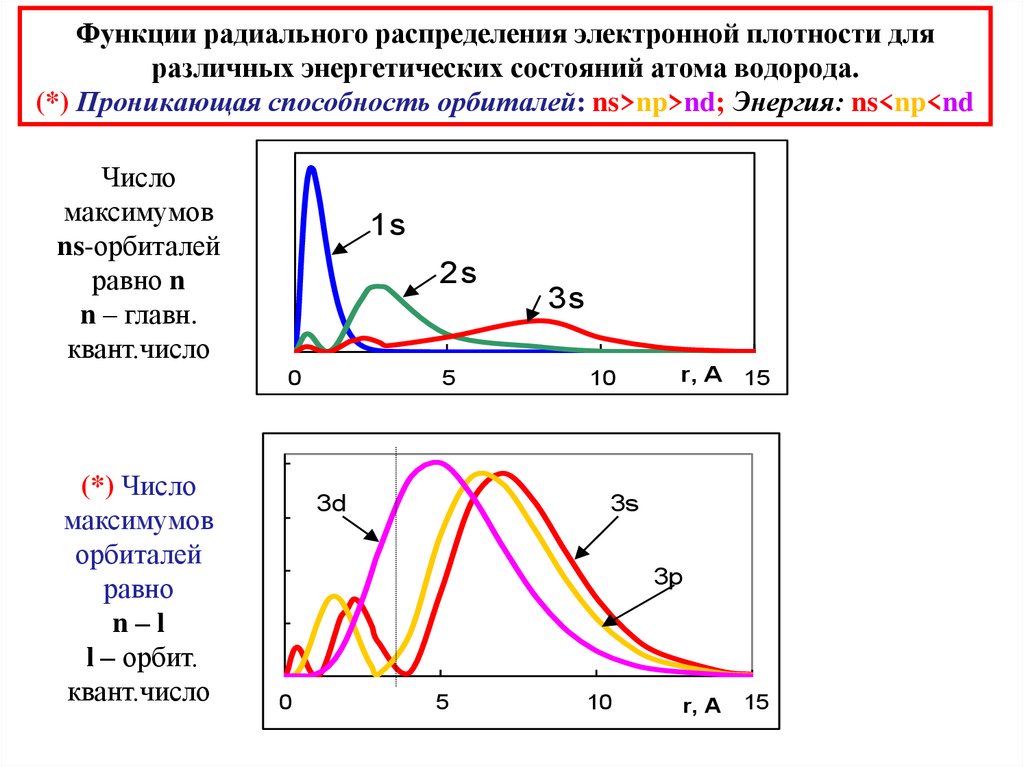
28. Функции радиального распределения электронной плотности для различных энергетических состояний атома водорода. (*) Проникающая

способность орбиталей: ns>np>nd; Энергия: ns<np<nd
Число
максимумов
ns-орбиталей
равно n
n – главн.
квант.число
1s
2s
0
(*) Число
максимумов
орбиталей
равно
n–l
l – орбит.
квант.число
5
3d
3s
10
r, A 15
3s
3p
0
5
10
r, A
15

29. 1.7 Многоэлектронный атом (одноэлектронное приближение - водородоподобная система, описание многоэлектронного атома похоже на

описание атома
водорода). Электрон в поле эффективного заряда Zэ
Z
э
+Z
Zэ = Z - n,l
Z – заряд ядра
Zэ - эффективный заряд ядра
n,l - константа экранирования
ē
-(Z-1)
Атом
Z
n,l
Zэ=Z -
H
1
0
1
He Li Be
B
C
2
3
4
5
6
0.3 2.70 2.05 2.40 2.75
1.7 1.30 1.95 2.60 3.25

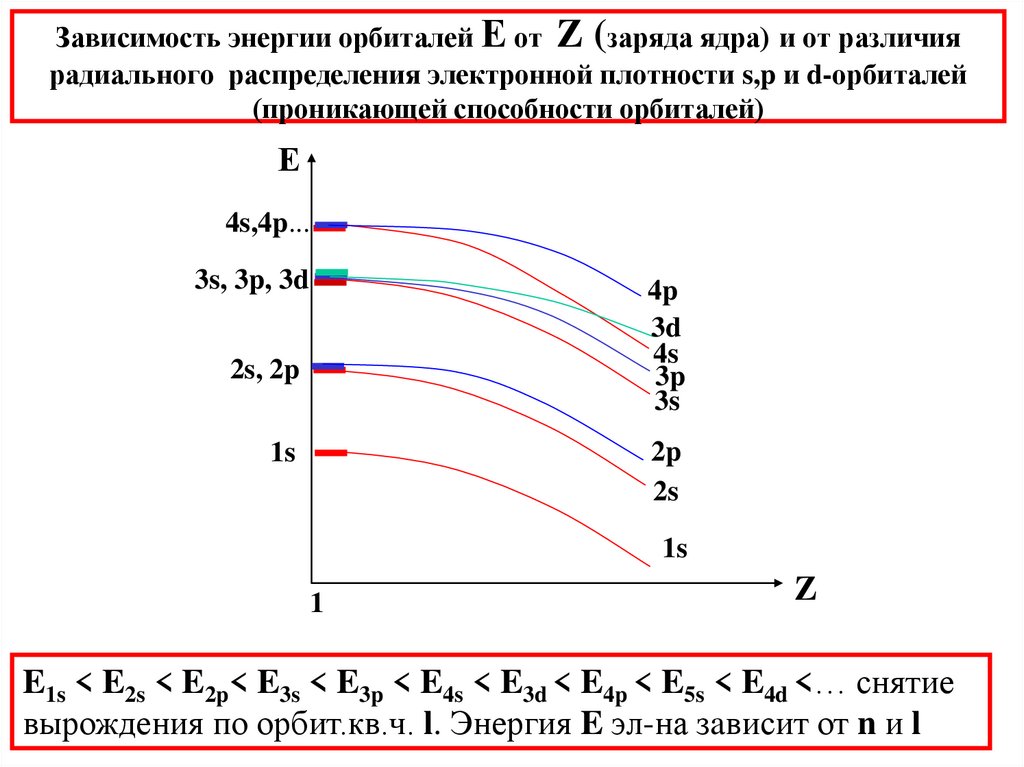
30. Зависимость энергии орбиталей Е от Z (заряда ядра) и от различия радиального распределения электронной плотности s,p и

d-орбиталей
(проникающей способности орбиталей)
Е
4s,4p...
3s, 3p, 3d
4p
3d
4s
3p
3s
2s, 2p
2p
2s
1s
1s
1
Z
E1s < E2s < E2p< E3s < E3p < E4s < E3d < E4p < E5s < E4d <… снятие
вырождения по орбит.кв.ч. l. Энергия E эл-на зaвисит от n и l

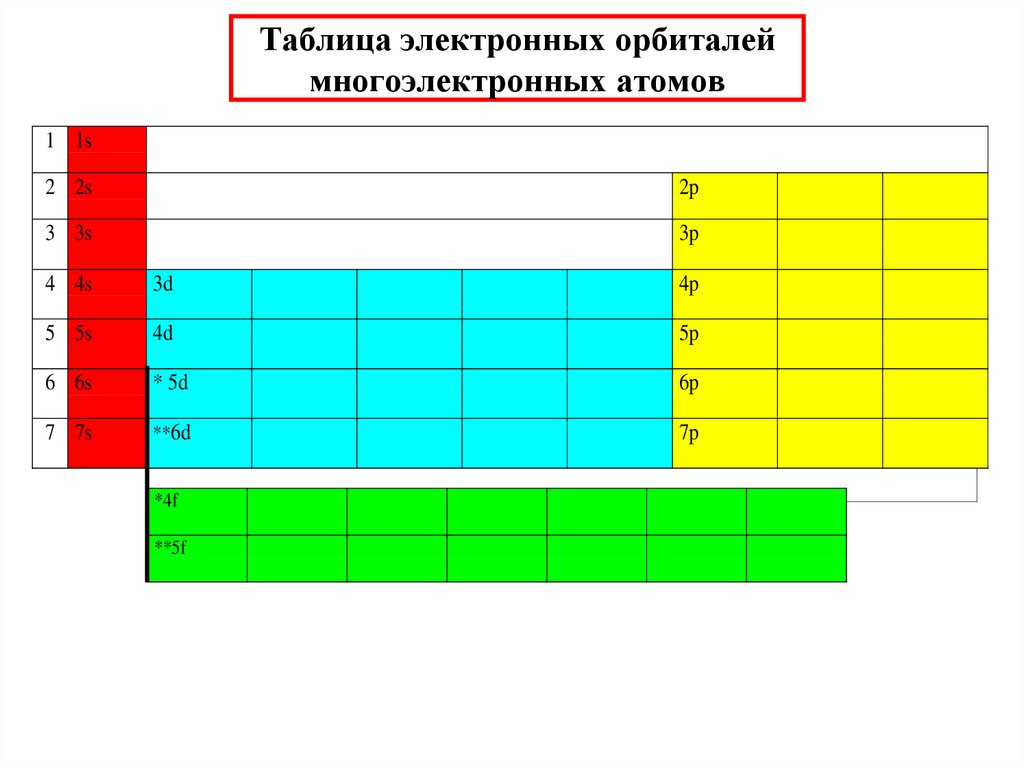
31. Таблица электронных орбиталей многоэлектронных атомов

1 1s
2 2s
2p
3 3s
3p
4 4s
3d
4p
5 5s
4d
5p
6 6s
* 5d
6p
7 7s
**6d
7p
*4f
**5f

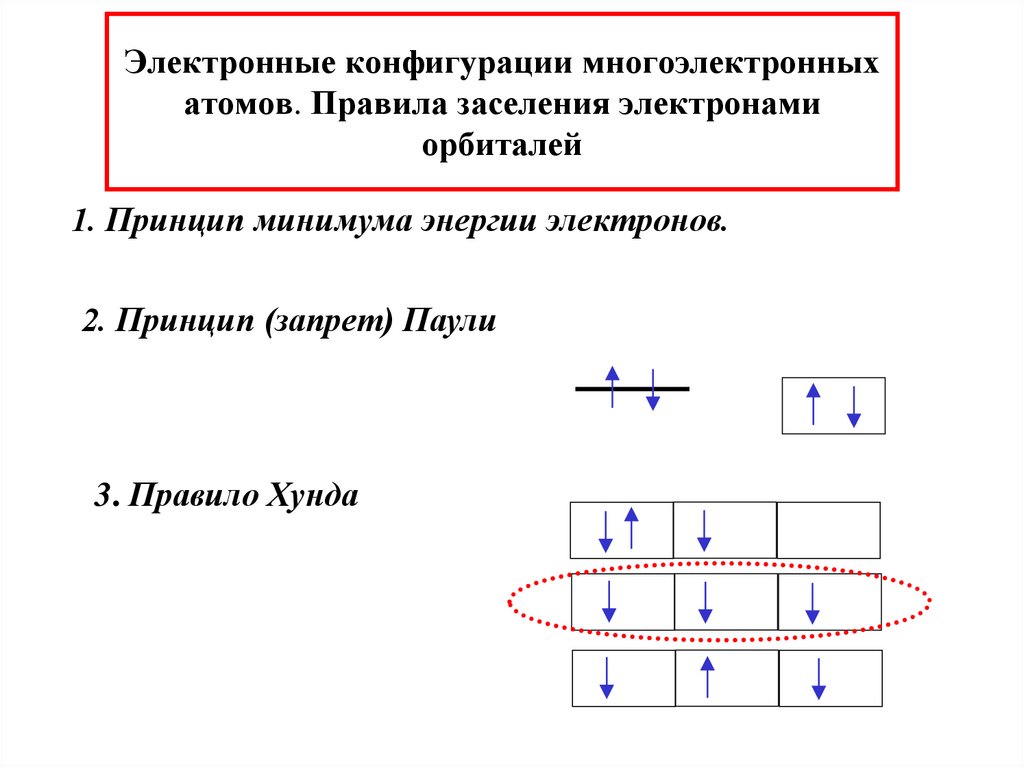
32. Электронные конфигурации многоэлектронных атомов. Правила заселения электронами орбиталей

1. Принцип минимума энергии электронов.
2. Принцип (запрет) Паули
3. Правило Хунда

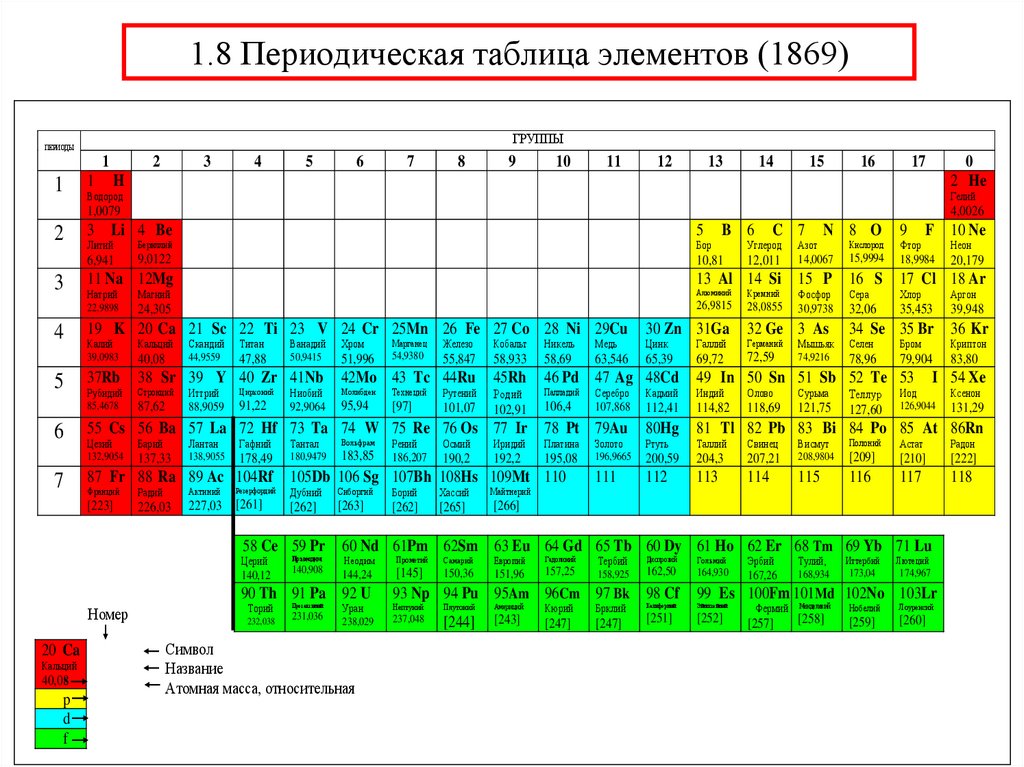
33. 1.8 Периодическая таблица элементов (1869)

ГРУППЫ
ПЕРИОДЫ
1 1s 1
2
1
H
1
2 2sВодород
1,0079
Be
2 3 Li 4Бериллий
3 3sЛитий
9,0122
6,941
3
4
5
6
7
8
9
10
11
12
5
Ванадий
50,9415
Железо
Кобальт
Никель
Медь
Цинк
54,9380
55,847
58,933
58,69
63,546
65,39
Sr 39 Y 40 Zr 41Nb 42Mo 43 Tc 44Ru
5 37Rb 38
Стронций
Технеций
Ниобий
Рутений
6 6sРубидий
*
5dИттрий
85,4678
87,62
[97]
88,9059 91,22
92,9064 95,94
101,07
45Rh
46 Pd 47 Ag 48Cd
Родий
Палладий
102,91
106,4
Цирконий
Молибден
Ba 57 La 72 Hf 73 Ta 74 W 75 Re 76 Os 77 Ir
6 55 Cs 56
Барий**6d
Лантан
Гафний
Тантал
Рений
Осмий
Иридий
7 7sЦезий
132,9054 137,33
138,9055 178,49
180,9479 183,85
186,207 190,2
192,2
Вольфрам
87 Fr 88 Ra 89 Ac 104Rf
Дубний
Сиборгий
Борий
Хассий
Майтнерий
*4f 227,03
[261]
[262]
[263]
[262]
[265]
[266]
**5f
Церий
58 Ce 59 Pr
140,12
Празеодим
140,908
Кальций
40,08s
p
d
f
Азот
Кислород
Фтор
Неон
14,0067
15,9994
18,9984
20,179
15 P 16 S
232,038
Протактиний
231,036
72,59
Мышьяк
74,9216
17 Cl 18 Ar
Хлор
Аргон
35,453
39,948
34 Se 35 Br 36 Kr
Селен
Бром
Криптон
78,96
79,904
83,80
49 In 50 Sn 51 Sb 52 Te 53
Кадмий
6pИндий
107,868 112,41 114,82
Олово
Сурьма
Теллур
118,69
121,75
127,60
I 54 Xe
Иод
126,9044
80Hg
Ртуть
7pТаллий
200,59 204,3
Свинец
Висмут
208,9804
Полоний
Астат
Радон
207,21
[209]
[210]
[222]
111
112
114
115
116
117
118
195,08
Неодим
Прометий
Самарий
Европий
Гадолиний
[145]
150,36
151,96
157,25
Символ
Название
Атомная масса, относительная
Тербий
158,925
81 Tl 82 Pb 83 Bi 84 Po 85 At 86Rn
113
Диспрозий
Гольмий
162,50
Эрбий
164,930
167,26
93 Np 94 Pu 95Am 96Cm 97 Bk 98 Cf
Нептуний
237,048
Плутоний
Америций
[244]
[243]
131,29
Золото
196,9665
144,24
Уран
238,029
Ксенон
Платина
60 Nd 61Pm 62Sm 63 Eu 64 Gd 65 Tb 60 Dy 61 Ho 62 Er 68 Tm 69 Yb 71 Lu
90 Th 91 Pa 92 U
Торий
F 10 Ne
78 Pt 79Au
105Db 106 Sg 107Bh 108Hs 109Mt 110
Резерфордий
Актиний
Серебро
5pГаллий
69,72
9
12,011
Германий
Марганец
20 Ca
0
2 He
Углерод
32 Ge 3 As
51,996
Номер
N 8 O
30 Zn 31Ga
Хром
226,03
C 7
Алюминий
Титан
4d Скандий
44,9559
47,88
[223]
17
4,0026
B 6
13 Al 14 Si
40,08
Радий
16
Фосфор
Сера
4p26,9815 Кремний
28,0855 30,9738 32,06
Кальций
Франций
15
Гелий
3pБор
10,81
19 K 20 Ca 21 Sc 22 Ti 23 V 24 Cr 25Mn 26 Fe 27 Co 28 Ni 29Cu
7
14
2p
3 11 Na 12Mg
Магний
4 4sНатрий
3d
22,9898
24,305
4
5 5sКалий
39,0983
13
Кюрий
Брклий
[247]
[247]
Тулий,
168,934
Иттербий
Лютеций
173,04
174,967
99 Es 100Fm 101Md 102No 103Lr
Калифорний
Эйнштейний
[251]
[252]
Фермий
[257]
Менделевий
Нобелий
Лоуренсий
[258]
[259]
[260]

34. Физико-химические характеристики атома Ковалентный радиус ( RA = rсв /2) и радиус иона

R A R A0 R A
Частица
Радиус, Å
Частица
Радиус, Å
Na0
1.54
Sr0
1.91
Na+
1.02
Sr+2
1.18
Cl0
0.99
S0
1.02
Cl1.81
S-2
1.84

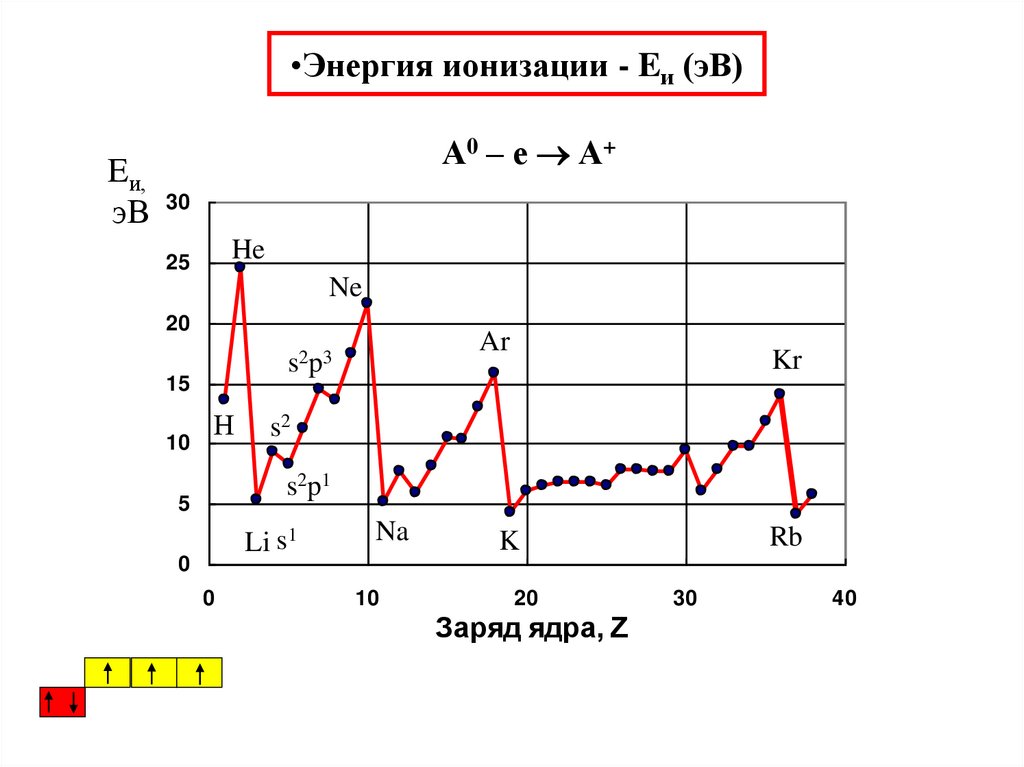
35. Энергия ионизации - Eи (эВ)

•Энергия ионизации - Eи (эВ)
А0 – е А+
Eи,
эВ 30
He
25
Ne
20
15
10
Ar
s2 p 3
Н
Kr
s2
s2 p 1
5
Li s1
0
0
Na
10
Rb
K
20
Заряд ядра, Z
30
40

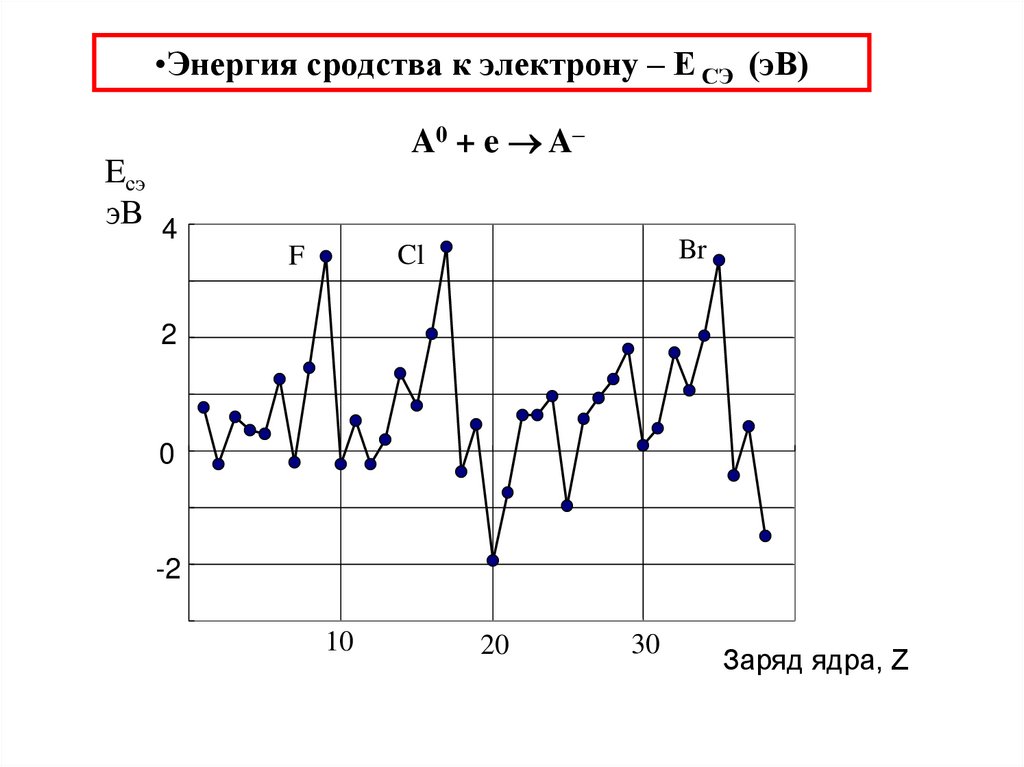
36. Энергия сродства к электрону – Е СЭ (эВ)

•Энергия сродства к электрону – Е СЭ (эВ)
A0 + e A–
Eсэ
эВ 4
Br
Cl
F
2
0
-2
10
20
30
Заряд ядра, Z

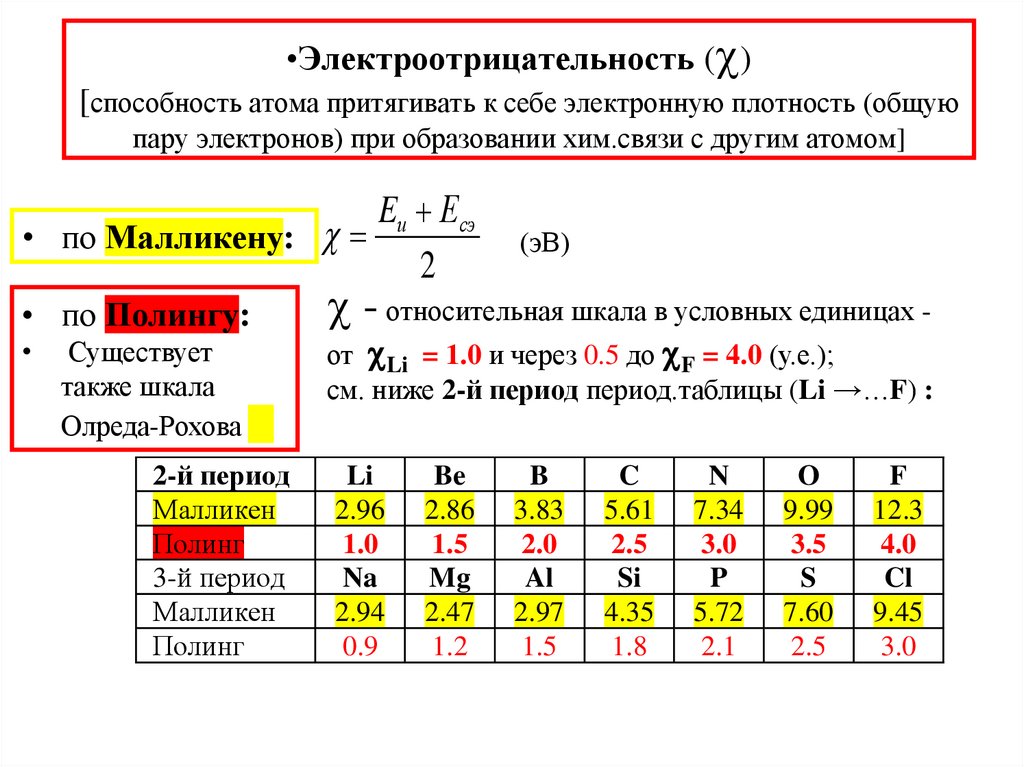
37. Электроотрицательность () [способность атома притягивать к себе электронную плотность (общую пару электронов) при образовании

•Электроотрицательность ( )
[способность атома притягивать к себе электронную плотность (общую
пару электронов) при образовании хим.связи с другим атомом]
Eи Есэ
• по Малликену:
2
• по Полингу:
Существует
также шкала
Олреда-Рохова
2-й период
Малликен
Полинг
3-й период
Малликен
Полинг
(эВ)
- относительная шкала в условных единицах -
от Li = 1.0 и через 0.5 до F = 4.0 (у.е.);
см. ниже 2-й период период.таблицы (Li →…F) :
Li
2.96
1.0
Na
2.94
0.9
Be
2.86
1.5
Mg
2.47
1.2
B
3.83
2.0
Al
2.97
1.5
C
5.61
2.5
Si
4.35
1.8
N
7.34
3.0
P
5.72
2.1
O
9.99
3.5
S
7.60
2.5
F
12.3
4.0
Cl
9.45
3.0