Защита курсовой работы по теме: «Разделение движений в системах с разрывными характеристиками. Качение приторможенного колеса»

1. Защита курсовой работы по теме «Разделение движений в системах с разрывными характеристиками. Качение приторможенного колеса»

Презентацию выполнил: Кизяев Ф.И
Группа: С-12б-21

2. Постановка задачи

Рассматривается процесс торможения колеса экипажа на наклонной плоскости в простейшей
постановке. Колесо - однородный абсолютно твёрдый круглый диск. Торможение осуществляется
силами кулонова трения в точке контакта колеса и плоскости и тормозной колодки. В зависимости
от сочетания динамических параметров и начальных условий движения качение может происходить
как с проскальзыванием в точке контакта, так и при его отсутствии, с блокировкой и без блокировки
угловых движений. С помощью асимптотических методов разделения движений в системах с
разрывными характеристиками требуется проследить характер развития различных динамических
процессов.

3. Исследование характера процесса торможения колеса

Записав теорему о движении центра масс колеса и теорему об изменении кинетического момента
колеса в движении относительно центра масс (1) и приведя к безразмерному нормализованному виду
(2), проведем исследование характера процесса торможения колеса
(1)
(2)
Решая дифференциальные уравнения, проверим возможность полной остановки диска. И как видно
на графике из решения для остановки колеса необходимые значения силы трения в точке
контакта превышают по модулю 1, что физически неосуществимо . Следовательно, диск не
может быть остановлен .

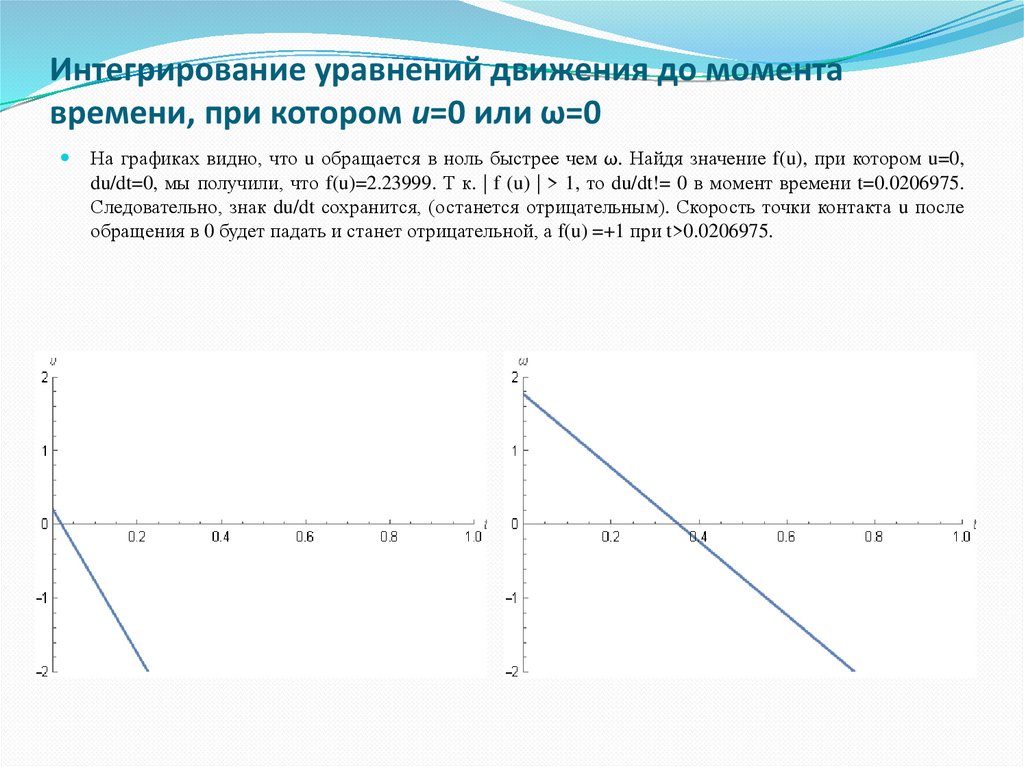
4. Интегрирование уравнений движения до момента времени, при котором u=0 или ω=0

На графиках видно, что u обращается в ноль быстрее чем ω. Найдя значение f(u), при котором u=0,
du/dt=0, мы получили, что f(u)=2.23999. Т к. | f (u) | > 1, то du/dt!= 0 в момент времени t=0.0206975.
Следовательно, знак du/dt сохранится, (останется отрицательным). Скорость точки контакта u после
обращения в 0 будет падать и станет отрицательной, а f(u) =+1 при t>0.0206975.

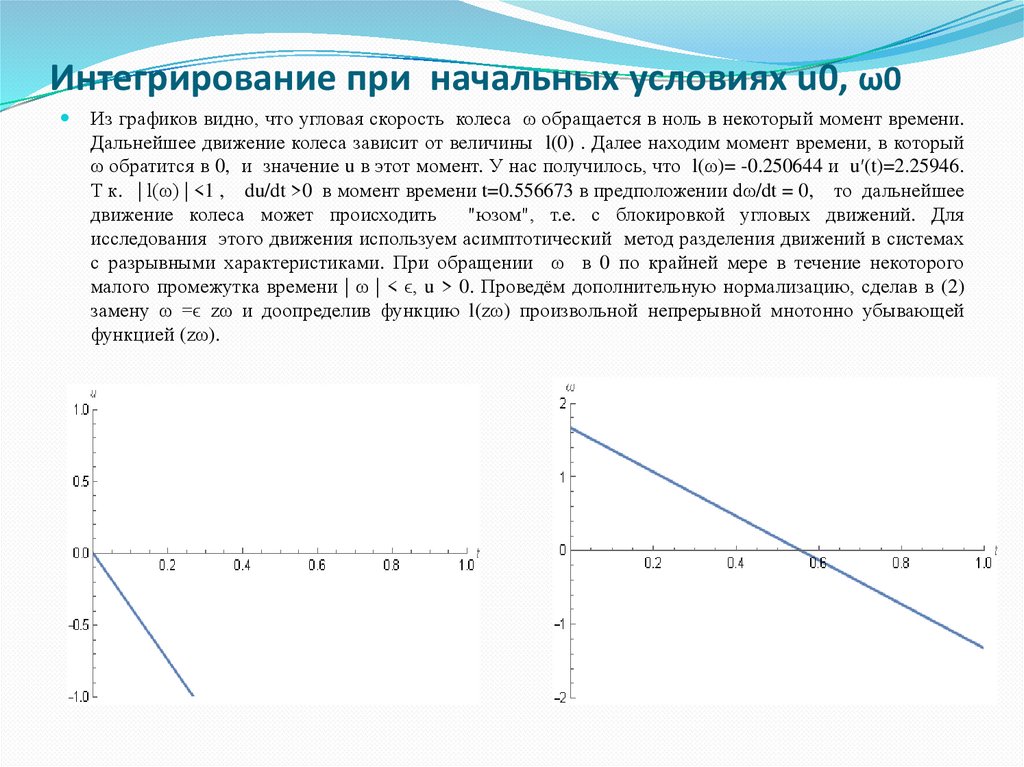
5. Интегрирование при начальных условиях u0, ω0

Из графиков видно, что угловая скорость колеса ω обращается в ноль в некоторый момент времени.
Дальнейшее движение колеса зависит от величины l(0) . Далее находим момент времени, в который
ω обратится в 0, и значение u в этот момент. У нас получилось, что l(ω)= -0.250644 и u′(t)=2.25946.
Т к. | l(ω) | <1 , du/dt >0 в момент времени t=0.556673 в предположении dω/dt = 0, то дальнейшее
движение колеса может происходить
"юзом", т.е. с блокировкой угловых движений. Для
исследования этого движения используем асимптотический метод разделения движений в системах
с разрывными характеристиками. При обращении ω в 0 по крайней мере в течение некоторого
малого промежутка времени | ω | < ϵ, u > 0. Проведём дополнительную нормализацию, сделав в (2)
замену ω =ϵ zω и доопределив функцию l(zω) произвольной непрерывной мнотонно убывающей
функцией (zω).

6. Исследование вырожденной системы уравнений и допустимости перехода к вырожденной системе

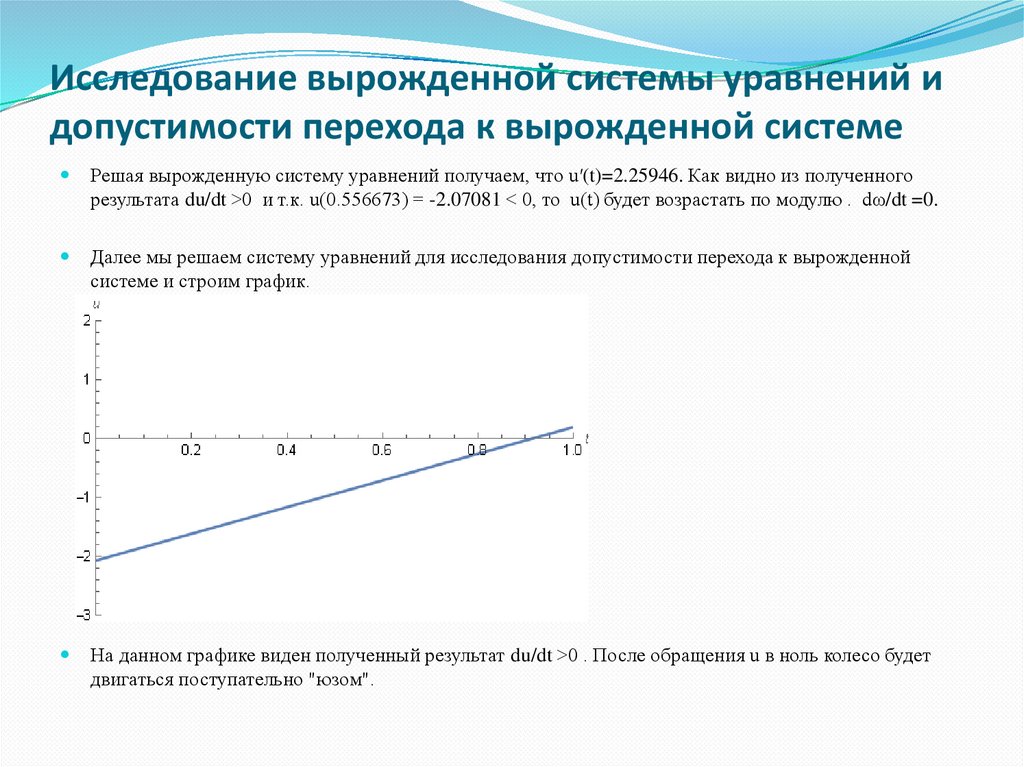
Решая вырожденную систему уравнений получаем, что u′(t)=2.25946. Как видно из полученного
результата du/dt >0 и т.к. u(0.556673) = -2.07081 < 0, то u(t) будет возрастать по модулю . dω/dt =0.
Далее мы решаем систему уравнений для исследования допустимости перехода к вырожденной
системе и строим график.
На данном графике виден полученный результат du/dt >0 . После обращения u в ноль колесо будет
двигаться поступательно "юзом".

7. Спасибо за внимание