Похожие презентации:
Введение. Механика. Элементы кинематики. (лекция № 1)
1. ЛЕКЦИЯ № 1 Введение. Механика. Элементы кинематики.
1431
2. ВОПРОСЫ Введение. 1. Механическое движение. Система отсчёта. Средняя и мгновенная скорости. 2. Ускорение. Уравнение кинематики
поступательного равнопеременногодвижения (вывод).
3. Движение материальной точки по
окружности. Угловая скорость и
угловое ускорение.
143
2
3. Введение
1433
4. Физика это наука изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи
и законы её движений.Понятия физики и её законы лежат в
основе всего естествознания. Физика
относится к точным наукам и изучает
количественные закономерности
явлений.
143
4
5. В методах физических исследований выделяют четыре этапа: 1) Опыт – наблюдение исследуемого явления в точно контролируемых
условиях;143
5
6. Для объяснения данных привлекаются гипотезы. 2) Гипотеза – это научное предположение, выдвигаемое для объяснения какого-либо
факта илиявления и требующее
доказательства;
143
6
7. Для проверки гипотезы ставят эксперимент. 3) Эксперимент – создание явления, которое естественно в природе не наблюдается, для
отделения отнекоторых субъективных условий
или факторов;
143
7
8. Если гипотеза прошла успешную проверку, она превращается в теорию или закон. 4) Физическая теория представляет собой систему
основных идей,обобщающих данные и отражающих
объективные закономерности
природы.
143
8
9. Основные этапы развития физики: 1) Атомарное строение, законы статики – античность и средние века; 2) Создание классической
механики– 17 век, Галилей, Ньютон;
3) Создание в 20 веке квантовой
теории и теории относительности
(излучение абсолютно чёрного тела
и распространение света в среде);
4) Проблемы физики на сегодняшний
день.
143
9
10. Проблемы физики: 1) элементарные частицы (кварки и глюоны); 2) астрофизика (чёрные дыры, квазары и т.д.); 3) физика ядра
(термоядерныйсинтез);
4) квантовая электроника (γ-лазеры);
5) физика твёрдого тела
(сверхпроводимость).
143
10
11. Роль физики в развитии техники: 1) Развитие термодинамики дало промышленности тепловые машины; 2) Электродинамика –
электродвигатели;3) Ядерная физика – АЭС.
143
11
12. Физика и моделирование. Физика служит для описания явлений, для предсказания результата явлений, т.е. можно сказать, что
физика, на основетеорий и законов, строит
математические модели явлений,
протекающих в природе.
143
12
13. Даже простейший процесс, такой как прямолинейное равномерное движение, описывается с помощь математической модели: S = V * t.
Эта математическая модель (илифизическая формула) позволяет по
двум заданным величинам найти
третью величину.
143
13
14. Другой пример: задача о движении двух тел: с помощью формул движения и взаимодействия мы можем сказать где они будут находиться
в некоторый моментвремени. Здесь будет использовано
формул больше, но это тоже модель
некоторого явления или процесса.
143
14
15. Иногда математические формулы получаются настолько сложные, что их аналитически решить не возможно (например, задача о движении
трёх и более небесныхтел), тогда на помощь приходит
Электронная Вычислительная
Машина и специальные методы
расчёта. Но это тоже будет
некоторая математическая модель.
143
15
16. Также, с усложнением экспериментов компьютеру отводится задача управления, сбора и обработки данных.
14316
17.
14317
18. Вопрос № 1. Механическое движение. Система отсчёта. Материальная точка. Траектория. Перемещение и путь. Средняя и мгновенная
скорости.143
18
19. Кинематика изучает законы движения тел. Материальная точка – модель тела, размерами которого можно пренебречь, по сравнению с
расстояниями в задаче.Механическое движение –
изменение положения тела с
течением времени относительно
других тел.
143
19
20. Система отсчёта – тело отсчёта, система координат, часы. Декартова система отсчёта в Евклидовом пространстве (пространство, в
которомвыполняются аксиомы геометрии).
Положение тела задаётся через
радиус-вектор r или через
координаты (x, y, z) (численно равны
проекциям радиус-вектора).
143
20
21.
14321
22. Здесь i, j, k, – единичные ортогональные вектора, направленные вдоль осей x, y, z, соответственно. Вектор r, также может быть
представлен в видепроизведения величины | r | (модуль
вектора) и направления – er
(единичный вектор, который задаёт
направление).
143
22
23. Траектория – линия, вдоль которой движется тело. Путь – расстояние, которое проходит тело по траектории. Скалярная величина,
которая характеризуетсятолько величиной – модулем.
Перемещение – вектор,
направленный из начальной точки в
конечную, характеризуется модулем
и направлением.
143
23
24. Так как тело может менять положение, то положение задают в зависимости от времени: векторно r = r (t); или скалярно x = x(t); y
= y(t);z = z(t).
143
24
25.
14325
26. Изменение положения с течением промежутка времени Δt характеризуют скоростью. Средняя скорость (по пути и по перемещению,
соответственно)S
r
ср
ср
t
t
143
26
27. Мгновенная скорость (по пути и по перемещению, соответственно) точка над символом обозначает производную по времени.
Мгновенная скорость (по пути и поперемещению, соответственно)
S dS
м lim
S,
t 0
t dt
r dr
м lim
r
t 0
t dt
точка над символом обозначает
производную по времени.
143
27
28. Здесь dS, dr, dt – дифференциал, очень малое изменение величины – приращение (ещё может быть очень малая доля некоторой
величины),dS / dt, dr / dt – производная, она
показывает изменение одной
величины в зависимости от другой.
143
28
29.
14329
30. Вопрос № 2. Ускорение. Тангенциальное и нормальное ускорения. Уравнение кинематики поступательного равнопеременного движения
(вывод).143
30
31. Изменение скорости характеризуют ускорением. Среднее ускорение
vaср
ср
t
t
143
31
32. Мгновенное ускорение (по пути и по перемещению, соответственно)
d d Saм lim
2 S,
t 0
t dt dt
2
d d r
aм lim
2 r
t 0
t
dt dt
2
143
32
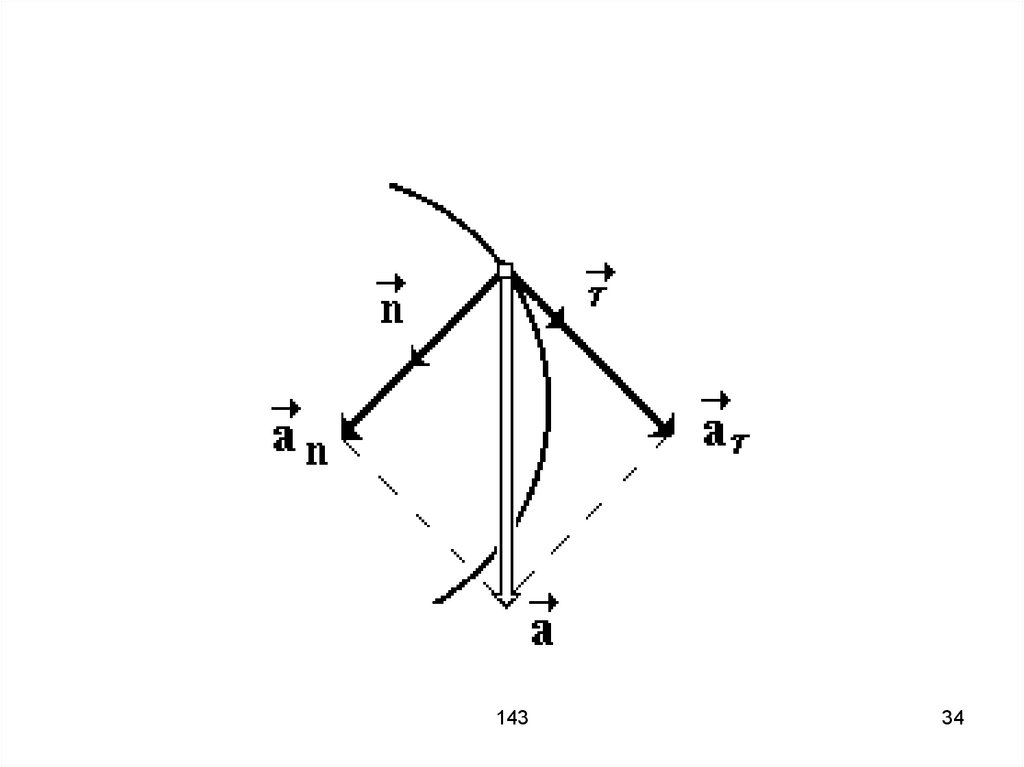
33. Выделим на траектории бесконечно малый участок dS, который можно заменить дугой окружности с радиусом R. Отметим также вектора
τ – единичный вектор, направленныйпо касательной к траектории, n –
единичный вектор, направленный по
радиусу R к центру окружности.
143
33
34.
14334
35. Скорость представим в виде тогда ускорение можно записать следующим образом
d da
a an
dt
dt
143
35
36. Нормальное ускорение, направлено по нормали к траектории, изменяет направление движения Тангенциальное ускорение, направлено по
Нормальное ускорение, направленопо нормали к траектории, изменяет
направление движения
2
an n
R
Тангенциальное ускорение,
направлено по касательной к
траектории, изменяет модуль
скорости
d
a
dt
143
36
37. Рассмотрим на рисунке два подобных треугольника, с катетами R, ΔS и τ, Δτ (или ʋ, Δʋ).
14337
38.
τʋ τ
Δτ Δʋ
ΔS
n
R
143
38
39. В пределе Δt → 0 Поделим на промежуток времени dt и преобразуем или
dτ dSτ S
В пределе Δt → 0
τ
R
τ
R
Поделим на промежуток времени dt
и преобразуем
dτ dS
dτ
dS τ
τ
τ
τdt Rdt
dt
dt R
R R
или
dτ
an ; a n n
R
R
dt
2
2
143
39
40. Вычисление пути Равномерное движение Если движение задано про проекциям
Вычисление путиРавномерное движение
a 0 const
S r r t S t
Если движение задано про
проекциям
2
2
2
r x y z
r x y z
143
40
41. Аналогично вычисляем скорость
x y z2
x
2
y
143
2
z
41
42. Равноускоренное движение Весь путь разбивают на множество участков, на которых скорость можно считать постоянной (за малый
Равноускоренное движениеa const 0 at
Весь путь разбивают на множество
участков, на которых скорость можно
считать постоянной (за малый
промежуток времени изменением
скорости можно пренебречь)
143
42
43. Полный путь или перемещение получаем сложением этих малых участков Чем меньше промежутки времени, тем точнее расчёт.
Полный путь или перемещениеполучаем сложением этих малых
участков
r t
Чем меньше промежутки времени,
тем точнее расчёт.
143
43
44. Переходим к пределу
r lim t t dtt2
t 0
t1
2 t
at
0 at dt 0t
2 t
t
t2
1
143
2
1
44
45. Положим начальный момент времени равным нулю и добавим начальное положение r0 или S0 Это закон кинематики равноускоренного
Положим начальный моментвремени равным нулю и добавим
начальное положение r0 или S0
2
at
r r0 0t
2
2
at
S S 0 0t
2
Это закон кинематики
равноускоренного движения
143
45
46. Вычислить ускорение можно следующими способами (аналогично скорости и перемещению)
a ax a y az an aτa
2
ax
2
ay
143
2
az
2
an
2
aτ
46
47.
14347
48. Вопрос № 3. Движение материальной точки по окружности. Угловая скорость и угловое ускорение. Уравнения кинематики вращательного
движения.Связь между линейными и угловыми
характеристиками движения.
143
48
49. Вращательное движение Вращательным движением абсолютно твердого тела называют движение, при котором все его точки описывают
окружности, лежащие впараллельных плоскостях, а центры
их лежат на оси вращения.
143
49
50.
14350
51.
14351
52. Вращательное движение характеризуется углом поворота φ, угловой скорость вращения ω, угловым ускорением ε
dω lim
t 0 t
dt
ω dω
ε lim
ω
t 0 t
dt
143
52
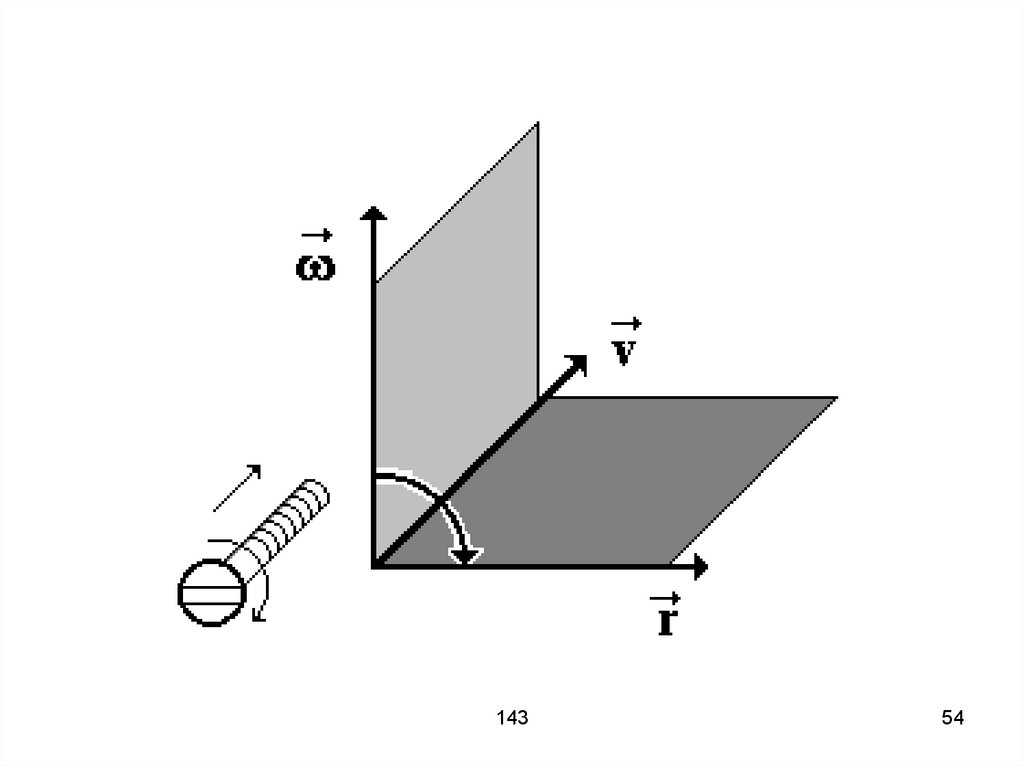
53. Вектор ω направляют вдоль оси вращения согласно правилу правого буравчика
ω r143
53
54.
14354
55. Вектора ω и ε направлены одинаково, если вращение ускоренное, вектора ω и ε направлены в разные стороны, если вращение
замедленное.143
55
56.
14356
57. Связь величин Закон кинематики равнопеременного вращательного движения
Связь величинaτ ε r ω r S r
Закон кинематики равнопеременного
вращательного движения
2
εt
0 ω 0t
2
143
57
58. Так же, для описания вращательного движения используют частоту (количество оборотов за 1 секунду) и период (время одного
полногооборота)
1
ν
T
1
T
ν
143
58
59. Циклическая частота она же угловая скорость вращения – количество оборотов за 2π секунды
ω 2π ν2π
ω
T
143
59
60. Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся телом, остаётся параллельной
самой себе.Вращательное движение – все точки
тела движутся по окружностям,
центры которых лежат на одной и
той же прямой, называемой осью
вращения.
143
60
61.
14361
62. ЛЕКЦИЯ № 2 Динамика
14362
63. ВОПРОСЫ 4. Динамика. Масса, инертность, сила. Первый закон Ньютона. 5. Второй закон Ньютона. Третий закон Ньютона. Закон
сохраненияимпульса (вывод). Центр масс (центр
инерции). Закон движения центра
инерции.
6. Реактивное движение. Движение
тел с переменной массой. Уравнение
Мещерского. Формула Циолковского.
143
63
64. Вопрос № 4. Динамика. Границы применимости классического способа описания движения частиц. Масса, инертность, сила.
Фундаментальные силы.Первый закон Ньютона и понятие
инерциальной системы отсчёта.
143
64
65. Динамика изучает движение тел в связи с теми причинами, которые обуславливают тот или иной характер движения. Основная задача
Динамики по силе найтизакон движения или по закону
движения найти силу.
143
65
66. Состояние частиц Абсолютно свободных тел нет. Состояние частицы (и, как следствие, описание её движения) зависит от системы
отсчёта.Например, человек в поезде
покоится относительно вагона и
движется относительно перрона.
Трудно отдать предпочтение той или
иной системе отсчёта.
143
66
67. Законы Ньютоновой механики выполняются если (границы применимости): 1) Пространство Евклидово (т.е. описывается аксиомами
евклидовойгеометрии, также, трёхмерное);
2) Пространство изотропно;
3) Гелиоцентрическая система
инерциальна (в центре системы
солнце, которое движется без
ускорения);
143
67
68. 4) Закон всемирного тяготения выполняется для всей известной для нас вселенной; 5) Изменение всех полей со скоростью света; 6)
Скорость тел много меньшескорости света (v << c);
7) Массы тел много больше масс
элементарных частиц (M >> m).
143
68
69. Основные понятия Масса – физическая величина, мера инертности. Инертность – свойство тел сопротивляться при попытке изменить
скорость.Сила – физическая величина, мера
взаимодействия тел.
143
69
70. В природе существуют четыре фундаментальные силы (все взаимодействия в природе сводятся к этим четырём силам): 1)
Гравитационное взаимодействие(всемирное тяготение);
2) Электромагнитное
взаимодействие (электрическое и
магнитное поле);
143
70
71. 3) Сильное или ядерное взаимодействие (связь частиц в атомном ядре); 4) Слабое взаимодействие (процессы распада элементарных
частиц).143
71
72. 1-й закон Ньютона (закон инерции): Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока
воздействие со стороны других телне заставит его изменить это
состояние.
143
72
73. Инерциальные системы отсчёта – системы отсчёта, в которых тела движутся без ускорения если на них не действуют силы со стороны
других тел или в которыхвыполняется 1-й закон Ньютона.
1-й закон Ньютона нужен для
определения инерциальных систем.
143
73
74.
14374
75. Вопрос № 5. Второй закон Ньютона как уравнение движения. Третий закон Ньютона. Закон сохранения импульса (вывод). Центр масс
(центр инерции). Закондвижения центра инерции.
143
75
76. Законы Ньютона получены в результате обобщения большого количества опытных фактов. Например, в результате взаимодействия
(независимо от видавзаимодействия) два тела получают
ускорения, такие, что выполняется
равенство:
m1a1 m2a2
143
76
77. Если рассматривать через импульс тела – произведение массы тела на его скорость, то получим:
d d m dpm
F ma
dt
dt
dt
143
77
78. Скорость изменения импульса тела равна действующей на тело силе F – уравнение движения тела или основной закон динамики
поступательного движения.Он же 2-й закон Ньютона:
dp
F
dt
143
78
79. 3-й закон Ньютона: Силы с которыми действуют друг на друга взаимодействующие тела, равны по модулю и противоположны по
направлению и направлены вдольлинии, которая проходит через их
центр масс:
F12 F21
143
79
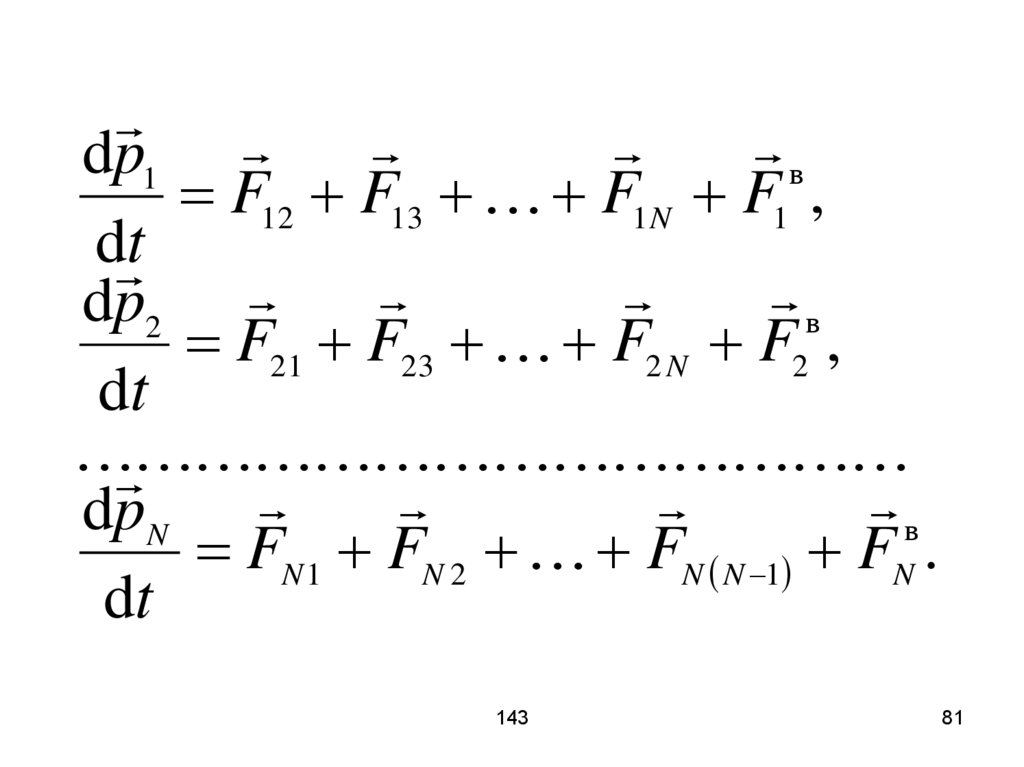
80. Закон сохранения импульса. Рассмотрим замкнутую систему из N тел. Запишем изменение импульса и действующие силы на тело для
каждого тела:143
80
81.
вdp1
F12 F13 F1 N F1 ,
d t
в
dp2
F21 F23 F2 N F2 ,
dt
в
dpN
FN 1 FN 2 FN N 1 FN .
dt
143
81
82. Просуммируем все эти уравнения
NN
N
dpi
в
Fij Fi
i 1 dt
i j
i 1
143
82
83. Первая сумма справа равна нулю по 3-му закону Ньютона: . Втора сумма справа равна нулю так как на замкнутую или изолированную
Первая сумма справа равнанулю
по
3-му закону Ньютона: Fij Fji .
Втора сумма справа равна нулю так
как на замкнутую или изолированную
систему не действуют никакие силы
(внешняя сила равна нулю Fв = 0).
143
83
84. Следовательно Закон сохранения импульса: В замкнутой изолированной системе полный импульс остаётся постоянным.
СледовательноN
N
dpi
dt pi 0 pi const
i 1
i 1
i 1
N
Закон сохранения импульса:
В замкнутой изолированной системе
полный импульс остаётся
постоянным.
143
84
85. Центром масс или центром инерции системы называется такая воображаемая точка, радиус-вектор R которой выражается через
радиусвекторы r1, r2, … материальных точекпо формуле:
m1r1 m2 r2
R
m1 m2
143
85
86. Продифференцируем по времени, умножим на массу всей системы (M = m1 + m2 + …):
MR m1r1 m2 r2 ,MV m1 1 m2 2 ,
p MV .
143
86
87. Отсюда, используя закон сохранения масс, получаем закон движения центра масс: Таким образом, центр масс изменяет своё движение
Отсюда, используя закон сохранениямасс, получаем закон движения
центра масс:
d dp
в
m
F
dt dt
Таким образом, центр масс изменяет
своё движение только под
действием внешней силы.
Внутренние силы на движение
центра масс не влияют.
143
87
88. Примеры: движение снаряда; как до взрыва, так и после взрыва, центр масс движется по параболе, Земля и Луна вращающиеся вокруг
общегоцентра масс, который расположен от
центра Земли на расстоянии 4670
км, при радиусе Земли 6371 км.
143
88
89.
14389
90. 6. Реактивное движение. Движение тел с переменной массой. Уравнение Мещерского. Формула Циолковского.
14390
91. До сих пор рассматривали движение с постоянной массой. Рассмотрим движение с переменной массой – движение ракеты, которая
движетсяза счёт отталкивания от газов,
образовавшихся при сжигании
топлива.
143
91
92. Такое движение принято называть реактивным. Но в широком смысле всякое движение есть реактивное движение, поскольку для
приданияимпульса телу необходимо другое
тело. Между телами происходит
взаимодействие и они могут
двигаться. Без взаимодействия
заставить двигаться тело (или
остановиться) невозможно.
143
92
93. Рассмотрим движение тела с переменной массой – движение ракеты. Пусть m(t) – масса ракеты в момент времени t, ʋ(t) – скорость
ракеты втот же момент, ʋ(t)m(t) – импульс
ракеты.
143
93
94. За время dt масса и скорость получат приращения dm и dʋ (dm < 0, dʋ > 0). Новый импульс ракеты (m + dm) * (ʋ + dʋ), импульс
За время dt масса и скоростьполучат приращения dm и dʋ
(dm < 0, dʋ > 0).
Новый импульс ракеты
(m + dm) * (ʋ + dʋ),
импульс движения газов
dmгаз * ʋгаз.
143
94
95. Изменение импульса за время dt равно приращению Fdt – импульса силы: (m+dm)*(ʋ+dʋ)+dmгаз*ʋгаз – mʋ = Fdt. С учётом того, что
(dm*dʋ)→0mʋ+ʋdm+ mdʋ+dmгаз*ʋгаз – mʋ = Fdt
143
95
96. Далее, изменение массы ракеты со знаком «–»: – dm = + dmгаз; Меняем скорость истечения газа относительно неподвижной системы
отсчёта (относительно Земли) наскорость газа
относительно ракеты ʋотн:
ʋгаз – ʋ = ʋотн:
– ʋотнdm+ mdʋ = Fdt.
143
96
97. Выполняем следующие преобразования: mdʋ = Fdt + ʋотнdm. Делим на дифференциал времени dt и получаем уравнение Мещерского:
14397
98. Запишем уравнение Мещерского – уравнение движения точки с переменной массой
d dm вm
отн
F
dt
dt
143
98
99. Здесь m – масса ракеты, ʋ – скорость ракеты, ʋотн – скорость истечения газов относительно ракеты, dm/dt – скорость сжигания
топлива, Fв – внешняя сила, ʋотнdm/dt – реактивная сила.
143
99
100. Рассмотрим движение ракеты в случае невесомости (Fв = 0). Начальная скорость ракеты равна нулю, направление газов и ракеты
противоположное (ʋ ↑↓ ʋотн):d
dm
dm
m
отн
d отн
dt
dt
m
143
100
101. Решение уравнения Мещерского с этими начальными условиями даёт решение – формулу Циолковского
dmd отн
отн ln m C
m
143
101
102. Константу C определяем из начальных условий: ʋ = 0 – начальная скорость; m0 – начальная масса. C = ʋотнlnm0.
143102
103. Таким образом, получаем формулу Циолковского:
m0exp
.
m
отн
m0
отн ln ,
m
143
103
104.
143104
105. ЛЕКЦИЯ № 3 Законы сохранения
143105
106. ВОПРОСЫ 7. Динамика вращательного движения. Момент импульса частицы. Момент силы. Плечо силы. Уравнение моментов. Закон
сохранения моментаимпульса.
143
106
107. 8. Кинетическая энергия. Работа постоянной и переменной силы. 9. Потенциальная энергия. Условие потенциальности. 10. Закон
сохранения механическойэнергии изолированной системы.
Законы Кеплера.
143
107
108. Вопрос № 7. Динамика вращательного движения. Момент импульса частицы. Момент силы. Плечо силы. Уравнение моментов. Закон
сохранения моментаимпульса.
143
108
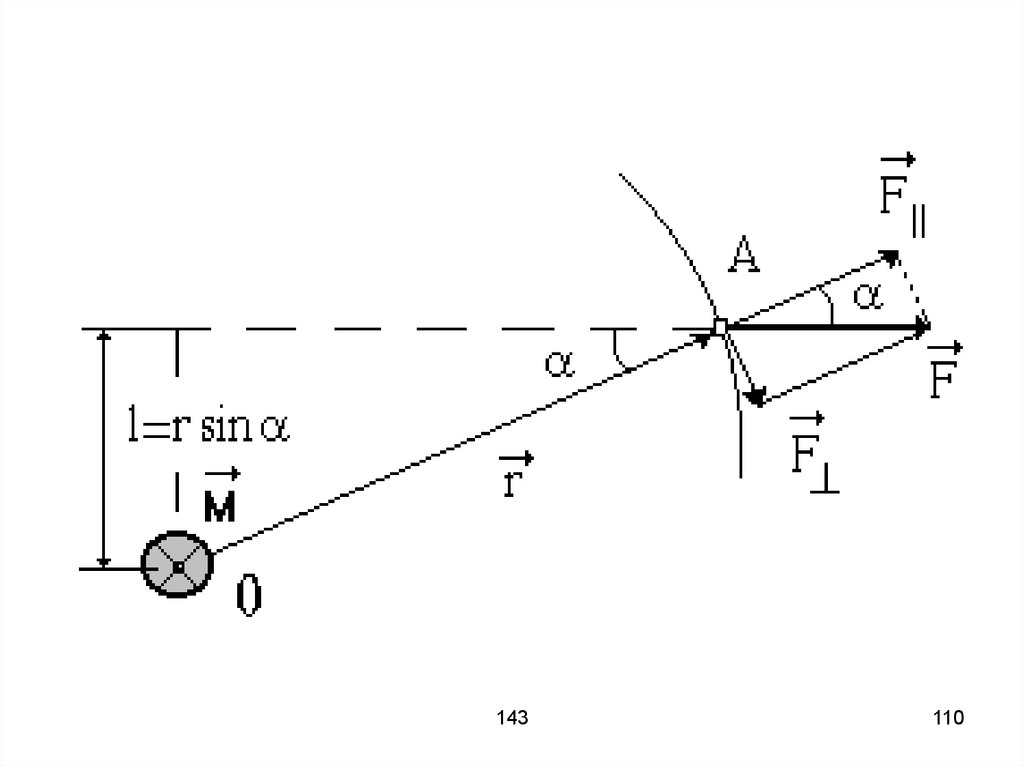
109. Вектором момента силы относительно полюса (точки О) называют векторное произведение радиус-вектора и вектора силы Величина ℓ =
Вектором момента силыотносительно полюса (точки О)
называют векторное произведение
радиус-вектора и вектора силы
M r F
M rF sin α F *
Величина ℓ = r * sinα называется
плечом силы.
143
109
110.
143110
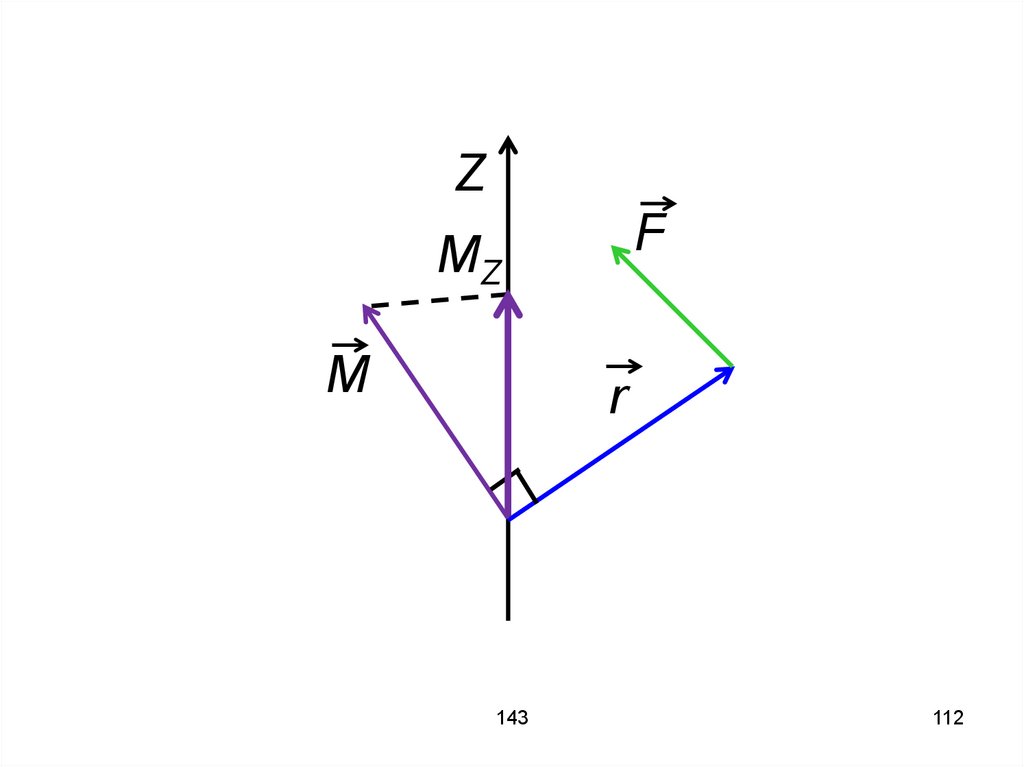
111. Проекция вектора момента силы на произвольную ось, проходящую через полюс, равна проекции на эту ось векторного произведения
радиус-вектора и вектора силыотносительно полюса О, лежащего
на этой оси:
Mz r F
143
z
111
112.
ZF
MZ
M
r
143
112
113. Рассмотрим вопрос следующим способом. Разложим вектор силы F на три составляющие: Fτ, F‖, FR. Fτ – сила перпендикулярная оси Z
иплоскости рисунка;
F‖ – сила параллельная оси Z,
лежащая в плоскости рисунка;
FR – сила перпендикулярная оси Z,
лежащая в плоскости рисунк
143
113
114.
ZF‖
F
R
Fτ
MZ
Mτ
FR
r
143
114
115. Поскольку F‖, FR лежат в плоскости рисунка, то M‖, MR | плоскости рисунка, следовательно, (M‖)z, (MR)z = 0. Fτ | плоскости
рисунка,следовательно, проекция Mτ на ось
Z, не равна нулю ((Mτ)z = 0).
То есть, MZ = (Mτ)z = R· Fτ.
143
115
116. Если на точку действует несколько сил, то можно говорить о равнодействующей силе – векторной сумме сил, действующих на тело
NF F1 F2 FN Fi
i 1
143
116
117. Вектор момента результирующей силы относительно полюса О равен геометрической сумме векторов моментов составляющих сил
относительно того же полюса.N
M M1 M 2 M N M i
i 1
143
117
118. Вектором момента импульса материальной точки относительно полюса О называют векторное произведение радиус-вектора и вектора
импульса относительноэтого же полюса
L r p r mv
L r p rp sin α
143
118
119. Проекция момента импульса твердого тела на произвольную ось, проходящую через полюс О, равна проекции на эту ось векторного
произведения радиус-вектора ивектора импульса тела относительно
того же полюса О, лежащего на этой
оси, т. е.
Lz r p z
143
119
120. Запишем момент импульса и продифференцируем его
L r pL r p r F M
143
120
121. Получили новое выражение, которое называется уравнением моментов или основное уравнение динамики вращательного движения
L M143
121
122. Из основного уравнения динамики вращательного движения Можно получить закон сохранения момента импульса (аналогично закону
Из основного уравнения динамикивращательного движения
L M
Можно получить закон сохранения
момента импульса (аналогично
закону сохранения импульса).
В замкнутой системе (M = 0)
суммарный момент импульса
остаётся
постоянным.
L const
143
122
123. Пространство однородно, следовательно, параллельный перенос системы из одного места в другое не изменяет свойств системы –
закон сохранения импульсанарушаться не будет.
143
123
124. Пространство изотропно, следовательно, поворот замкнутой системы как целого не отражается на её механических свойствах – закон
сохранения момента импульсанарушаться не будет.
143
124
125.
143125
126. Вопрос № 8. Кинетическая энергия. Работа постоянной и переменной силы. Мощность. 1-я и 2-я космические скорости.
143126
127. Запишем уравнение движения частицы и домножим на перемещение (dS = v dt):
m Fвнешd
dt Fвнеш dS
m
dt
2
2
m
m d md d
Fвнеш dS
2 2
143
127
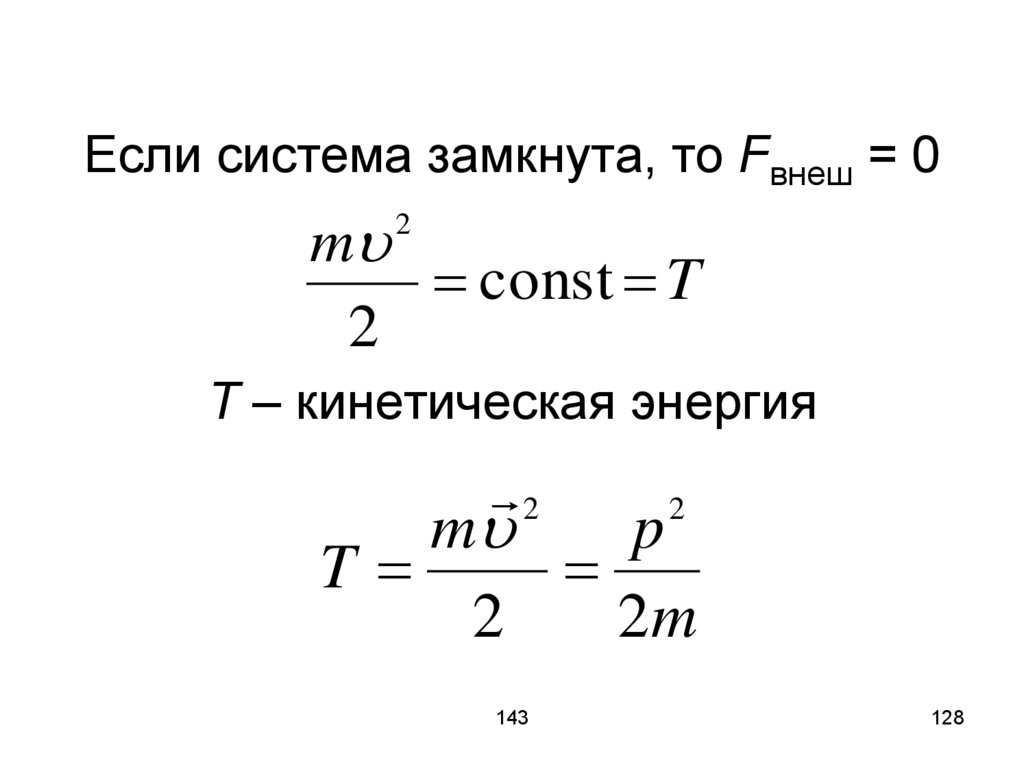
128. Если система замкнута, то Fвнеш = 0 T – кинетическая энергия
Если система замкнута, то Fвнеш = 0m
const T
2
2
T – кинетическая энергия
2
m
p
T
2
2m
143
2
128
129. Если на частицу действует постоянная сила F, кинетическая энергия не остаётся постоянной. В этом случае кинетическая энергия за
время dt изменяетсяна
величину
dA FdS
dA – работа, совершаемая силой F
на пути dS (dS = ʋ*dt). Работа равна
изменению кинетической энергии:
A T2 T1 T
143
129
130. Пример: Вычислим работу, которую совершают внешние силы при сжатии пружины (работа переменной силы): здесь F = kx – внешняя
Пример: Вычислим работу, которуюсовершают внешние силы при
сжатии пружины (работа переменной
силы):
kx
A FdS kxdx
2
1
0
2
x
2 x
0
2
kx
2
здесь F = kx – внешняя сила, равная
силе упругости но противоположно
направленная, k – коэффициент
упругости, x – сжатие пружины.
143
130
131. Мощность – работа совершаемая в единицу времени
dAP
F
dt
143
131
132. Запишем закон всемирного тяготения и потенциальную энергию гравитационного взаимодействия здесь G = 6,6720*10-11 Н*м2/кг2
Запишем закон всемирноготяготения и потенциальную энергию
гравитационного взаимодействия
m1m2
m1m2
F G 2 , W G
,
R
R
здесь G = 6,6720*10-11 Н*м2/кг2
гравитационная постоянная, m1, m2 –
масса тел, R – расстояние между
центрами масс тел.
143
132
133. 1-я космическая скорость – скорость, с которой тело движется над поверхностью земли не падая Скорость тела, которое вращается
1-я космическая скорость – скорость,с которой тело движется над
поверхностью земли не падая
2
M Землиm
M Земли
m G
, G
gR
2
R
R
R
Скорость тела, которое вращается
вокруг Земли на некоторой высоте h
M Çåìëè
v G
R h
143
133
134. Если тело получит достаточное количество энергии (кинетической), то эта энергия будет потрачена на преодоление потенциального
барьера и тело покинет Землюнавсегда. То есть, телу сообщили
2-ю космическую скорость
m
M Землиm
M Земли
G
, 2G
2
R
R
2
143
134
135.
143135
136. Вопрос № 9. Консервативные силы. Потенциальная энергия. Связь силы и потенциальной энергии (условие потенциальности).
143136
137. Взаимодействие между телами осуществляется посредством физических полей. Каждое тело создаёт вокруг себя особое состояние,
называемое силовымполем.
143
137
138. Центральное поле – сила, действующая на любую точку в пространстве направлена к центру. Однородное поле: F = const.
Стационарное поле – поле неменяется со временем.
Нестационарное поле – поле
меняется со временем.
143
138
139. Консервативные силы: 1) Это силы, работа которых не зависит от пути, по которому тело переходит из одного положения в другое;
2) Это силы, работа которых налюбом замкнутом пути равна нулю.
143
139
140. Потенциальная энергия Если работа зависит только от начального и конечного положений, то каждой точке поля можно сопоставить
некоторую функциюU(x, y, z). Величину U назовём
потенциальной энергией.
143
140
141. Через эту функцию можно определить работу по перемещению частицы из 1-го положения во 2-е: A12 = U1 – U2, работа также приводит
к изменениюкинетической энергии:
A = T2 – T1 = U1 – U2 =>
T2 + U2 = T1 + U1 = E –
полная механическая энергия.
Кинетическая энергия увеличивается
за счёт убыли потенциальной.
143
141
142. Зная вид U(x, y, z) можно найти силу, действующую на частицу в каждой точке поля угол α – угол между вектором силы и вектором
Зная вид U(x, y, z) можно найти силу,действующую на частицу в каждой
точке поля
dA FdS FdS cos α
угол α – угол между вектором силы и
вектором перемещения.
В проекции на ось X:
dAx Fx dx dU x
143
142
143. Если полагать, что изменений силы вдоль других осей нет или рассматривать одномерную задачу только вдоль одной оси X (dy, dz =
0;y, z = const), то можно говорить о
частной производной:
dU
U
Fx
dx
x
143
143
144. Если учитывать все компоненты, то получим:
F Fx i Fy j Fz kU U U
i
j
k
x
y
z
U grad U
143
144
145. Здесь grad – это оператор набла или градиент – вектор, направленный в сторону максимального роста поля. Оператор набла –
математическийоператор – компоненты которого
являются частными производными
по координатам
i
j k
y
z
x
143
145
146. Условие потенциальности Поля, которые можно описывать функцией П(x, y, z, t), называются потенциальными, градиент этой функции
определяет силу в каждойточке поля:
F = gradП,
П – потенциал.
143
146
147. В случае стационарного поля, его силы будут консервативными П(x, y, z) = – U(x, y, z).
143147
148.
143148
149. Вопрос № 10. Закон сохранения механической энергии изолированной системы и однородность времени. Обобщённый закон сохранения
энергии.Финитное и инфинитное движение.
Законы Кеплера.
143
149
150. Закон сохранения энергии в механике Полная механическая энергия замкнутой изолированной системы складывается из кинетической
энергии частиц и потенциальнойэнергии взаимодействия частиц:
N
N
i
i j
E Ti U ij const,
Uij – энергия взаимодействия частиц.
143
150
151. Кинетическая энергия поступательного движения Кинетическая энергия вращательного движения
Кинетическая энергияпоступательного движения
m
2
2
Кинетическая энергия
вращательного движения
Iω
2
2
143
151
152. Потенциальная энергия деформированной пружины Потенциальная энергия гравитационного взаимодействия двух тел
Потенциальная энергиядеформированной пружины
kx
2
2
Потенциальная энергия
гравитационного
взаимодействия двух тел
m1m2
G
R
143
152
153. Если в системе есть силы приводящие к потери механической энергии (диссипативные), то полная механическая энергия уменьшается.
Общефизический закон сохраненияэнергии: энергия никогда не
создаётся и не уничтожается, она
может только переходить из одной
формы в другую.
143
153
154. В основе сохранения энергии лежит однородность времени, т.е. равнозначность всех моментов времени. Следовательно, изменение
одного момента времени на другойне изменяет свойств механической
системы. Закон сохранения энергии
выполняется в любой момент
времени.
143
154
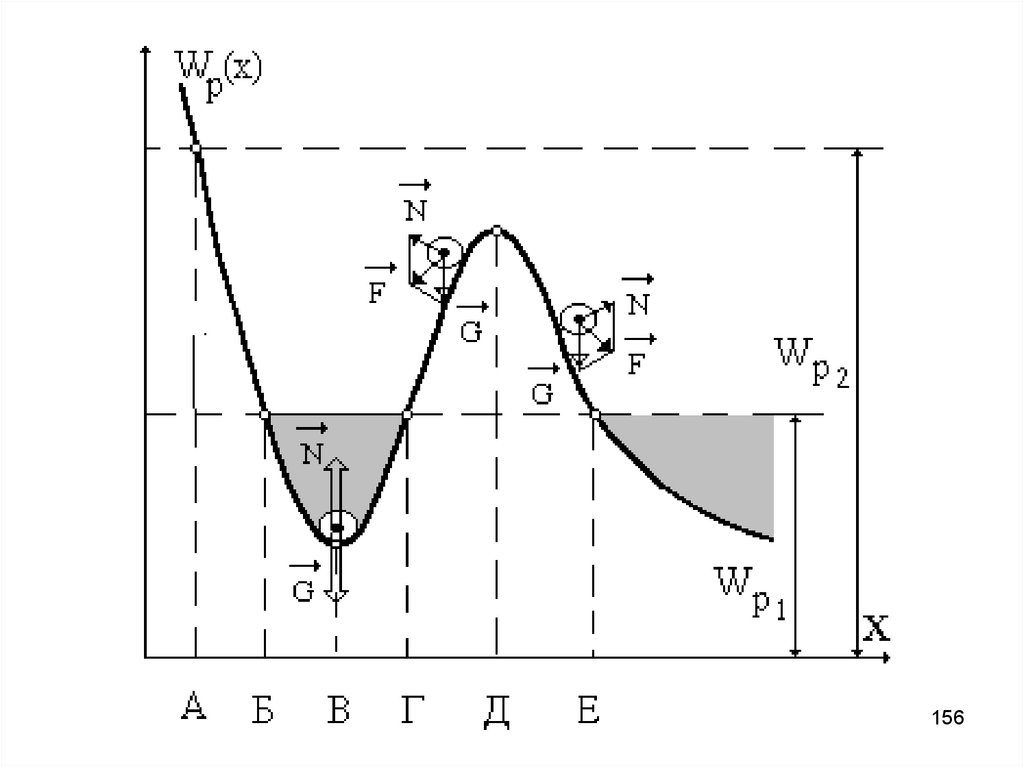
155. Движение частицы в потенциальном поле: Если полная энергия частицы меньше значения потенциального барьера, то частица может
проникать только в ограниченнуюобласть пространства – такое
движение называют финитным. Если
частица может преодолеть
потенциальный барьер, то движение
будет инфинитным
(неограниченным).
143
155
156.
143156
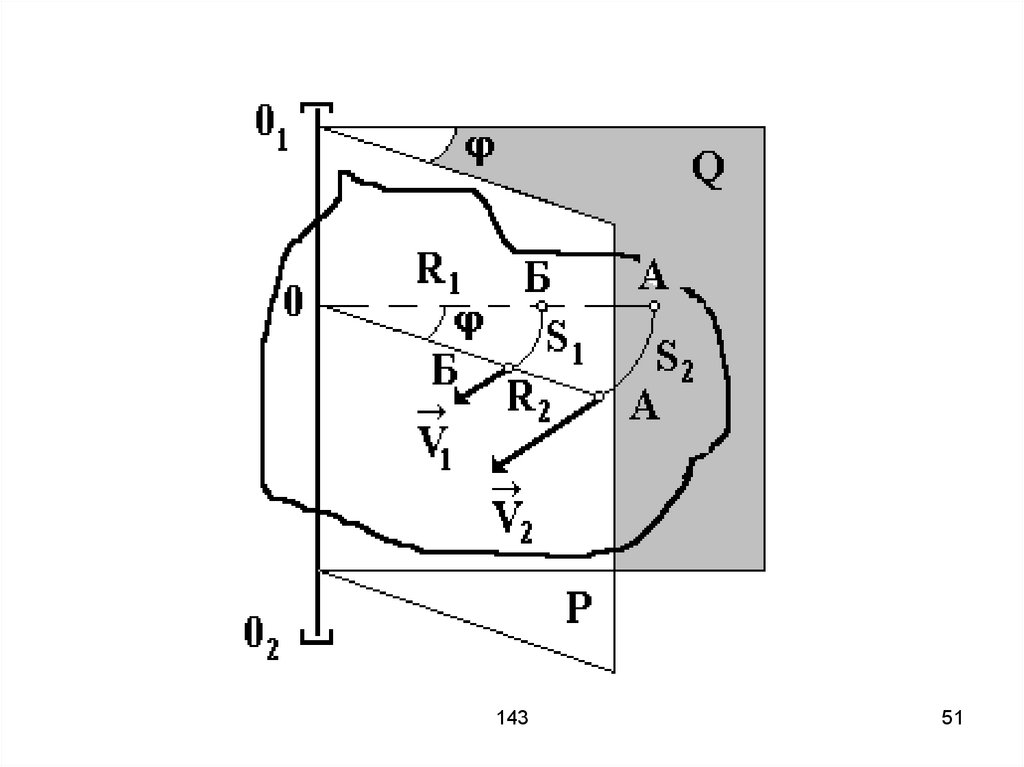
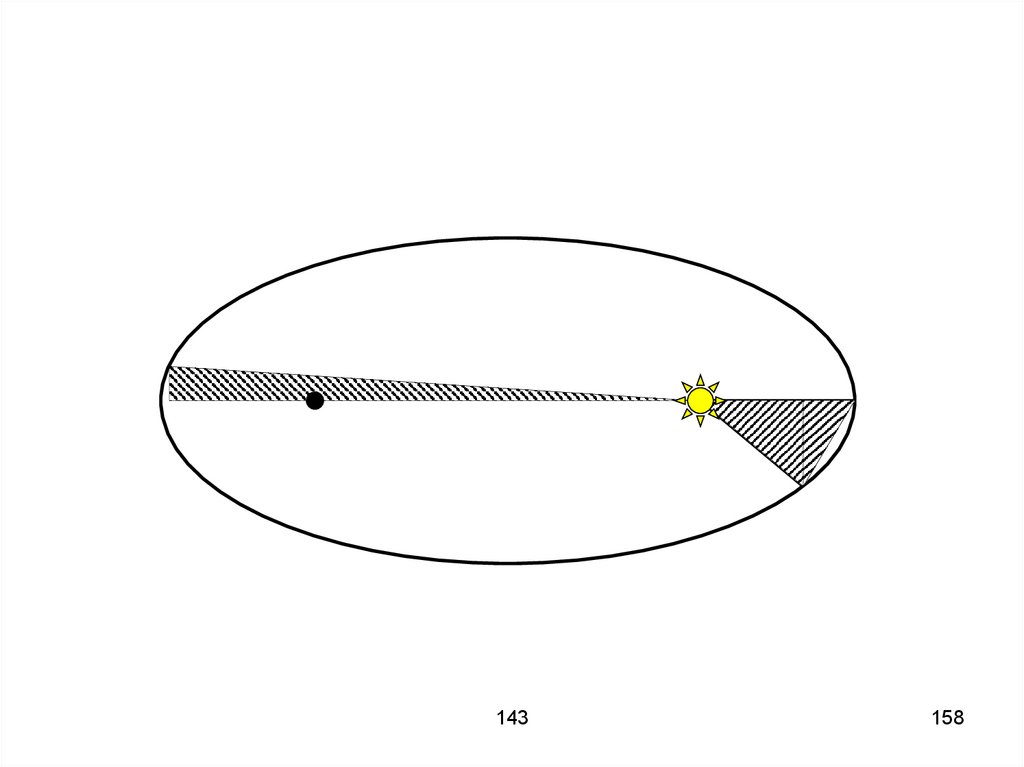
157. Законы Кеплера 1) Каждая планета движется по эллипсу, в одном из фокусов которого расположено Солнце. 2) Радиус-вектор планеты
в равныепромежутки времени описывает
равные площади.
143
157
158.
143158
159. 3) Квадраты периодов обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг
Солнца.2
T1
2
T2
143
3
R1
3
R2
159
160. На основе законов Кеплера Ньютон открыл закон всемирного тяготения здесь G = 6,6720*10-11 Н*м2/кг2 гравитационная постоянная,
На основе законов Кеплера Ньютоноткрыл закон всемирного тяготения
m1m2
F G 2
R
здесь G = 6,6720*10-11 Н*м2/кг2
гравитационная постоянная, m1, m2 –
масса тел, R – расстояние между
центрами масс тел.
143
160
161. Абсолютно упругий удар – удар, при котором механическая энергия тел не переходит в другие виды энергии, тела после удара
продолжаютдвигаться раздельно.
Абсолютно неупругий удар – удар,
после которого тела движутся
совместно с одинаковой скоростью,
либо покоятся.
200
161
162. Закон сохранения импульса выполняется в обоих случаях. Закон сохранения энергии выполняется в случае абсолютно упругого удара.
В случае абсолютно неупругогоудара закон сохранения
механической энергии не
выполняется. Механическая энергия
полностью или частично переходит в
немеханические виды энергии.
200
162
163. Рассмотрим абсолютно неупругий удар двух шаров массами m1 и m2. Удар будем считать центральным – скорости шаров направлены
вдольлинии, которая проходит через их
центры масс. Закон сохранения
импульса будет выглядеть так
m1V10 m2V20 m1 m2 V
V10, V20, V – скорость шаров до и
после удара.
200
163
164. m1 V10 V20 m2, V
200164
165. Рассмотрим абсолютно упругий центральный удар. В этом случае необходимо записать закон сохранения энергии и закон сохранения
механическойэнергии
m1V10 m2V20 m1V1 m2V2
2
2
2
2
m1V10 m2V20 m1V1 m2V2
2
2
2
2
200
165
166. m1 V10 V20 m2, V1 V2
200166
167. Решив совместно эти уравнения получим выражения для скорости шаров после удара
m1V10 m2V20V1 V10 2
,
m
m
1
2
m1V10 m2V20
V2 V20 2
.
m1 m2
200
167
168. Отметим, что если масса одно шара много больше второго, то его скорость изменяться практически не будет, скорость второго
изменитсязначительно (первое уравнение для
случая m1 << m2, второе для случая
m1 >> m2)
V1 V10 2V20 ,
V2 V20 2V10 .
200
168
169. Если при столкновении шаров один из них покоится и их массы равны, то ударяющий после удара будет покоиться, а другой продолжит
движение со скоростью первогошара.
200
169
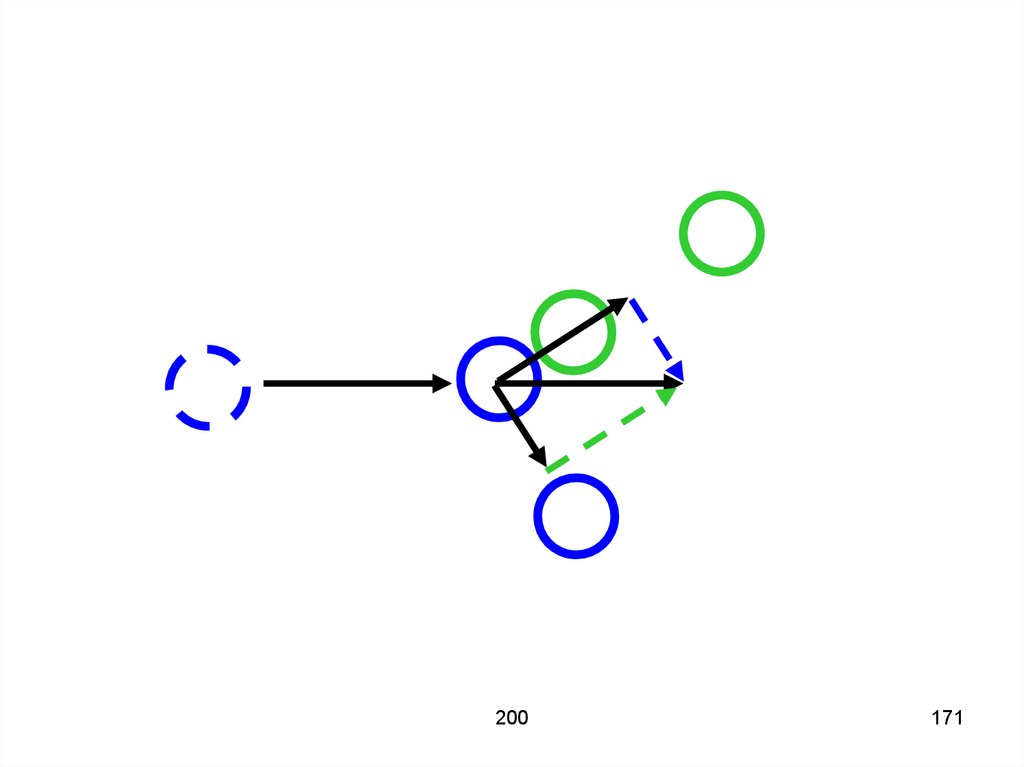
170. Если при столкновении шаров один из них покоится и их массы равны, а удар не центральный, то после удара шары будут двигаться
так, чтоугол межу их векторами будет равен
90°.
200
170
171.
200171
172.
143172










































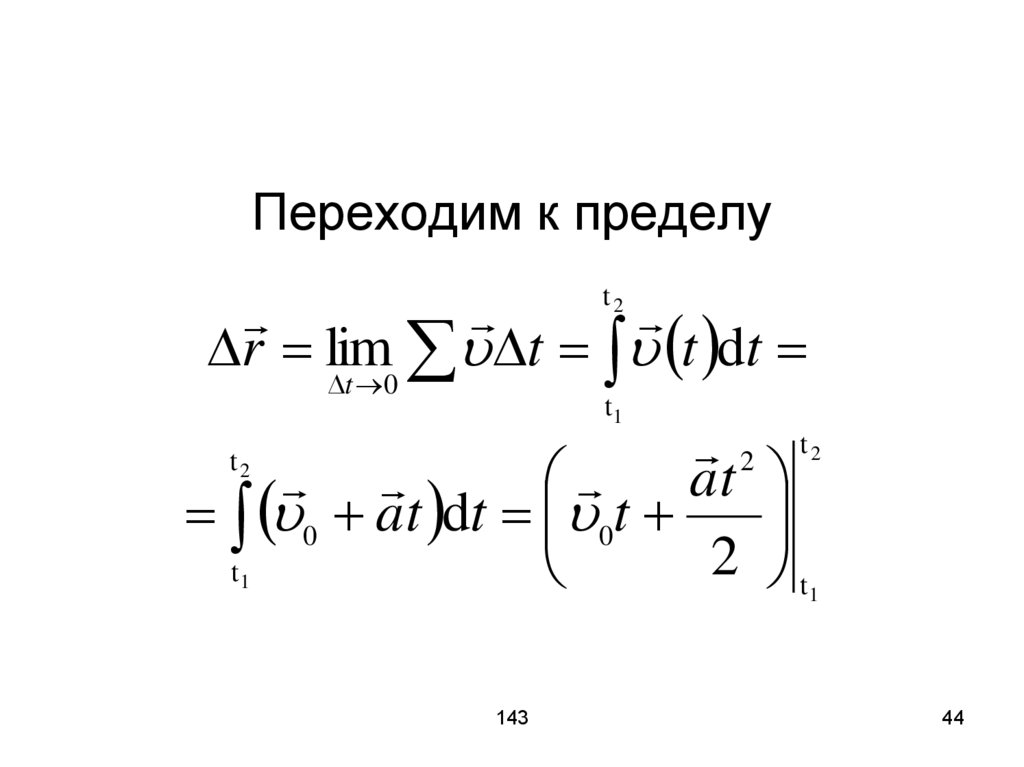























































































































 Физика
Физика








